基于逻辑Petri网的循环选择驱动循环结构过程模型修复方法

刘 伟,薄玉娟,杜玉越,孙红伟

(山东科技大学 计算机科学与工程学院,山东 青岛 266590)

如今多数企业使用信息系统管理业务流程,而过程挖掘主要从信息系统中抽取信息[1]。过程挖掘可分为过程发现、一致性检查和过程增强等阶段[2]。过程发现通过算法从事件日志中挖掘模型;一致性检查是将日志与模型进行比对[3-4],若出现偏差说明过程模型不能反映现实,需要对过程模型进行修复;过程增强使用现有事件日志对原始模型进行改进或扩展,以适应更多事件日志。

现有模型修复方法主要使用校准获得偏差[5]。比如,最具代表性的Fahland方法[6]根据过程发现算法挖掘子过程,修复后的模型无限次重复子过程,然而这种子过程通常不允许重复;Knapsack方法[7]通过设置模型移动和日志移动成本,比较多种不同方案得到最小总成本,获得最佳模型修复方法,但该方法修复的模型包含不可见变迁。这两种方法修复的过程模型虽然提高拟合度,但不能保证模型的简洁度,不能获得很好的修复效果。文献[8]基于Petri网的过程模型修复方法,针对循环结构和选择结构,提出模型偏差域识别方法, 该方法虽然保证了简洁度,但没有考虑各结构间的逻辑关系。为了解决该问题,基于逻辑Petri网,文献[9]提出构造自由循环结构过程模型的修复方法,可根据事件日志识别有问题的变迁构造循环结构。

现有模型修复方法很少考虑包含间接依赖关系的过程模型。如含循环选择驱动循环结构的过程模型,由两个循环块和一个选择块组成,第二个循环体的循环次数取决于第一个循环体的循环次数和执行的选择分支[10]。随着业务流程愈加复杂,流程出现了各种特殊事件日志,如第一个循环块没有执行完就执行选择块,选择分支混合执行,间接依赖关系发生改变等。现有修复方法通过添加不可见变迁或自循环修复模型,但简洁度不高,修复结果不能满足要求。因此,本研究针对循环选择驱动循环结构,提出一种基于逻辑Petri网的过程模型修复方法。首先,针对循环选择驱动循环结构,提出从事件日志中提取循环子日志和选择子日志的算法,判断模型中的循环结构和选择结构;其次,提出两个定理用于发现事件日志和原始模型中关于循环和选择结构的偏差,找到偏差位置并提出修复算法进行模型修复;然后,引入关联规则表达不同结构间的间接依赖关系;最后,对建筑公司工程项目过程进行模拟实验,验证提出方法的合理性和可行性。

1 基本概念

首先介绍一些基本概念,包括迹和事件日志、Petri网、过程模型、逻辑Petri网等。

定义1(迹和事件日志)[11]A是一个活动集合,A*表示集合A上所有有限序列,B(A*)表示集合A上的多集集合,σ∈A*为一个迹,L∈B(A*)为一个事件日志。

定义2(前驱与后继)[11]σ∈A*为一个迹,活动a∈σ,且在σ中a的位置为i,#a是a的前驱,在σ中的位置为i-1;a#是a的后继,在σ中的位置为i+1。

定义3(Petri网)[12-14]PN=(P,T;F,M)为一个Petri网,当且仅当:

1)N=(P,T;F)为一个网,P为库所集,T为变迁集;

2)F⊆(P×T)∪(T×P)表示有向连接弧集合;

3)M:P→N为一个标识。

定义4(前集和后集)[14]PN=(P,T;F,M)为一个Petri网,•x={y∈P∪T∧(y,x)∈F}为x的前集,x•={y∈P∪T∧(x,y)∈F}为x的后集。

定义5(过程模型)[15]Ns=(PN,a,Mi,Mf)为一个过程模型,其中:

1)PN=(P,T;F,M)为一个Petri网;

2)a:T→A∪{τ}是变迁到活动的映射函数,τ为不可见变迁;

3)mi=[pi]∈Mi是初始标识,mf=[po]∈Mf是终止标识。

图1为一个基于Petri网的过程模型实例。

图1 基于Petri网的过程模型实例

定义6(过程树)[16]A为活动集合,⊕={→,×,∧,}为操作符集合,τ为不可见变迁,其中:

1)a∈A∪{τ}为一棵过程树;

2) 若PT1,PT2,…,PTn为n棵过程树,则⊕(PT1,PT2,…,PTn)也是一棵过程树,→表示顺序关系,×表示选择关系,∧表示并发关系,表示循环关系。

图1过程模型可表示为过程树PT1:→(a,(b,c),d,×(→(e,g),→(f,h)))。

定义7(逻辑Petri网)[17]LPN=(P,T;F,I,O,M)为一个逻辑Petri网,其中:

1)P是有限库所集;

2)T=TI∪TO∪TD是有限变迁集,P∪T≠Ø,P∩T=Ø;若t∈TI∪TO,•t∩t•=Ø;其中,TI为逻辑输入变迁集,TO为逻辑输出变迁集,TD为经典Petri网变迁集;

3)F⊆(P×T)∪(T×P)为有向连接弧集合;

4)I是从逻辑输入变迁到逻辑输入函数的映射,对∀t∈TI,I(t)=fI(t);

5)O是从逻辑输出变迁到逻辑输出函数的映射,对∀t∈TO,O(t)=fO(t);

6)M:P→N为一个标识函数。

2 循环选择及其驱动循环序列确定算法

本部分介绍循环选择驱动循环结构,并划分为循环结构和选择结构分别进行分析。图2为一个循环选择驱动循环结构过程模型,使用关联规则表示不同结构之间的间接依赖关系,比如关联规则〈b,c〉2∧〈e,g〉1⟹〈j,k〉1表示循环活动b、c发生两次后执行e、g选择分支,则第二个循环块执行一次循环。

图2 循环选择驱动循环结构过程模型

2.1 循环序列确定算法

对循环选择驱动循环结构进行修复,首先要找到模型中所有循环结构。假设每个过程模型都有一个唯一的过程树,过程树中每个操作符代表模型的一个结构。例如在模型中有一个循环结构,则相应过程树节点n=“”。为方便起见,Fi(n)表示n节点处第i个子树的所有叶节点。

定义8(活动发生次数) σ∈L为日志中的一个迹,s∈σ为一个序列,对于任意活动a∈σ,num(a,σ)表示活动a在迹中出现的次数,num(s,σ)表示序列s在迹中出现的次数。

定义9(循环活动) σ∈L为日志中的迹,a∈σ为一个活动,若num(a,σ)>1,则a为循环活动。

循环活动集合SLA={a∈σ|∃σ∈L∧num(a,σ)>1}。

定义10(活动集)A为活动集合,对任意序列s∈A*,κ(s)为序列s中的活动集。

定义11(循环序列)SLA为循环活动集合,s=〈s[1],s[2],…,s[i],…,s[n]〉∈SLA*为一个循环序列,其中s[i]∈SLA,i∈{1,2,…,n-1}。以|s|表示序列s的长度。若:

1)κ(s)=1,s为自循环序列;

2)κ(s)=2,且s[1]>Ls[2],s为短循环序列,|s|=2;

3)κ(s)>2,且s[i]>Ls[i+1],|s|-2>i>0,s为长循环序列。

Ls为所有循环序列集合。

定义12(循环开始活动和循环结束活动)SLA为循环活动集合,s∈SLA*为一个循环序列,循环开始活动为SLA_s,循环结束活动为SLA_e,其中:

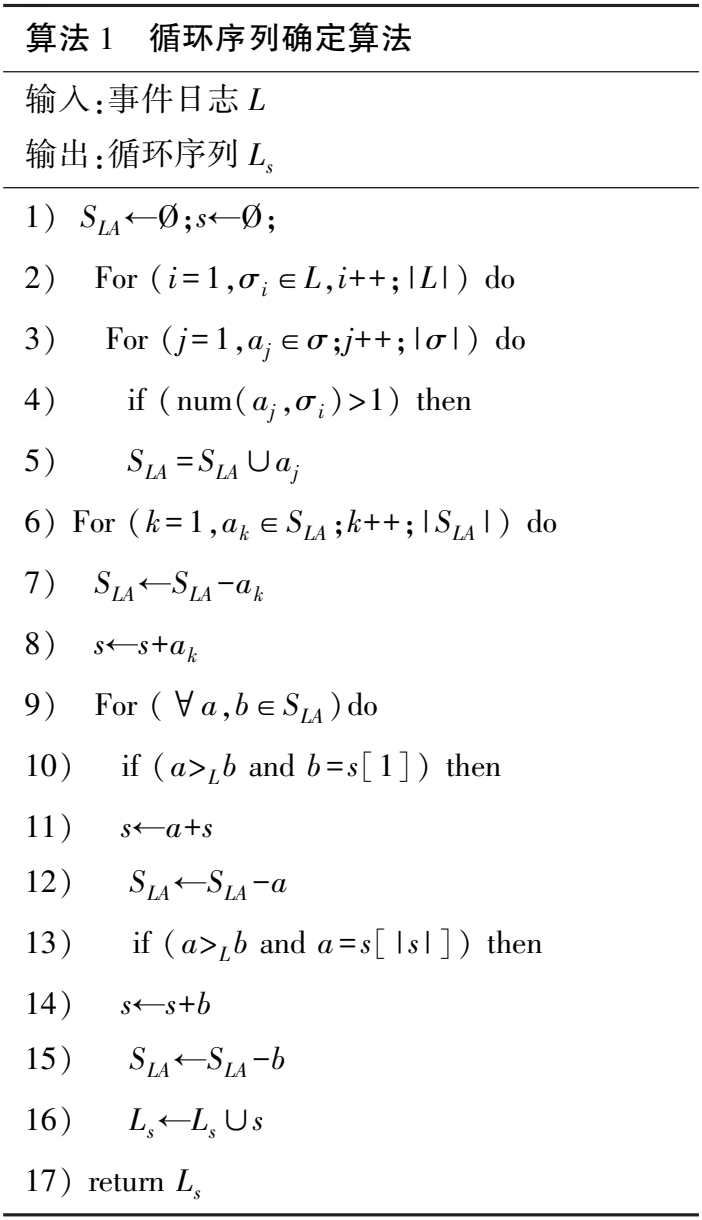
算法 1 循环序列确定算法 输入:事件日志 L 输出:循环序列 Ls 1) SLA←Ø;s←Ø; 2) For (i = 1,σi∈L,i++; | L | ) do 3) For (j = 1,aj∈σ;j++; | σ| ) do 4) if (num(aj,σi) >1) then 5) SLA = SLA∪aj 6) For (k = 1,ak∈SLA ;k++; | SLA | ) do 7) SLA←SLA -ak 8) s←s+ak 9) For (∀a,b∈SLA )do 10) if (a>L b and b = s[1]) then 11) s←a+s 12) SLA←SLA -a 13) if (a>L b and a = s[ | s| ]) then 14) s←s+b 15) SLA←SLA -b 16) Ls←Ls∪s 17) return Ls

1)SLA_s=(ai∈SLA|ai=si[1]);

2)SLA_e=(ai∈SLA|ai=si[n]),i∈{1,2,…,m}。

算法1为循环序列确定算法。步骤1)初始化循环序列;步骤2)、3)遍历日志和迹;步骤4)～5)表明若迹σi中的活动aj出现次数>1,则活动aj为循环活动;步骤6)～8)遍历循环活动集合,添加循环活动到循环序列s中;步骤9)～12)表示若循环活动a,b为顺序关系且活动b为s的第一个活动,把活动a添加到s中且在活动b之前;步骤13)～15)表示若循环活动a,b为顺序关系且活动a为s的最后一个活动,则把活动b添加到s中且在活动a之后;步骤16)、17)把得到的循环序列s添加到循环序列集合Ls中并返回Ls。

例1L={〈a,b,c,g〉,〈a,b,c,d,e,g〉,〈a,b,c,d,e,b,c,d,e,g〉}。num(b,σ3)=2,num(c,σ3)=2,num(d,σ3)=2,num(e,σ3)=2,所以SLA={b,c,d,e}。根据算法1,SLA=SLA-b={c,d,e},s=〈b〉,因为b>Lc,有s=s+c=〈b,c〉,SLA=SLA-c={d,e},同理得到s=〈b,c,d,e〉。

2.2 选择序列确定算法

提取出事件日志中的循环序列后,下一步确定事件日志中的选择序列。

定义13(选择活动) σ1,σ2∈L为日志中的两个迹,a∈σ为迹中的一个活动,若a∈σ1,a∉σ2且a∉SLA,则a为选择活动。选择活动集合SCA={a∈A|∃σ1,σ2∈L∧a∈σ1∧a∉2∧a∉SLA}。

定义14(选择序列)SCA为选择活动集合,f∈SCA*为一个选择序列,其中∀f[i]∈SCA,若:

1)κ(f)=1,f为只包含一个活动的选择序列;

2)κ(f)≥2,且f[i] >Lf[i+1],i∈{1,2,…,n-1},f为长度为n的选择序列;

Lf为所有选择序列集合。

定义15(选择开始活动和选择结束活动)SCA为选择活动集合,f∈SCA*为一个选择序列,选择开始活动为SCA_s,选择结束活动为SCA_e,其中:

1)SCA_s=(ai∈SCA|ai=fi[1]);

2)SCA_e=(ai∈SCA|ai=fi[n]),i∈{1,2,…,m}.

定义16(选择分支)Ns=(PN,a,Mi,Mf)为一个过程模型,PT为对应过程树,CB=(t1,t2,…,tn)是一个选择分支元组,其中:

1) ∃n=“×”∈PT;

2)tk∈Fi(n),1≤k≤m,1≤i≤n。

选择分支集合SCB={(t1,t2,…,tn)|tk∈Fi(n),1≤k≤m,1≤i≤n,∀n=“×”∈PT}。

算法2为选择序列确定算法。步骤1)初始化选择序列f,选择活动集合SCA;步骤2)遍历日志;步骤3)～4)表明若活动a属于L,但不属于迹σi,则a为选择活动;步骤5)～9)遍历SCA,若活动a,b为顺序关系且a不属于SCA,b是选择活动,则添加b到f;步骤10)～12)表示若活动a,b为顺序关系且a属于SCA,b不是选择活动,则添加a到f;步骤13)～14)把f添加到选择序列集合Lf中并返回Lf。

例2事件日志L={σ1,σ2}={〈a,b,d,f〉,〈a,c,e,f〉},选择活动集合SCA={b,c,d,e}。对于σ1,有a>Lb且b∈SCA,a∉SCA。根据算法2,f=〈b〉,SCA={c,d,e},d>Lf且d∈SCA,f∉SCA,选择序列f=〈b,d〉,SCA={c,e}。同理可得选择序列集合Lf={〈b,d〉,〈c,e〉}。

算法 2 选择序列确定算法 输入:事件日志 输出:选择序列 Lf 1) SCA ← Ø,f ← Ø; 2) For (i = 1,σi ∈ L;i + +; L ) do 3) if a ∈ L ∧ a ∉σi then 4) SCA ←SCA ∪ a 5) For (i = 0;i < | SCA | ;i + +) do 6) For ∀a,b ∈ A do 7) if (a > L b ∧ a ∉SCA ∧ b ∈SCA ) then 8) f ← f + b 9) SCA ←SCA - b 10) if (a > L b ∧ a ∈SCA ∧ b ∉SCA ) then 11) f ← f + a 12) SCA ←SCA - a 13) Lf ←Lf ∪ f 14) return Lf

2.3 循环选择驱动循环序列确定算法

定义17(切分子迹) σ=〈r1,s,r2,…,rn〉∈L为日志上的一个迹,del(s,σ)={〈r1〉,〈r2,…,rn〉}。

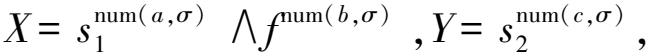
算法3为循环选择驱动循环序列确定算法。步骤1)初始化关联对集合Aϖs,循环选择驱动循环序列Llc→l;步骤2)、3)遍历事件日志和循环序列集合;步骤4)～7)表明若有循环序列sj属于σi,活动a属于sj,且a是循环结束活动,记录a出现次数,同时切分子迹σi为λ1;步骤8)遍历选择序列集合;步骤9)～12)表明若有选择序列fk属于λ1[2],活动b属于fk,且b是选择开始活动,记录b出现次数,同时切分子迹λ1[2]为λ2;步骤13)遍历循环序列集合;步骤14)～16)表明若有循环序列sm属于λ2[2],活动c属于sm,且c是循环结束活动,记录c出现次数;步骤17)、18)得到Aϖs;步骤19)、20)得到并返回Llc→l。

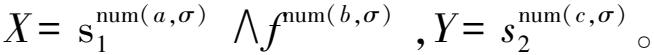
3 循环选择驱动循环结构过程模型修复方法

对于循环选择驱动循环结构,不同循环次数和选择分支执行会影响第二个循环块的执行。在实际过程中,可能会发生循环结构没有执行完就执行选择结构、选择块的选择分支交叉执行等情况。此时迹中没有包含完整循环活动,或迹中选择活动来自不同的选择分支。本节给出含循环选择驱动循环结构过程模型修复算法,在确定过程模型中的偏差位置后,对循环选择驱动循环结构进行修复。

3.1 偏差位置确定算法

本研究将循环选择驱动循环结构分为不同结构分别确定偏差位置。步骤为:①判断循环结构是否存在偏差。若某循环结构不存在循环前进路径[1]、循环活动出现次数不同且出现次数大于1,则确定循环结构存在偏差;②判断选择结构是否存在偏差。若某迹中选择活动来自不同的选择分支,说明选择结构存在偏差;③通过关联规则判定原过程模型的间接依赖关系是否正确,若存在错误,则利用关联规则进行改进。

定理1若a∈SLA是一个没有循环前进路径的循环结构中的循环活动,且存在某个迹有num(a,σ)>num(a#,σ)>1,则偏差位置在循环结构且a为偏差变迁。

证明：循环活动a有num(a,σ)>1,即在某迹中出现次数大于1,说明循环体执行了多次,同时num(a, σ)>num(a#,σ),a的出现次数大于a的后继变迁出现次数,说明a执行完后没有执行a#,循环体没有执行完,确定循环结构存在偏差。

定理2a、b∈SCA为两个选择活动,且a、b属于不同的选择分支,若存在某个迹同时含有a、b两个选择活动,则选择结构含有偏差,偏差变迁为a、b。

算法 4 偏差变迁确定算法 输入:事件日志,循环活动 SLA ,选择活动 SC A ; 输出:偏差变迁 Dt l,Dt c . 1) Dt l,Dt c ← Ø 2) For (i = 1,σi ∈ L;i + +;i ≤| L | ) do 3) if (a,a # ∈SLA ∧ num(a,σ) > num(a # ,σ) > 1) then 4) Dt l ← a 5) if (b,c ∈SCA ∧ b ∈SCBi ∧ c ∈SCBj) then 6) Dt c ← b,c 7) return Dt l,Dt c

证明：a、b∈SCA为两个选择活动,且a、b选择分支不同,说明a和b不能同时出现在一个迹中,因为选择结构的每次执行只会执行一个选择分支,若存在某个迹同时含有a、b两个选择活动,说明a、b所属的选择分支同时混合执行,确定选择结构含有偏差。

算法4为偏差变迁确定算法。步骤1)初始化偏差变迁Dtl、Dtc;步骤2)遍历日志;步骤3)～4)表明若活动a,a#属于循环活动SLA,并且a在迹中出现次数大于a#在迹中出现次数大于1,则a为循环偏差变迁;步骤5)～6)表明若活动b、c属于选择活动SCA,b和c属于不同选择分支,则b、c为选择偏差变迁;步骤7)返回偏差变迁。

3.2 循环选择驱动循环结构过程模型修复方法

算法5为循环选择驱动循环结构过程模型修复算法。步骤1)初始化LPN′;步骤2)根据算法4找到偏差变迁Dtl,Dtc;步骤3)～9)表明若存在循环偏差变迁Dtk,遍历Dtl,确定偏差位置DP=(ti,po),其中ti=Dtk,po=•Dtk;步骤10)～16)表明若存在选择偏差变迁Dti和Dtj,同时Dti不是选择结束活动,Dtj不是选择开始活动,确定偏差位置DP=(ti,po),其中ti=Dti,po=•Dtj;步骤17)返回LPN′。

例3L1={σ1,σ2,σ3,σ4}={〈a,b,c,d,e,g,j,l〉, 〈a,b,c,b,c,b,d,e,h,i,j,k,j,k,j,k,j,l〉, 〈a,b,c,b,c,d,e,g,i,j,k,j,l〉〈a,b,c,b,c,b,c,d,f,h,i,j,k,j,k,j,l〉}。在过程模型NS2中,循环活动为{b,c,j,k},选择活动为{e,f,g,h}。对于迹σ2,包含活动b和c的循环块中b的发生次数比c的发生次数多并且两个活动发生了多次,说明循环结构发生偏差。根据算法4确定偏差变迁为b,b的前集库所为p2,根据算法5确定偏差位置DP=(b,p2)。添加一条从偏差变迁b到前集库所p2的弧,修改b为逻辑输出变迁,O(b)=p2⊗p3。迹σ2中的选择活动来自两个不同的选择分支,根据算法4确定偏差变迁为e和h,e的后集库所为p5,h的前集库所为p6。因为h为选择结束活动,根据算法5确定偏差位置DP=(e,p6), 添加一条从偏差变迁e到前集库所p6的弧,修改e为逻辑输出变迁,O(e)=p5⊗p6,得到图3。Fahland方法添加了一个重复变迁,两个不可见变迁和六条弧重放L1中的迹,如图4。相对于只添加了两条弧的图3,Fahland方法比较复杂,并且不能表示过程模型不同结构间的间接依赖关系。

图3 基于逻辑Petri网的过程模型修复方法修复的模型

4 模拟实验

本研究选用Fahland方法进行对比实验,评估提出方法的正确性和有效性。基于逻辑Petri网的模型修复采用手工模拟方式,Fahland方法已在过程挖掘工具Prom6.6(http://www.promtools.org/prom6/)中实现。

4.1 实验数据与模型

以建筑公司工程项目实施过程为例,如图5所示。建筑公司首先投标,中标后监理单位对施工方案进行专业评审,如果评审不通过需要对施工方案进行修改,重新确定施工方案。确定方案后需要准备施工材料,建筑公司有两种方案选择材料公司:竞争性谈判或者招标,谈判可直接确定材料公司并确定材料,招标则要实地考察材料后才能确定材料。确定施工材料后要对材料送检后施工,施工时要定期质检,最后完成工程项目。通过算法3可以发现日志中存在间接依赖关系,比如在修改方案、确定方案发生一次后,选择竞争性谈判确定材料公司可以使施工质检阶段执行3次等,故可以确定此模型为含循环选择驱动循环结构过程模型。

图5 建筑公司工程项目实施过程模型

实际过程可能会出现一些情况:对施工方案进行修改,修改完成后不需要再进行评审、经过竞争性谈判选择的材料公司依旧需要实地考察等。此时原始模型不能满足这些情况,需要修复模型。从某建筑公司系统中获取10组事件日志L1～L10,如表1所示(可以通过链接https://www.aliyundrive.com/s/BWaeSsq1zQv获取)。本研究基于这10组事件日志进行模型修复。

表1 事件日志信息

4.2 模型修复实验

通过与Fahland方法对比,验证本研究方法的合理性和正确性。图6为利用Fahland方法修复后的模型,比图5增加了1个重复变迁、2个不可见变迁和6条流关系。基于逻辑Petri网的修复方法如图7所示,比图5增加了2条弧和2个逻辑函数,同时根据关联规则添加了新的间接依赖关系。

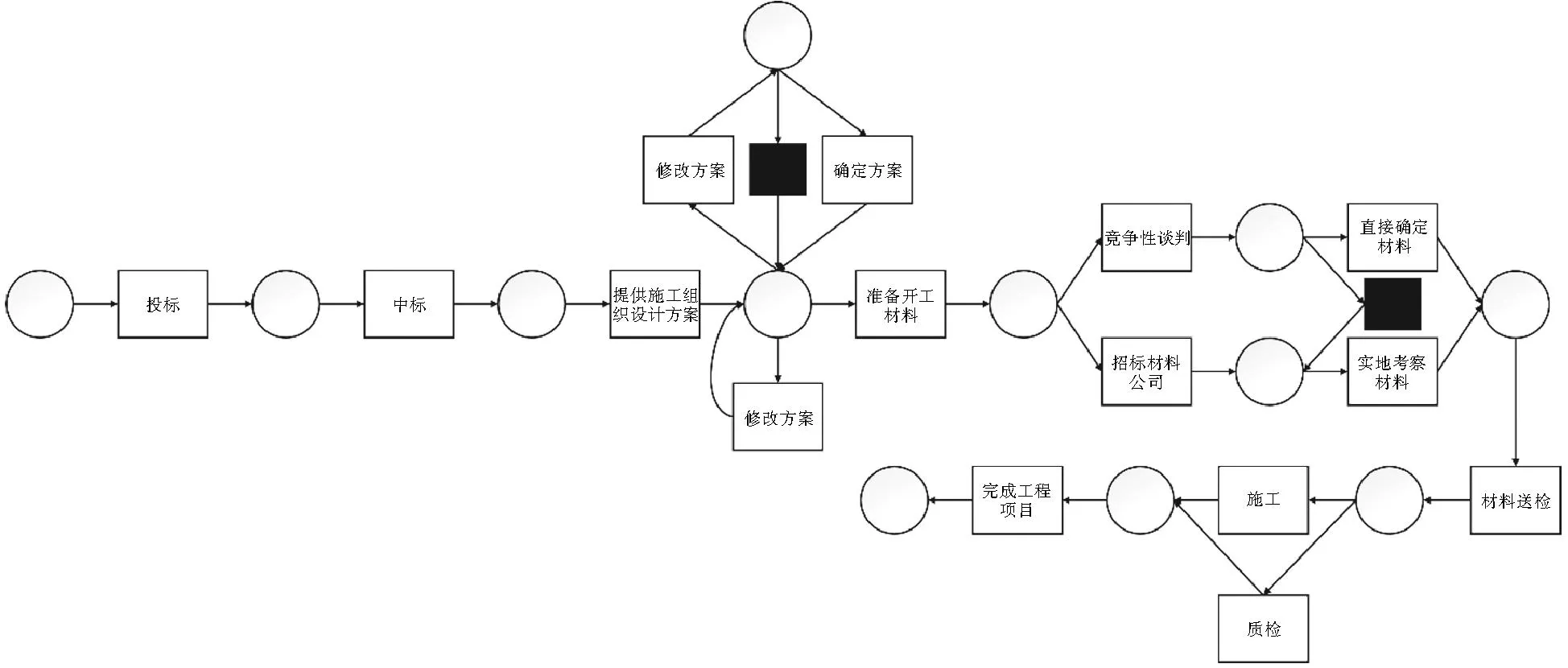
图6 基于Fahland方法修复的模型

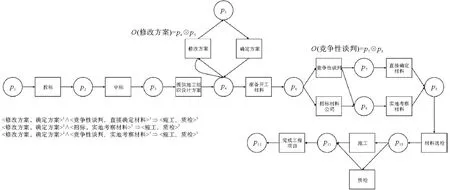
图7 基于逻辑Petri网的过程模型修复方法修复的模型

4.3 模型分析

本节从拟合度、精确度、简洁度三方面对两种修复方法得到的模型进行分析。拟合度用于确保事件日志中行为的发生,模型的拟合度越高,说明模型重复事件日志的能力越强,模型的质量越好;精确度是指过程模型不会发生除事件日志外其他行为的能力,模型的精确度越高,模型生成外部事件日志的迹就越少,模型的质量也越好;简洁度是用简单的模型重演日志中所有迹的能力,简洁度太低会影响模型的可读性。逻辑Petri网模型拟合度、精确度的计算方法见文献[18]。

不同日志情况下,两种方法修复的模型拟合度、精确度分别如图8、图9所示。相较于Fahland方法,本研究方法修复后模型的拟合度、精确度更高,修复效果更好。Fahland 方法在修复过程模型时增加了自循环,导致过程模型产生许多事件日志之外的迹,使得修复后的模型拟合度、精确度降低。本研究基于逻辑Petri网,针对循环选择驱动循环结构,提出修复方法,在修复循环选择驱动循环结构的同时可以表达结构间的间接依赖关系,提高了修复后模型的拟合度和精确度。

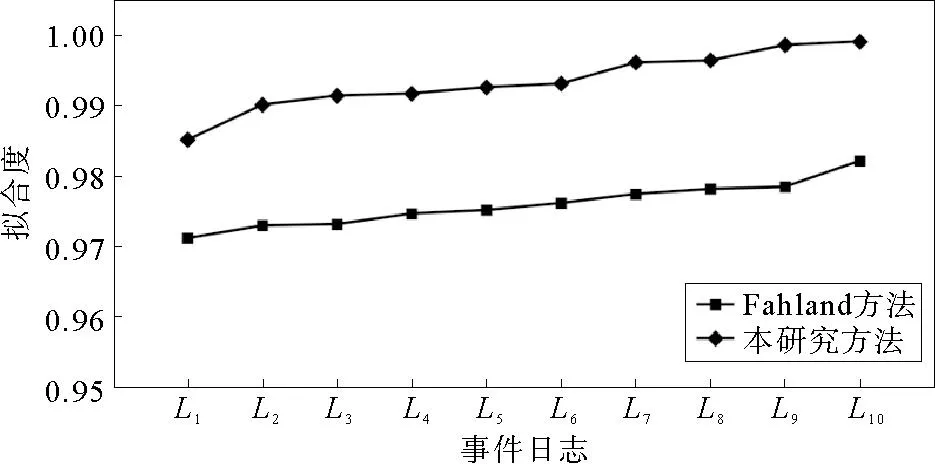
图8 拟合度变化曲线

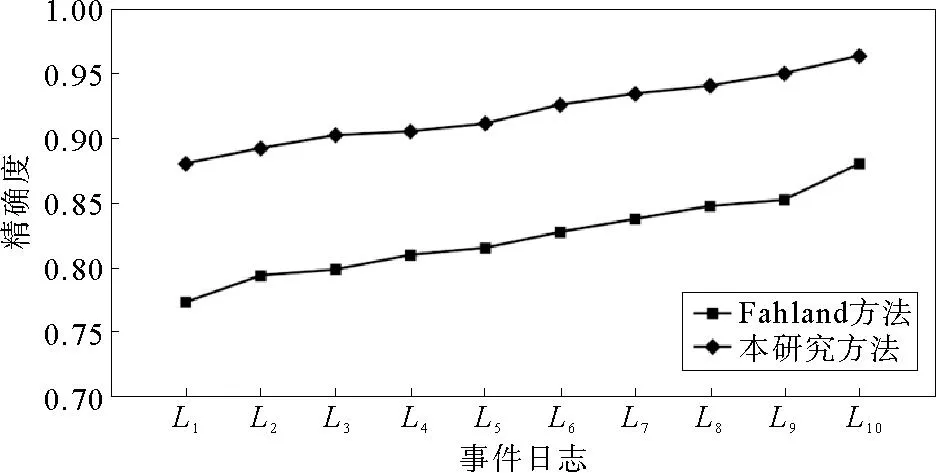
图9 精确度变化曲线

从修复模型的库所、变迁、流关系上对两种方法进行简洁度对比,结果如表2所示,可以看出,本研究方法得到的模型简洁度更高。与Fahland方法相比,本研究方法提高了模型的简洁度,同时也表示了不同结构之间的间接依赖关系。

表2 模型简洁度比较

5 结论

本研究针对循环选择驱动循环结构过程模型提出一种新的模型修复方法,将循环选择驱动循环结构分成三部分分别进行修复。由于不同结构确定偏差的方式不同,提出两个定理判断各个结构是否存在偏差。在使用确定偏差变迁算法得到循环偏差变迁和选择偏差变迁后,在不添加不可见变迁和重复变迁的情况下,使用提出的修复算法进行模型修复。实验表明,本研究方法不仅能够保持原始结构,而且能够正确描述各结构之间的间接依赖关系。下一步将研究更加复杂的组合结构,进行模型修复并研究之间的间接依赖关系。