基于SW26010处理器的PANDAS众核并行优化方法及在地质变形分析中的应用

王雪纯,邢会林,戴黎明,郭志伟,刘骏标

(1.中国海洋大学 海底科学与探测技术教育部重点实验室,山东 青岛 266100;2.青岛海洋科学与技术国家实验室 深海多学科交叉研究中心,山东 青岛 266237;3. 中国海洋大学 海底科学与工程计算国际中心,山东 青岛 266100)

地质体变形分析是地球科学问题研究的重要组成部分,包括拉伸、压缩、剪切等体积和形状的改变,复杂变形可以表示为多种简单变形的叠加。有限元方法作为地质体变形分析最重要的方法之一,被广泛应用于地震预测、油气资源勘探与开发、土壤与岩石力学行为模拟等诸多领域。宋孝天等[1]利用扩展有限元法计算裂纹扩展路径,研究了裂隙面变形参数对非贯通裂隙岩体压缩特性的影响。陈云锅[2]通过构建青藏高原内部不同震例震黏性有限元模型来分析震后形变动力学过程,定量约束青藏高原壳幔流变属性以及震后余滑分布和演化。随着模型规模的增大,单机系统难以满足算力和存储的要求,利用并行计算技术和超级计算机系统进行大规模数值模拟计算已成为解决问题的重要手段。为进一步提高计算速度、降低功耗,异构众核处理器逐渐取代同构多核处理器成为超级计算机系统的首选。但异构众核处理器上的并行程序设计需要考虑模块划分、数据划分和线程同步等问题,代码实现相对复杂,已有的同构计算机并行算法无法直接应用于异构众核架构的计算机系统。

SW26010是我国自主研发的高性能异构众核处理器,支持消息传递接口(message passing interface,MPI)、线程加速库(Sunway Athread库)等并行编程模型,能够提供比传统高性能平台更强大的计算能力和访存带宽。王泽松[3]基于申威众核架构特点实现了有限元区域分解方法在超级计算机平台的基于信息传递接口和加速线程库的高效并行求解策略;傅游等[4]基于“神威·太湖之光”高性能计算平台的Open ACC编程模型实现了Tend_lin的并行优化;柳安军等[5]利用共享内存和寄存器通信等技术实现了Palabos软件在新一代神威超算上两相流算法的百万核心规模的并行计算。

并行自适应非线性变形分析软件(parallel adaptive nonlinear deformation analysis software,PANDAS)是一个基于有限元方法和格子玻尔兹曼方法(lattice boltzmann method, LBM)的数值模拟软件,已成功应用于含裂隙的非均质多孔材料模拟中,用于解决应力变形、应力破坏、流体流动、热传导、化学反应等多物理场高度非线性耦合的问题[6]。目前地质体变形分析领域的众核并行计算软件仍存在较大空缺,而传统的多CPU并行方法不适用于异构众核处理器,亟需针对异构众核处理器的体系结构特点研发地质体变形计算的重要算子,即有限元计算的并行方法。本研究基于SW26010异构众核处理器,利用MPI模型和Sunway Athread库对PANDAS软件进行并行优化。通过区域分解、数据压缩存储、系数矩阵预处理和并行共轭梯度法求解方程组等方法提升软件模拟速度,并将众核并行程序应用于全地球运动模型、多孔介质压缩变形和接触体的接触状态改变等常见地质变形分析,为复杂地质体的变形模拟分析提供技术支持。

1 SW26010异构众核处理器及其并行模式

SW26010异构众核处理器由4个核组组成,每个核组包括1个内存控制器、1个运算控制核心(management processing element,MPE,又称主核)、64个从核组成的客户终端设备(customer premise equipment,CPE)、系统管理接口[7],如图1所示。SW26010单芯片双精度浮点计算峰值达3.168 TFLOPS。从核通过内存控制器访问内存并且支持直接内存访问方式(direct memory access,DMA),每个从核具有一个大小为64 kB的局部数据存储器(local data memory,LDM),通过DMA方式完成主存向从核LDM空间的数据传输,能够更好地利用带宽,加快数据传输速度。但是从核LDM空间大小有限,无法一次性满足大规模计算的存储要求,频繁启动DMA将导致程序性能下降,因此需要在每次传输时尽可能多的传输数据。

图1 SW26010处理器单核组结构示意图

SW26010处理器使用MPI+X并行模式完成大规模并行计算,该模式下主核调用MPI接口实现跨核组通信、调用Sunway Athread库实现从核并行计算以及从核资源控制。主核调用从核资源分为三个过程:从核资源初始化、从核执行数据运算、回收从核资源,分别由主核调用athread_init()、athread_spawn()、athread_halt()三组函数实现。Sunway Athread库提供了线程级加速方法。

2 SW26010处理器的PANDAS众核并行优化方法

PANDAS计算主要包括生成单元刚度矩阵、总刚度矩阵组装以及方程组求解三个过程。求解方程组时采用共轭梯度法经过多次迭代获得近似值,该算法无多级嵌套循环,易于实现并行,但每次迭代都依赖上次迭代结果,因此迭代过程无法并发。

本研究采取的并行策略为:简单的逻辑控制和只需少量迭代的步骤仍串行执行,大量迭代的操作并行执行。首先将串行代码移植到SW26010主核上,然后利用区域分解技术、矩阵压缩存储技术、系数矩阵预处理和并行化共轭梯度算法实现PANDAS的众核并行优化。 通过区域分解将大规模网格数据分解到多个核心上并行计算,调用MPI接口实现数据交换,使用压缩存储技术降低内存消耗,利用众核处理器的主从核异构架构优化共轭梯度算法,加快方程组求解速度,实现更高性能的并行计算。

2.1 区域分解和稀疏矩阵压缩存储

区域分解以节点为单位,将大的计算区域分解成多个规模较小的子区域用于并行计算[8],按照选定的轴向和数量划分区域并记录各个子区域的通信表,子区域之间节点不重复,划分时不考虑接触情况,分割后更新通信表并形成各个子区域的边界条件和材料属性等信息。区域划分后,节点分为三类:边界节点、内部节点和外部节点。计算过程中,内部节点与外部节点之间需要进行数据交换(图2),同时边界节点所在单元被记录到构成该单元节点的所有分区中。每个主核处理一个子区域,主核间通过MPI_ISEND接口发送数据和MPI_IRECV接口接收数据,实现不同子区域间的数据交互,为分解生成的n个区域分配n+1个(编号0～n)进程共同完成计算。其中,0～(n-1)号进程作为计算器执行运算任务,生成区域刚度矩阵并通过迭代求解器计算推导出的线性方程组;n号进程作为控制器,收集来自其他进程的向量并进行接触搜索,运算器和控制器二者结合将原问题求解转为子区域并行求解。

图2 模型区域分解及数据交换[6]

2.2 系数矩阵选择性分块预处理方法

程序中通过定义接触面组合表示每对接触面,其中包含一个主接触面和一个从接触面。使用罚因子方法处理接触关系,通过两个点在接触面法线方向上的相对位移大小判断是否接触。发生接触时需要满足法向接触力F=f·n=E·g,其中E为法向上的罚因子,g为外法线穿透量,f为接触力,n为接触面外法线方向[9]。首先通过全局搜索找到可能发生接触的从节点和主接触面,然后通过内外算法[10]计算从节点是否存在主接触面来判断潜在接触对间的两个面有无接触。接触问题被归结为附带约束条件的线性问题,系数矩阵的条件数通常很大,这将直接影响迭代过程的收敛速度。使用预处理技术会增加部分计算开销但却可以加快迭代求解收敛速度,因此通常在求解前对大规模系数矩阵进行预处理。预处理采用选择性分块方法,从总刚度矩阵对角线位置的非零节点出发横向搜索,将被罚因子λ约束的同一接触组中的节点放在一个以该节点为起点的块中。若节点之间相邻则仍保持相邻位置关系,否则按照搜索顺序排列,如图3所示。重排序后生成的稀疏矩阵的非零项集中在以对角线为中心的带状区域并对新矩阵执行LU分解。

图3 选择性分块预处理方式

2.3 SW26010处理器上的并行共轭梯度算法

PANDAS中的大规模迭代求解器基于一般方程Ax=b的共轭梯度法实现。主核调用从核函数对方程组进行求解,具体的迭代求解步骤由从核完成。主核将计算任务平均分配给从核,使用Sunway Athread库athread_get_tid()接口获取从核编号,按照编号分配对应区段的数据(图4),未被分配的数据由主核完成计算。每个主核启动从核进行主要迭代操作,通过循环将需要计算的数据依次批量读入从核私有的LDM存储空间,减少直接存取主存空间的次数,从核对读入的数据运算后,将处理完的数据批量写回主存空间。按照串行共轭梯度算法的计算流程编写并行算法,迭代过程中涉及到的矩阵运算、数组遍历等大规模的循环操作由每个主核的从核阵列并行完成,主核间通过MPI接口进行数据交换以实现区域之间的数据传递。

图4 从核任务划分图

对于每个主核计算的部分方程组,用系数矩阵的行号除以m+1取余数,根据余数分配到对应编号的从核。从核执行向量的乘加运算,所有从核的行为相似,仅处理的数据不同。将共轭梯度法的迭代过程按照数据关联关系分解为多个从核函数,根据每个函数需要传递的参数个数计算每个从核函数每次可以传输的最大数据量,从核调用athread_get()和athread_put()函数每次按照最大数据量读入LDM空间和写回内存,依次循环直至所有数据计算完毕,释放从核资源。主核将计算得到的局部解向量集合获得最终结果。

综上所述,本研究提出的众核并行优化方法为:通过区域分解将大模型分解为多个规模较小的模型分配给主核并行计算,降低单个核心计算数据量;利用压缩存储技术将原本的大规模稀疏矩阵压缩为三个一维矩阵,节省存储空间;通过对系数矩阵的预处理加速迭代求解过程的收敛速度,减少迭代次数、缩短迭代时间;利用SW26010从核阵列实现大规模方程组的迭代求解,将串行共轭梯度算法分解为多个从核函数执行,主核之间通过MPI实现数据在不同区域之间的传递。最终0号主核集合来自其他主核的解向量合并输出,得到方程组的解向量。

3 PANDAS众核优化方法在地质体变形分析中的应用及性能测评

为了测试上述方法的效果,将PANDAS模拟程序分别应用于SW26010异构众核处理器(1.54 GHz)的单个核组和Intel Xeon Platinum 8268处理器(2.9 GHz),并对优化并行后PANDAS模拟结果的可靠性和速度提升效果进行测试。

3.1 全地球模型速度场模拟分析

全地球模型从内到外由内核、外核、地幔(下地幔)、转换带、软流圈、岩石圈地幔和地壳组成,其中转换带、软流圈、岩石圈地幔和地壳的深度界面根据LITHO1.0[11]得出。对板块边界的网格进行加密处理,将其离散为11 768 300个节点、10 072 140个单元和38个非连续接触面。板块边界每层的属性取自PREM模型[12],材料参数信息如表1所示。根据NNR-MORVEL56模型[13]中各板块的欧拉极点角速度对地球表面节点施加速度边界条件。

表1 地球内部圈层划分及物理性质

通过区域分解将模型划分为64个子区域,使用众核并行PANDAS对模型模拟计算。墨卡托投影得到地球表面的运动速度场。经过对比,计算获得的板块速度与实际GPS结果[14]基本一致。实验结果表明,众核并行计算的模拟结果与真实情况基本吻合,该方法能够应用于复杂变形分析。

3.2 多孔介质压缩分析

岩石中分布着硬度不同的物质,这些物质受到拉伸或者压缩时产生不同的变形,导致岩石在压缩过程中位移发生不均匀变化。对取自塔里木盆地的碳酸岩样本(分辨率为9 μm)的CT扫描结果进行二值化处理[15],设计用于测试的网格模型。模型材料参数见表2,生成节点数为16 974 593、单元数为16 777 216的八节点六面体网格模型。模型底部固定,从顶部施加z轴负方向的压力。

表2 测试模型参数信息

用众核并行的PANDAS模拟岩石模型在压缩过程中的变形情况,将模型按照坐标递归二分法在x、y方向四等分,在z方向二等分,共划分为32个区域。由图5可以看出,岩石中存在硬度不同的两种材料,在压缩时其内部位移发生不均匀变化。经计算,优化后的众核并行程序速度提升8.1倍。

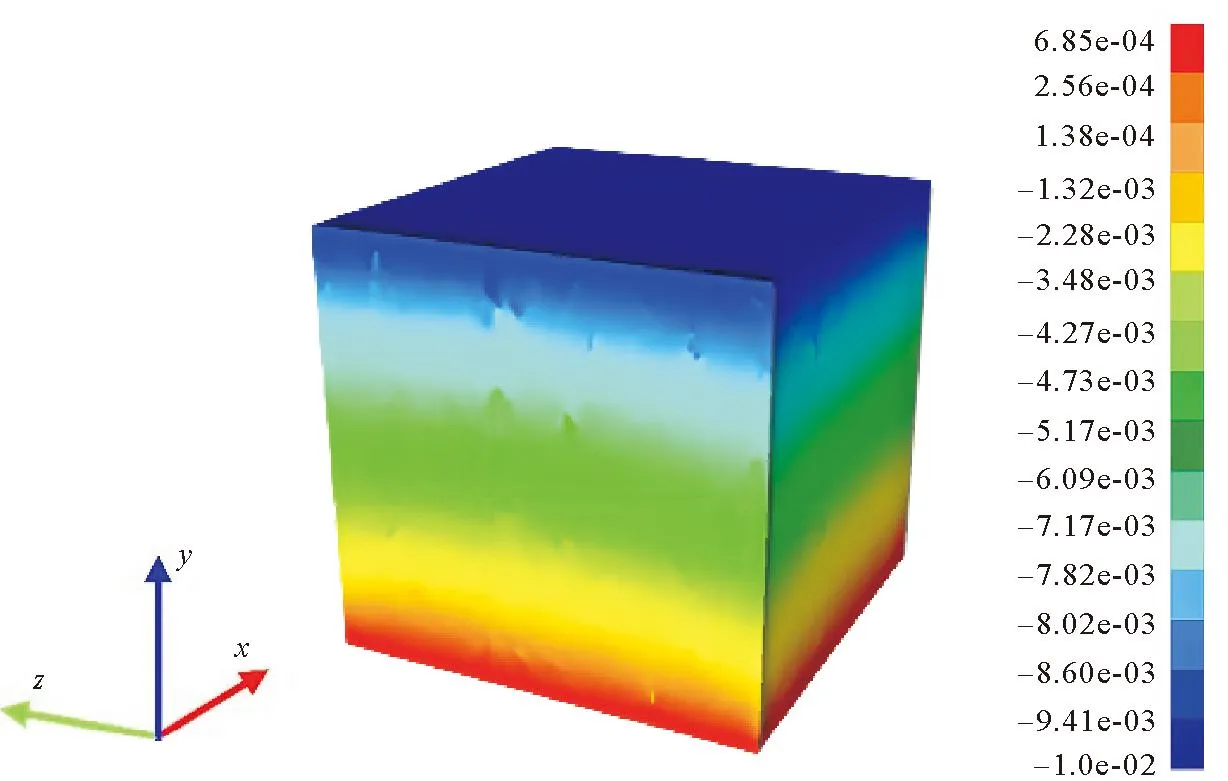
图5 z方向位移场分布

3.3 断层系统运动变形分析

基于岩石夹层摩擦实验模型[6]对网格进行精细划分,生成用于测试的千万网格三维断层系统模型。采用速率相关摩擦定律[9]描述沿接触面的非线性摩擦接触问题。假设材料的性质相同,密度ρ=2 600 kg/m3,杨氏模量E=2 070 MPa,泊松比γ=0.2。模型的节点数为11 054 164、单元数11 033 920,生成两个接触体网格G1、G2并设置一组接触面。边界条件设置为:第一阶段模型左侧物体G1沿着x方向加载,G1加载面上所有节点沿x方向固定,右侧物体G2沿y方向移动;第二阶段G2从相对静止状态以1.0 mm/s的速度沿着y轴负方向移动。

使用众核并行PANDAS程序模拟两个接触体的运动状态变化,在x、z方向二等分、y方向四等分将模型划分为16个区域,使用选择性分块预处理方法对系数矩阵进行变换。y方向的速度变化结果如图6所示。从图6(a)可以看出,在第二阶段加载刚开始时,y方向的速度场连续分布,两个物体之间未发生明显滑动;随着加载的进行,如图6(b)所示,G1接触面上方区域首先由闭锁状态进入局部滑动状态,接触面出现局部的速度不连续;图6(c)表明,随着加载持续进行,两个接触体逐渐开始滑动脱离,接触面两侧发生较大的速度突变。

图6 不同场景下y方向速度场

设置收敛条件满足精度高于1.0×10-10,迭代过程中的相对残差数据如图7所示。可以看出,使用选择性分块预处理方法时,迭代求解过程中的残差数据基本呈线性分布,收敛效果良好。对模型进行不同数量的区域分解并测试(表3),在最优情况下众核并行程序收敛一次所需的时长为CPU串行程序的11.6%,速度提升7.6倍,表明众核程序在分析接触问题时具有明显的加速效果。

表3 计算时长对比(众核并行/CPU单核串行)

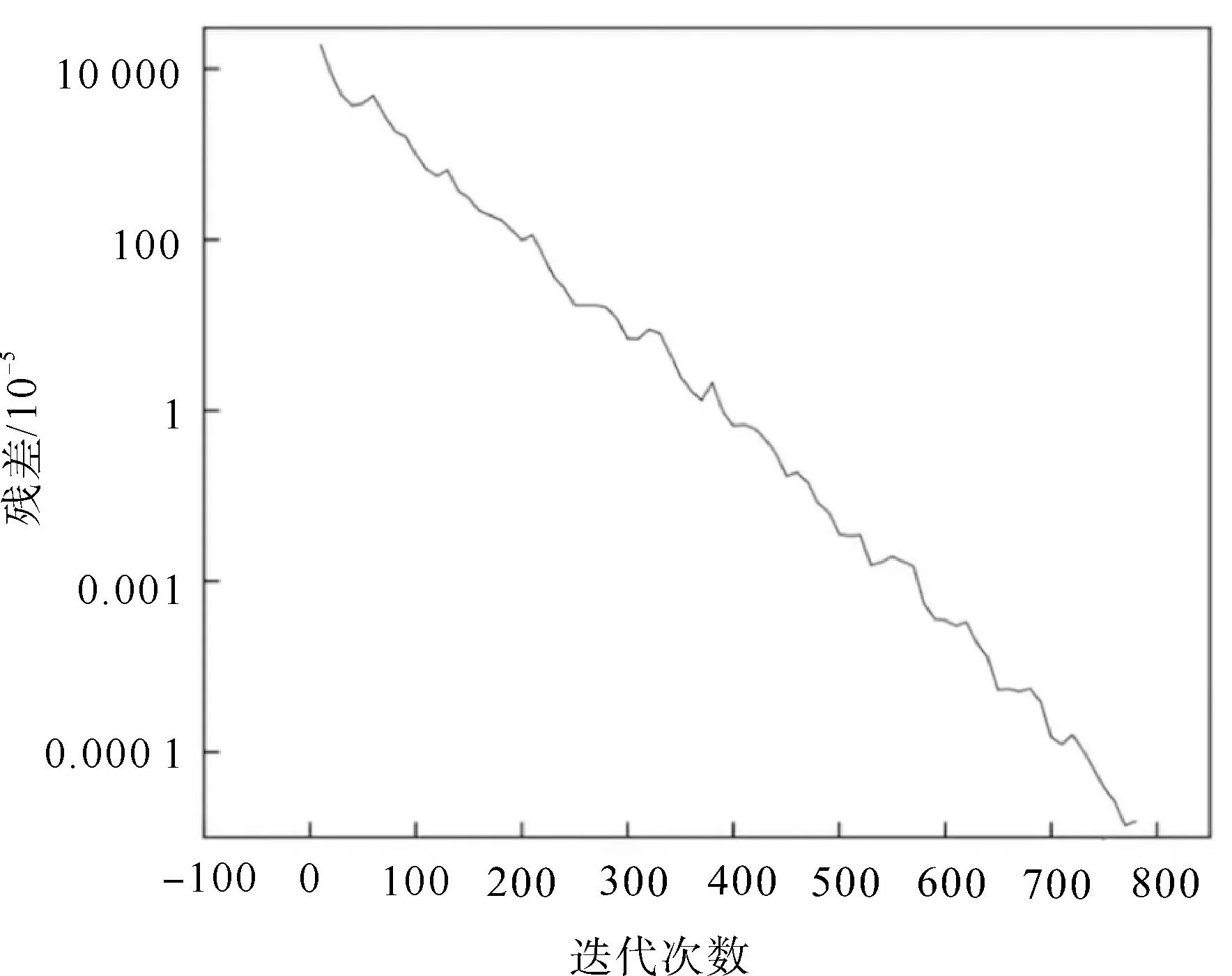
图7 选择性分块预处理方法残差曲线

上述模型的测试结果表明,众核并行优化后PANDAS程序的计算能力明显提升。众核程序能够正确分析大规模的复杂地质体变形,对大规模单一地质体变形和复杂接触体变形的模拟均获得较好加速效果,可大幅缩短模拟时间。在对断层系统模型的测试中,当使用64个核心并行计算时,加速比开始降低,可能由于当前规模大小的模型,随着并行核心数量的增加,进程间的通信、等待时间占比增大造成的,说明本程序仍有进一步优化空间。

4 结论

本研究针对PANDAS进行千万级大规模模型模拟时求解方程组耗时长的问题,从区域分解、矩阵压缩存储和优化迭代求解几个方面,基于SW26010处理器对求解方程组相关部分核心代码进行并行优化,并采用全地球运动模型、多孔介质压缩模型和断层系统模型对优化后的程序进行验证。相较于传统单一多线程或多进程的并行方法,本研究的众核并行方法结合线程、进程两种并行方式,充分发挥不同处理器的优势,提高了计算速度。全地球模型速度场模拟结果与实际GPS数据基本吻合,优化方法具有可行性;多孔介质压缩模型测试数据表明,众核并行程序在分析单个物体变形问题时计算速度提升了8.1倍;断层系统模拟测试数据表明,优化后的程序在分析多个物体接触问题时速度提升了7.6倍,获得良好的加速效果。以上结果表明,本研究方法可在地质体变形分析的大规模计算中发挥积极作用。然而实际的地质变形问题涉及的网格模型更加复杂,接触面数量也更多,仍需在现有研究基础上设计适用不同模型特征方程组的并行求解算法和区域分解方法。