分割法与合成法求电场强度

郑 金

(辽宁省凌源市职教中心)

对于匀强电场中平行于电场线的平面内的三个点,如果已知各点处的电势,或者已知带电粒子分别经过各点时的动能,或者已知带电粒子分别沿两条线段运动过程中电场力做的功,那么可求出电场强度的大小和方向.对这类问题有两种不同的解答方法,即电势差分割法与场强分量合成法.

1 方法归纳

方法依据:匀强电场中的任意一条直线上的电势降落规律相同,两点之间的电势差跟距离成正比.

1)电势差分割法.首先选择三个点中电势最高点为参考点,以参考点为起点,确定两条线段;再计算每条线段两端的电势差,根据电势差数值的特点均匀分割线段;然后在两条线段上寻找两个等势点,连接一条等势线;最后画出一条电场线,计算沿电场线方向某一线段的长度,求出场强大小和方向.

2)场强分量合成法.首先分别算出两条相互垂直线段两端的电势差;再计算电场强度在两个相互垂直方向的分量;最后利用矢量合成法求出合场强的大小和方向.这种方法的关键是如何计算某一方向的场强分量,需利用一个结论,下面进行定量推导论证.

如图1所示,在匀强电场中与电场线平行的平面内有一条线段AB,线段AB的长度为LAB,与电场线的夹角为β,利用场强公式可知线段AB两端的电势差UAB＝Ed＝E•LABcosβ＝Ecosβ•LAB,即UAB＝EABLAB,或者.

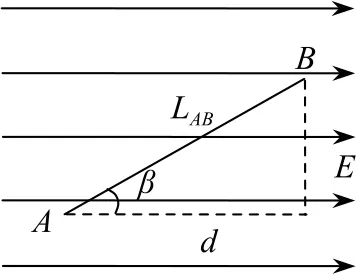
图1

这表明,在匀强电场中任意两点间的电势差等于这两点连线上的场强分量与这两点间的距离之积.换言之,在匀强电场中任意两点间的电势差与这两点间的距离之比等于电场强度在这两点连线上的分量,这就是场强分量结论.

值得注意的是,对于匀强电场,虽然可以求出任一方向上的场强分量,但不能分解为任意夹角的两个分量,而只能按两个相互垂直的方向进行分解,即正交分解.或者说,两个方向的场强分量夹角必须为直角,否则不遵循平行四边形定则.因此,只要求出场强在某一方向的分量,那么另一个分量的方向就已经确定了.同理,对于点电荷在匀强电场中受到的电场力也只能进行正交分解与合成,只有两个分量相互垂直,各分量的效果才互不关联、互不影响.或者说,一个力在与之垂直的方向上不做功,则两个相互垂直的恒力各自做功是独立的.这如同重力,只能进行正交分解与合成,当物体沿斜面下滑时,无论斜面倾斜角如何变化,重力的两个分力都相互垂直,夹角不可能为钝角或锐角.

在匀强电场中场强处处相同,空间任一点的场强都可分解为相互垂直的两个分量,而且同一方向的分量处处相同,即Ex＝Ex1＝Ex2＝…＝Exn,Ey＝Ey1＝Ey2＝…＝Eyn,则合场强为.

2 方法应用

下面对有关的物理问题利用电势差分割法与场强分量合成法求电场强度.

例1(2021年湖南卷)如图2所示,圆心为O的圆处于匀强电场中,电场方向与圆平面平行,ab和cd为该圆直径.将电荷量为q(q＞0)的粒子从a点移动到b点,电场力做功为2W(W＞0);若将该粒子从c点移动到d点,电场力做功为W.下列说法中正确的是( ).

A.该匀强电场的场强方向与ab平行

B.将该粒子从d点移动到b点,电场力做功为0.5W

C.a点处的电势低于c点处的电势

D.若只受电场力,从d点射入圆形电场区域的所有带电粒子都做曲线运动

根据做功情况可知,沿线段ab方向电势逐渐降低,沿线段cd方向电势逐渐降低.利用电场力做功的公式W＝qU可知,两条直径对应的电势差之比为Uab∶Ucd＝2∶1.对于O、b、d三点,O点的电势最高,可作为参考点,由此确定两条线段,即两条半径Ob和Od,对应的电势差之比为UOb∶UOd＝2∶1.据此可将线段Ob均分为两份,设中点为e,则点e与d是等势点,连接de得到一条等势线,如图3所示.可以证明,△Oed为直角三角形,则等势线de垂直于线段ab,因此电场线沿ab方向,选项A 正确.将该粒子由d点移动到b点,等效于从e点移到b点,电场力做功0.5W,选项B正确.过c点作等势线cf,由于a点电势高于f点,可知a点电势高于c点,选项C错误.若带电粒子沿与电场线平行方向射入,则粒子做直线运动,选项D 错误.

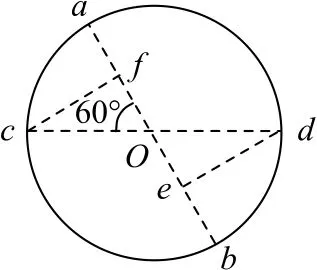
图3

本题解题关键是利用电场力做功的情况来判断电势的变化情况,并得出两个电势差的关系.为了在两条线段上寻找等势点,需在三个点中选择电势最高的点作为参考点.该题虽然不必求解场强,但需利用电势差分割法确定电场线的方向.

例2匀强电场中一个三角形的顶点为A、B、C,AB的长度是1cm,D点是AB的中点,如图4 所示,已知电场线平行于三角形ABC所在平面,A、B、C三点处的电势分别为14V、6V 和2V.设场强大小为E,一电荷量为1.0×10－6C 的正点电荷从D点移动到C点,电场力做的功为W,则( ).

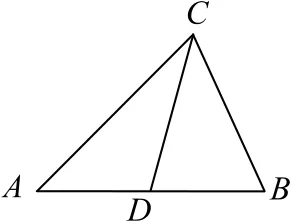
图4

A.W＝8×10－6J,E＞8V•m－1

B.W＝6×10－6J,E＞6V•m－1

C.W＝8×10－6J,E≤8V•m－1

D.W＝6×10－6J,E≤6V•m－1

线段AB的中点D处的电势为φD＝10V,可知UDC＝8V,所以正点电荷从D点移动到C点的过程中电场力做的功为W＝8×10－6J.由题意知,A点处电势最高,以A点为参考点,线段AB和AC对应的电势差分别为UAB＝8V,UAC＝12V,因此可把线段AB二等分,AC三等分,如图5所示,可知G点与D点是一对等势点,电势为φG＝10V,根据电场线垂直于等势面,可画出一条电场线.设两个相邻的等势面间距为Δd,可知电场强度为由于,故E＞8V•m－1,选项A 正确.

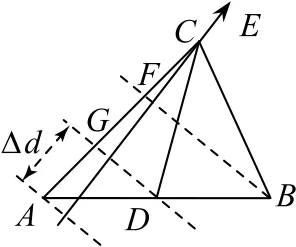
图5

本题解题关键是求中点的电势以及三等分点的电势来确定一条等势线.不必求出场强的具体数值,只需利用场强公式判断场强的取值范围.

例3如图6所示,在匀强电场中画一个等腰直角三角形,三角形平面平行于电场线.已知三角形的直角边长为10cm,顶点A、B、C的电势分别为5 V、20V 和2V.试在图中画出一条电场线,求出场强的大小和方向.

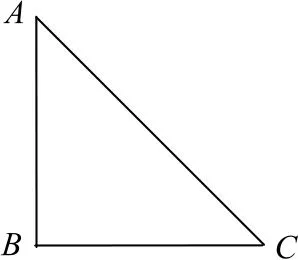
图6

方法1利用电势差分割法

由于B点电势最高,则可作为参考点,以B点为起点,确定两条线段BA和BC.分别计算每条线段两端的电势差,UBA＝15V,UBC＝18V.二者之比为UBA∶UBC＝5∶6.可把线段BC均分为两份,设中点为D,把线段BA均分为5份,设五分之三分点为F,如图7所示.可知UBD＝UBF＝9V,那么D点与F点为等势点,连接线段DF,得到一条等势线.过B点作线段DF的垂线,标明方向,得到一条电场线,与等势线相交于G点.对于直角三角形FBD,斜边长度为,利用两种方法计算直角三角形的面积可知线段BG的长度为.已知UBG＝UBD＝9V,可知场强大小为.场强方向跟BC边的夹角满足,即电场线的倾斜角为.

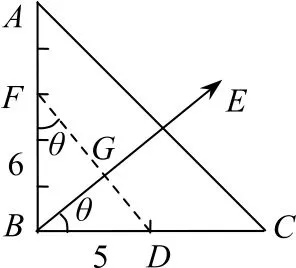
图7

这种方法的解题关键是以电势最高点为参考点,在有共同起点的两条线段上寻找一对等势点,确定一条等势线,再过特殊点确定一条电场线.在计算线段BG的长度时,利用了计算直角三角形DBF面积的两种方法.此外,也可利用各直角三角形中三角函数关系来计算线段BG的长度.

“创新是科德宝在中国成功发展的关键要素。中国客户认为我们的品牌和产品质量一流。”科德宝集团亚洲地区代表许倍帝（Bettina Schoen-Behanzin）强调，“确保客户享受到科德宝正品的高品质非常关键。保护我们的知识产权即专利和商标，对我们和客户都很重要。”

方法2利用场强分量合成法

分别计算两个相互垂直方向的电势差UBC＝18 V,UBA＝15V.可知场强分量大小EBC＝180V•m－1,EBA＝150V•m－1.利用勾股定理可知场强大小

这种方法的解题关键是找到两条相互垂直的线段,分别求出两个方向的场强分量.

例4(2017年新课标全国卷Ⅲ)一匀强电场的方向平行于xOy平面,平面内a、b、c三点的位置如图8所示,三点的电势分别为10V、17V、26V.下列说法正确的是( ).

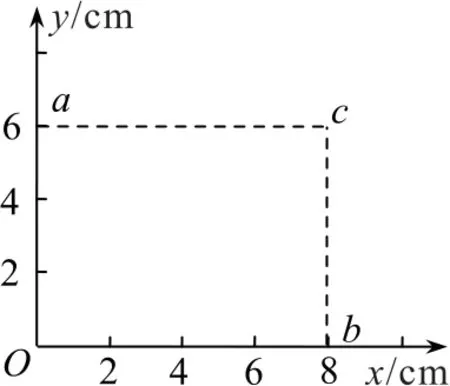
图8

A.电场强度的大小为2.5V•cm－1

B.坐标原点处的电势为1V

C.电子在a点的电势能比在b点低7eV

D.电子从b点运动到c点,电场力做功为9eV

方法1利用电势差分割法由题意知c点处电势最高,线段ca、cb对应的电势差分别为Uca＝16V,Ucb＝9V.如图9所示,可把线段ca平均分为4等份,每份长度为2cm,对应的电势差为4 V;把线段cb平均分为3等份,每份的长度为2cm,对应的电势差为3V.由于数字4与3的最小公倍数为12,则可在线段ca上取3等份,ce＝6cm,Uce＝12V;延长线段cb至f点,使得bf＝2cm,可知cf＝8cm,Ucf＝12V.e、f两点为等势点,连接ef为一条等势线,可知ef＝10cm.

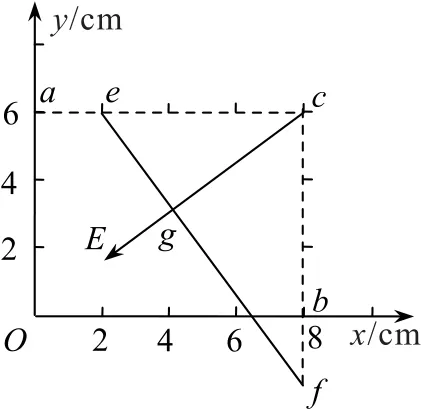
图9

过c点画一条直线垂直于ef,得到一条电场线.设电场线与等势线的交点为g,利用两种方法计算直角△ecf的面积,可知,因此电场强度为.

由此可知选项A 正确.根据“长度相等的平行线段两端的电势差相等”可知,坐标原点处的电势为1V,选项B正确.电子在a点的电势能比在b点的高7eV,选项C错误.电子从b点运动到c点,电场力做的功为W＝eUbc＝9eV,选项D 正确.答案为A、B、D.

在对线段ca与cb进行均匀分割后,为了找到等势点,需延长线段cb,具有一定的技巧性;在计算电场线方向线段长度时,需利用两种方法计算直角三角形的面积.此外,还有一种方法,即在线段ca上找到一点b′与点b处的电势相等,使得Ucb′＝9V,需根据同一直线上两点之间的电势差跟距离成正比计算线段cb′的长度以及利用勾股定理计算线段bb′的长度,推导过程比较烦琐.

方法2利用场强分量合成法

在已知三点中,c点电势最高,计算两个垂直方向的电势差分别为Uca＝16V,Ucb＝9V.可知场强在x、y轴方向的分量大小分别为,,则合场强大小为E＝,选项A 正确.其他选项的判断同方法1.

在计算两个相互垂直方向的场强分量大小时,无须考虑数值中带有负号,但若计算场强分量,则需考虑数值带负号,用来表示方向.

例5如图10所示,4 个点a、b、c、d分布在圆O上,ab＝5cm,cd＝8cm,∠bac＝60°,匀强电场的方向平行于圆所在的平面.已知点a、b、d的电势分别为φa＝46 V,φb＝21V,φd＝10V.求该匀强电场的方向以及场强的大小.

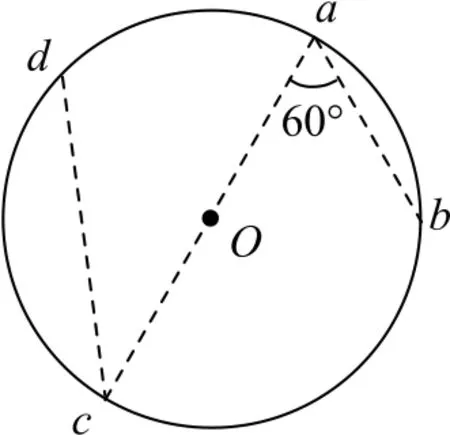
图10

由题意知Oa＝ab＝5cm,则ac＝10cm.a点电势最高,连接线段ad,构成直角三角形,如图11 所示.由于cd＝8cm,可知ad＝6cm,∠dac＝53°.需均匀分割线段ad与ab,以寻找等势点.线段ad两端的电势差为36V,线段ab两端的电势差为25V.可将线段ad均分为6等份,每小段对应的电势差为6V,可知Uae＝30V.把线段ab均分为5等份,每小段对应的电势差为5V.数字5与6的最小公倍数为30,则可在线段ad上取5 等份,Uae＝30 V,对线段ab延长1cm 至点f,可知Uaf＝30V.因此点e、f是一对等势点,连接线段ef得到一条等势线.

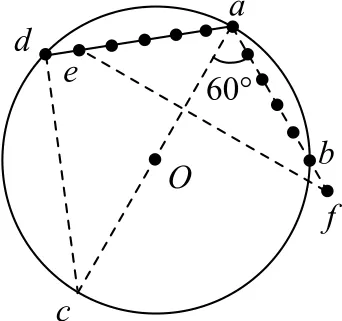
图11

下面利用假设法确定电场线的方向.

假设ac⊥ef,则形成两个直角三角形,用不同方法分别计算公共直角边的长度为

由于所得两个数值相等,因此“假设”成立,即ac⊥ef.可知电场线沿ac方向,从点a指向c.

对于线段af,两端的电势差为Uaf＝30V,在电场线方向的长度为l＝0.03m,可知场强大小为

要注意两个等势点不一定都在线段上,有时可能位于延长线上.虽然在寻找等势点时也可以再把线段ae平分,中点g与线段ab的五分之三分点h是一对等势点,但是在作图方面不理想.对于电场线方向的确定,关键是利用假设法来证明ac⊥ef.

综上可见,对有关“匀强电场中三个点的电势求场强”一类问题,通常可有两种求解方法,其一是电势差分割法,需对共同起点的两条线段进行均匀分割,由此求出等势点,画出等势线和电场线,即可求出场强大小和方向;其二场强分量合成法,实际上是正交分解法,即由相互垂直的两条线段对应的电势差求出场强的两个相互垂直的分量,利用矢量直角三角形求出场强的大小和方向.第一种方法普遍适用于有关各种三角形顶点的电势问题;第二种方法只适用于有关直角三角形顶点的电势问题,若没有直角三角形,则需作某一线段的垂线,即辅助线,确定两个相互垂直的方向.两种方法繁简不同,例如,对于例1、2、5的解答,利用电势差分割法比较简单,但不适用于场强分量合成法;对于例3、4的解答,利用场强分量合成法比较简单,而利用电势差分割法则难度较大.总之,需对各种不同的物理问题进行具体分析,灵活选择合适的方法,可使问题迎刃而解.

(完)