结构化思维培养视角下的解决问题教学新路径
文/中山市南朗街道南朗小学 杜少君
所谓“结构化思维”是指以探索事物结构为目标,积极建构事物组成部分之间的关联,以得出事物发展的一般规律的一种结构思维方法。在解决问题教学中,培养学生结构化思维,需要通过对解决问题教学内容的结构化、教学过程的结构化等策略,以问题为因,以条件为果,通过结构化教学路径,引导学生在解决问题过程中,感受条件与问题知识结点的逻辑关系,培养学生的数学结构化思维。本文以人教版小学数学三年级下册第四单元“用连乘解决实际问题”为例,对数学问题中的条件(因)与问题(果)展开积极的教学实践与探索。
一、提炼因果,结构化思维的信息整理优化
数学问题一般是由条件(因)和问题(果)两个部分组成,通常在教材中以解决问题三步骤中的第一个步骤“阅读与理解”的形式呈现出来。学生通过“阅读与理解”,用抽象的方法对现实生活情境进行数学化,用数学的眼光发现情境中的数学问题并提出问题。因此有效提炼解决问题中的“因和果”,将生活化的问题转化数学问题,将呈现的数学信息整理优化,是学生从感性认识到理性认识,是对数学信息的条件化、结构化的过程,以此促进学生思维的结构化。
【教学片段一】
超市一周卖出5 箱保温壶,每个保温壶卖45 元。(见图1)

图1
师:说一说你知道了哪些信息?
预设1:我知道了保温壶有5箱,每箱里有12 个保温壶,每个保温壶卖45 元。
师:你观察的很仔细,从中找出了有5 箱保温壶,每箱12 个,每个45 元这三个条件。根据这些信息,你能提出什么数学问题?
预设2:一共卖了多少元?
师:你说的“一共”指的是什么数量?
预设3:“一共”是指5 箱,也就是“5 箱保温壶卖了多少元?”
师:还有不同的提问吗?
预设4:我想问“一箱保温壶多少元?”
师:根据大家的发现,我们可以把这些数学信息和问题进行简化(如图2)。
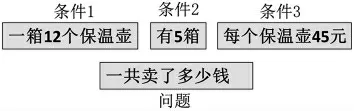
图2
在解决问题“阅读与理解”这一环节中,教师在引导学生观察、思考中,发现了3 个条件,并提出问题。通过简化的数学信息与问题,对数学信息进行结构化整理,呈现出以层次结构网络或图式结构,触发学生更清晰地看到数学问题中的条件与问题,有助于学生提高对条件与问题的之间的内在联系。
二、执果索因,结构化思维的逆向解题途径
数学知识体系并不是孤立的,分割的,而是由内在联系组成的逻辑结构系统。探索和揭示解决问题中的条件(因)和问题(果)的关联过程,就是解决问题的第二个步骤是“分析与解答”,它是问题解决的核心,重在培养学生分析问题和解决问题的能力。
“执果索因”即分析法,指从问题或结论入手,思考解决问题或得出结论需要哪些条件,一步一步地追溯到所有条件都是已知的为止,也就是由“未知”想“需知”,逐步接近“已知”的方法,通俗地讲,就是看问题,想条件。建构解决问题中的条件(因)和问题(果)之间的关联,就是思考用什么样的方法揭示条件(因)与问题(果)之间的内在联系,以此促进学生结构化思维发展。执果索因是学生形成结构化思维的逆向解题的有效途径。
【教学片段二】
师:你们提的问题非常有针对性,一个是“5 箱保温壶卖了多少元”,一个是“1 箱保温壶卖了多少元?”。这两个问题之间有联系吗?
预设5:有关系,要想求“5 箱保温壶卖多少元?”,就要先知道“1 箱保温壶卖多少元”,再把1 箱的钱数乘5,就能求出5 箱保温壶卖的钱数。
预设6:先求1 箱卖了多少钱?用1 个保温壶的单价×1 箱保温壶的个数=1 箱的价钱,列式:45×12=540(元)。
再求一共卖了多少元?用1 箱保温壶的单价×保温壶的箱数=保温壶的总价。列式:540×5=2700(元)
师:怎样列出综合算式?第一步先求什么?第二步求什么?
预设7:综合算式:45×12×5=2700(元)。先算45×12,求出1 箱保温壶的价钱,再用1 箱的单价乘总数量5 箱,得出一共卖出多少钱?
师:回答非常棒,你们从问题入手来寻条件和信息,并找到了解决问题的办法。像这样从问题出发,寻找解题条件和信息来解决问题,这种方法叫做分析法。(如图3)
通过对“一共卖了有多少元”这一问题出发,让学生思考“5 箱保温壶一共卖多少元?”和“1 箱保温壶卖多少元?”之间的联系,引发可以先求“1 箱保温壶卖多少元?”,再乘保温壶的数量5 箱,从而得出“一共卖了有多少元”。即从问题入手,通过逆向思考,层层分析解决问题所必需的条件,执果索因,采用分析法建构解决问题的方案。
三、由因导果,结构化思维的顺向解题表达
在解决问题的方法中,“由因导果”又称之为综合法,即从已知条件入手,思考经过怎样的运算或推理,可以一步一步得到解决问题的答案或结论,这是由“已知”想“可知”,逐步导向“未知”的方法,通俗地讲,就是看条件,想问题。通过收集数学问题的已知条件,思考已知条件1和已知条件2 之间有什么联系?根据已知条件1 与已知条件2 之间的联系,找出隐含的数学问题中的条件3,把条件3 当成一个新的条件,用同样的方法分析条件2 与条件3之间有什么联系,找出隐含的数学问题中的条件4……以此分析下去,直到把问题解决为止(如图4)。通过这一过程探究,培养学生结构化思维的“层次性思维”。

图4
师:同学们,除了从问题出发来解决题问,还可以怎样来思考?
【教学片段三】预设8:我认为还可以从条件出发。根据一周卖出5 箱保温壶,每个保温壶卖45 元,这两个条件,可以用1 箱保温壶的个数×保温壶的箱数=保温壶的总个数,列式为:12×5=60(个);根据已求出的保温壶的总个数和每个保温壶的单价,用保温壶的总个数×每个保温壶的单价=保温壶的总价,就可以求出5 箱保温壶的总价钱。列式为:60×45=2700(元)。
师:怎样列出综合算式?第一步先求什么?第二步求什么?
预设9:列综合算式为:12×5×45=2700(元),先算12×5,求出5 箱保温壶的总个数,再乘每个保温壶的单价,得出一共卖出多少钱?
师:你的思路非常精彩!看来在解决问题的过程中,我们也可以从信息和条件出发,从条件当中找出隐含的条件,逐步解决问题,这样的解题方法称之为综合法。(如图5)
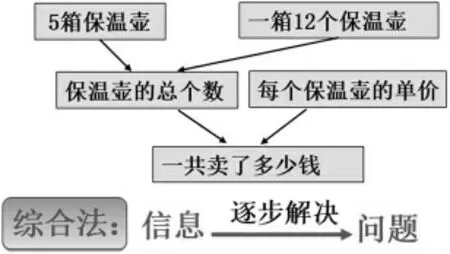
图5
教学片段三呈现了学生从每个保温壶的单价和数量这两个已知条件出发,得出用单价×数量=1 箱保温壶的总价。再把1 箱保温壶的总价转化为1 箱保温壶的单价×5箱的总数量=5 箱保温壶的总价,即求出一共卖了多少元?这一过程呈现了从条件入手,对照问题展开深入分析,从而由因导果,采用综合法构建解决问题的方案。
四、因果融合,结构化思维的核心素养提升
“在数学教学中,以‘结构化的教学’统驭数学‘结构化的知识’,进而催生学生的‘结构化思维’,让数学学科价值最大化,这或许就是结构化数学教学的价值旨归。”分析法(执果索因)和综合法(由因导果)作为解决问题中的两种基本方法、基本思路,其目的是帮助学生从现实情境中的表层结构找出数量组成的深层结构,其中分析是综合的基础,而综合是分析的整合。在解决问题的实际过程中,有时不能孤立地仅从分析法(执果索因)或者仅从综合法(由因导果)来解决问题,教师有必要让学生体会“看问题,想条件”与“看条件,想问题”的综合运用、灵活运用,将条件(因)和问题(果)相互融合,让学生体会分析与综合、分解与整合,经历从局部到整体,从整体到局部的思考过程,进一步引导学生找出解决问题的一般方法,提升学生知识结构化的整理能力,促进结构化思维提升。

