Drive structure and path tracking strategy of omnidirectional AGV
ZHANG Songsong,WU Xiaojun,ZHAO He,WANG Peng,WANG Huan
(School of Mechanical and Electrical Engineering,Xi’an University of Architecture and Technology,Xi’an 710055,China)
Abstract:As an important handling tool in the modern intelligent warehousing and logistics industry,omnidirectional automated guided vehicles (AGVs) have greatly improved the efficiency of warehousing and handling operations.However,the existing omnidirectional AGVs have problems such as insufficient bearing capacity of drive structure,poor path tracking accuracy,and poor correction effect.A new type of omnidirectional AGV with two-wheel differential full steering drive mechanism is designed,and a path tracking control strategy using fuzzy neural network PID (FNN-PID) control is proposed to improve the driving performance and path tracking effect of the omnidirectional AGV.Firstly,the new differential full steering drive structure is designed,and its kinematics model is established,the new drive structure has better load-bearing performance.In addition,according to the established kinematics model,the relationship between speed and rotation angle in four different motion modes is analyzed.Finally,the FNN-PID control strategy is used to track and correct the omnidirectional AGV path,and the conjugate gradient (i.e.,FR) method is used to learn and train neural network weights,which can improve the response performance of the control system.The proposed control strategy is compared with the traditional PID control strategy through simulation and semicircular path tracking experiments.The simulation and experimental results show that the proposed control strategy can quickly eliminate the deviation in 2 s.The distance deviation is within 1 cm,and the heading deviation is about 1° in the stable tracking stage.The new full steering drive structure has better drive performance and the FNN-PID control strategy using the FR method to learn and train can more effectively track and control the path.The new structure and control method have a certain significance for the precise handling of omnidirectional AGVs.
Key words:omnidirectional automated guided vehicles (AGVs); drive structure; full steering differential mechanism; fuzzy neural network; multi-variable input; path tracking
0 Introduction
In recent years,automated guided vehicles (AGVs) with autonomous obstacle avoidance functions have been widely used in unmanned chemical factories,warehousing,logistics industries,and manufacturing industries[1-2].The omnidirectional AGV has an important impact on the development of handling operations.In some special occasions,such as narrow routes and no turning conditions,AGVs with omnidirectional motion functions are required.Therefore,the research on omnidirectional AGVs has great practical significance[3].At present,omnidirectional wheels such as mecanum wheel and steering wheel are used to realize the omnidirectional movement of AGV,but the mecanum wheel has obvious shortcomings in bearing capacity,and driving torque,and the steering wheel has strong coupling effect and expensive cost[4].Therefore,a new type of differential full steering mechanism is proposed,which has the advantages of simple structure,strong bearing capacity and low price.It is used in omnidirectional AGV,and its kinematics performance is verified.
The accuracy of AGV path tracking has an important impact on the development of intelligent handling systems.Many scholars have studied the AGV’s motion posture and path tracking correction control[5].A new 4WIS-AGV path tracking control strategy is designed and the effectiveness of the control strategy is verified in tracking sharp edges and circular trajectories through simulation and experiments[6].The path tracking of autonomous vehicles is controlled based on the MPC control strategy,and the algorithm is optimized to improve the performance of the controller[7-8].The path tracking control of autonomous vehicles is proposed based on MPC-based nonlinear filter control[9].These algorithms have good effects in path tracking.The MPC algorithm relies on accurate vehicle models and parameters,and this step is often complicated and difficult.So it is not suitable for AGV path tracking control.
Fuzzy control does not need to establish an accurate system model and is widely used in path tracking[10].The pose error and feed forward control are taken as input,and a continuous curvature curve local path planning method is designed to track the path of a single steering wheel[11].A hierarchical improved fuzzy dynamic sliding mode control strategy is proposed to study the path tracking and optimize the influence of the uncertainty of the system parameters[12].An improved intelligent hybrid error control strategy is proposed to improve the accuracy of omnidirectional AGV path tracking[13].An under-driving control strategy is proposed with uncertain parameter models for vehicle path trajectory tracking control[14].However,these algorithms have limitations in real-time control and environmental adaptability,and they are difficult to be applied in practice.
Fuzzy neural network has strong self-learning and reasoning capabilities,and has a good effect in solving the deviation problem in trajectory control[15-18].The PID algorithm is simple and robust,and it is widely used in control systems.However,the parameters are difficult to adjust adaptively,so the fuzzy neural network is used to adjust and optimize the PID parameters in real time.An improved fuzzy neural network is designed to optimize PID parameters,and the simulation results show that it has a good effect on PID parameter optimization[19].The PID controller of fuzzy neural network algorithm is used to track and control the motion trajectory of the manipulator,and the simulation verifies that the algorithm has a good effect in controlling the trajectory of the manipulator[20].In the AGV path tracking,there are few researches on the fuzzy neural network PID control with self-learning ability and high robustness.Therefore,based on the new omnidirectional AGV designed in this paper,the fuzzy neural network PID control strategy is used for path tracking.The path tracking and correction effect of the proposed algorithm in omnidirectional AGV are verified by simulation and experiment.
1 Full steering drive structure
The designed omnidirectional AGV is driven by an eight-wheel hub motor.On the basis of increasing the carrying capacity and driving torque,the hub motor is combined and designed to achieve the omnidirectional function of the steering mechanism.The whole vehicle has four sets of steering mechanisms,and each set of steering mechanisms consists of two hub motors,two shock absorbers,drive bracket,and angle sensor.The hub motor has a built-in Hall sensor,the speed can be adjusted in real time,the shock absorbers can make the eight wheels evenly distributed on the ground,and the drive bracket is equipped with an angle sensor to ensure the accuracy of the steering angle.When the AGV running,the eight hub motors are all driving wheels.When turning,the two hub motors of the steering mechanism realize the mechanism steering through the differential speed,and the steering angle is ±90°.At this time,the angle sensor mounted on the drive bracket has perform detection and feedback,and then controls the speed of the hub motor to complete the AGV steering.Fig.1 is the model diagram of the full steering drive structure.
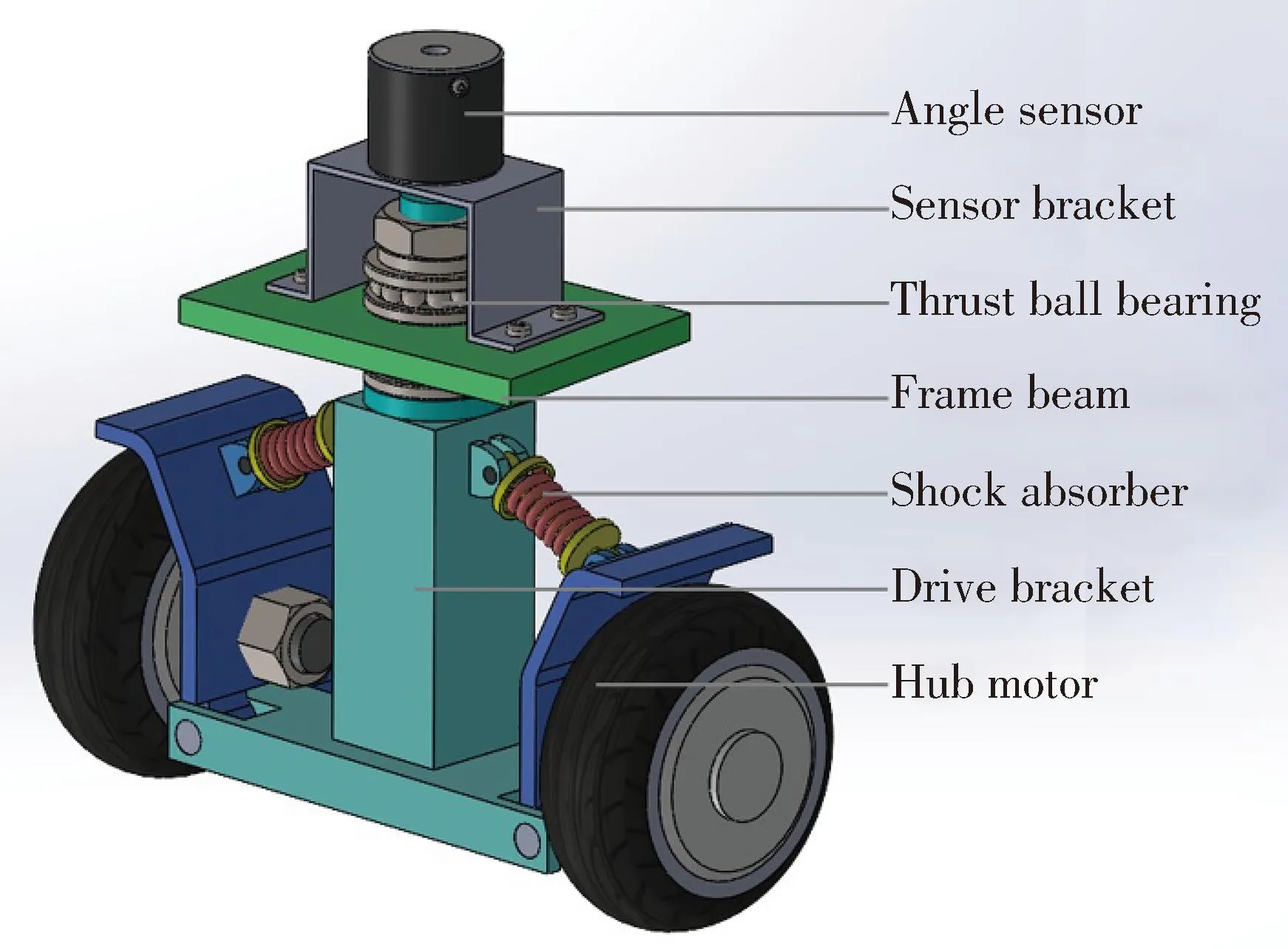
Fig.1 Full steering drive structure model diagram
2 Kinematics model
When establishing the kinematics model,it is necessary to make assumptions about the entire vehicle model.Assume that the frame structure is a rigid body,the hub motor tires are rigid bodies,the omnidirectional AGV moves on a horizontal plane,there is no pitch change,and the impact of the shock absorber on the deformation of the drive structure is ignored[21].On this basis,the steering kinematics model of the omnidirectional AGV is established.
2.1 Kinematics model of steering mechanism
The steering mechanism of omnidirectional AGV adopts differential drive to realize real-time adjustment control of steering and curve tracking movement.The direction of rotation and the radius of curve movement are realized by the different speeds between the two wheels.
Fig.2 is kinematics model diagram of steering mechanisma.It can be seen that the kinematics equation can be given as
(1)

Fig.2 Kinematics model diagram of steering mechanism a
wherevais the speed of the axis of the steering mechanism of a;valis the speed of the left hub motor of the steering mechanism of a; andvaris the speed of the right hub motor of the steering mechanism a.
In addition,the steering angular velocity equation of mechanism a can be expressed as
(2)
whereBis the wheelbase of the two hub motors in the steering mechanism a.
When the AGV is stationary and the four sets of steering mechanisms are turning,only the steering mechanism is in rotational motion (two-wheel hub motor speeds are reversed) to prepare for steering in special operating situations,such as lateral movement.When the four sets of steering mechanisms are all rotating 90°,the AGV can move laterally without changing its pose.
2.2 Kinematics model of omnidirectional AGV
The initial angle of the eight-wheel omnidirectional AGV steering isθ.The reference speed of the AGV is assumed as constantv.Four kinematic models under different motion situations can be obtained.
2.2.1 Kinematics model of front drive mechanism steering
For the eight-wheel hub motor and four-drive steering structure model,when the AGV uses front-wheel steering,the two front driving mechanisms are steering,and the two rear driving mechanisms are kept straight.The steering center of the AGV is on the axis of the two rear driving mechanisms.
Fig.3 is kinematics model diagram of front drive mechanism steering.When using two front drive mechanisms to steer,the turning radiusRcan be described as
(3)
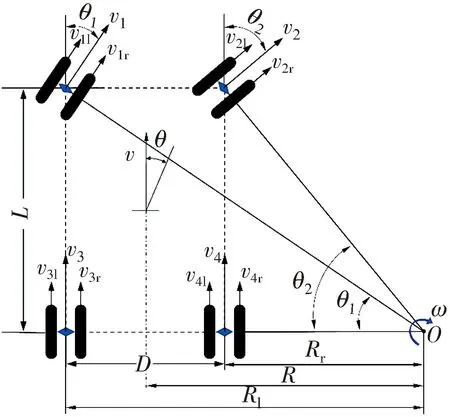
Fig.3 Kinematics model of front drive mechanism steering
The steering angular velocityωof the AGV can be expressed as
(4)
(5)
whereRl,Rr,andDare the left turning radius,right turning radius,and the wheelbase of the left and right steering mechanism,respectively.
According to Eqs.(4) and (5),the angle and speed of each steering mechanism can be given as
(6)
(7)
whereθ1,θ2,θ3,andθ4are the front left steering angle,the front right steering angle,the left rear steering angle,and the left rear steering angle;v1,v2,v3andv4are the center speed of the left front steering mechanism,the center speed of the right front steering mechanism,the center speed of the left rear steering mechanism,and the center speed of the right rear steering mechanism.
The speed of each hub motor can be expressed as
(8)
wherev1lis the line speed of the left wheel of the front left steering mechanism;v1ris the line speed of the right wheel of the front left steering mechanism;v2lis the line speed of the left wheel of the front right steering mechanism;v2ris the line speed of the right wheel of the front right steering mechanism;v3lis the linear velocity of the left wheel of the left rear steering mechanism;v3ris the linear velocity of the right wheel of the left-rear steering mechanism;v4lis the linear velocity of the left wheel of the right-rear steering mechanism;v4ris the linear velocity of the right wheel of the right-rear steering mechanism.
2.2.2 Kinematics model of four-drive mechanism steering
In the normal driving mode,for the omnidirectional AGV driven by the eight-wheel hub motor designed in this paper,the four-drive steering mechanism is usually used for coordinated steering.
Fig.4 is kinematics model diagram of four-drive mechanism steering.It can be seen that when the four-steering structure is used for coordinated steering,the center of AGV movement is on the geometric center of the AGV steering mechanism connection.

Fig.4 Kinematics model of four-drive mechanism steering
The turning radiusRand the steering angular velocityωof AGV can be given as
(9)
(10)
According to Eqs.(3) and (9),it can be seen that when the same steering angleθis reached,the turning radius of the four-steering mechanism coordinated steering is 1/2 of the steering of the two front wheels,the turning efficiency is higher.Therefore,the four-drive steering mechanism is usually used for coordinated steering during operation.
In this mode,the turning radius on the left and right sides can be given as
(11)
According to Eq.(11),the angle and speed of each steering mechanism in this movement mode can be given as
(12)
(13)
According to Eqs.(12) and (13),it can be seen that,in this mode,the front left and rear left steering mechanisms of AGV have equal speeds,and angles of rotation are equal,the front right and rear right steering mechanisms of AGV have equal speeds,and angles of rotation are equal.It is relatively simple to control the speed and angle of AGV.
The corresponding speed of each hub motor can be expressed as
(14)
2.2.3 Kinematics model of in-situ rotation
When the working conditions of the omnidirectional AGV require a small turning radius during operation,the AGV can perform in-situ zero-radius steering motion.In this mode,AGV rotates around the geometric center of the vehicle body (as shown in Fig.5).
The relationship between the rotation angle and speed of each steering mechanism can be given as
(15)
(16)
The linear speed of each hub motor can be expressed as
(17)
2.2.4 Kinematics model of crab movement
For special operations,AGV is unable to steer.The omnidirectional AGV can turn the steering mechanism.When the four steering mechanisms reach the same steering angle,the AGV can move along a specific angle with the same posture.Fig.6 shows the model diagram when the angle of each steering mechanism is 90°.
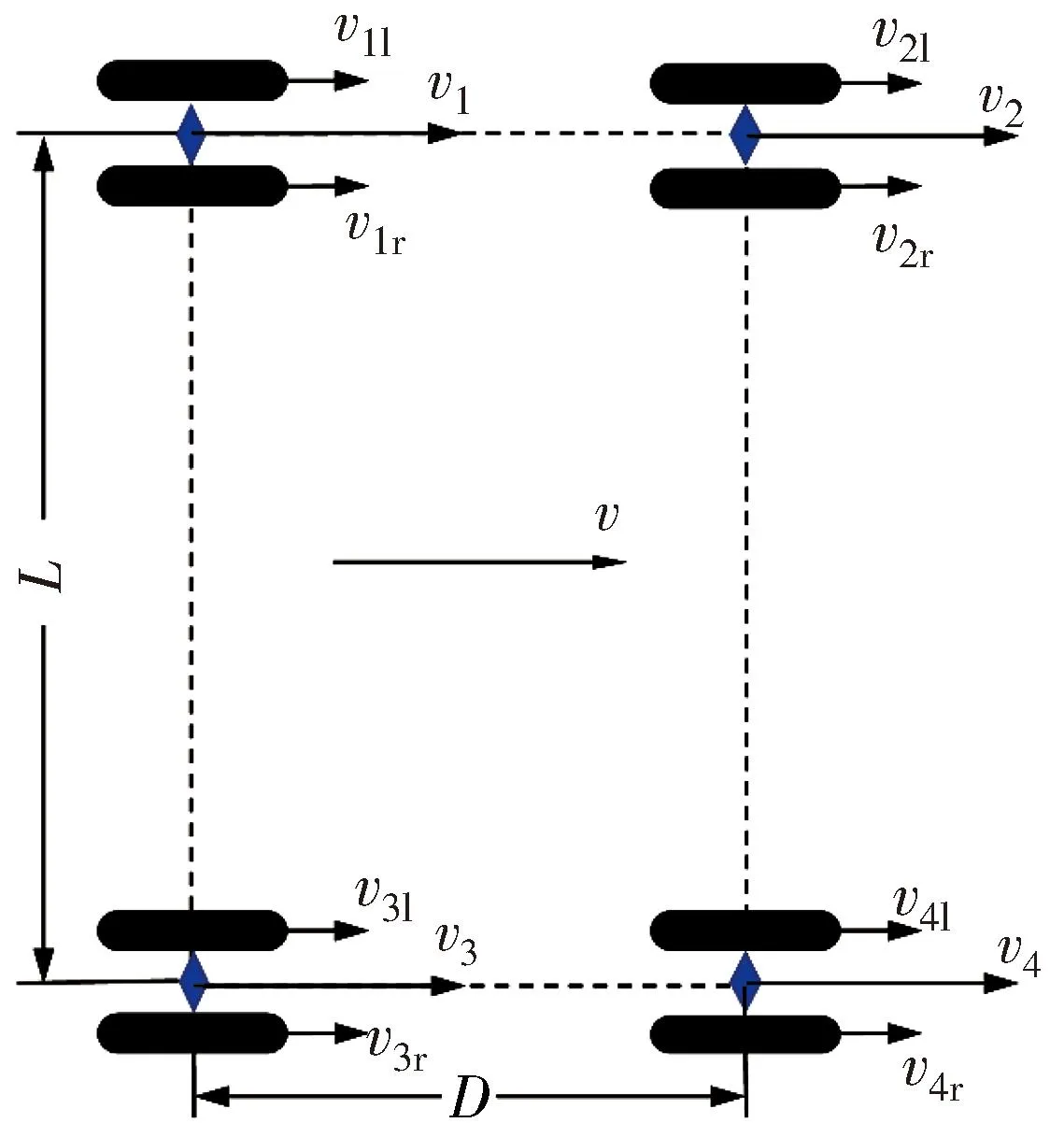
Fig.6 Kinematics model diagram of crab movement
In this mode,the steering angles of the AGV and the linear speed of the hub motor are the same.The omnidirectional AGV set up in this paper can meet the normal driving function under heavy load operation and has both functions of in-situ rotation and crab movement.Kinematics models under different steering modes are established to obtain the relationship between the steering angle of the steering mechanism and the speed of each wheel,and the motion path tracking control strategy of the omnidirectional AGV is studied in the four-wheel steering mode.
3 Control strategy
In the course of pathtracking,the omnidirectional AGV has a pose deviation between the motion path and the target path.Pose deviation can be divided into distance deviation and heading deviation.In order to quickly eliminate the deviation,a multivariable input fuzzy neural network PID control strategy is used to control and track the distance deviationedand heading deviationeθin the process of omnidirectional AGV path tracking and correct the deviation[22-23],and the conjugate gradient method (FR method) is used to optimize neural network weights[24].
Fig.7 is the fuzzy neural network PID control principle diagram with multi-variable input.
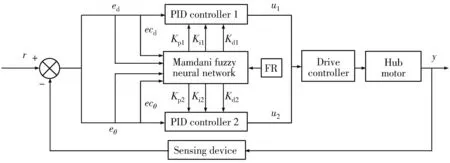
Fig.7 Fuzzy neural network PID control principle diagram with multi-variable input
3.1 Traditional PID control
Traditional PID control has good robustness and reliability,therefore it is widely used in industrial control.Its control algorithm can be expressed as
(18)
The controller mainly adjusts the three coefficients of proportionalKp,integralKi,and derivativeKd,so that the system can respond quickly.For a multivariable input system,e(k) is the input error of the system,which is the distance deviationedand the heading deviationeθ.
3.2 Fuzzy neural network PID control
The fuzzy neural network of the eight-wheel omnidirectional AGV is based on the Mamdani model.Fig.8 is the structure diagram with the distance deviationedas the input.When the heading deviationeθis the input,the structure is the same,which is a 5-layer structure of 2-14-49-49-3.
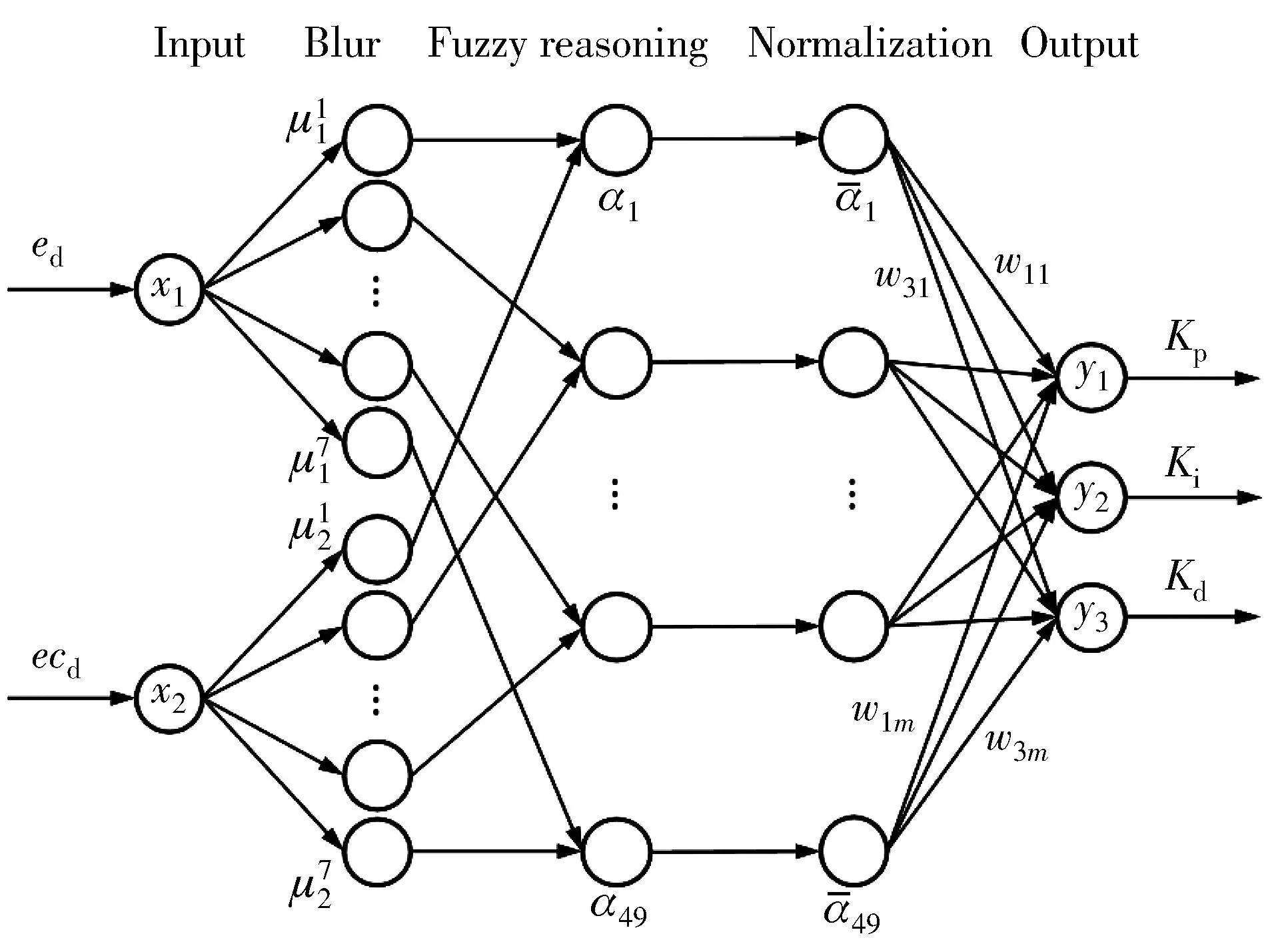
Fig.8 Mamdani type fuzzy neural network structure diagram
The first layer is the input layer of the fuzzy neural network.The number of nodes in this layer is 2,and its function is to receive the universe of distance deviationedand heading deviationeθof the inputxi,and pass it to the second layer.In order to ensure the stability of the controlled system,the domain of distance deviation is[-0.6 +0.6],the unit is m,and the quantization level is set to[-6 +6].The domain of heading deviation is[-45° +45 °],and the quantization level is set to[-6 +6].
The second layer is the fuzzification layer of the input variables of the fuzzy neural network,and each node represents a language variable.Distance deviationedand heading deviationeθcorrespond to seven blurs:PB (positive big),PM (positive middle),PS (positive small),Z (zero),NS (negative small),NM (negative middle),and NB (negative big).The language set has 14 nodes.The membership function adopts Gaussian function,and it can be described as
(19)
wherecijandσijare the center value and width corresponding to the fuzzy language of Gaussian function,i=1,2,j=1,2,3,…,7.
The third layer is the reasoning layer of the fuzzy neural network.The nodes in this layer correspond to the fuzzy inference rules one-to-one.The total number of nodes is 49.Its function is to match the antecedents of the fuzzy rules and calculate the applicability of each rule.In order to consider the distance deviation and heading deviation weight,the cumulative method is used instead of taking the small method.The equation can be shown as
(20)
wherej1=j2=1,2,3,…,7;j=1,2,3,…,49.
The fourth layer is the normalization layer of the fuzzy neural network with a total of 49 nodes,and the relationship between the input and output can be described by
(21)
wherej=1,2,3,…,49.
The fifth layer is the output layer of the fuzzy neural network.This layer mainly realizes the amount of clarity obtained by the anti-blur calculation,namely
(22)
wherei=1,2,3;wijis equivalent to the weight coefficient of the connection between the fourth layer and the fifth layer,and it is also the center value of the membership function of thejfuzzy rule language ofyi,the vector expression can be described as
(23)
where
(24)
3.3 FR learning algorithm
After the structure of the Mamdani type fuzzy neural network 2-14-49-49-3 is confirmed,its parameters need to be learned and trained,including the center valuecij,widthσijof the second-level membership function,and the connection weightwijbetween the fourth and fifth layers.The fuzzy segmentation of the input in this paper is determined in advance,therefore the center valuecijis-6,-4,-2,0,2,4,6.The widthσijis 2,only the weightwijneed to be trained.As a multi-layer feedforward network,the BP network error back propagation method is often used to learn the weightwijparameter,the essence is the gradient descent method and the equation can be described as
wn+1=wn+αngn=wn-αn∇f(wn),
(25)
wherewnis weight vector;αnis learning rate; ∇f(wn) is current gradient.
The gradient descent method has a simple algorithm,but convergence speed is slow,and the system performance cannot meet the requirements.The conjugate gradient method (i.e.,FR method) does not need to store the matrix in the calculation process,and the calculation amount is small.It has the advantages of faster convergence speed and quadratic termination.Therefore,the FR method is used to adjust and find the optimal weightwijto minimize the error cost functionEof the neural network.The error cost functionEcan be described as
(26)
whererjis the expected output;yjis the actual output of the neural network.
The conjugate gradient method is the same as the gradient descent method.The first step is to search in the negative gradient direction to find the most optimal weight,the gradient isd1=g1=-∇f(w1)=-∇E|w1.The second and subsequent search directions are conjugate to the current direction.The equations can be described as
wn+1=wn+αndn,
(27)
(28)
wherednis the search direction;βnis the gradient ratio which is expressed by the square ratio of the two gradient modes before and after; the gradient ratio expression is set as
(29)
In the process of searching weights in the conjugate gradient method,the first search direction is the negative direction,and the initial value of the weight isw1.Differentαnis adjusted to makewn+1the smallest.Each subsequent search direction is conjugated with the previous one,in order to make the algorithm converge,the search direction needs to be adjusted in real time.When ∇f(wn)Tdn≥0,dn=-∇f(wn),the new search direction is the gradient descent direction.Fig.9 shows the Mamdani type fuzzy neural network algorithm flow based on the FR method.
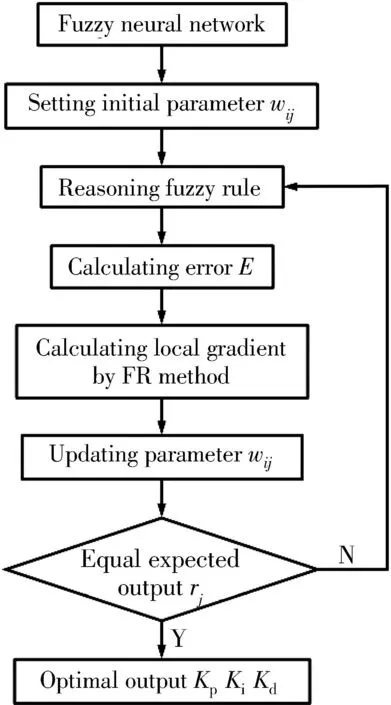
Fig.9 Flow chart of fuzzy neural network learning algorithm
4 Simulation and experiment
A 5-layer Mamdani type fuzzy neural network PID controller with a structure of 2-14-49-49-3 is used to track and correct the omnidirectional AGV path,and the fuzzy neural network is learned and trained based on the FR method.In order to verify the superiority of this algorithm in path tracking control,the unit step simulation experiment is performed in Simulink with the traditional PID control,the FNN-PID control not optimized by FR method,and FNN-PID control optimized by FR method.The feasibility and reliability of the proposed algorithm in AGV path tracking are verified.
4.1 Unit step simulation analysis

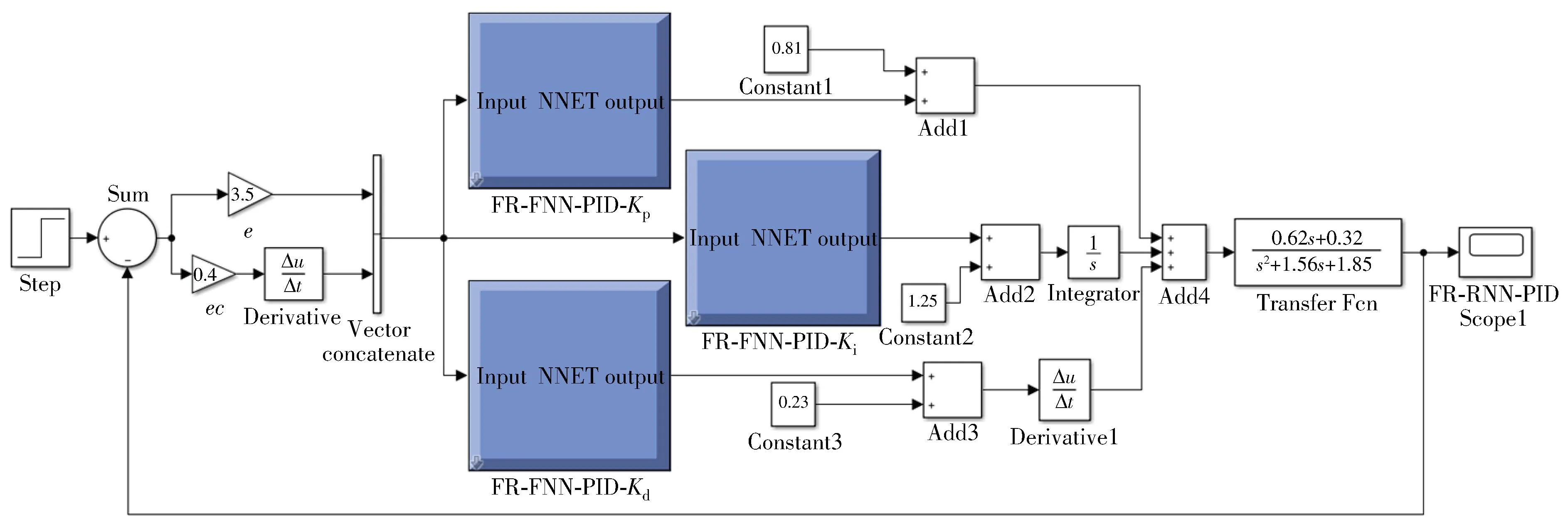
Fig.10 System simulation model under FR-FNN-PID control algorithm
In order to analyze the characteristics of the controlled object,a step response with an amplitude of 1 is given to the system.
Fig.11 is the unit step response diagram of the system under different control algorithms.It can be seen that the traditional PID controller has a fast response speed,but the overshoot is large and the system takes a long time to stabilize,and the overall performance is poor.Although the conventional fuzzy neural network PID controller (FNN-PID) has no overshoot and has good system stability,but the response speed of the system is too slow,which is not conducive to real-time path tracking adjustment.The fuzzy neural network PID controller (FR-FNN-PID) using the FR learning algorithm has greatly improved the response speed and stability.

Fig.11 Unit step response diagram of the system under different control algorithms
4.2 Experimental verification
In order to effectively verify the reliability and superiority of the proposed AGV motion control strategy in path tracking,path tracking experiment is carried out on the built omnidirectional AGV.The wheelbase of the AGV is 80 cm,and the left and right wheelbase is 60 cm.The path tracking is a semicircular path with a radius of 2 m,and in the initial state of the tracking experiment,the given AGV has a distance deviation of 20 cm and a heading deviation of 20°.The navigation method is magnetic navigation,the distance deviationedand the heading deviationeθfrom the target path in the course of the AGV path tracking and the data information of the driving track are collected by sensors.
Fig.12 is the experimental data of trajectory tracking and correction of AGV under different control strategies.It can be seen that under the traditional PID control strategy,the AGV can quickly adjust the pose error,on the contrary the path tracking shows a swing state,which is consistent with the large overshoot and unstable effect of the system during simulation.Under the fuzzy neural network PID control strategy,the AGV adjusts the pose error slowly,the correction process is long,and there is a large reverse error,while the later path tracking is smooth,which is consistent with the system’s failure to respond in time during the simulation.The fuzzy neural network PID control strategy trained by FR learning algorithm can quickly return to the target path in 2 s,the distance deviation and heading deviation are quickly eliminated and fluctuate in the range of 1 cm and 1°.Compared with other control strategies,the proposfed control strategy has good performance in path tracking and correction effect,this control strategy is improved to meet the requirements of use.

(a) Semicircle path tracking and deviation correction experiment results
5 Conclusions
A new type of omnidirectional AGV with large driving torque and good damping effect is designed based on the wheel hub motor.Four kinematic relations in different motion states are established,and the relationship between the rotation angle and speed of each mechanism is obtained.Aiming at the rapid and stable elimination of path deviations in the process of AGV path tracking,a fuzzy neural network PID control path tracking strategy based on FR learning algorithm is designed.Verified by simulation analysis and AGV experiment,the control strategy has good tracking and correction performance in AGV path tracking,meets the requirements of design,and has certain engineering application value.
 Journal of Measurement Science and Instrumentation2023年4期
Journal of Measurement Science and Instrumentation2023年4期
- Journal of Measurement Science and Instrumentation的其它文章
- Chaotic opposition initialization and average mutation update-based differential evolution
- Train driver fatigue detection based on facial multi-information fusion
- Improved target detection algorithm based on Faster-RCNN
- An improved algorithm for adapting YOLOv5 to helmet wearing and mask wearing detection applications
- A real-time laser stripe center extraction method for line-structured light system based on FPGA
- Electro-hydraulic servo force loading control based on improved nonlinear active disturbance rejection control
