水下声速场构建方法综述

黄威, 高凡, 王君婷, 徐天河

(1.中国海洋大学 信息科学与工程学部,山东 青岛 266100; 2.山东大学 空间科学研究院,山东 威海 264209)

水下综合定位、导航、授时与通信(positioning, navigation, timing and communication, PNTC)体系建设是我国十四五规划和2035年远景目标中实现国家信息化的重要内容,对于海洋灾害预警、水下救援、海洋资源勘探开发以及国防领海安全具有重大意义[1-2]。随着传感技术以及水下机器人技术的发展,海面跨介质通信浮标、深海潜标、海底信标、水下自主航行器(autonomous underwater vehicle, AUV)以及水下遥控机器人(remotely operated vehicle, ROV)等设备组成了水下信息感知与获取、目标识别与跟踪的多源、实时、立体观测网络,成为实现水下PNTC服务的重要手段。

水下PNTC服务体系建设离不开定位与通信两大重要技术基础,不仅水下蛙人、潜航器等用户设备需要精确的定位、导航、授时服务,海洋温度、盐度信息采集以及生物活动信息的感知也需要附带精确的定位信息才更能体现其应用价值;同时,感知与采集的信息还需要及时回传到地面信息处理中心加以利用,因此,如何提高系统通信效率,提高系统定位精度与实时性,长期以来受到国内外学者的广泛关注。

在水下环境中,声信号的衰减远小于无线电信号与光信号,更适合于远距离信息传递,因此成为水下PNTC系统的主要信号载体。然而,受到水下温度、盐度与静压力的影响,水声信号传播速度具有复杂的时空动态变化特性,导致信号传播路径会因斯涅尔效应发生弯曲,为水声指向性通信系统的波束能量高效利用以及水声定位、导航的高精度测距带来挑战[3]。如果能够获得区域声速分布,则可以根据射线跟踪理论[4-6]对信号传播轨迹进行跟踪与重构,促进PNTC服务体系的定位、测距、授时高精度以及通信高效性发展。因此,实时、准确的声速场构建十分重要。

1 水下声速场构建方法

水下声速分布具有动态时空差异性,在同尺度空间距离中,声速随深度的垂向变化幅度远大于水平方向变化幅度,因此声速剖面(sound speed profile, SSP)通常被用于描述小尺度区域中的声速场分布情况。目前,水下声速剖面的获取主要方法包括直接测量法和声速剖面反演方法。

1.1 直接测量法

人类对于声速测量的尝试可追溯到1827年的日内瓦湖实验,瑞士物理学家D. Colladon和法国数学家C. Sturm合作利用声管接收到了远处的潜水钟发出的响声[7]。日内瓦湖实验第1次测量出了声音在湖水中的传播速度,但是限于实验条件,没有能够获取声速随深度的变化情况。

随着电子仪器的发展,20世纪50年代出现了利用声脉冲信号进行声速直接测量的声速仪(sound velocity profiler, SVP),包括1953年Brown基于相位法研制的声速变化记录仪、1957年Greenspan和Tschiegg基于脉冲法研制的“环鸣式”SVP和1960年Scheffel基于共振法研制的低频SVP[8]。SVP可以进行测量声速绝对值,但是设备不易小型化,且不利于探究声速全球声速的时空变化规律,因此难以进行声速预报。

1960年,Wilson等总结出了较为准确的声速经验公式[9-10], 推动了水下传感设备的迅速发展,使得水下声速剖面可以利用温盐深剖面仪(conductivity, temperature, depth profiler, CTD)以及更加小型、便携的抛弃式温盐深剖面仪(expendable CTD, XCTD)等仪器设备[11]结合声速经验公式进行测量。除此之外,Leroy、Grosso、Medwin等分别提出了不同适用条件下的经验公式,常用声速经验公式及其适用范围列举如下。

1) W.D. Wilson精确公式[9]。

v=1 449.14+vt+vp+vs+vtpS
vt=4.572 1t-4.453 2×10-2t2-2.604×
10-4t3+7.985 1×10-6t4
vp=1.602 72×10-1p+1.026 8×10-5p2+
3.521 6×10-9p3-3.360 3×10-12p4
vs=1.397 99(S-35)+1.692 02×
10-3(S-35)2
vtpS=(S-35)(-1.124 4×10-2t+7.771 1×
10-7t2+7.701 6×10-5p-1.294 3×
10-7p2+3.158 0×10-8pt+1.579 0×
10-9pt2)+p(-1.860 7×10-4t+
7.481 2×10-6t2+4.528 3×10-8t3)+
p2(-2.529 4×10-7t+1.856 3×10-9t2)+
p3(-1.964 6×10-10t)

(1)

式中:t为温度,℃;S为盐度,‰;p为压强,kg/cm2。W.D. Wilson精确公式适用范围为:温度[-4 ℃, 30 ℃],盐度[0, 37‰],压强[0, 1 000 kg/cm2]。

2) Leroy经验公式[12]。

v=1 492.9+3(t-10)-0.006(t-10)2-

0.04(t-18)2+1.2(S-10)-

0.01(S-35)(T-18)+Z/61

(2)

式中:t为温度,℃;S为盐度,‰;Z为深度,m。Leroy经验公式适用范围为:温度[-2 ℃, 34 ℃],盐度[20‰, 42‰],深度不超过8 000 m。

3) Del Grosso经验公式[13]。

1974年,Del Grosso总结出高盐度环境条件下的声速经验公式,其适用范围为:温度[0, 30 ℃],盐度[30‰, 40‰],压强[0, 1 000 kg/cm2]。

4) Medwin经验公式[14]。

1975年,Medwin在Wilson精确公式的基础上提出了简化公式:

v=1 449.2+4.6t-0.055t2+0.000 29t3+

(1.34-0.01t)(S-35)+0.016Z

(3)

式中:t为温度,℃;S为盐度,‰;Z为深度,m。Medwin公式适用范围为:温度[0, 35 ℃],盐度[0, 45‰],深度[0, 1 000 m]。

5) Chen-Millero经验公式[15]。

1977年,Chen和Millero通过研究Wilson的测量数据,将1个大气压下的Wilson测量数据平移至更精确的声速测量数据,提出了Chen-Millero经验公式:

v=Cw(t,p)+A(t,p)S+B(t,p)S3/2+D(t,p)S2

(4)

式中:t为温度,℃;S为盐度,‰;p为压强,102kPa,Cw(t,p)表示纯水中的声速,参数A、B、C、D可通过文献[16]查表获取。Chen-Millero经验公式适用范围为:温度[0, 40 ℃]、盐度[5‰, 40‰]、压强[0, 100 000 kPa]。1994年,Millero和Li在Chen-Millero经验公式基础上针对低温区间进行更为精确的修正,提出Chen-Millero-Li公式[17],被联合国教科文组织(United Nations Educational, Scientific and Cultural Organization, UNESCO)推荐为国际标准水下声速计算公式。

6) Coppens经验公式[18]。

1981年,Coppens对Del Grosso公式在高盐、低盐和低温范围进行外推,提出了Coppens经验公式,其适用范围为:温度[0, 35 ℃],盐度[0, 45‰], 深度[0, 4 000 m]。

在声速直接测量方法中,SVP可以进行声速绝对值测量,因此通常作为区域声速分布的标准,而基于CTD、XCTD的声速测量方式更加灵活、便携,但是其精度不如SVP,并且在不同环境有不同的适用经验公式。周丰年[19]从多波束测深系统最优声速公式确定的角度研究了主流声速经验公式的适用范围,陈长安[20]则利用中国南海的SVP测量数据为标准,通过CTD海试数据对主流声速经验公式的适用范围进行了比较分析,并给出了选择策略参考:在河流、湖泊、河口海岸及大陆架海域使用Chen-Millero-Li公式最优;在深海中Del Grosso公式和Coppens公式较优;Wilson公式由于最早提出,在教科书中被广泛提及,稳定性较好,但在低盐范围外推适用性不足。

CTD仪器设备得益于传感器体积小、操作简单、灵活、便捷的优势,其在20世纪50年代以来得到了快速发展。美国、意大利、加拿大、德国、日本等发达国家在CTD测量方面起步早,经过数十年的发展,技术长期处于世界领先地位,知名商用CTD产品主要有美国Sea Bird公司的“海鸟”——SBE系列CTD[21],美国YSI公司的SonTek CastAway CTD[22],意大利Idronaut公司的Ocean Seven (OS) 300系列CTD[23],加拿大RBR公司的RBR系列CTD[24],德国Sea &Sun Technology (SST)公司的CTD探测仪[25];日本则更专注于小型便携式产品研发,例如tsurumi-seiki (TSK)公司生产的TSK系列XCTD产品[26]。

我国CTD设备研制起步较晚,经过多年发展,仪器可靠性、稳定性大幅度提升,形成了船载、固定平台、水下移动平台等30余型全自主化的技术产品。国家海洋技术中心是国内最早开展CTD技术研究的单位,于2018年启动了全海深CTD研制工作,并于2020年开始逐步形成Ocean Sensor Technology (OST)系列产品,在温度、盐度测量方面达到了国际先进水平[27]。虽然我国温盐深测量技术取得了很大突破,但由于压力传感器耐压技术的不足,测量深度范围相比于顶尖商用CTD仍有一定差距。部分商用CTD和XCTD如图1所示。

图1 CTD与XCTD产品Fig.1 Products of CTD and XCTD

利用CTD(或SVP)进行声速剖面测量的优势在于数值测量结果准确,深度分辨率高,但由于测量需借助图2(a)所示的船载拖体方式停船执行,测量周期长,严重影响了作业效率。例如,当缆绳下放与回收速度为50 m/min时,测量2 000 m深的声速剖面需要80 min。相比较而言,XCTD测量时可以在海面平台保持航行(5 kn以内)时同步测量,探头依靠重力下落,通过铜丝回传数据,最后抛弃探头而无需回收,故不影响作业效率。同时,XCTD的便携性使其可搭载于无人机或无人潜航器等自动化平台[11,28-29],对于2 000 m深的声速剖面测量只需要大约20 min,因此测量声速剖面的实时性更高。XCTD的不足之处在于受到传感器耐压性能限制,其深度覆盖范围通常不超过2 000 m。图2(b)给出了XCTD进行声速剖面测量的示意图。

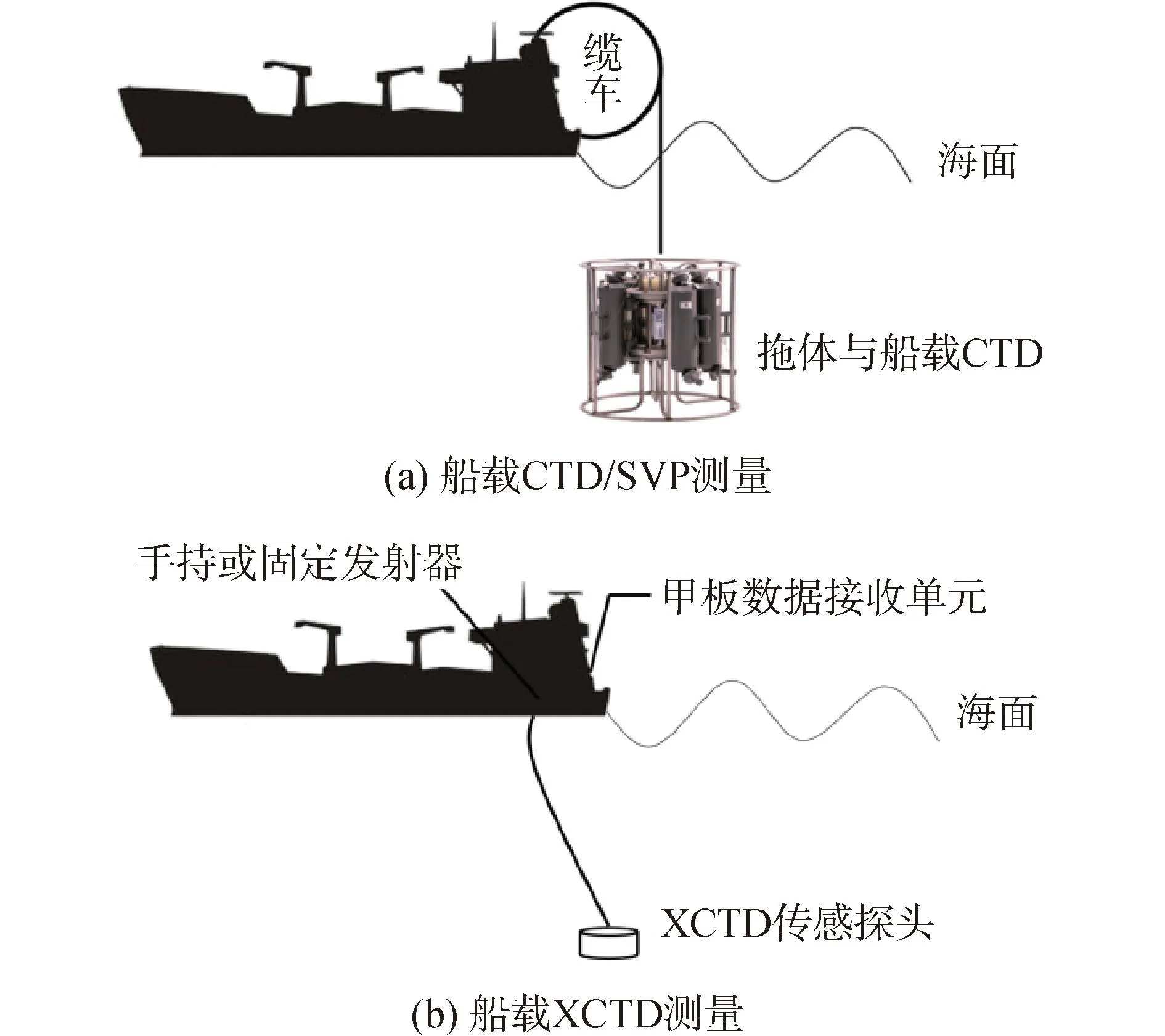
图2 基于CTD/XCTD的舰船SSP测量Fig.2 SSP measurement with CTD/XCTD on ships

为了能够利用XCTD测量的部分海深声速数据对全海深声速剖面进行重构,成芳等[30]提出了一种陆缘深水区声速剖面的正交经验函数(orthogonal empirical function, EOF)分解延拓方法,能够有效实现声速剖面低精度损失延拓,但是该方法要求先验数据信息覆盖范围超过声道轴深度,因此应用具有局限性。受到上述方法的启发,徐天河等[31]提出一种基于EOF分解的声速剖面延拓方法及系统,能够有效实现全球海洋地区的XCTD测量数据延拓。典型商用CTD性能对比如表1所示。

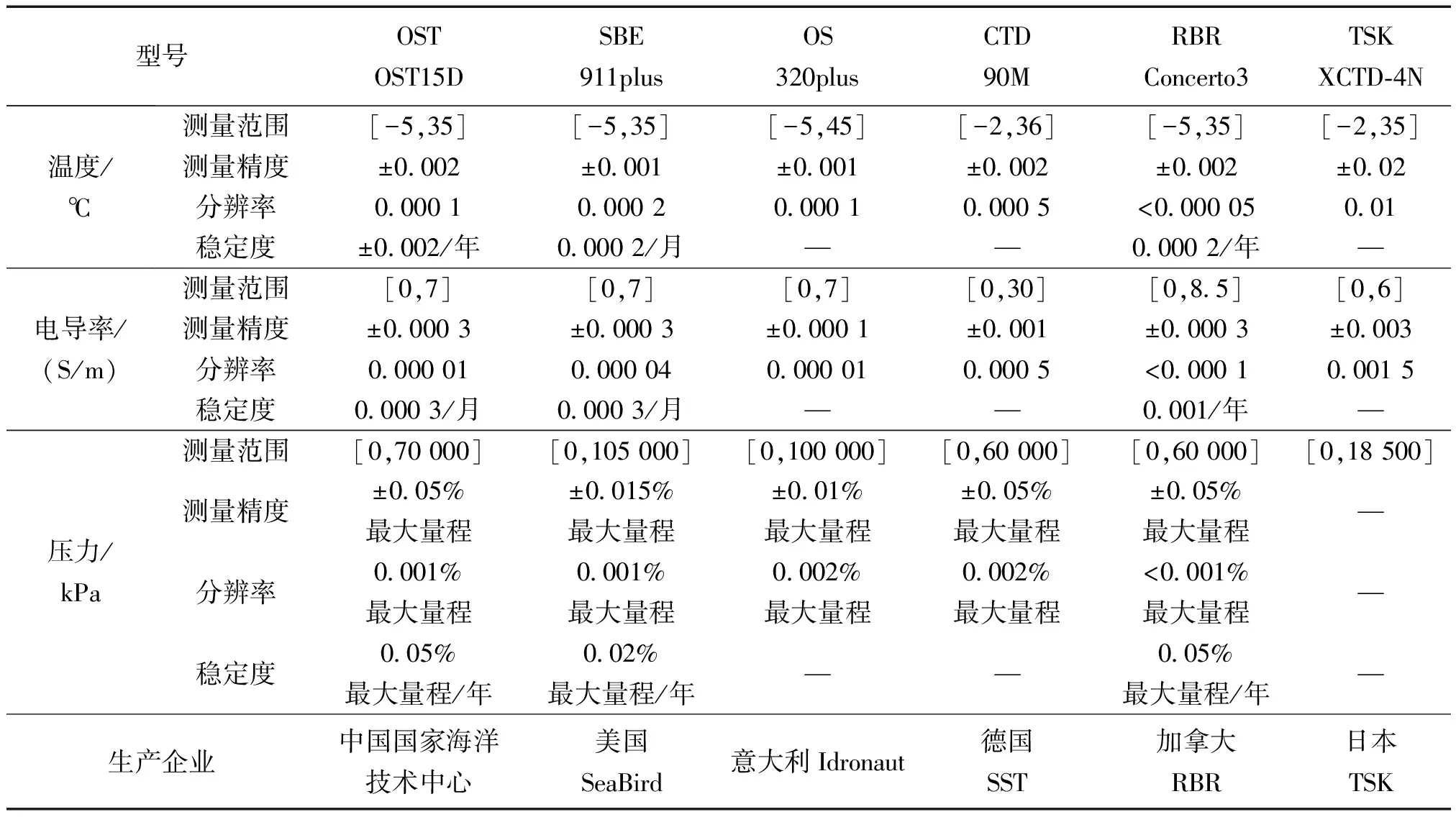
表1 典型商用CTD性能对比Table 1 Performance comparison of typical commercial CTDs

随着人类对海洋测绘信息需求增加,低成本、大范围海洋测绘作业开始受到关注。21世纪初期,加拿大BOT公司首先研制出了走航式多参数剖面测量系统(moving vessel profiler, MVP),形成了MVP30、MVP100、MVP200、MVP300[32]和MVP800系列产品。MVP系统主要组成包括拖鱼、数据采集单元、绞车、液压系统以及远程控制系统等,其中拖鱼不仅可以搭载CTD,还能同时搭载叶绿素计、溶氧传感器等多种功能海洋测绘设备。

我国的MVP系统研制也在同一时期开展。2005年,国家海洋局第一海洋研究所首次研制了国产MVP系统[33],通过0～200 m深度实验验证,表明产品处于当时国际先进水平。此后,国产MVP系统逐步更新迭代,如杭州应用声学研究所于2010年研制CZT1-3A型MVP系统[34],中国科学院海洋研究所联合上海劳雷仪器系统有限公司于2016年研制的MVP 3400系统[35],其中MVP3400在停船作业时最大覆盖深度为3 400 m,作业周期70 min,在12 kn航速时作业深度可达300 m,周期13 min。

1.2 声速反演法

声速分布的时间、空间的不均匀分布,导致了水下声场的动态变化性,1979年,Munk等[4-6]将地球物理反演的方法引入到海洋物理中,创造性地提出了海洋声层析的概念,包括正演问题、观测技术及反演问题。正演问题主要研究水声传播模型,在给定信源与信宿拓扑情况下预测理论声场;观测技术关注于声场的准确测量,根据观测数据获取信号传播属性信息;反演问题则通过声场的观测数据,如信号接收强度、信号传播时间等,通过优化算法估计海洋物理参数。

声速剖面反演是海洋声层析的一种,它通过海洋声场观测数据,反推目标时空区间的声速分布情况。1981年,伍兹霍尔海洋研究所联合麻省理工学院等单位在墨西哥湾流试验海域采用发声机、接收机、声学导航系统等设备进行海上实验,通过声层析方法,测得区域声速剖面,对声速反演方法的可行性进行了实践验证[36]。相比于使用CTD、SVP或XCTD等设备仪器的直接测量方法,声速反演方法采用预布设水下信标设备进行声场测量,其响应周期更短,更符合水下灾害预警以及国防安全等领域的实时性需求。

2 水下声速剖面反演技术

近30年来,国内外学者在声速剖面反演方法方面进行了许多研究工作,先后提出了匹配场处理、压缩感知、深度学习等多种方法框架。

2.1 匹配场处理声速剖面反演

1991年,美国海军实验室将匹配场处理方法[37]应用到海洋声层析中,建立了长期以来声速剖面反演的主流框架,如图3所示。

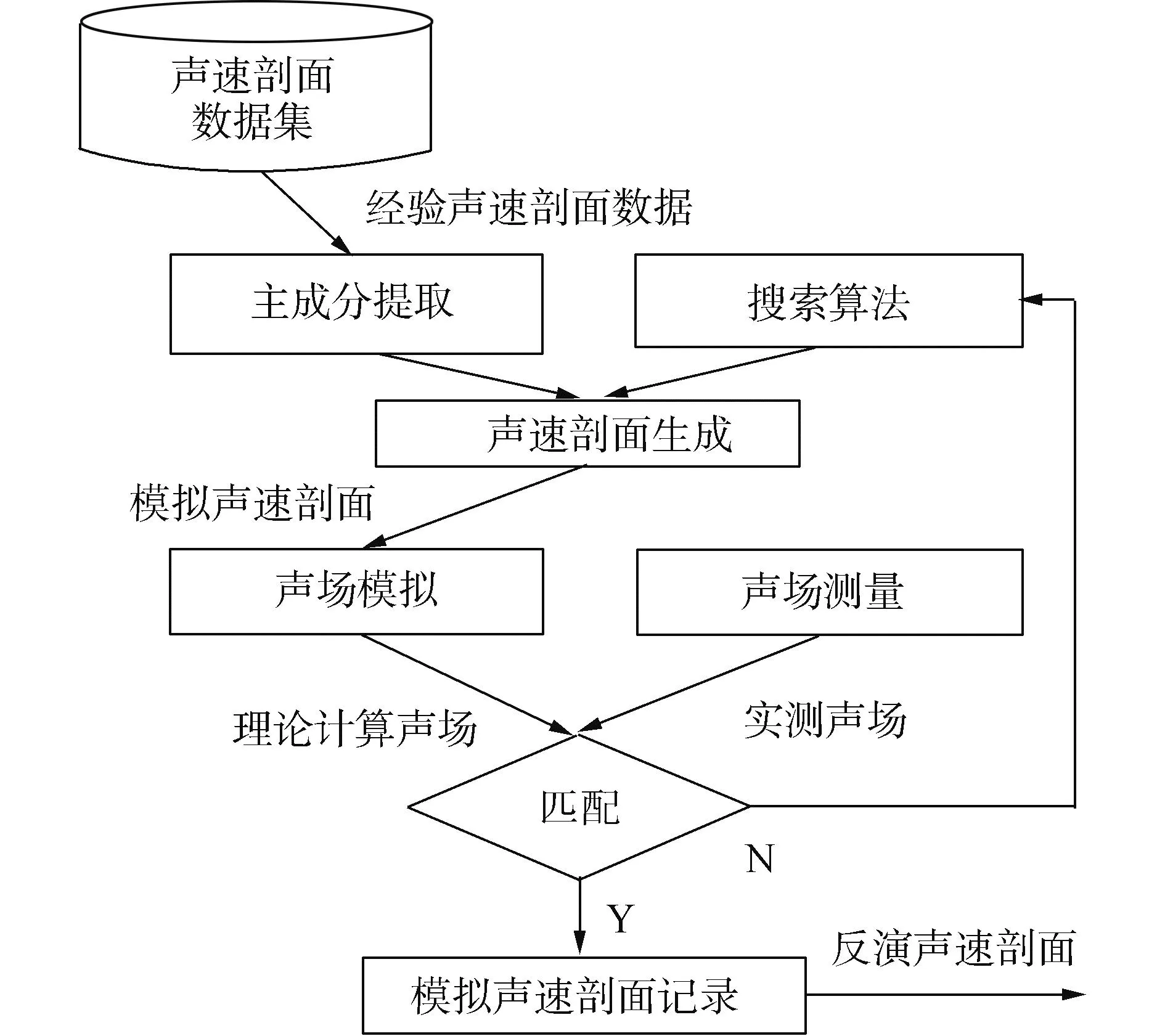
图3 匹配场处理声速场构建框架Fig.3 SSP construction framework by matching field processing

该方法框架中首先对经验声速剖面进行主成分分析,提取目标时空区间经验声速分布的主成分特征;其次采用搜索算法对主成分系数进行搜索,生成候选声速分布;然后对于每一组候选声速分布,根据射线理论或简正波理论计算理论上的声场分布;最后通过模拟计算声场与海洋实际声场测量值进行匹配,最优声场匹配结果所对应的声速分布即是最终的声速反演结果。匹配场处理方法回避了建立声场信息到声速分布的反向映射关系的难题,为声速场构建提供了有效实现途径。

2.1.1 基于EOF的匹配场处理方法

匹配场处理中需要对经验声速剖面数据进行主成分分析来获取其分布特征,美国海军实验室Tolstoy于1991年将基于EOF进行主成分分析的匹配场方法用于声速剖面反演[37],并采用格点遍历方法搜索匹配项,其过程计算复杂度高,反演时效性亟需改进。

EOF是一种主成分分析方法,通过分析矩阵数据中的结构特征,来提取主要数据特征量。对于给定的声速反演任务,历史经验声速剖面集合表示为:

Sp={Sp,1,Sp,2,…,Sp,i},i=1,2,…,I

(5)

式中Sp,i={(d1,sp,i,1),(d2,sp,i,2),…,(di,sp,i,j)},j=1,2,…,J为第i个样本,di为第j个深度层的深度值,sp,i,j为对应声速值。根据历史声速剖面样本计算平均声速剖面:

(6)

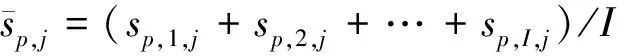
(7)

基于残差矩阵,可得到协方差矩阵:

(8)

进一步有正交经验函数关系式:

CS×U=U×Λ

(9)

式中U=[u1u2…um],m=1,2,…,M为J×M阶矩阵,每一个元素为一个特征向量,Λ是M阶对角矩阵,对角元素为特征向量对应的特征值大小,表明特征向量对于重构该地区声速剖面分布的重要性。

(10)

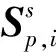
(11)

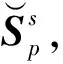
国内学者在基于EOF匹配场声速场构建方面也取得了许多重要成果。为了提高声速反演精度,西北工业大学张忠兵[38]针对匹配场处理容易受到海底参数失配影响的问题,于2002年提出匹配波束反演方法,通过波束传播路径控制,减小海底反射次数,一定程度上减小了反演精度对海底参数的依赖程度。哈尔滨工程大学张维[39-40]研究了不平整海底反射时的传播规律,于2013年提出一种三维空间特征声线搜索和传播计算模型,探讨了海底深度,声源位置和基阵倾斜等参数失配对声速剖面反演性能的影响。

为了提高匹配场处理中匹配特征项的搜索速度,2017年,哈尔滨工程大学郑广赢[41]提出微扰法改进算法,将声速剖面反演由非线性优化转化为线性方程组的形式,在降低部分精度的条件下,提高反演时效性。部分研究者在匹配场处理中引入启发式算法来加快反演过程,如粒子群算法(particle swarm optimization,PSO)[39-40],模拟退火算法[42](simulated annealing, SA),遗传算法[43-44](genetic algorithm,GA)。与文献[37]中的格点遍历搜索方式相比,启发式算法加快了声速剖面特征向量的主成分系数搜索过程,但是启发式算法核心是基于蒙特卡洛思想,需要设置足够多的粒子数(如粒子群算法)或种群个数(如遗传算法)来保障最优或次优匹配的搜索概率,因此仍具有高额的计算时间复杂度。

不同于传统的主动声呐通信方式,浙江大学徐文教授团队于2016年提出一种以AUV辐射噪声作为声源进行匹配场声速反演的方法,重点研究并解决了移动声源在存在多普勒干扰下的匹配场声速反演问题[45]。

2.1.2 基于字典学习的匹配场处理方法

美国加州大学圣地亚哥分校Bianco于2017年提出了一种基于字典学习的声速剖面反演方法[46-47],其重点关注问题在于声速剖面的稀疏表达,采用字典学习替代EOF方法,字典学习通过奇异值分解(singular value decomposition, SVD)与k-means结合的K-SVD算法实现。SVD算法对经验声速剖面进行稀疏表达,任意样本可表示为在平均声速剖面分布的基础上加上字典稀疏向量的线性组合:

(12)

式中:Q为声速剖面稀疏字典,若声速剖面声速采样点数为J,则Q为K×J阶矩阵,通常K≪J;qi为K×1系数向量。

字典学习所构建的字典无需相互正交,可有效提高特征向量对声速剖面主成分表达效率,减小特征向量与系数的数量,但该方法仍然属于匹配场处理的范畴,匹配项的高搜索复杂度仍未得到解决。

2.2 压缩感知声速剖面反演

美国加州大学圣地亚哥分校Bianco[48]和韩国首尔大学Choo[49]分别于2016年和2018年提出结合EOF分解的压缩感知声速反演的方法,分别利用信号传播强度和信号传播时间,通过建立压缩感知字典,采用最小二乘法求解超定问题来描述稀疏声速扰动对于声场的影响,压缩感知声速场构建框架如图4所示。

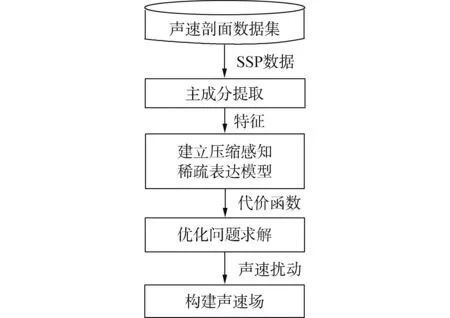
图4 压缩感知声速场构建框架Fig.4 SSP construction framework by compressive sensing

压缩感知方法中的字典构建不同于字典学习匹配场处理中的字典构建,后者的字典是对区域经验声速剖面分布的稀疏主成分表达,而压缩感知方法中的字典构建除了包含上述部分外,另一部分建立了声速扰动到声场分布的映射关系。

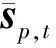
(13)

式中:ns为观测噪声,g(·)为声速剖面分布到声场分布的映射函数,对于简正波理论,式(13)可得到接收信号强度信息,对于射线理论,式(13)可得到信号传播时间信息。

由于g(·)通常为非线性函数,难以直接求解,压缩感知理论在声速剖面的微小变动条件下(即较小的q值空间),对式(13)进行泰勒级数展开并保存一阶泰勒展开式,得到估计声场:

(14)

则目标函数为:

(15)

式中:|q|1为正则化项;μ为正则化参数。目标函数可以利用CVX工具[48-49]或正交匹配追踪(orthogonal matching pursuit, OMP)进行求解。

压缩感知方法中由于主成分系数可以采用较少次的最小二乘迭代计算获得,因此其反演实时性相比于匹配场处理有较大提升,但是最优参数的迭代求解使其反演阶段实时性弱于神经网络声速场构建模型;此外,其字典建立过程采取了一阶泰勒展开进行线性化近似,反演精度有所牺牲。

2.3 深度学习声速剖面反演

2.3.1 基于声场观测数据的神经网络声速剖面反演

近年来,机器学习在图像识别、数值预报等多领域回归与分类问题中得到了广泛应用,得益于其具有拟合复杂非线性函数的能力,十分适合解决由声场分布反演声速分布的问题。1995年,美国军事海洋中心Stephan建立了利用人工神经网络(artificial neural network, ANN)进行声速场反演的框架[50],如图5所示。

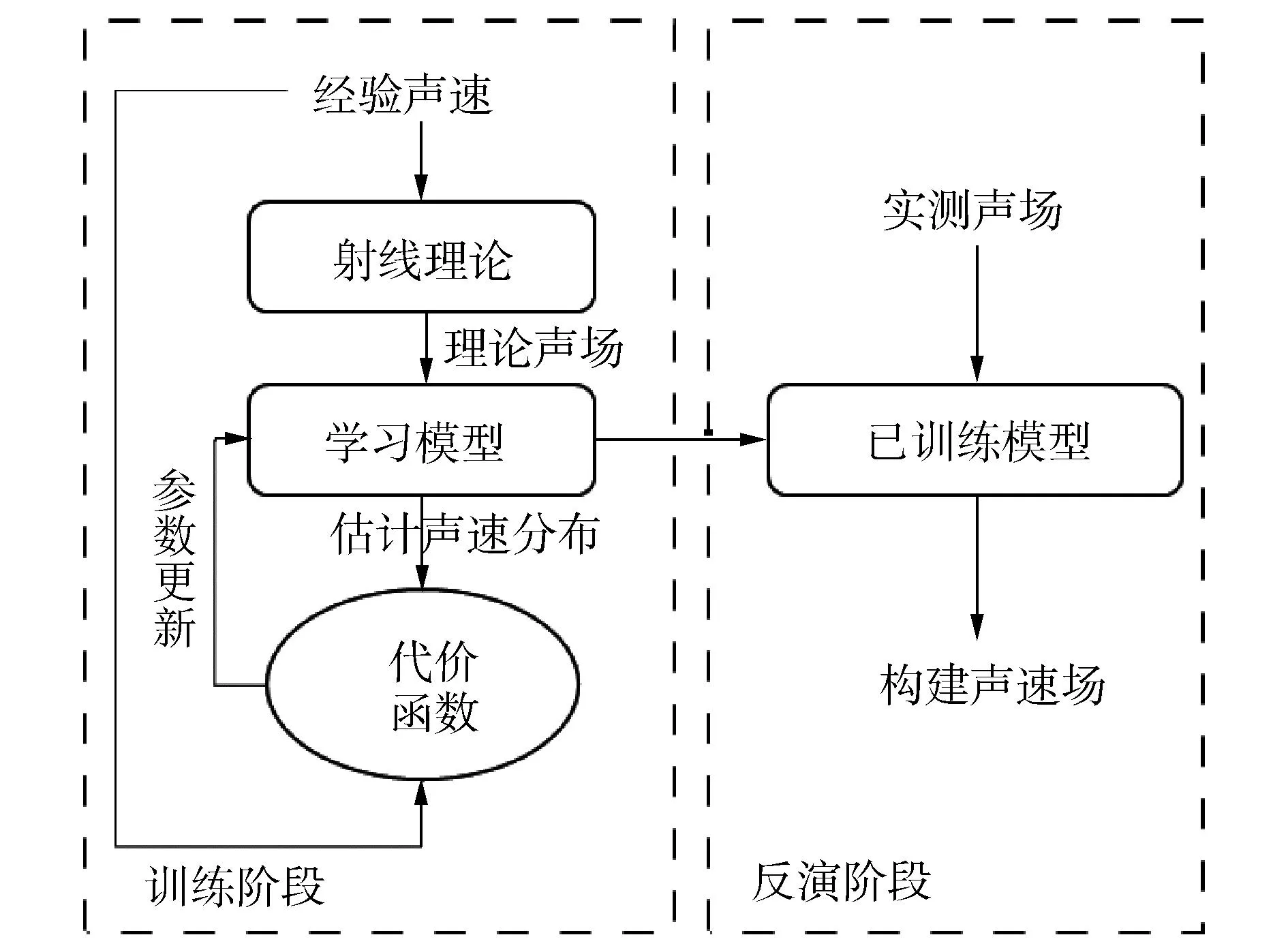
图5 深度神经网络声速场构建框架Fig.5 SSP construction framework by deep neural networks

深度学习ANN网络进行声速场构建主流思想是通过挖掘声场数据中隐含的声速分布信息来反演声速场,对于历史经验声速剖面样本,在已知信源和信宿空间拓扑关系的条件下,通过简正波理论、射线理论或抛物线方程模型进行声场模拟,用于作为模型输入数据,以声速剖面估计值作为输出;同时以当前历史经验声速剖面样本作为输出标注数据,建立代价函数,调整模型参数,建立声场到声速场的映射关系,完成模型训练阶段。在反演阶段,输入实时测量声场信息,即可构建出目标区域声速场。

声速分布具有时空差异性,而深度学习ANN网络声速场构建模型的优点在于模型建立时,可以为不同的时空区间预设定专用模型,并离线预先完成模型训练,在模型收敛后,对于输入声场数据,仅需要一轮正向迭代矩阵运算,即可获得声速场构建结果,因此相比于匹配场处理与压缩感知声速剖面反演方法,其反演阶段具有显著的实时性优势。但是ANN模型用于声速场构建时也面临着两方面重要挑战,一方面,水下声场测量不可避免受到噪声、多径效应等水下复杂环境耦合干扰,会降低模型对于声速场构建精度;另一方面,ANN模型训练需要大量历史经验声速剖面作为参考数据样本,由于经验声速剖面数据通常由CTD或SVP等仪器采集获得,成本高,因此许多海洋时空区域面临训练样本数据不足的问题,容易导致模型因过拟合而精度性能降低。

为了提高深度学习声速场构建模型对于声场测量噪声的抗干扰能力,本文作者于2021年提出一种自编码特征映射神经网络(auto-encoding feature-mapping neural network, AEFMNN)结构[51],如图6所示。通过自编码网络对含噪干扰声场进行去噪重构,提取鲁棒性更强的隐含特征,再由特征映射网络建立隐含特征到声速剖面分布的映射关系,有效提高了神经网络模型构建声速场的抗干扰能力。

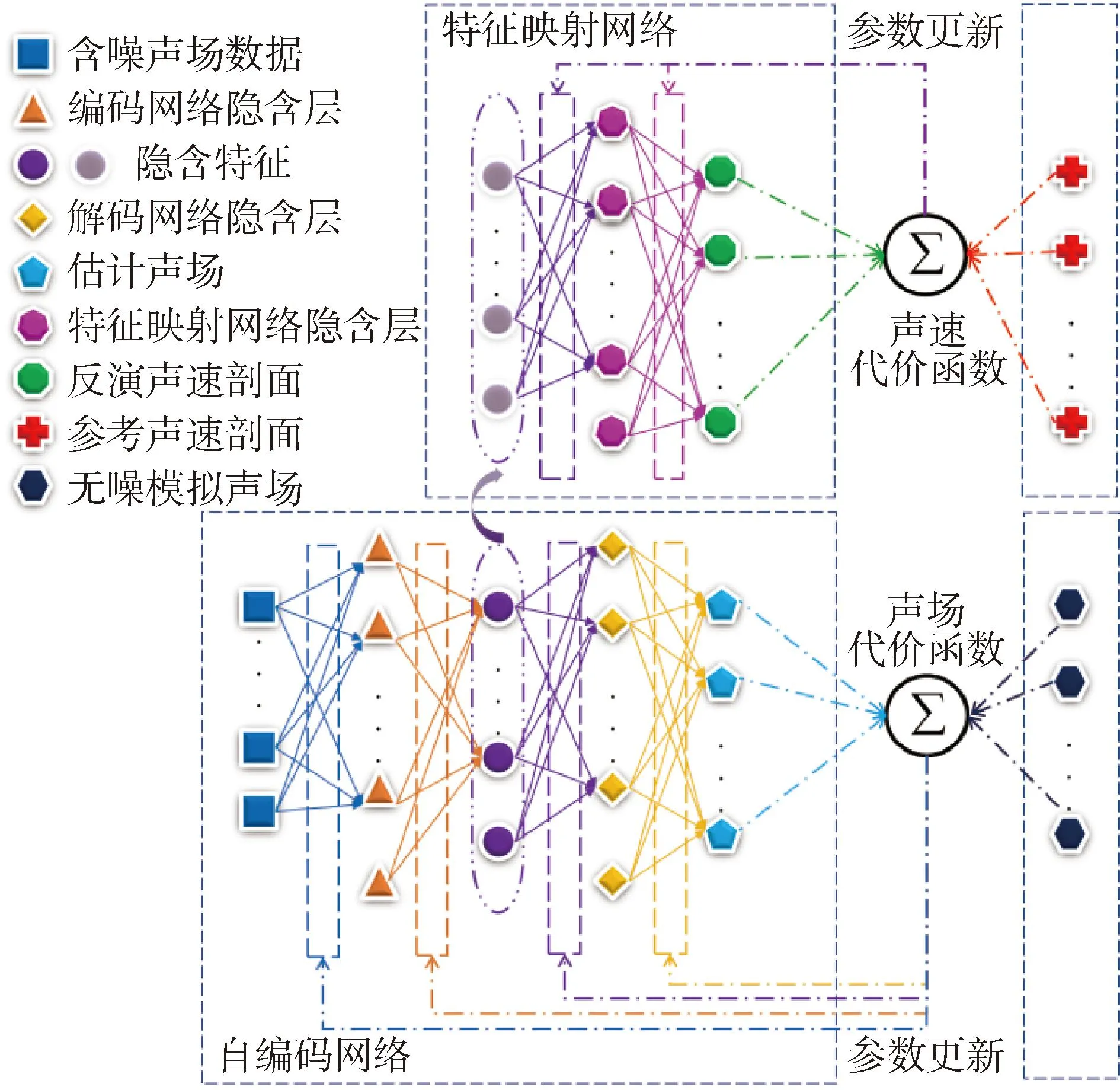
图6 自编码映射神经网络结构Fig.6 Structure of auto-encoding feature-mapping neural network (AEFMNN)

为了应对小样本场景下的模型过拟合问题,作者在文献[50]的基础上,提出一种智能扩充数据集辅助模型训练的ANN声速场构建方法[52]。该方法首先对已有参考样本进行特征点提取,然后根据所提取特征点在声速-深度二维平面取值区间生成新的声速剖面样本来扩充参考样本数据集(扩充样本不超过总样本30%),一定程度上缓解了参考样本数据不足的情况,但是仍然对原始参考样本数据量基数有一定要求。

为了更有效地应对小样本场景过拟合效应,2021年,文献[53-54]提出一种任务驱动的元学习(task-driven meta learning, TDML)声速场构建框架,框架结构如图7所示。该方法建立多个基元学习器、一个全局学习器以及按需设定的任务学习器,其核心思想是通过多个基元学习器对不同时空区域、不同类型的声速剖面进行同时学习,获取声速剖面分布的公共特征,并将其传递给任务学习器,使得任务学习器能够利用少量样本、少次训练即可实现模型收敛,保持模型对于输入数据的敏感性,从而提高其应对过拟合的能力。

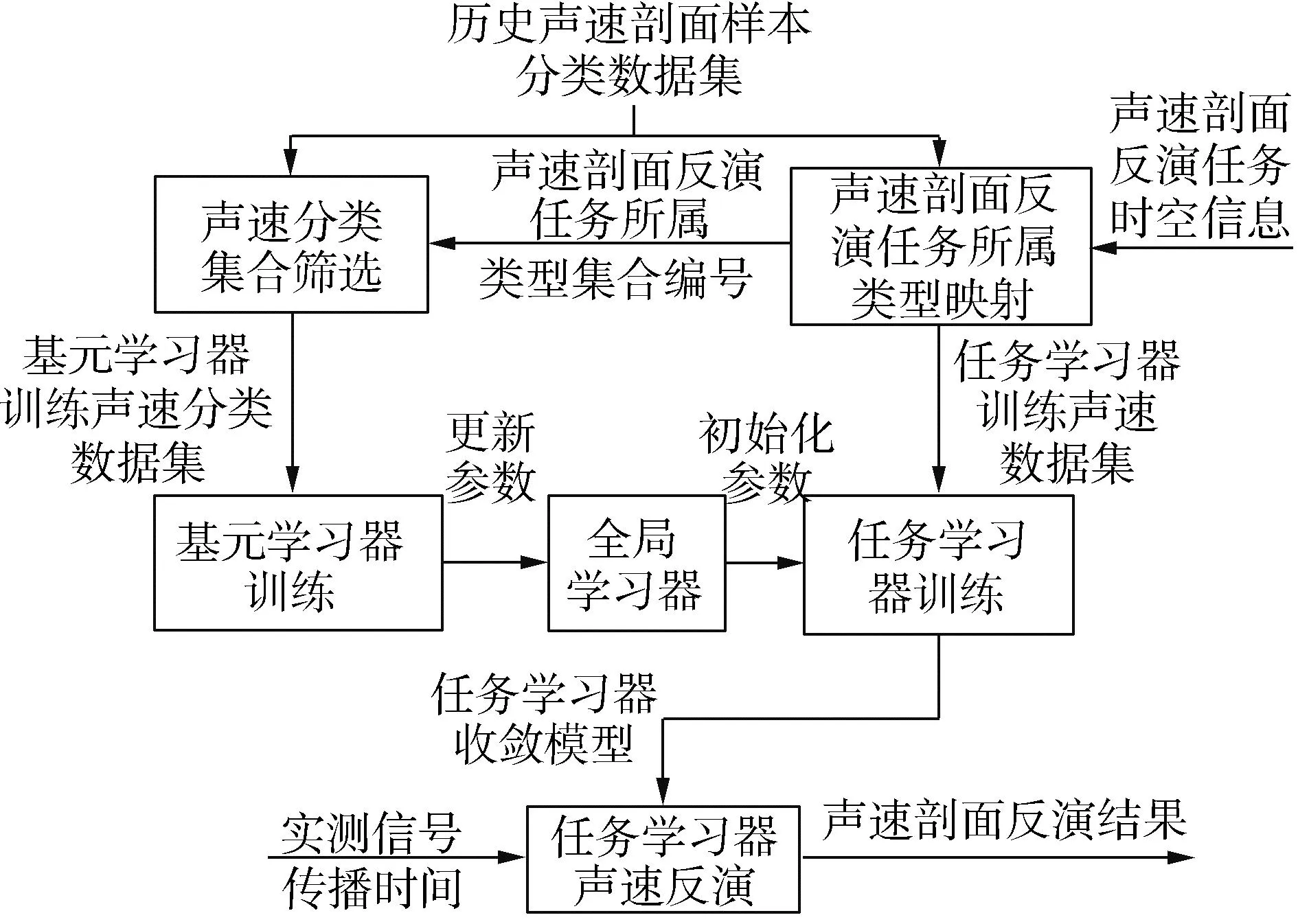
图7 元学习声速场构建框架Fig.7 TDML framework for SSP inversion

TDML的模型训练方式如图8所示,其中在元模型训练阶段,每一轮参数更新时,从A个声速剖面类型集合中随机挑选K个,逐一分配给K个基元学习器,每个基元学习器利用N个样本进行训练,1个样本进行测试,这种训练方式称为K-way N-shot。

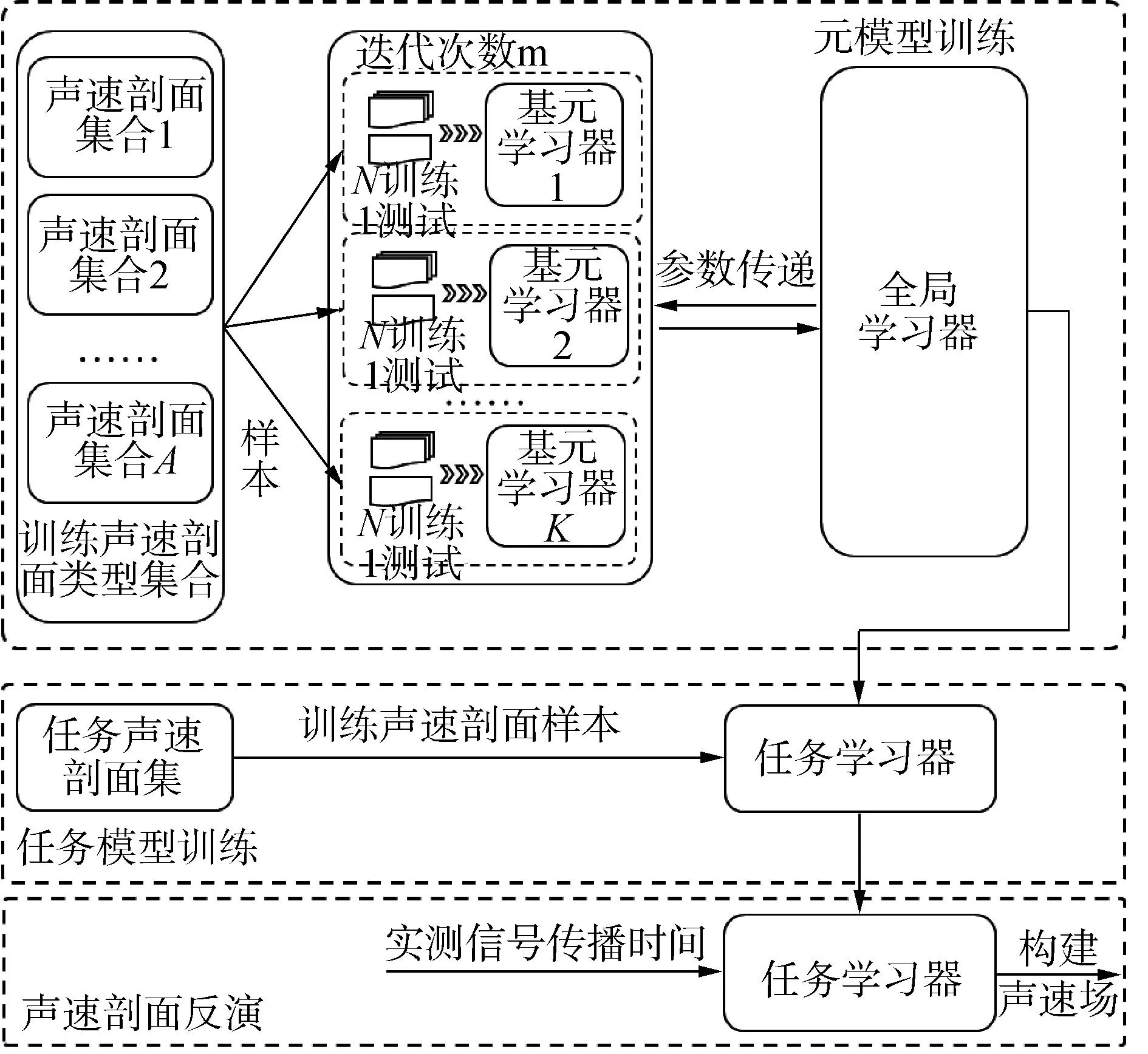
图8 元学习声速场构建模型Fig.8 TDML model for SSP inversion

上述ANN、AEFMNN、TDML声速场构建方法都是利用神经网络模型建立声场到声速分布的映射关系,能够根据实时声场输入数据快速估计声速剖面分布情况。由于设备研发经济成本以及覆盖范围受限等原因,这些方法和传统匹配场处理、压缩感知方法一样,对于声场数据的需求在空间上限制了其应用范围。

2.3.2 无声场观测数据的神经网络声速场构建

为了在无声场观测数据获取条件的时空区间进行声速场构建,文献[51]提供了一种利用不同地区多基站群进行大尺度区域三维声速场构建的策略。文献[51]的应用场景针对于已经分布式布设的海底观测系统,空间方位相对集中的多个海面或海底声基站对组成一个基站群(内部可互相通信),通过在每一个基站群进行声场测量,反演该基站群地区声速剖面,继而获得多个基站群地区声速剖面,然后经过插值拟合处理,最终获得基站群闭合区域内的声速场估计结果,但其本质上仍没有降低设备研发成本。

2020年,山东大学徐天河等[55-56]提出了一种基于径向基函数(radial basis function, RBF)神经网络的声速剖面预报方法,模型结构如图9所示。该方法设置温度、盐度场构建网络和声速场构建网络,首先利用历史温度、盐度剖面及其采样时的经度、纬度、深度信息,对目标区域的平均温度、盐度场进行构建,为声速场构建网络提供约束;然后利用历史声速剖面及其采样时的经度、纬度、深度信息进行目标区域的平均声速场构建。RBF方法无需现场实测声场观测数据,但是模型构建结果趋近于区域样本均值,难以精确描述声速剖面的时间、空间分布变化。

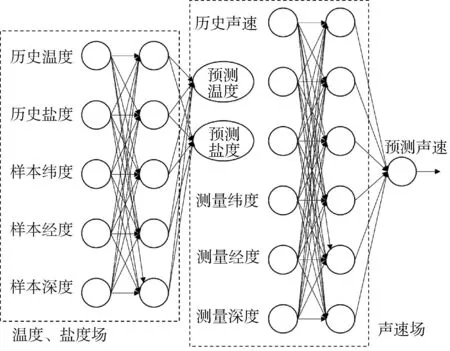
图9 RBF声速场构建模型Fig.9 RBF-based model for SSP Construction.

山东科技大学李倩倩于2022年提出一种基于自组织映射(self-organizing map, SOM)神经网络的全海深声速剖面反演方法[57],其模型结构如图10所示。该方法充分利用了全球卫星遥感系统的海表温度测量数据、历史声速剖面数据,并以可选形式加入海表声速测量结果,为无声场观测数据情况下的声速场构建提供了可行的解决方案,相比于基于径向基函数神经网络的声速剖面预报方法,能够对不同空间声速分布进行构建,更好体现声速分布的空间差异性,但由于模型依赖于海表温度和声速数据,无法充分描绘季节跃变层声速分布情况,其全海深声速剖面构建精度仍有很大提升空间。

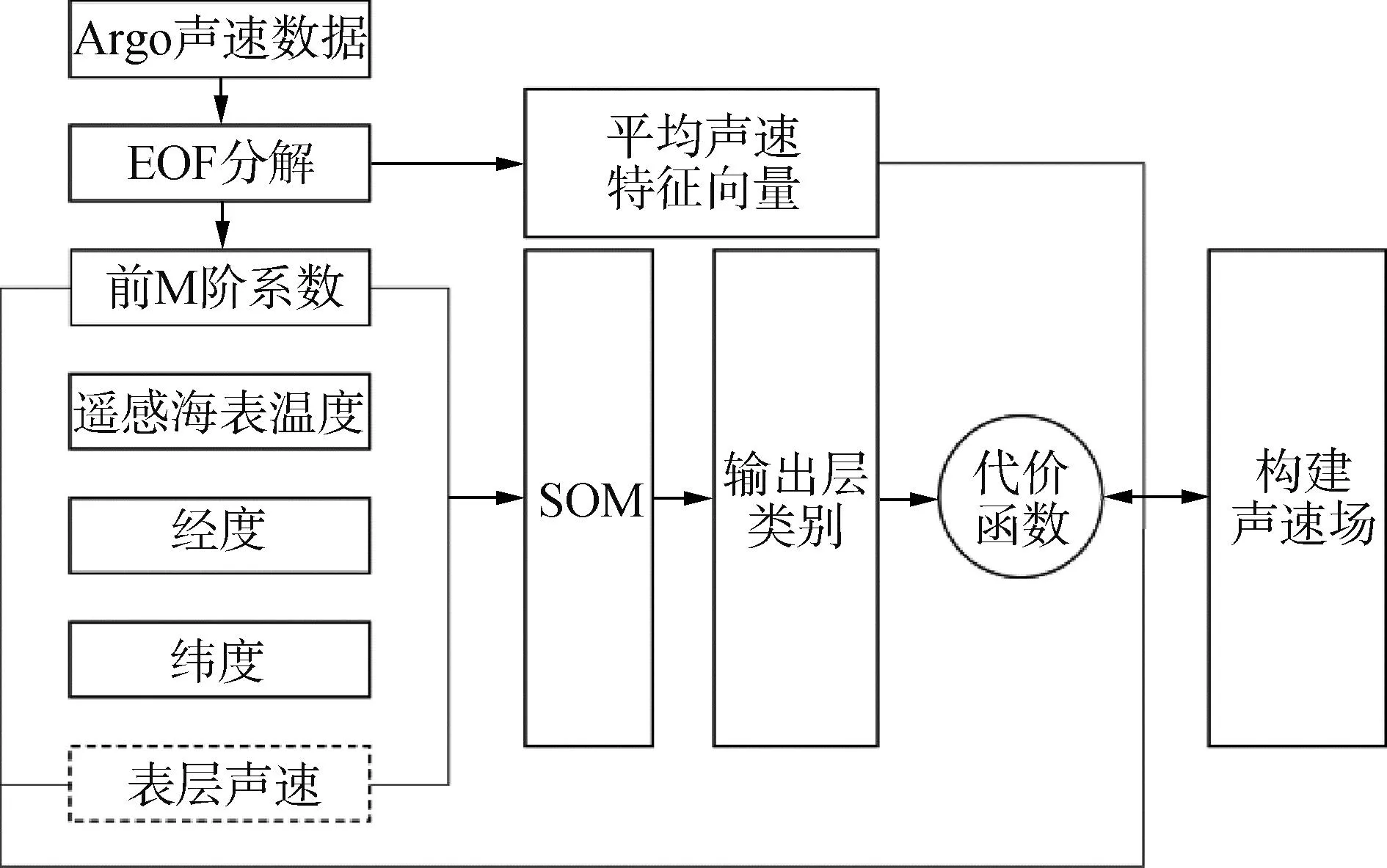
图10 SOM声速场构建模型Fig.10 SOM-based model for SSP construction

2.4 典型声场测量模式

在匹配场处理、压缩感知与深度学习声速场构建框架中,利用声场观测数据来进行声速场反演的模式在精度上现阶段仍高于无声呐观测数据的情况。在声场信息测量方面,美国斯克里普斯海洋研究所早期采用单输入单输出(single-input single-output,SISO)系统进行声场测量,利用多径信号反演环境声速分布[36]。为了增加声场数据测量的信息量,减小环境噪声对于测量精确度的影响,美国海军实验室在验证匹配场处理声速反演算法时,采用单输入多输出(single-input multiple-output,SIMO)系统[37],以船舶拖曳垂直阵列的形式实现,如图11(a)所示。

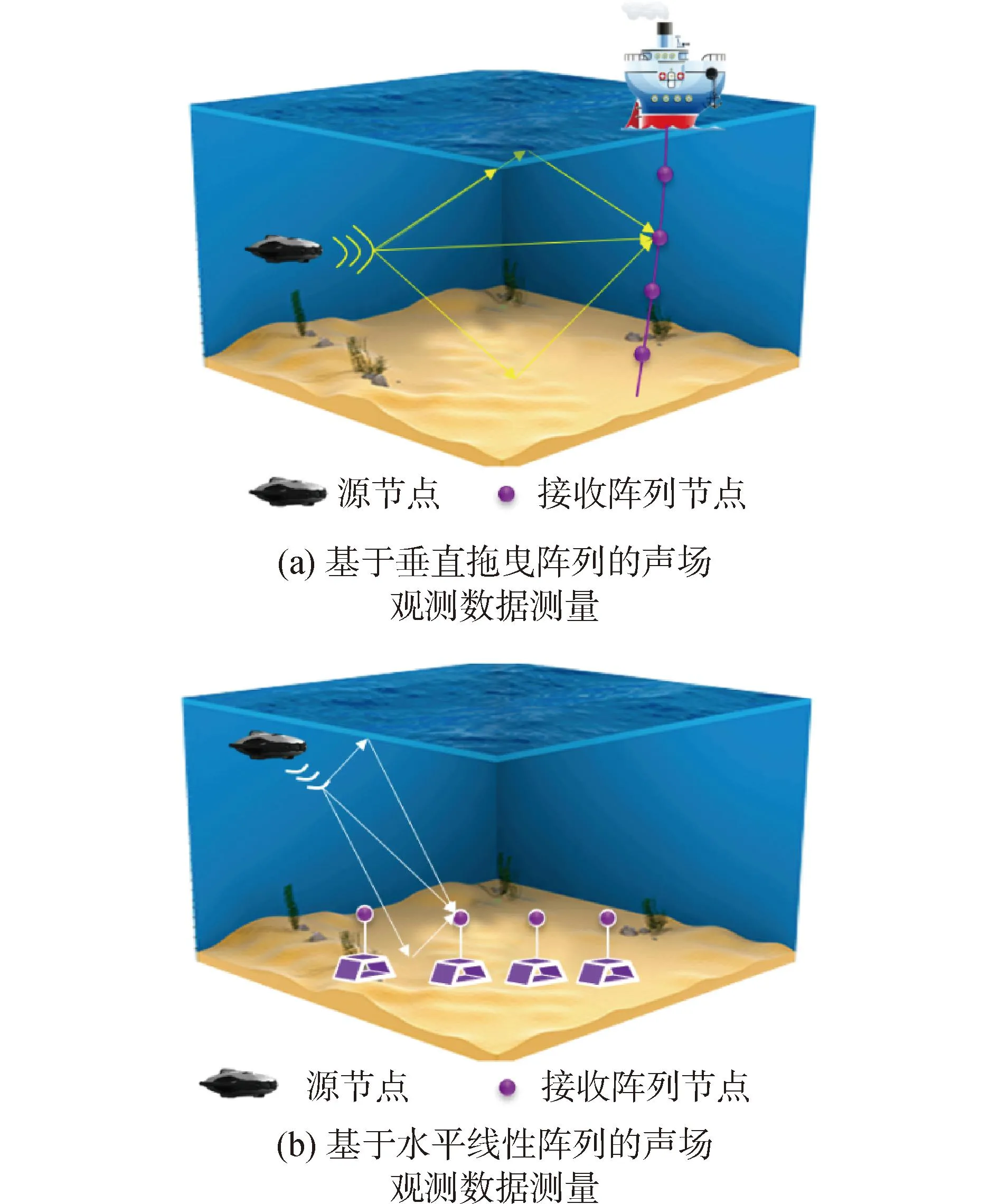
图11 声场观测数据测量方法Fig.11 Measurement method of sound field observation data

中科院声学研究所针对垂直阵列姿态不稳定的缺陷,提出采用海底水平阵列进行匹配场处理实现声速剖面反演的方法,并成功获取浅海声速反演结果[58-59],如图11(b)所示,但是由于海底阵列不利于回收再利用,因此设备生产经济成本高昂。

3 水下声速场构建方法比较

表2总结了不同声速场构建方法的基本属性。其中构建精度按照从优到差分为高、较高、中、低等级。时间开销分为准备阶段和构建阶段,准备阶段可以离线完成,因此构建阶段的时间开销性能更为关键,按照从优到差分为短、较短、中、较长、长共5个等级,实际上,由于CTD、SVP、XCTD等设备属于直接测量法,其时间开销以小时、分为计算单位,而匹配场处理、压缩感知和深度学习模型属于声速反演方法,其时间开销通常以分、秒为单位计算,因此“长、较长”等级时间开销远大于“中、较短、短”等级。

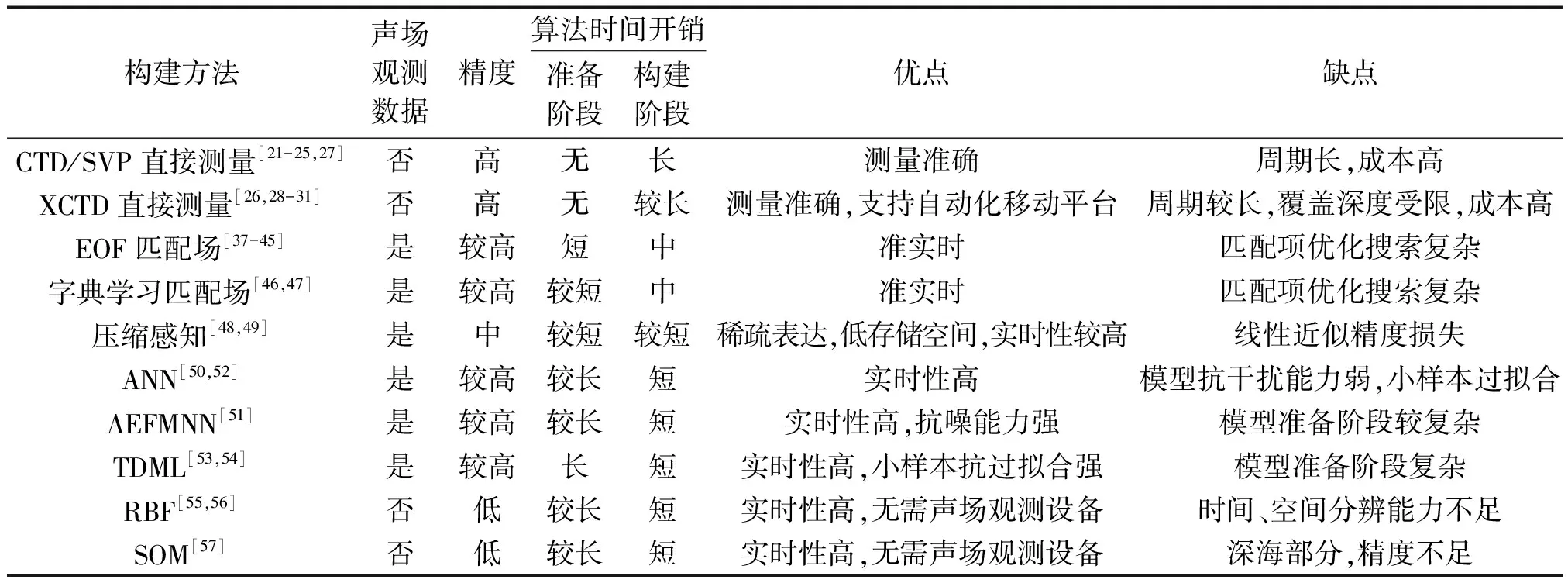
表2 声速场构建方法对比Table 2 Comparison of SSP construction methods

通过比较可以看出,直接测量法的最大优势在于其测量结果准确,通常可认定测量结果为真值,主要缺点则在于测量周期长,难以满足水下应用对于声速分布估计的实时性需求。在声速反演方法中,利用声场观测数据进行声速场构建的方法,其精度高于无声场观测数据的情况。压缩感知相比于匹配场处理,提高了实时性,但是牺牲了精度;神经网络模型相比于上述2种方法,精度和实时性均表现更好,但实质上其实时性优势是以牺牲准备阶段的时间开销为代价。对于RBF和SOM模型,其最大优势在于不受声场观测数据的约束,因此能够广泛适用于全球各个地区,且极大降低了水下声学设备成本,但是RBF模型经过指定时空区域数据训练后,其时间、空间分辨的泛化能力不足,而SOM模型对于季节跃变层、深海等温层的拟合精度不足。

随着传感技术、机器人技术的发展以及历史观测数据的长期积累,声速场构建方法整体趋势向着智能、实时、精确的方向发展。一方面,数据源的增多,意味着声速场构建的方法选择性提高,在不同地区,根据可获取数据源的不同,弹性化进行声速场构建将是满足未来水下用户对于声速分布估计的准确度或实时性需求的一种优秀的解决方案;另一方面,在无声场观测数据情况下,如何利用历史观测数据与能够通过遥感或海面快速测量的先验信息智能化地、高精度地构建全海深声速场,仍然是一个值得深入探索的研究点。

4 结束语

本文介绍并调查了当前水下声速场构建的研究现状,从构建方法上将其分为直接测量法和声速反演方法两大类。对于直接测量法,本文调查并列举了目前成熟商用设备仪器,列举了其主要性能参数;对于声速反演方法,本文根据其构建声速场的原理,总结了匹配场处理、压缩感知和深度学习三大框架,通过对各框架具体方法的原理分析,对比了不同声速场构建方法的优缺点,并归纳出声速场构建方法的演化趋势,即向着智能、实时、精确的方向发展。现有的声速场实时构建方法对于声场观测数据的需求与昂贵的水下声场测量设备生产成本不匹配,限制了水下声速反演方法的普适性,因此,如何在无声场观测数据情况下,能够利用有限先验信息进行智能化、高精度地全海深声速场构建,是未来研究的一大趋势,而如何利用多源观测数据,弹性化为水下用户提供不同精度、实时性需求的声速分布估计服务,是未来研究的又一大趋势。本文的工作将为后续水下声速场构建的研究工作提供参考。