燃料电池接触电阻与温度相关性研究
杨 铠,王 涛,沈喜训,孙 毅
(1.上海电力大学 环境与化学工程学院,上海 201306;2.上海空间电源研究所,上海 200245)
0 引言
不同类型的燃料电池中,低温质子交换膜燃料电池的正常工作温度在60~95 ℃[1-2]。基于磷酸掺杂聚苯并咪唑(PBI)膜的高温聚合物电解质膜燃料电池(HT-PEMFC)[3]工作温度为120~180 ℃。高温质子交换膜燃料电池具有更简化的水热管理,但与此同时,工作温度的升高也将对双极板(BPP)等部件的选材要求更加苛刻[4-5]。因为高温将导致双极板材料的更加容易被腐蚀或者氧化钝化[6],降低极板导电性,影响其在实际环境中的运行。所以,双极板的研发必须以具有良好的耐腐蚀性和导电性目标。否则,金属双极板腐蚀或者表面钝化产生钝化膜降低双极板电导率,导致双极板与气体扩散层(GDL)之间的接触电阻增大,增加整个PEMFC系统的功率损耗[7]。研究接触电阻对温度的敏感性也就显得至关重要。
温度对接触电阻的影响主要源自温度对相互接触的两个材料性能的影响[8],包括电性能和力学性能,比如电阻率、杨氏模量、热膨胀系数等。因此,温度对接触电阻的影响受多个因素耦合控制[9-10]。关于燃料电池中温度对接触电阻的研究还比较少,不过已经有大量学者对接触电阻的其他影响因素进行研究。其中部分学者对SOFC[11-12]和PEMFC[13-16]中存在的接触行为进行建模。使用不同的模型和实验方法在不同的尺度上对接触现象进行了研究。ZHOU 等[17-18]开发了一个基于表面轮廓的微尺度统计模型,用于模拟质子交换膜燃料电池中BPP-GDL 界面之间的接触行为。WU 等[14]利用分析模型对前者的工作进行了进一步总结。此外,还对载荷存在下的碳纤维弯曲现象及其对接触电阻的影响进行了量化。MISHRA 等[16]提出了一个基于材料表面粗糙度的分形模型,用于预测接触电阻,该模型将接触电阻表示为接触压力、材料特性和界面表面几何形状的函数。通过引入一个结构参数来量化粗糙表面,建立了一种与尺度无关的方法。LEE 等[19]使用有限元分析(FEA)程序来模拟使用金属BPP 的PEMFC 单电池的组装。同样,ANDRE 等[20]探索了金属BPP 表面形貌对接触电阻的影响。WANG 等[21]在MEA 和GDL 之间放入压敏膜,以测量使用传统端板组装的PEMFC 中的压力分布,并与使用新设计的液压端板获得的压力分布进行了比较[22]。AVASARALA 等[23]使用具有不同表面粗糙度的样品进行实验,研究了BPP 表面粗糙度对接触行为的影响。结果表明,仅仅通过降低材料接触表面的粗糙度不一定能降低接触电阻。金属双极板表面粗糙度对接触电阻率影响较大,而且与碳纸种类相关,电堆生产时需要考虑碳纸与双极板的匹配问题,在确定碳纸种类后选择具有合适表面形貌的箔材。DEBANAND 等[24]通过建 模和实验研究了工作温度对石墨双极板与碳纸间接触电阻影响。
本文研究内容是建立双极板和气体扩散层之间接触电阻的数学模型,在模型中引入温度参数,以研究温度对接触电阻影响规律,为将来燃料电池部件的选材和性能优化提供参考。
1 界面接触电阻
1.1 接触电阻原理
实际上,材料表面是粗糙的,如图1 所示,当粗糙表面相互靠近时,最高的粗糙峰点最先接触。通常会出现高的局部应力,使接触点产生很强的压缩作用,并使新的粗糙峰顶参与接触,承受绝大部分载荷[6]。当接触的粗糙峰顶数目增加到足以承受所施加的载荷时,以上的接触过程趋于完成。这种方式的接触,被定义为“实际接触”。实际接触的面积远小于名义接触面积(大约小两个数量级)。电流通过这些接触斑点从一个导体流向另一个导体时,由于电流收缩效应引起的收缩电阻称之为接触电阻[16]。

图1 两个粗糙表面接触过程Fig.1 Contact process between two rough surfaces
双极板与扩散层接触如图2 所示,双极板(Bipolar Plate,BPP)和扩散层(Gas Diffusion Layer,GDL)组件的总电阻除了各自的本体电阻外,还包括两者由于接触而产生的界面接触电阻。由BPP和GDL(Gas Diffusion Layer,GDL)组合产生的总电阻表示为
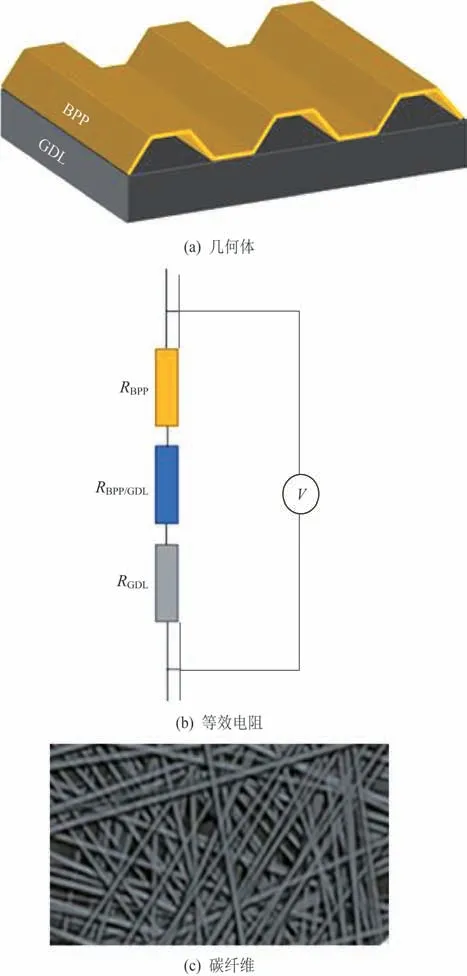
图2 双极板与扩散层接触Fig.2 Schematic diagram of contact between the bipolar plate and the gas diffusion layer
式中:Rtotal为总电阻;RBPP/GDL为极板与扩散层的接触电阻;RBPP为极板体电阻;RGDL为扩散层体电阻。
1.2 接触电阻建模
微观层面上,接触电阻主要受界面接触表面形貌的影响。假设:
1)双极板表面在微观尺度上具有类球形凸起,其半径rb,μm;
2)当前气体扩散层多采用碳纸,由若干碳纤维层层堆叠而成,且每一层碳纤维随机定向,碳纤维平均直径,即ra≈3.5 μm;
3)由于双极板的峰顶高度的标准差小于气体扩散层中的碳纤维的平均直径;
4)接触现象仅发生在第1 层碳纤维与金属双极板表面微凸体之间。
此外,除了界面处的微观表面形貌外,材料的杨氏模量、硬度、电导率等性能也会影响界面处的接触电阻。
为便于对接触电阻进行建模,进一步假设:
1)外力引起的形变为弹性形变;
2)粗糙度高度服从正态分布;
3)接触点一一分离,且任两个接触点变形互不影响;
4)碳纸由多层碳纤维构成,相邻两层碳纤维没有交插;
5)忽略单根碳纤维的弯曲。
接触现象的产生与分析可以追溯到外力作用下界面处出现的微凸体的变形,如图3 所示。

图3 粗糙体接触Fig.3 Schematic diagram of asperity contact
外加载荷引起的微凸体变形是指由于接触对各自的平均粗糙高度之间的间距变化而引起的微凸体高度变化。在无载荷情况下,“界面厚度”相当于两个接触面的平均粗糙高度之和。随着载荷的增加,粗糙体发生变形,导致接触面积的增加,从而引起接触电阻降低。外加载荷Fc作用下微凸体高度的变形δ由赫兹公式给出:
式中:Eq为接触表面的等效杨氏模量;Eq(T)为与材料、温度相关的杨氏模量。
Eq(T)值由式(3)计算,其中求和的两项分别为两者各自的材料参数:
式中:v1、v2分别为相互接触的两种材料的泊松比;E1、E2分别为相互接触的两种材料的杨氏模量;β(T)为温度相关的参数,其表达式为[25]
式中:T为温度,K。
当半球形微凸体与无限平面逐渐发生相互作用时,接触斑点近似呈圆形,且圆形接触斑点半径随外加载荷的增大而增大。平面与粗糙峰相互作用的接触半径(rc)是粗糙面与变形δ的粗糙峰顶点半径ra的函数,如式(5)所示:
单个接触对形成的面的电阻可由Holm[26]经典理论估计:
式中:ρ1、ρ2为接触材料的过平面电阻率,可采用Bruggeman 法测量计算;材料电阻率与温度相关关系通过实验确定ρ。
当气体扩散层与金属双极板相互作用时,可以假设接触行为发生在半球与圆柱体之间,如图3 所示。在该条件下,接触面的等效接触半径估算如下:
为了将上述处理从单个接触点扩展到整个表面,假设微凸体高度的正态分布:
式中:σsum为峰顶高度的标准差。
总压力P可根据单个微凸体接触的压力Fc、峰顶密度Dsum、峰顶高度标准差σsum的平方根、气体扩散层中碳纤维可参与接触的面积分数以及微凸体高度大于平面间距的概率计算。
为了分析气体扩散层的孔隙率的影响,引入气体扩散层可参与接触的面积分数∑ε(xm,θm)。一个典型的气体扩散层表面具有不同长度(xm)和角方向(θm)的碳纤维。由于气体扩散层表面存在孔隙,即使双极板表面的微凸体高度超过面间距,也不是所有的微凸体都能接触到碳纤维。
式(9)和式(10)中的函数积分使用抛物柱形函数计算。式(9)和式(10)中带宽参数α通过式(11)计算[27]:
式中:m0、m2、m4分别为零阶矩、二阶矩、四阶矩。
峰顶密度Dsum通过式(12)计算[27]:
将四阶矩和带宽参数分别代入式(13)和式(14)可得峰顶半径rm和峰顶总和标准差σsum[27]:
2 接触电阻预测
2.1 粗糙表面参数
利用上一节中描述的接触电阻模型预测双极板和气体扩散层的接触电阻,需要通过测试确定表面的形貌特征数据。本文根据原子力显微镜(Atomic Force Microscope,AFM)获得双极板表面形貌(如图4 所示)的二维(2D)轮廓数据,采用文献方法[27]计算粗糙表面数值作为模型的输入参数,见表1。
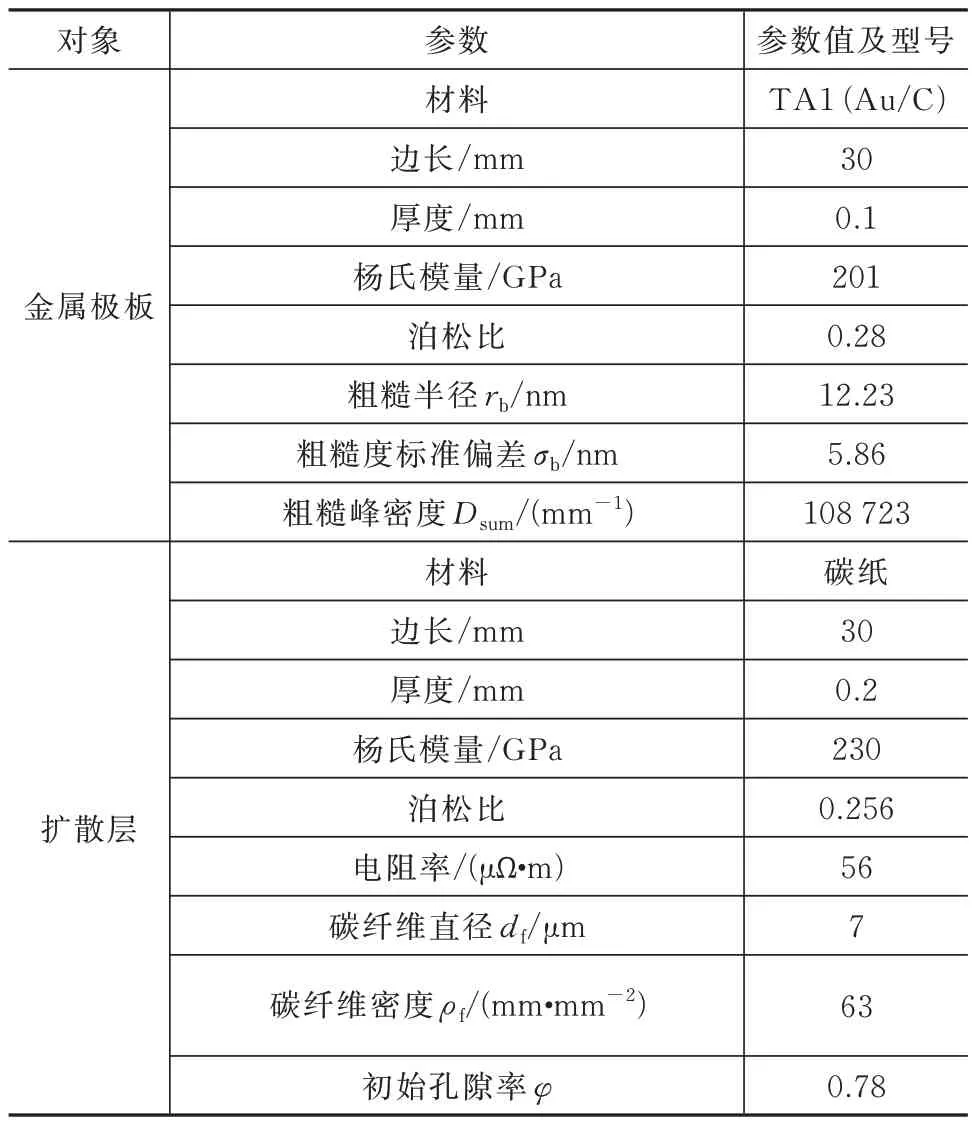
表1 双极板和气体扩散层材料物性及粗糙表面参数Tab.1 Physical properties and rough surface parameters of the bipolar plate and gas diffusion layer materials

图4 TA1 表面2D 轮廓Fig.4 2D Profile of the TA1 Surface
利用扫描电子显微镜(Scanning Electron Microscope,SEM)获取所需气体扩散层表面参数,得到了其平面表面显微图。如图5 所示,碳纸中圆柱形碳纤维的平均直径约为7.6 μm。通过图像处理技术(ImageJ)对碳纸的SEM 图像进行进一步分析得到碳纸可接触面积分数∑ε(xm,θm)约为0.3。本模型中引入了双极板和气体扩散层的相关表面参数,用于预测在60~180 ℃ 温度范围内双极板和气体扩散层界面在不同载荷下的接触电阻。另外,本模型所使用的材料在室温下的性能见表1。

图5 碳纸SEM 图Fig.5 SEM image of the carbon paper
2.2 体电阻率与温度相关性
钛(宝钛,TA1,100 μm)的体电阻率随温度变化的实验数据可在标准参考文献[28]中获得。常温下,TA1 的体电阻率在0.55~0.58 μΩ·m,碳纸的电阻率在56~58 μΩ·m,在200 ℃以内,随着温度升高,TA1 的体电阻率单调增加,而碳纸电阻率单调下降。TA1 和碳纸(东丽TGP-060,190 μm)电阻率随温度变化趋势如图6 所示,对于TA1,其电阻率ρ1(T)随温度T的变化可表示为

图6 材料过面电阻率随温度变化特性Fig.6 Variation of the material surface resistivity with temperature
对于碳纸,其电阻率ρ2(T)随温度T的变化可表示为:
2.3 模型预测结果
将参数代入模型,利用模型分别得到在60、100、140 和180 ℃ 时接触电阻与载荷之间的关系如图7 所示。在任一温度下,随着载荷的增加,接触电阻明显降低。在相同的外加载荷下,随着温度的升高,接触电阻值明显降低。例如,在初始0.2 MPa 和60 ℃ 时,双极板与气体扩散层之间的接触电阻值高达271 mΩ·cm2,当温度达180 ℃时,接触电阻降低至158 mΩ·cm2,降低幅度约为42%。随着压力的增加,温度变化的影响更加明显。当压缩压力保持在1.4 MPa,温度为60 ℃时,接触电阻达到192 mΩ·cm2。当温度升高到180 ℃时,该值降低至79 mΩ·cm2,降低幅度约58%。这是因为接触电阻受气体扩散层碳纤维电阻率随温度变化主导,气体扩散层中碳纤维的电阻率随温度升高下降的幅度影响超过金属电阻率升高的影响。温度的变化会导致材料本体电阻和接触电阻值的显著变化。
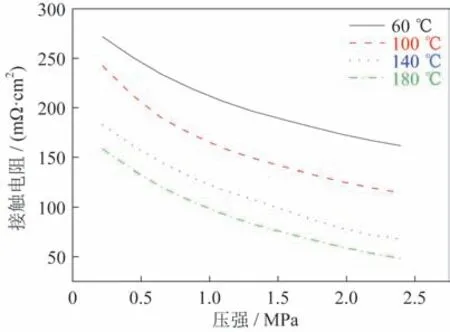
图7 接触电阻变化模型预测值Fig.7 Predicted values obtained by the contact resistance variation model
3 实验验证
3.1 实验步骤
本实验采用两步法验证接触模型的接触电阻。实验装置和实物如图8 所示。选用钛合金(TA1)及其分别具有金和碳涂层的平板材料作为实验样品,厚度为0.1±0.05 mm,形状为边长为30 mm 的正方形。对每个样品进行酸洗,以消除表面氧化层对接触电阻测量的影响。步骤1 如图8(a)所示,使用两张TGP-H-090 碳纤维纸(Toray Industries,Inc.)夹住极板样片,然后将其置于两块镀金铜板之间压紧。测试设备如图8(右)所示,通过气缸对试样在0.2~2.6 MPa 范围内的施加一系列压力,同时使用分辨率为0.1 μΩ 的数字微欧表(AT527A,Amber Corporation,China)测量整体电阻。步骤2 如图8(b)所示,电阻测量方法与步骤1 相同,区别为仅在两块镀金铜板之间夹一张碳纸。

图8 实验步骤和实物图Fig.8 Test procedure diagrams and physical image of the test device
Rexp1是碳纸与铜板的接触电阻、碳纸与极板样片的接触电阻和各部件体电阻之和。Rexp2是碳纸与铜板的接触电阻与碳纸自身的体电阻之和。因此,以TA1 极板为例,极板与碳纸的单位面积接触电RBPP/GDL可表示为
式中:RTA1、Rcp分别为TA1 和碳纸的本体电阻;ATA1/cp为钛板和碳纸的表观接触面积。
为了获得可靠的结果,相同条件下进行了3 次的重复测量。每次测量都使用一张同一批次新的碳纸,以减少上一次测量时因碳纸受压而造成的测量误差。
3.2 实验结果
TA1 和碳纸之间在不同温度和压力下的接触电阻实验结果如图9 所示。其中分别为在60、100、140、180 ℃的温度下,接触电阻随压力的变化。明显看出在任一温度下,接触电阻随压力增加而下降,且下降速度在1.2~1.4 MPa 时逐渐减缓。1.4 MPa压力下,3 种BPP 与碳纸的接触电阻随温度的变化如图10 所示,可以看出,随温度升高,3 种材料与碳纸的接触电阻均表现出下降的趋势,并且下降的幅度明显。钛基材、钛镀碳、钛镀金下降幅度分别为59%、37%、42%。此外,钛基材表面处理后,与GDL 之前的接触电阻下降明显,这是因为钛基材长时间暴露在环境中会形成氧化膜,导致基材的电阻率明显上升,也将导致接触电阻的增加,因此,极板使用合适的表面处理工艺加工以保证其具有良好的耐蚀性与导电性十分必要。
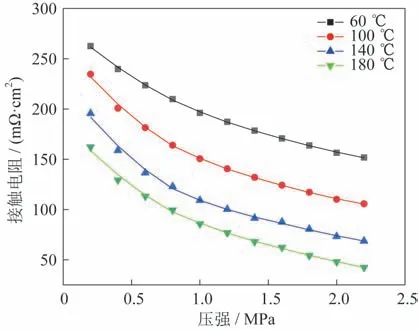
图9 不同温度下钛与碳纸的接触电阻随压力变化Fig.9 Variations of the contact resistance between the titanium sheet and carbon paper under different temperatures and pressures

图10 不同涂层极板与碳纸的接触电阻随温度变化Fig.10 Variation of the contact resistance between different coated plates and carbon paper under different temperatures
模型与实验结果的对比如图11 所示,模型结果要稍微大于实验结果,可能是因为模型忽略了GDL塑性形变及热膨胀等因素的影响,但总体误差在10%以内,属于合理误差范围。因此,该模型可在已知双极板与气体扩散层表面参数、材料特性的情况下,对两者接触电阻进行预测。
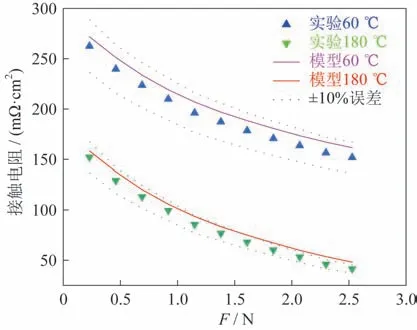
图11 60℃和180℃模型与实验结果对比Fig.11 Comparison between the models and test results at 60 ℃ and 180 ℃
除了对双极板和气体扩散层之间的接触电阻进行测试之外,还测试了同种材料的BPP 之间的接触电阻。结果如图12 所示,3 种金属材料的BPP 各自的接触电阻随温度升高均升高,因为3 种材料的电阻率随温度升高均升高,且强度在200 ℃范围内变化很小。该结果也从侧面佐证了气体扩散层电阻率随温度变化特性对双极板和气体扩散层之间的接触电阻随温度变化的重要作用。
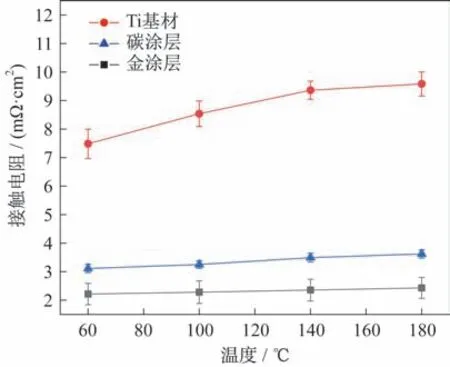
图12 涂层对双极板接触电阻的影响Fig.12 Effect of coating on the contact resistance of bipolar plates
3.3 影响因素研究
接触表面的参数,如等效微凸体半径、峰高标准偏差、BPP 粗糙峰密度和GDL 的接触面积分数,对接触行为起着重要作用。因此,对参数敏感性的研究具有重要意义。
这些参数每一个都是独立变化的,可对其逐一进行研究,除目标参数外,保持其他参数不变,将其对接触电阻的影响作为施加压力的函数反映在图中。图13(a)探讨了在180 ℃时等效微凸体半径的变化对接触电阻的影响。如图13(a)所示,微凸体等效半径的减小导致接触电阻的减小。这是因为微凸体等效半径的减小会导致接触斑点更小,但是,接触斑点变小的现象会使得更多的微凸体参与接触行为。单个接触点面积的减少和接触点数量的增加对接触电阻的影响相互制约,因此,仅通过调节双极板表面这一参数难以控制接触电阻,难以获得具有这一特定粗糙度的表面。微凸体高度标准偏差对接触电阻影响如图13(b)所示,当标准偏差值增大时,接触电阻值增大。峰顶高度的标准差表示表面的粗糙度。当它增加时,在任何给定的表面分离处接触的微凸体就会减少。如果参与接触的微凸体较少,接触的面积会减少,因此接触电阻也会升高。图13(c)反映了粗糙峰密度变化对接触电阻的影响,它在控制接触电阻值方面起着次要的作用。但是,这个参数必须根据气体扩散层的表面形态来选择,需要考虑二者之间的匹配,这是因为单纯增加顶密度并不能总是降低接触电阻,因为GDL 表面上的碳纤维数量可能会限制接触点的总数。图13(d)显示了接触面积分数变化(0.6~0.4)对接触电阻变化的影响。这是关键参数之一,高的接触面积分数,会增加微凸体接触几率,增大接触面积,从而得到较低的接触电阻。
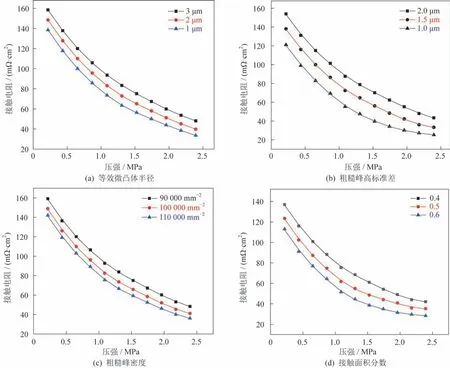
图13 粗糙参数对接触电阻的影响Fig.13 Effects of the roughness parameters on the contact resistance
4 结束语
本文针对数值模拟、实验验证、模型分析应用3部分内容进行了研究,分析了温度对金属双极板和气体扩散层之间接触电阻的影响规律。具体如下:
1)基于碳纸的多孔结构和金属双极板的表面微观粗糙形貌,将碳纤维等效为圆柱体,将金属双极板表面微凸体等效为球体,建立单个触点的几何模型,分析接触形变的过程,计算单个触点平均等效接触半径与压力之间的关系,然后将温度对材料电阻率以及杨氏模量的影响引入单个触点接触电阻的计算式中,计算等效接触半径和接触电阻之间的关系,最终即可得到一系列载荷作用下,温度对接触电阻影响规律。
2)分别进行了钛、钛镀金、钛镀碳双极板和碳纸之间的接触电阻实验测量,结果表明,在某一恒定的压力下,3 种极板和碳纸之间的接触电阻均随着温度的上升而下降。主要原因是碳纸的电阻率随温度的上升而下降,且其降幅对接触电阻下降的促进作用强于金属双极板电阻率随温度上升而上升对接触电阻下降的抑制作用,同种金属之间接触电阻随温度上升而上升也从侧面证实了这一点;此外,温度上升材料的等效杨氏模量也下降,相互接触时,材料更容易发生形变而增大接触面积,导致接触电阻下降。
3)将材料与温度相关的杨氏模量、电阻率及测试并进一步计算所得的粗糙表面数据参数值代入模型,对接触电阻进行预测,然后将预测结果和实验结果进行对比,60 ℃和180 ℃时,两个结果误差均在10%之内,证明模型具有可靠性。利用模型分析粗糙度参数对接触电阻的影响规律,发现微凸体等效半径和粗糙峰密度之间相互关联,综合影响接触电阻的变化,难以单独讨论。而微凸体峰高标准差减小会导致接触电阻减小,相反接触面积分数减小会导致接触电阻的增大。
本文建立了温度对接触电阻影响的数学模型,对于将来分析某些高温应用场景下(比如高温质子交换膜燃料电池)接触电阻的变化规律提供了参考。

