复杂形态碎石颗粒的三维离散元模拟及试验验证

程晓颖, 乔婷, 秦建敏, 季顺迎

(1. 大连理工大学 工业装备结构分析优化与CAE软件全国重点实验室, 辽宁 大连 116024;2. 大连大学 建筑工程学院, 辽宁 大连 116622)

0 引 言

碎石颗粒多由山石风化破碎而成,因其具有较好的强度和硬度,被广泛应用在交通土建工程中,如坝体工程和碎石桩的填料,修筑碎石路基结构等。碎石颗粒有尖锐棱角,形状、纹理呈不规则状态,具有典型的离散性、非连续分布特征,在数值方法上大多采用离散元法进行研究。

离散元法是20世纪70年代CUNDALL等[1]为解决岩石力学问题而提出的。目前,采用离散元法对具有明显离散特性碎石颗粒的研究已取得较多成果,在模拟碎石的非规则形状时大部分学者采用基于球单元的黏结和镶嵌模型。徐旸等[2]通过三维扫描技术构造具有碎石颗粒形态的球黏结模型,分析颗粒形状对碎石力学性能的影响。ZHAO等[3]采用球镶嵌模型建立碎石离散元数值模型,并进行休止角和直接剪切试验的数值研究,但基于球体填充方式构造的颗粒簇模型只能近似模拟碎石颗粒的基本几何特征,虽然模拟精度会随着球单元数量的增加而提高,但也会使模型计算效率急剧下降,且颗粒簇模型较难模拟碎石颗粒的尖锐棱角特征。

碎石的棱角特征对其力学性能有重要影响,非常有必要构造更适合描述碎石颗粒非规则形态的离散单元[4-5]。QIAN等[6]采用三维多面体块对碎石颗粒进行离散元模拟,预测土工格栅加固碎石试样的强度特性。BIAN等[7]采用多面体单元建立有砟轨道模型,探究动静载荷下单个颗粒的滚动和滑动。多面体单元可合理模拟碎石颗粒尖锐棱角,且能模拟颗粒间重要的互锁现象,但以上学者构造的离散多面体单元均为凸多面体,真实碎石颗粒除有凸出的棱角特征外还有一定的凹陷[8],凸多面体单元不能完全模拟,而用凹多面体单元同时模拟碎石颗粒棱角特征和凹陷特性的文献又较少。

由于散体碎石颗粒间没有黏结作用,碎石构筑物的稳定性主要依靠颗粒间的咬合互锁和摩擦作用。休止角试验常用于探究散体碎石颗粒间的摩擦作用,对碎石颗粒开展休止角试验,可探究不同粒径、形状和级配碎石颗粒对碎石边坡稳定性的影响[9-10]。此外,休止角还与许多重要的现象有关,包括岩石和边坡坍塌、雪崩、岩石沉积行为等[11]。用离散元法建立颗粒材料休止角模型时,通过对比休止角试验与离散元模拟结果,可对碎石颗粒材料进行参数校准,得到离散元模拟时的近似计算参数[12]。可见,休止角试验在表达碎石颗粒材料的流动特性和评价碎石构筑物稳定性方面具有较好的优势。

在碎石构筑物中,碎石集料必须具有足够大的强度来承受外部载荷,而测定集料强度较简便、快速的试验方法就是直接剪切试验(以下简称为直剪试验)。考虑到碎石粒径较大,因此采用大型直剪试验仪研究非连续、非均质碎石颗粒的剪切性能。通过大型直剪试验,可探究含水率和碎石含量对土石混合体冻融交界面剪切强度的影响[13],并分析法向应力、剪切速率、碎石粒径等因素对剪切界面剪切力学特性的影响和接触面剪切破坏机理[14-15]。另外,在进行室内试验的同时,还可对碎石颗粒材料进行离散元直剪模拟,通过不同垂直压力下的直剪试验模拟,分析试样在剪切过程中的体积变化和力学行为[16],探究土石混合料骨架结构的力传递路径和混合料变形破坏机制[17-18]。可见,通过室内大型直剪试验和对应的离散元模拟,可探究碎石颗粒材料的剪切破坏和细观特性。

本文为模拟碎石颗粒的棱角特征和凹凸特性,并合理表达各项力学性能,利用三维激光扫描技术获取碎石颗粒的表面几何形貌,将基于能量守恒接触理论的多边形网格离散元法引入到碎石颗粒离散元模型的构造中,建立具有真实碎石颗粒尖锐棱角和凹凸特性的多面体单元,开展碎石颗粒的休止角和直剪试验的离散元模拟,结合室内试验,分析碎石颗粒的流动性和剪切特性。

1 碎石颗粒的离散元构造

碎石颗粒棱角分明且具有凹凸特性,是典型的非规则几何形貌。非规则颗粒系统在单元排布、运动形态及动力过程等方面与球形颗粒差异很大。为此,采用多面体离散元法构造多面体单元,模拟碎石颗粒的真实几何形貌,表达其凹凸特性。

1.1 碎石任意形态多面体模型的构造

为模拟碎石颗粒的尖锐棱角和凹凸特性,用三维激光扫描技术获取碎石颗粒的三维表面几何形态。图1为三维激光扫描系统,3D激光扫描仪基于激光测距原理记录碎石表面的三维坐标信息。碎石颗粒形态各异,形状不尽相同,为满足其多样性,本文扫描200多个不同形状、粒径的碎石颗粒以备使用。

图1 三维激光扫描系统

由真实的碎石颗粒扫描得到的表面三维坐标信息有几十万甚至几百万个(见图2),基于该坐标点云直接构造多面体单元并开展离散元模拟,会极大降低数值计算效率,因此有必要对扫描的点云数据进行简化处理。

图2 真实碎石颗粒及其对应的扫描点云信息

本文采用曲率删减的方法不断减少碎石模型的点云数据量,并对同一碎石模型不同点云数量下所构造颗粒的直径和球形度进行分析比较,发现点云数量在100个左右时所构造的碎石模型相对真实颗粒的直径和球形度误差较小。因此,使用由约100个点云和约200个三角面围成的多面体模拟碎石,在提高离散元数值计算效率的同时,还保留碎石的主要棱角特征和凹凸特性。

图3为同一碎石颗粒曲率删减后得到的不同点云数量的碎石表面点云信息。将最终简化得到的点云坐标和创建的三角面边界矩阵导入多面体离散元程序中,构造由三角面围成的封闭不规则多面体单元,见图4。

(a)46 657个

图4 多面体单元

1.2 多面体单元能量守恒接触模型

多面体离散单元间的接触模型符合能量守恒接触理论[19],即假设2个颗粒当前的接触状态,包括法向接触力Fn和接触力矩Mn,可以由接触能量函数进行描述。接触能量函数是关于2个颗粒当前位置和方向的函数,

(1)

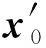
(2)

(3)

以法向接触方向n作为Fn的单位矢量,

(4)

接触点xc可由下式确定:

(xc-x)×Fn=Mn

(5)

(6)

式中:x为参考点坐标;λ为一个自由参数。

假设2个颗粒接触时发生体积重叠,1个合适的接触势能函数应考虑接触时重叠区域的基本特征。FENG[20-21]提出关于接触体积单调递增的势能函数:

ω=ω(Vc)

(7)

式中:Vc为接触区域ΩA的体积。

势能函数在法线方向的1阶偏导为法向接触力Fn,

Fn=-∇xω(Vc)=-ω′(Vc)Sn

(8)

式中:Sn为接触面积S1的矢量面积,

(9)

接触面积S1见图5中左侧区域。

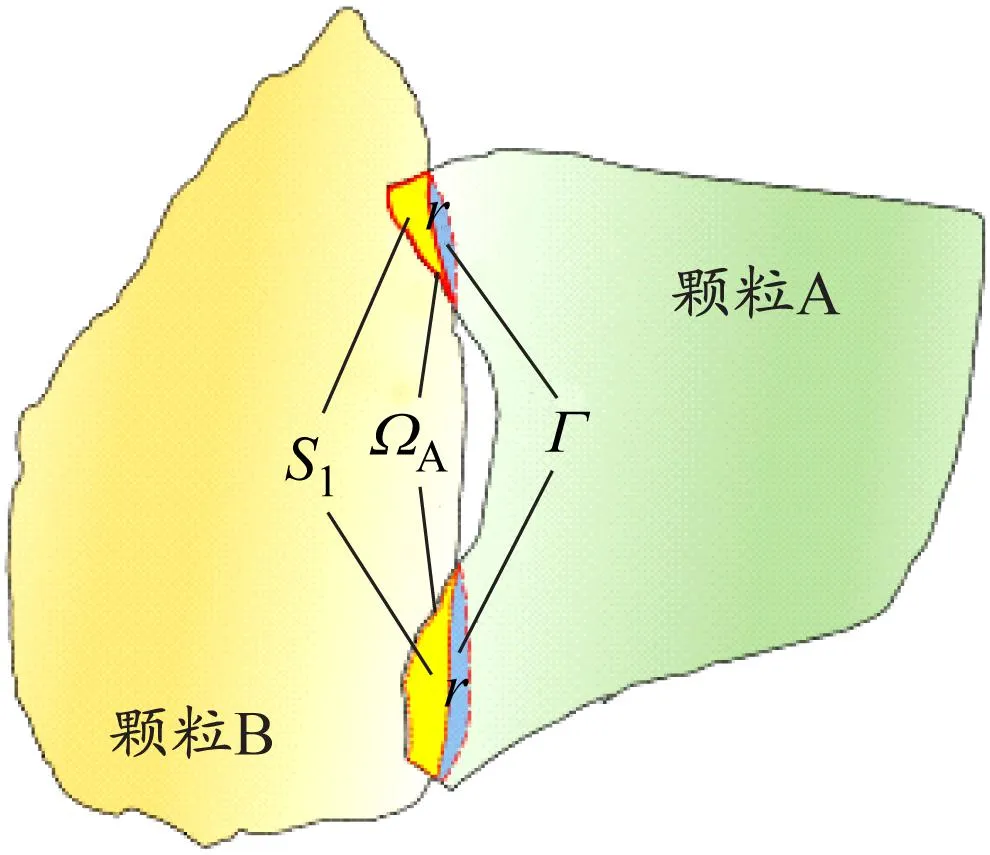
图 5 2个颗粒接触时重叠区域示意

单位法向接触向量n和接触点xc分别定义为:

(10)

(11)

(12)

式中:Gn为接触面S1的一个向量化“静态力矩”。

基于接触体积的线性接触能量函数为

ω(Vc)=knVc

(13)

其1阶导数

ω′(Vc)=kn

(14)

式中:惩罚因子kn表示法向接触刚度。

Sn由FENG[21]的一个算例计算得到:

(15)

多边形网格离散元程序中的临界时间步长由下式计算得到:

(16)

(17)

式中:R为最小颗粒的半径;G为剪切模量;ρ为颗粒密度;E为弹性模量;υ为泊松比。

2 碎石颗粒休止角的离散元分析及验证

休止角作为碎石颗粒重要的物理力学特征参数之一,不仅能反映碎石的流动特性,而且是评价碎石构筑物稳定性的重要指标。为探究碎石颗粒材料的流动特性,并验证结合三维扫描技术所构造的多面体单元模拟碎石颗粒的合理性,建立多面体单元的休止角离散元模型,并进行对应的室内试验。

2.1 构建休止角离散元模型

碎石等颗粒材料受重力等作用形成的稳定而不坍塌的堆积体,其最大坡角称为碎石休止角。目前,针对特定散体颗粒材料测量休止角的方法主要有固定漏斗法、旋转圆筒法、无底圆筒法等。对于粒径较大的碎石,大多采用无底圆筒法[22-23]测量其休止角。

本文采用无底圆筒法建立碎石颗粒的休止角离散元模型,其中碎石颗粒为结合三维扫描系统构造的多面体单元,其级配曲线见图6,对应的碎石颗粒见图7,图中的数值为对应碎石颗粒直径。

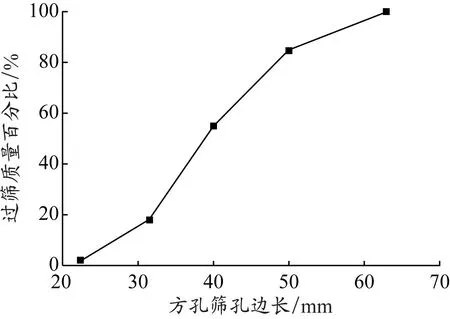
图6 多面体单元级配曲线

图7 级配碎石颗粒试样,mm

休止角数值模型见图8(a)。给定2个边界,一个为水平底面,尺寸为长×宽=2 m×2 m,另一个是直径250 mm、高1 000 mm的无底圆筒。多面体碎石单元在圆筒内自然堆积,堆积高度为750 mm,此时圆筒内有600个多面体单元。数值试验开始时,给无底圆筒施加恒定的速度,使其沿竖直方向缓慢向上移动,见图8(b)。试验过程中,多面体碎石单元从圆筒底部落下并最终形成稳定的堆积体,见图8(c)。

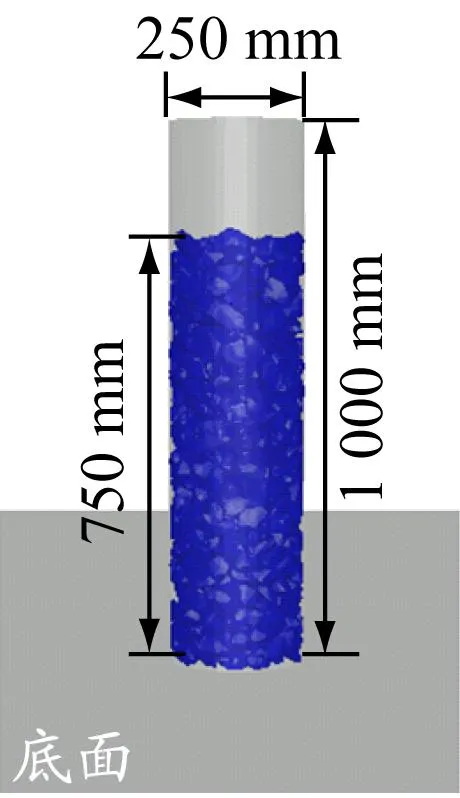
(a)t=0

颗粒材料休止角的测量方法一般是直接计算[24],即测量圆锥状堆积体的底面直径和高度,再用反正切函数计算其休止角。碎石颗粒粒径较大,不易像细沙等细小颗粒能堆成标准的圆锥状堆积体;同时,碎石堆积体的坡面并非直线,其轮廓不规则,没有明显的圆锥顶点,运用常规的直接计算方法不能准确获得碎石休止角,需要用更合适的方法测量碎石休止角。

根据碎石堆积体主视图(见图9(b)),提取碎石堆积体外轮廓线进行线性拟合,由直线斜率求得对应位置的休止角,即图9(a)中A、B、C、D等4点对应的休止角度分别为29.89°、33.32°、29.38°、29.00°,计算得到碎石最终的休止角为30.40°。堆积体轮廓线线性拟合的相关系数R2均大于0.9,证明拟合坡面轮廓线的方法合理,所测碎石休止角有效。碎石颗粒休止角模型的主要计算参数见表1。

(a)碎石堆积体俯视图

2.2 碎石颗粒室内休止角试验验证

为验证碎石颗粒休止角离散元模拟结果的准确性,开展对应的室内休止角试验。如图10所示为自制的测量碎石休止角的试验装置及其示意图,无底圆筒尺寸与离散元模型一致,将圆筒放置在水平底面上,装入同级配的碎石颗粒。由液压手动堆高车牵引圆筒使其缓慢、均匀地竖直向上移动,碎石颗粒在重力作用下落在水平底面上,最终形成稳定而不坍塌的碎石堆积体。

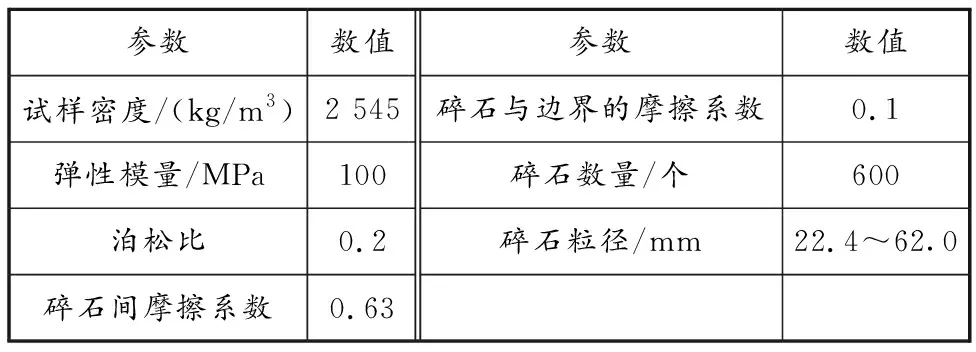
表 1 碎石颗粒休止角模型的主要计算参数

(a)试验装置

拍摄碎石堆积体试样的主视图(见图11(b)),提取图像中碎石堆积体的外轮廓线,对其进行线性拟合,以拟合的直线斜率计算对应位置的休止角θ。

单次试验的测量结果具有一定的随机性,误差较大,如手动堆高车的提升速度、碎石颗粒的排布、相机拍摄的角度等都会对休止角的结果产生误差。为提高碎石休止角试验结果的准确性,在相同试验条件下对同一级配碎石进行7次重复试验并获得对应休止角,取7次休止角试验结果的平均值作为最终的碎石休止角,见表2。

表 2 碎石颗粒休止角的试验结果

由表2可知,重复试验中同一位置的休止角有一定的波动变化,证明重复试验的必要性,本文7次重复试验结果的平均值31.76°作为碎石颗粒的休止角是可信的。

碎石颗粒休止角室内试验结果与离散元模拟结果对比见图12,其中离散元模拟的休止角结果为30.4°,与室内试验结果的相对误差为4.2%。误差的原因一方面是圆筒提升速度,在室内试验中使用液压手动堆高车手动操作控制,而离散元模拟是给圆筒施加恒定速度;另外,碎石颗粒在圆筒内的堆积排布也存在一定差异。尽管如此,二者的差异仍处于适度范围内,故由多面体单元建立的模型在适当置信度下可以预测碎石的休止角。

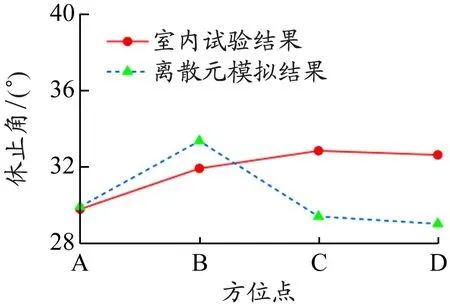
图12 碎石颗粒休止角室内试验与离散元模拟结果对比

通过休止角室内试验,验证本文所构造的多面体单元不仅可以合理地模拟碎石颗粒,准确表达其流动性,而且为采用多面体离散元法研究碎石等不规则颗粒材料的复杂力学性能提供一定的依据。

3 碎石颗粒直剪离散元模拟及试验验证

在岩土工程中,常用直剪试验测定土体的剪切强度。为进一步验证结合三维扫描技术所构造的多面体单元在探究碎石力学性能方面的可靠性,建立碎石直剪离散元模型。针对碎石颗粒尺寸大的特点,采用大型直剪仪对碎石颗粒进行直剪离散元模拟和对应的室内直剪试验验证,在验证多面体单元模拟碎石颗粒合理性的同时,探究碎石颗粒的剪切特性。

3.1 碎石颗粒直剪离散元模拟

大型直剪试验仪包含上、下剪切盒和上盖板,其中上、下剪切盒的尺寸分别为0.4 m×0.4 m×0.2 m和0.5 m×0.4 m×0.2 m,且在上剪切盒底部增加长、宽分别为0.4 m×0.1 m的挡板,防止剪切时下剪切盒中外露碎石颗粒被挤出,见图13(a)。剪切盒和上盖板均为三角面组成的刚性边界,碎石颗粒为多面体单元。

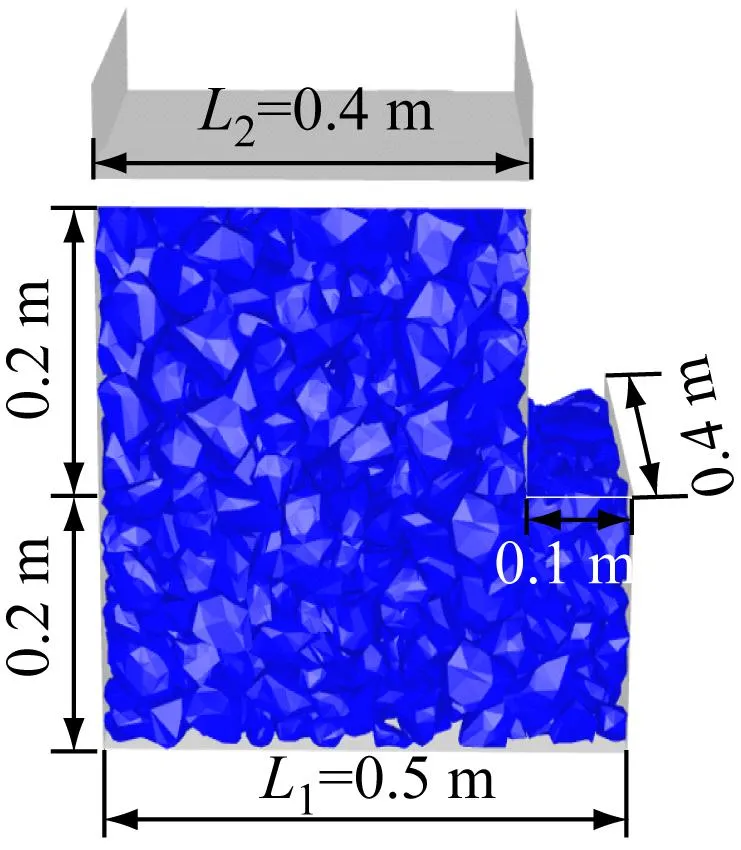
(a)离散元直剪模型

直剪离散元模型中碎石颗粒的级配与休止角试验一致,将多面体碎石单元混合均匀后分层放入剪切盒中,使用静压法在上盖板施加压力,对剪切盒内的碎石进行预压实。此时,剪切盒中孔隙率为0.384,有1 200个多面体碎石单元。

直剪试验开始,在上盖板上施加恒定法向载荷(20、50和100 kPa)的同时,在下剪切盒上施加恒定的速度,使其缓慢水平向左移动。剪切过程中上剪切盒始终保持固定不动,见图13(b)。当剪切位移达到75 mm即剪应变为15%时,结束试验。碎石颗粒直剪离散元模型的主要计算参数见表3。

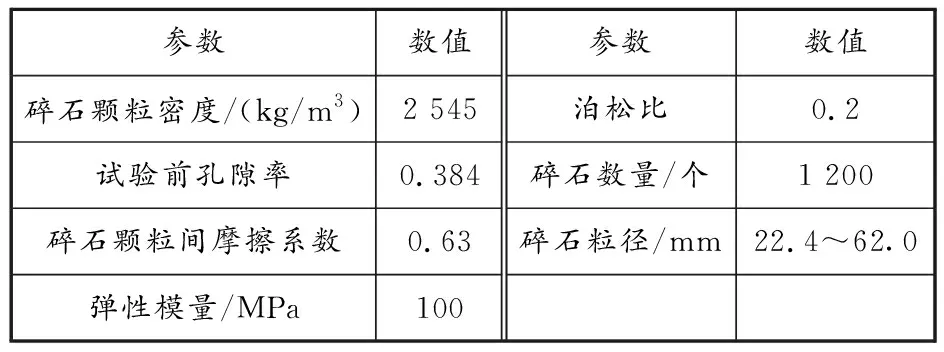
表 3 直剪离散元模型的主要计算参数

3.2 碎石颗粒室内直剪试验验证

为验证碎石直剪离散元模型的合理性,对碎石颗粒进行大型直剪试验。本文使用的大型直剪仪示意见图14,剪切盒的上下盒尺寸、碎石级配、施加的法向载荷均与离散元模型保持一致。将级配碎石混合均匀放入剪切盒内压实,通过控制法向制动器在上盖板上施加法向载荷,控制水平作动器使下剪切盒水平移动,完成直剪试验。

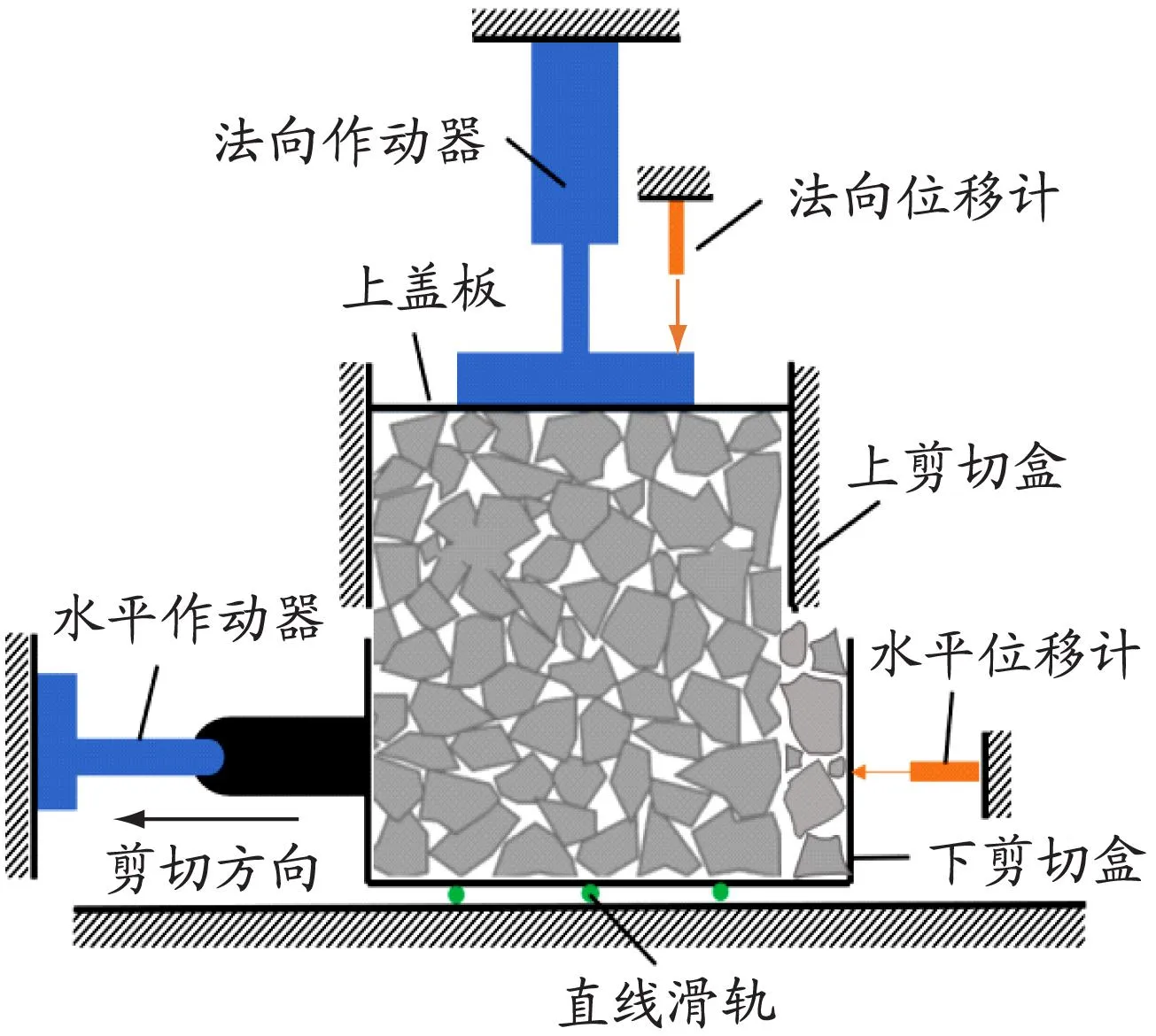
图14 大型直剪仪示意

法向载荷分别为20、50和100 kPa时,室内直剪试验与离散元模拟的剪切应力-剪切应变对比曲线见图15,可知在剪切过程中,基于多面体单元建立的直剪离散元模型的剪切应力-剪切应变曲线与室内试验结果基本吻合。因此,当离散元模型参数选择合适时,多面体离散元法能较准确地模拟碎石颗粒的剪切特性。

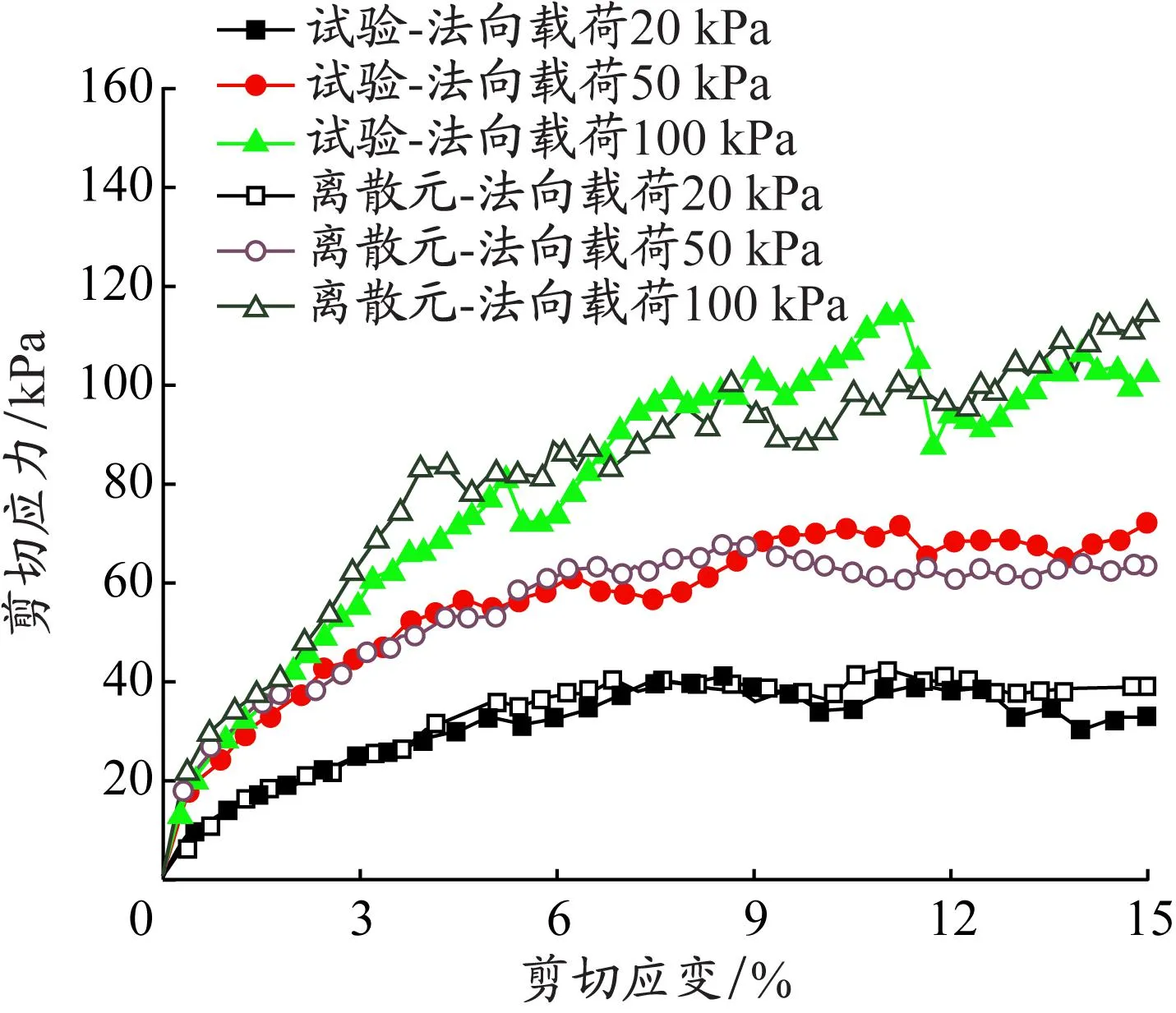
图15 不同法向载荷条件下剪切应力-剪切应变曲线

当法向载荷分别为20、50和100 kPa时,取剪切应力-剪切应变曲线上的峰值为抗剪强度。其中室内直剪试验的抗剪强度分别为41.15、73.66和114.14 kPa,离散元模拟的抗剪强度分别为42.81、68.21和121.44 kPa,对应的相对误差分别为4.03%、7.40%和6.40%,表明多面体碎石单元可以合理模拟碎石颗粒,且在较小误差下表达其抗剪特性。

由于碎石颗粒的离散特性,颗粒间几乎无黏结,碎石剪切强度的变化规律不能简单地用线性的摩尔库伦强度准则表征。本文采用INDRARATNA等[25]提出的非线性强度准则对碎石强度进行分析,即:

(18)

式中:τp为碎石颗粒的抗剪强度;σn为法向载荷;σc为碎石母岩的单轴抗压强度,本文取130 MPa[26];a、b均为无量纲的拟合参数。

采用式(18)对碎石颗粒的抗剪强度与法向应力的非线性关系进行拟合时,考虑3个有效散点确保基于幂函数拟合的有效性。正则化后碎石剪切应力比与法向应力比关系的离散元模拟结果及试验结果见图16。可以看出,采用幂函数拟合获得的离散元模拟和试验的拟合优度R2均大于0.98,说明此函数能较好反映碎石颗粒的非线性剪切强度。

图16 正则化后碎石法向应力比与剪切应力比关系的离散元模拟结果及试验结果

4 结 论

本文结合三维激光扫描技术获取碎石颗粒真实的表面几何形貌,构造碎石颗粒任意形态多面体单元。为探究该类多面体单元在模拟碎石颗粒力学性能上的有效性,进行了碎石颗粒的休止角和直剪离散元模拟,并将离散元模拟结果与室内试验的结果进行对比,有以下结论:

(1)多面体单元可以合理地表达真实碎石颗粒的棱角特征和凹凸特性,能较准确地复刻碎石颗粒的自然形态。

(2)本文建立的碎石休止角数值模型能合理模拟碎石的流动特性,并获得碎石颗粒的休止角,计算结果可以指导碎石的现场施工、运输和堆积储存。多面体碎石直剪数值模型的剪切应力-剪切应变曲线和剪切应力比与法向应力比关系同试验结果能较好吻合,表明多面体离散元模型能有效表达碎石颗粒材料的剪切特性。

本文的研究结果为模拟碎石等非规则颗粒材料提供新的思路和参考,可通过多面体单元建立相关的离散元力学模型,探究非规则颗粒材料的复杂力学性能。