基于空间平均效应修正的水听器校准方法研究

鲁宗蕊, 钱飞明, 邢广振, 陈 洋, 杨 博

(1.北京化工大学 信息科学与技术学院，北京 100029；2.哈尔滨工业大学 仪器科学与工程学院，黑龙江 哈尔滨 150006；3.中国计量科学研究院，北京 100029； 4.广州大学 机械与电气工程学院，广东 广州 510000)

1 引 言

近年来,随着超声医疗器械在国内外市场的高速发展,医疗超声辐射剂量的准确性备受关注。根据国际标准要求,医用超声设备的声输出参数需在规定的安全范围[1～3]。水听器作为测量医用超声参数的标准器,对其灵敏度的准确评价相当重要。

目前,水听器灵敏度的校准方法有很多种,如互易法[4]、时间延迟谱分析法[5]、基于光学干涉测量法[6]、比较法[7]等。相较于其它校准方法,比较法操作简单,可实现水听器的快速校准。然而,由于水听器的空间平均效应,引起水听器灵敏度校准误差增大。水听器的灵敏度对超声在水中传播的非线性信号表现出很大的频率依赖性,非线性信号谐波的声束宽度随频率增加而减小[8～12],当谐波的声束宽度变得与水听器敏感元件的尺寸相当或更小时,水听器灵敏度的校准会受空间平均效应[13]的影响。

为了解决水听器空间平均效应的问题,国内外学者对其进行了研究。Wear基于高斯分析法对声场进行表征,通过声场与水听器有效面积的积分提出适用于矩形场的空间平均效应修正模型[14];Radulescu等人基于焦平面声场引入“焦数”提出适用于高频非线性的修正模型[15,16]。结果显示,修正误差都得到显著改善,但模型对声场具有相对的局限性。Zeqiri和Bond通过扫描声场的剖面轮廓曲线推导修正系数建立适用于多种声场的修正模型。为了获得更精细频率间隔下的修正,本文基于脉冲扫描法推导出声场声束宽度与水听器有效直径关系,建立空间平均效应模型。

为了高效获取更精细频率间隔下的水听器灵敏度,本文利用声场扫描法对水听器进行比较法校准,通过脉冲扫描声场的声束宽度和水听器有效直径获得空间平均效应修正值,经实验测量对比修正前后结果。本文提出比较法校准原理以及校准水听器的空间平均效应修正模型;介绍校准实验装置,对待校水听器进行校准和修正分析;进行不确定度分析,最后给出结论。

2 基本理论

2.1 校准方法

水听器的开路灵敏度定义为水听器输出端开路电压U0和声场中放置水听器前存在于该点的自由场声压p之比[17]:

(1)

比较法校准水听器的校准原理是基于两个水听器在相同位置对同一自由场声压测量的实验条件进行。首先使用标准水听器对声场测量输出电压信号Uref,将标准水听器取出,放置待校水听器在相同实验条件下测量输出电压信号U,可推导出待校水听器的灵敏度M的关系表达式:

(2)

标准水听器的灵敏度Mref可通过基于激光外差法[18]测量获得。由于待校和标准水听器的有效直径不一致,其引入的空间平均效应会引起灵敏度误差增大,因此需对比较法校准水听器的结果进行修正。

2.2 空间平均效应修正

为了评估空间平均效应,需对超声场进行分析。由于非线性传播,声压场的第n次谐波分量表达式为[19]:

(3)

式中:r表示水听器测量平面的径向坐标,该平面垂直于声波传播方向;f1表示基波频率;s(nf1)表示传播轴上第n次谐波的相对声压;wn(r)表示第n次谐波声场与x、y之间的关系。第n次谐波的声场对x、y的依赖关系可以近似为两个高斯函数的乘积[20]:

wn(x,y)=wnx(x)wny(y)

(4)

式中,wnx(x)、wny(y)分别表示:

(5)

(6)

这里,gnx、gny分别表示相位对x、y的依赖关系。高斯参数σnx、σny分别表示声束剖面在横向和纵向的宽度。对于轴对称声源,gnx=gny=gn、σnx=σny=σn,通过实验[21,22]研究分析,谐波波束宽度σn与谐波序数的关系为:σn≈σ1/nq,对于超声诊断、轴对称场已测量q值接近0.8。此外,σn可通过水听器对xOy面扫描声场进行估计。

当σnx=σny=σn时,忽略相位的影响,则第n次谐波下的归一化声压幅值为:

(7)

水听器的空间平均效应受其敏感元件有效尺寸的影响,该有效尺寸依赖于水听器的指向性响应,指向性响应描述为频率响应对应入射角的函数。它描述了要准确测量声压时精确水听器角度方位的关键,它的测量可用于确定水听器敏感元件的有效尺寸。

入射在水听器上的声压场可以分解为入射在敏感元件上的平面波的角谱。对于正常入射的平面波,空间平均为零,但随着入射角的增加,就会引起空间平均效应。实验研究表明,通过在假定“有效”敏感元件尺寸的水听器表面的自由场(即不存在水听器的情况下)上可精确预测空间平均效应。有效半径a(f)依赖于频率,区别于标称(几何)半径ag。水听器的有效半径a(f)可通过实验测量,也可通过经验公式进行计算。在本文中,未测量其指向性响应,使用经验公式进行评估[23]:

(8)

式中:ag是水听器的标称半径(为物理尺寸);f是频率(单位为Hz);a(f)是水听器的有效半径;ag和a(f)的单位均为mm。

通过对非线性声场的声压幅值与水听器有效半径a(f)进行卷积积分,可得空间平均效应修正的物理表达式[24]:

(9)

对式(9)经数值分析后进行曲线拟合,可推导出空间平均效应修正的经验公式:

(10)

式中:σn(f)表示各频点对应的-6 dB声束直径,可通过对超声换能器在非线性声场中进行平面扫描获得。

通过式(10)分别对标准水听器和待校水听器进行计算,可得相应的修正系数δref、δ:

(11)

(12)

式中:ag1、ag2分别表示标准水听器和待校水听器的标称半径。在比较法校准中加入这两个修正系数,可得关系表达式:

(13)

进而可求出空间平均效应修正值Δδ:

(14)

将空间平均效应修正值Δδ代入式(2)可得比较法校准水听器的空间平均效应修正模型:

(15)

3 实验研究

3.1 实验装置

比较法校准水听器灵敏度实验系统示意图如图1所示。校准系统包括去离子水箱、脉冲发生器、超声换能器、水听器、步进电机控制系统、示波器和计算机控制系统。该系统中计算机控制系统通讯,驱动电机可实现声场扫描。脉冲发生器发出电压脉冲信号激励到超声换能器,水听器将接收的超声信号转换为电压信号,经示波器显示、采集后传输至计算机,供系统存储、分析、记录。

图1 水听器校准系统示意图

3.2 实验结果分析

在去离子水箱中,对标称直径0.2 mm的水听器在不同频率范围内进行比较法校准实验,并将校准结果与证书值进行对比,结果分析如下:

首先,设置脉冲发生器的脉冲宽度为25 ns,超声换能器的标称中心频率为20 MHz。使用标称直径1 mm的标准水听器进行声场测量输出电压信号,对其进行FFT变换得到频谱图;之后,将标准水听器取出用待校水听器进行替换,采集、保存水听器的输出电压信号,对其进行频谱分析,结果见图2。

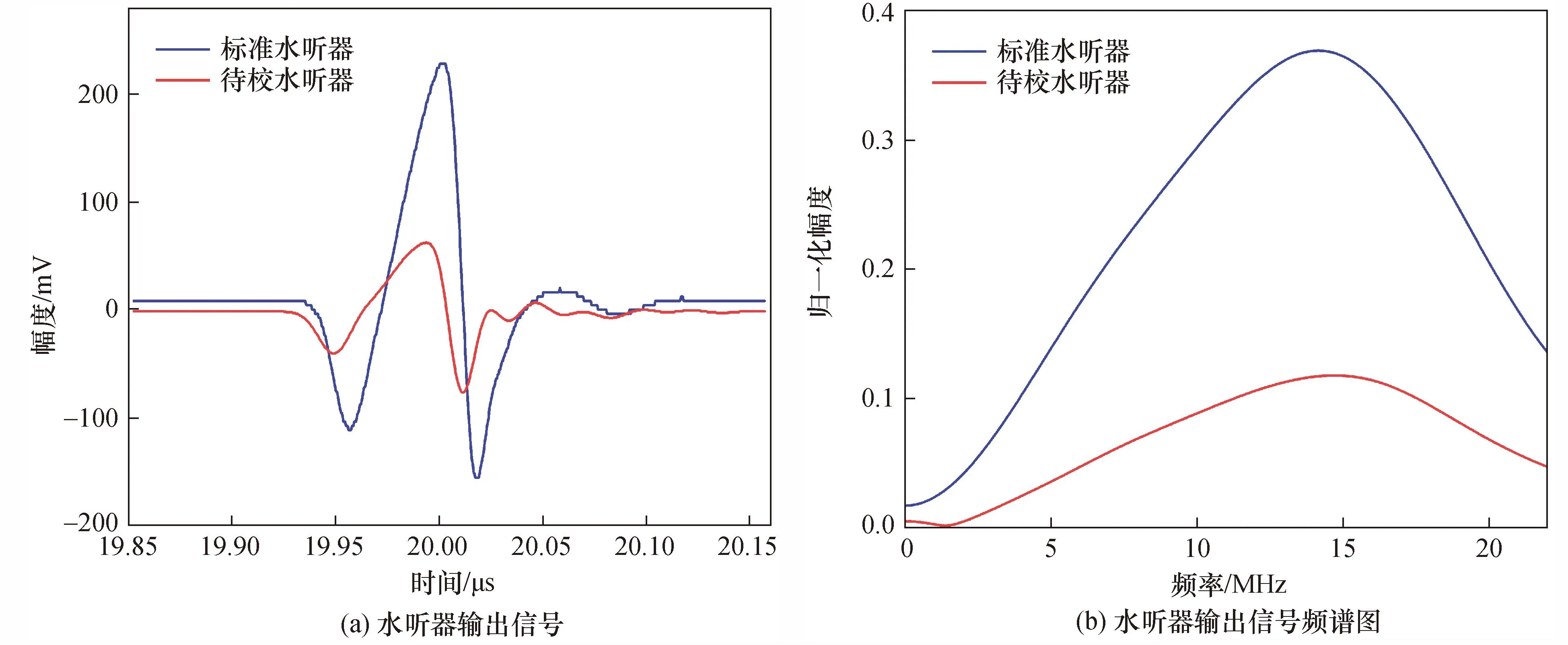
图2 水听器输出电压信号及其频谱图

将标准水听器和待校水听器的输出电压代入式(2)即可得到待校水听器灵敏度。

为研究水听器孔径的空间平均效应,需对声场进行分析。使用标称直径0.5 mm的水听器进行声场扫描,得到0.5～20 MHz(频率分辨率为0.05 MHz)频率下的声束宽度。图3分别给出在5、10、15、20 MHz频率下声场扫描结果,可以看出随着频率增加,声束宽度逐渐减小,对待校水听器灵敏度将产生误差。

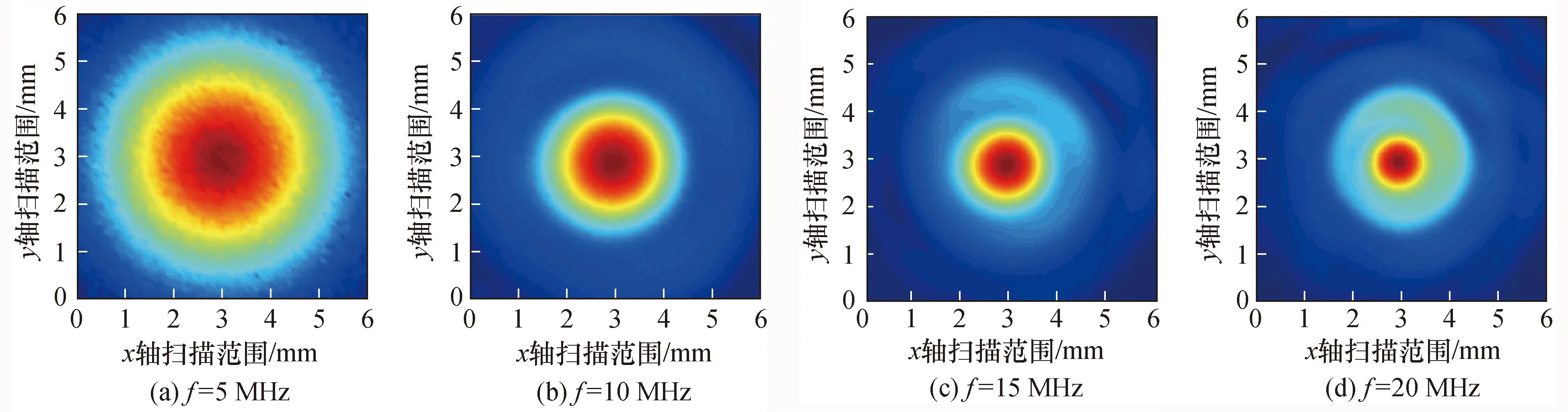
图3 0.5 mm直径水听器扫描结果

为了修正空间平均效应所引起的误差,引入修正系数进行校准,结果见图4。

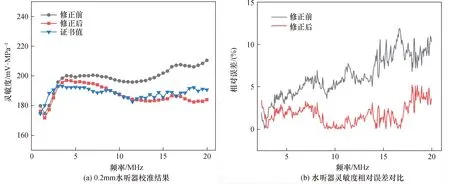
图4 0.2 mm水听器空间平均效应修正前后的结果对比

图4(a)为待校水听器修正前后比较结果,频率覆盖范围为0.5～20 MHz。图4(b)为修正前后相对误差对比。

以5～20 MHz(频率分辨率为1 MHz)为例,进行各频率下水听器灵敏度分析,结果见表1。

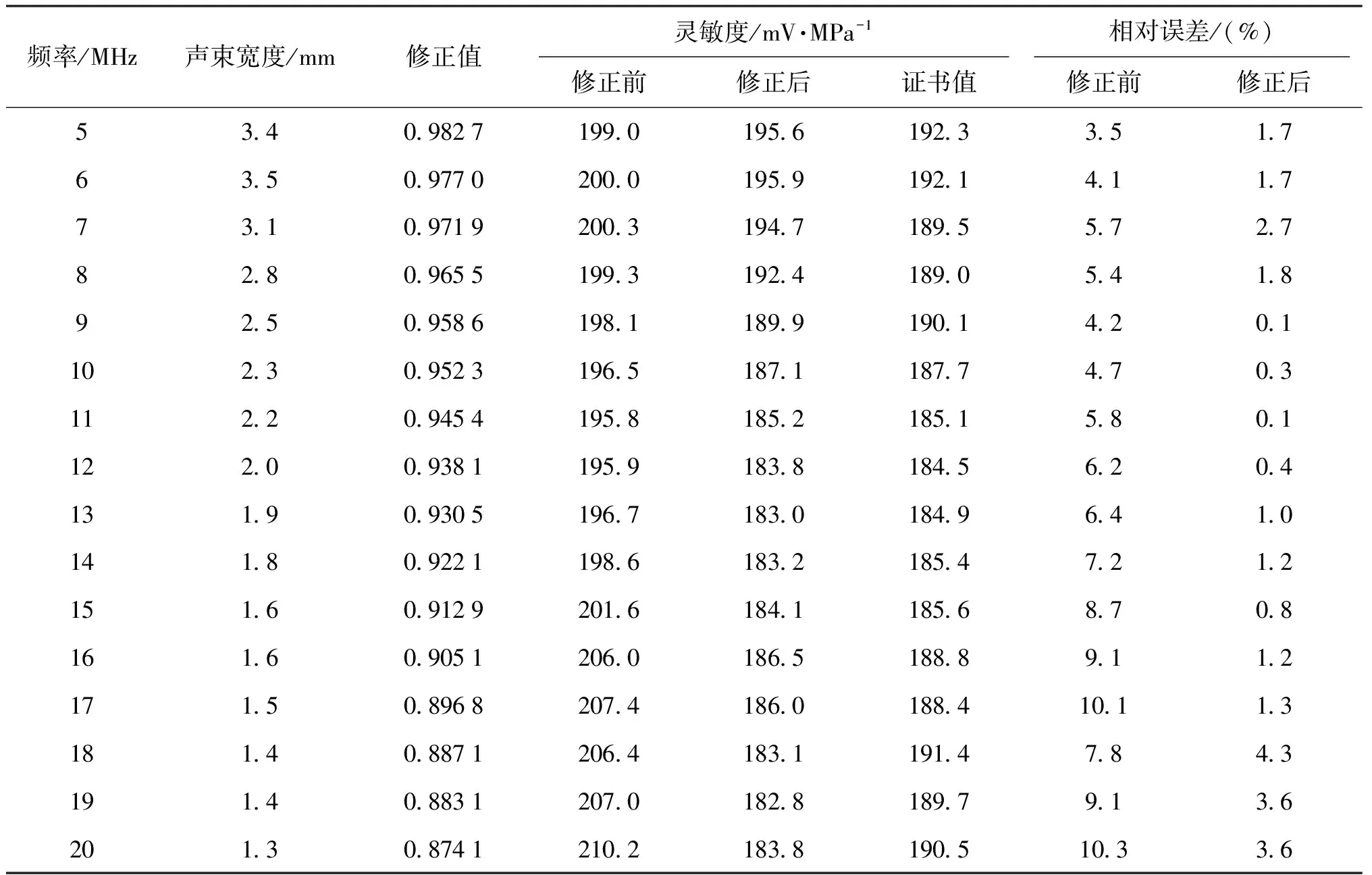
表1 各频率下空间平均修正前后的水听器校准灵敏度与检测证书值的比较

可以看出,本文基于空间平均效应修正的校准方法对水听器的校准结果与证书值有良好的一致性,该方法使相对误差从7.1%降至3.0%(取各频点下相对误差的平均)。

4 测量不确定度评定

测量不确定度包含A类不确定度和B类不确定度。由重复性测量引起的为A类不确定度,其他采用B类不确定度,后者与系统误差有关。

4.1 A类不确定度评定

在由重复性引入的A类不确定度研究中,通过对待校水听器在各频点下进行6次独立测量,采用贝塞尔公式计算标准偏差:

(16)

可获得各频点下的A类不确定度,计算结果见表2。

4.2 其他不确定度评定

4.2.1 标准水听器

使用比较法校准水听器时需标准水听器作为基准,标准水听器的灵敏度是基于激光外差法获得,且标准水听器的测量不确定度给定范围为:<15 MHz时为0.5 dB;≥15 MHz时为0.6 dB。具体结果见表2。

4.2.2 水听器输出端电压测量

水听器输出端电压信号由示波器采集得到,示波器采样误差引入的不确定度由其校准证书获得。当耦合阻抗设置为50 Ω时,根据示波器的通道校准证书,可计算接收通道电压测量的不确定度,结果见表2。

4.2.3 水听器空间平均效应修正

在非线性声场中,随着频率增加,声束宽度逐渐减小,水听器的空间平均效应更加严重。在进行修正时,通过测量的声束宽度与水听器有效直径可拟合修正结果。该效应修正的不确定度主要来源于各频点下水听器的有效直径和声束宽度的测量。通过对各频点下声束宽度进行独立重复测量,计算得到不确定度,计算结果见表2。

4.2.4 水听器共位置

比较法校准水听器要求待校水听器与标准水听器在同一位置,即在声轴上到超声换能器的距离相等。实验过程中通过示波器的光标测量得到时间差Δt,可计算标准水听器到超声换能器的间距,进而可定位待校水听器的位置。不确定度主要来自对声波波形特征点的选取。在对水听器多次测量的实验中发现,这种保证光标测量时间差相等的方法对水听器灵敏度引起的不确定度很小,并已包含在A类不确定度评定中。

4.2.5 对准误差

测量点对准误差来自水听器与超声换能器对准角度,通过测量XZY轴向偏移中心处的质点振速可获得,计算结果见表2。

4.2.6 水温

水听器灵敏度受温度的影响,根据英国NPL研究,水听器的灵敏度温度系数为(0.61±0.08)%。因此,采取分辨力为0.1 ℃下的温度计测量去离子水,将水听器的温度统一修正到规定温度(20 ℃)下。则温度对水听器灵敏度的影响取决于温度计的分辨力,不确定度小于0.1×(0.61±0.08)%,可忽略不计。

4.3 合成不确定度和扩展不确定度

对上述相对不确定度分量,用

计算合成标准不确定度,假设不确定度满足正态分布,取包含因子k=2,则扩展不确定度为U=k·uc,计算结果见表2。由表可知,标准水听器作为基准的测量不确定度低于待校水听器的测量不确定度;与待校水听器的证书测量不确定度(<15 MHz,1 dB;≥15 MHz,1.5 dB)相比,基于空间平均效应修正的水听器校准方法在高频时具有更小的测量不确定度(低频是由于信噪比过低所引起的);不确定度最大为1.3 dB(未给出频点的不确定度均小于该值)。

5 结 论

针对比较法校准水听器时空间平均效应所引起灵敏度误差增大这一问题,本文提出了一种基于空间平均效应修正的校准方法。通过对脉冲声场的扫描获得声束宽度,推导与水听器有效直径之间的关系,进而拟合出空间平均效应修正模型。通过引入修正模型的校准方法,对标称直径0.2 mm的水听器进行了实验验证。经实验获得修正后的水听器灵敏度更接近证书值,在高频(>15 MHz)时表现显著,且比修正前的平均相对误差减小了4.1%,验证了修正模型的有效性。通过对待校水听器进行不确定度分析,可得测量不确定度为1.3 dB(k=2),实际校准时,多个频点的测量不确定度在1.3 dB(k=2)范围。值得一提的是,在低频范围,由于系统信噪比过低,修正后的校准结果变化不明显,后续将对该影响进行深入研究。