基于数值模拟的隧道爆破振动对石刻文物的安全性评估

林 生 凉

(福建省建筑设计研究院有限公司,福建 福州 350001)

随着我国经济建设的不断推进,公路等交通运输基础设施的建设方兴未艾,其中公路隧道是工程关键组成部分。公路隧道常采用爆破法施工,但爆破所产生的振动不可避免地对邻近的构筑物产生负面效应[1-2],尤其我国历史遗迹非常丰富,当拟建隧道口处存在历史遗迹等文物时,爆破开挖甚至会导致其损毁,造成历史价值流失。因此,在工程建设中有必要开展隧道爆破振动对历史遗迹等文物的安全评估。

当前,众多学者已开展了隧道爆破振动对邻近建(构)筑物影响的研究。如赵勇等[3]基于无限元边界的动力数值模型研究了输水隧洞爆破振动对周边高压输电铁塔的安全评估与优化措施;李广伟[4]探究了新建隧道爆破施工对已有隧道的影响;李波等[5]则借助LS-DYNA动力数值模拟方法分析了不同爆破施工后行洞对先行洞的影响;张黎明等[6]探讨了爆破振动对地下管道安全的影响;肖欣欣等[7]研究了输电高压铁塔受到隧道开挖及爆破影响,提出了避免地表铁塔塔基失稳塌陷的措施。马文瀚等[8]借助数值模拟研究了爆破振动对地质遗迹的影响。由于数值模拟可较好地解决爆破振动时各类边界条件下的问题,且能够解析出爆破振动时结构的动力响应特征,因而被广泛应用于爆破振动研究之中[2,9]。

鉴于此,本文以福州市福泉高速公路连接线拓宽改造工程为依托,以保护石刻文物的完整性和降低工程爆破施工风险为目标,基于有限元数值模拟分析,研究爆破荷载下隧道洞口石刻文物的动力响应特征,开展爆破施工方案的安全性评估。

1 拟建隧道与摩崖石刻文物概况

拟建城门山隧道位于福州市福泉高速公路与三环快速路互通东南角。城门山隧道起讫桩号FDHK1+885—FDHK2+385,全长500 m,属于短隧道,隧道洞宽17.40 m,洞高11.40 m,隧道洞顶最大埋深约为67 m。隧道区域地势具有一定起伏,场地现状地面整体高程约在罗零6.860 m～87.220 m左右,地貌单元为丘陵地貌及冲积平原,下部主要为燕山晚期不同风化程度的侵入花岗岩层。

拟建隧道岩体开挖方式主要有爆破开挖围岩与静力裂解法开挖围岩两种方式。由于距离隧道下方福州地铁6号线较近,里程号为FDHK2+300—FDHK2+385段隧道优先考虑采用静力裂解方式开挖。剩余里程号为FDHK2+220—FDHK2+300段隧道则采用爆破方式开挖。

狮头山摩崖石刻位于福州市魁浦大桥东侧以及福泉高速南侧的狮头山东北坡,3处摩崖石刻文物位于罗零高程19.5 m～30.0 m斜坡上出露的三块孤立岩石,始建于清朝,由“锦绣谷榜书”、“第一山榜书”以及“林瀚题记”等遗产要素构成。狮头山体呈圆缓型,属剥蚀残丘地貌,地形坡度为20°～25°,局部约30°,山坡浅表层覆盖残积层,多见花岗岩基岩出露,山体多有早期开采岩石形成的陡坎、陡坡,自然山坡植被较为茂密,残丘最高点罗零高程为108 m。

图1即为狮头山摩崖石刻与拟建隧道相对位置工程地质平面示意图和全景照。由图1可知,3块摩崖石刻位于拟建城门山隧道的出口处附近,周边可见基岩出露,石刻附近斜坡前期被改造成多级种植平台,高1.5 m～3.0 m,用石刻堆垒形成台阶状种植地。其中,1#石刻岩体与隧道洞顶垂直距离约为12.34 m,距离隧道洞门仰坡坡顶线约为6.43 m;2#摩崖石刻位于隧道洞顶上方,石刻岩体与隧道洞顶垂直距离约为11.82 m,距离隧道洞门仰坡坡顶线约为2.57 m。3#摩崖石刻则位于隧道洞口外侧路堑边坡之上,与边坡线距离约为1.12 m。同时,现场调查表明,1#、2#摩崖石刻古迹在现状情况整体处于稳定状态。但是,由于该石刻北侧存在外倾临空面,在受外来施工爆破振动、重力作用下存在向北侧倾覆的危险性。3#摩崖题刻文物为一块中型孤石,其本体下部有强风化岩夹层,已具有变形移位的迹象。

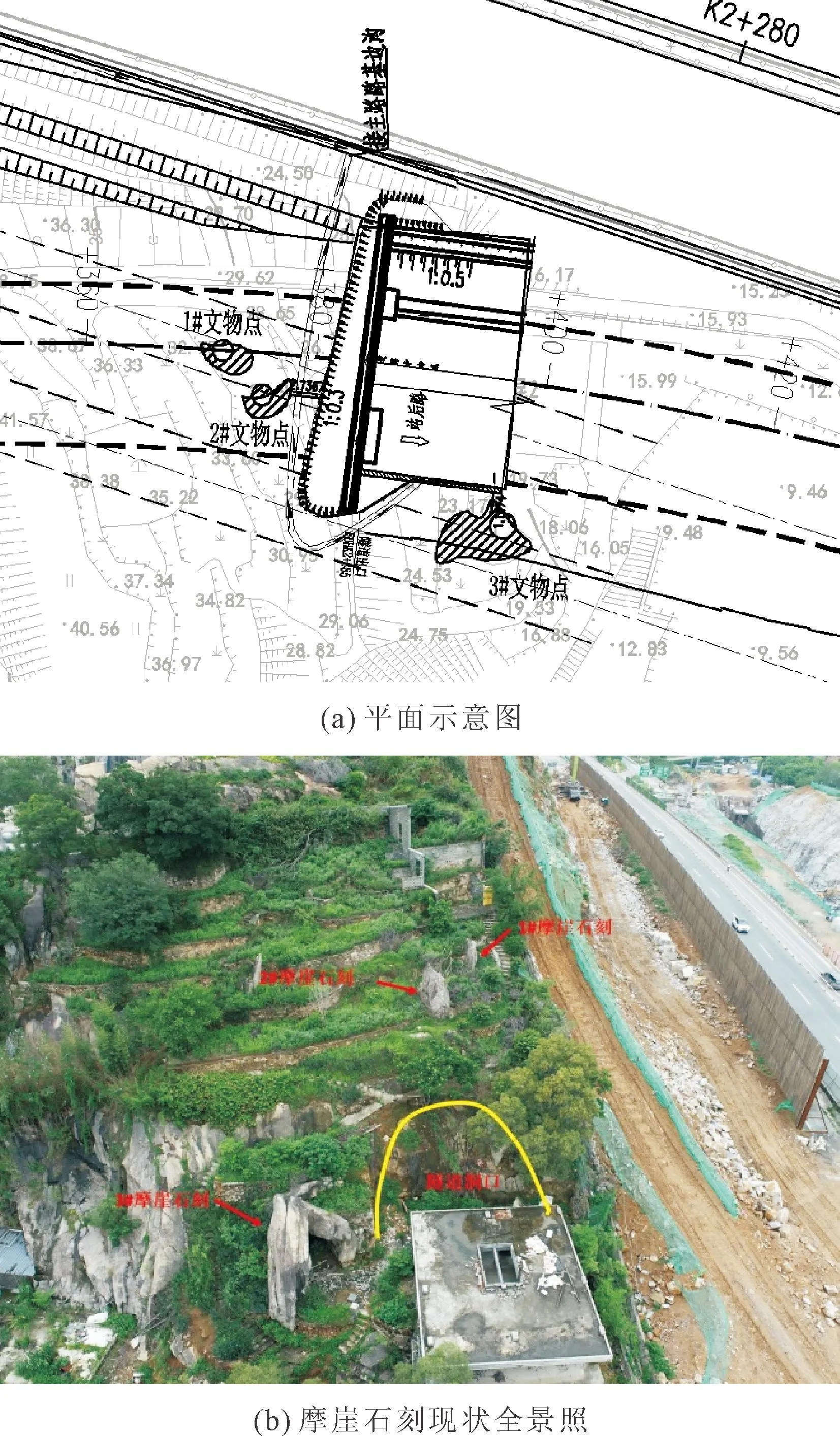
图1 狮头山摩崖石刻与拟建隧道相对位置

2 三维数值模型的构建

2.1 模型尺寸与网格划分

为掌握城门山隧道工程爆破施工过程对三处摩崖石刻文物的影响,拟以采用爆破方式开挖的隧道段FDHK220—FDHK300为研究对象,根据实际地形、地质条件,采用有限元软件Midas GTS NX建立起纵向215 m,横向145 m,高60 m～145 m的有限元模型,如图2所示。该数值计算模型中岩土体采用四面体实体单元进行模拟,公路隧道与地铁隧道则采用三角形板单元模拟。计算模型中节点总数为19 330个,单元总数为111 743个,如图3所示。

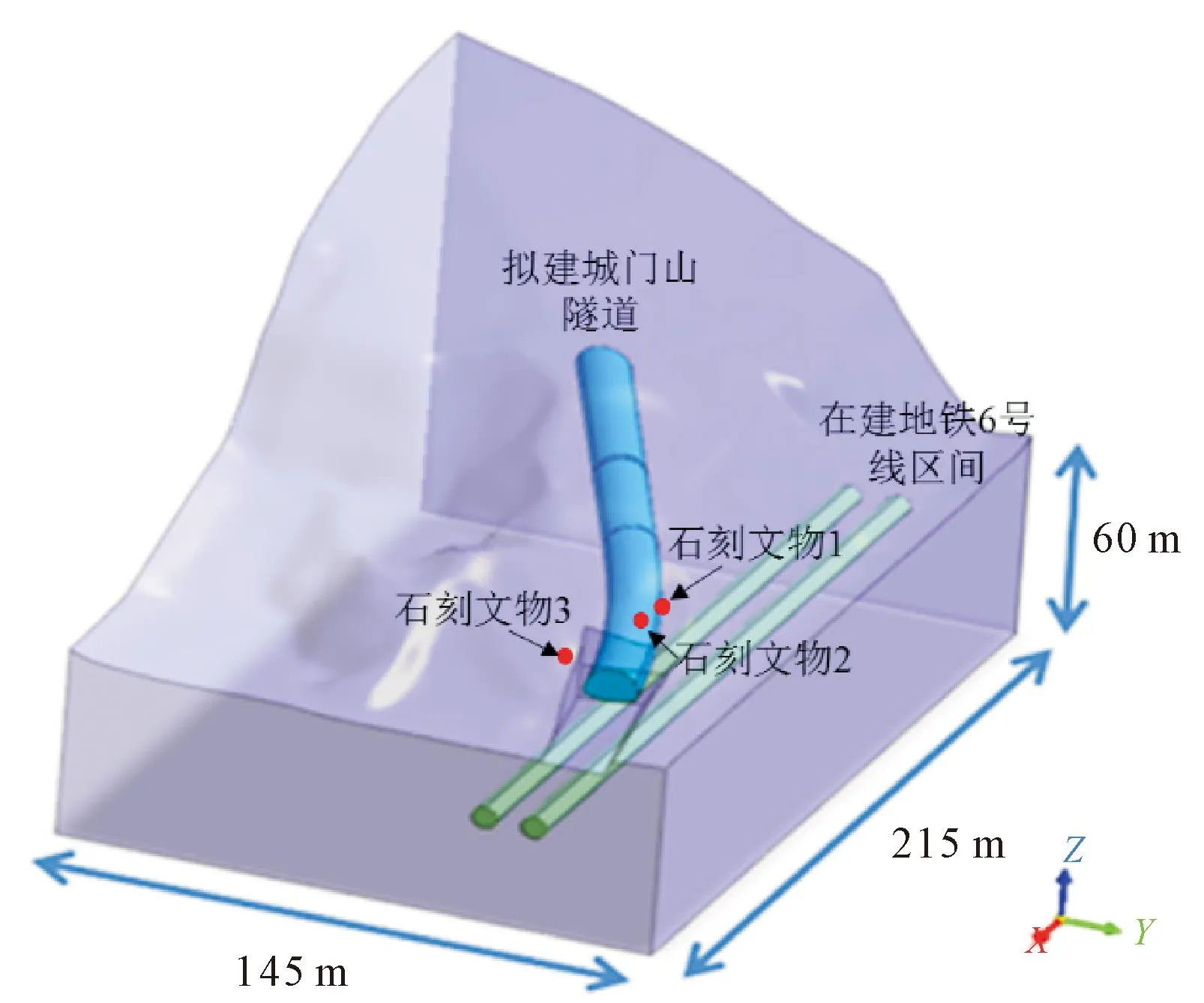
图2 三维数值模型

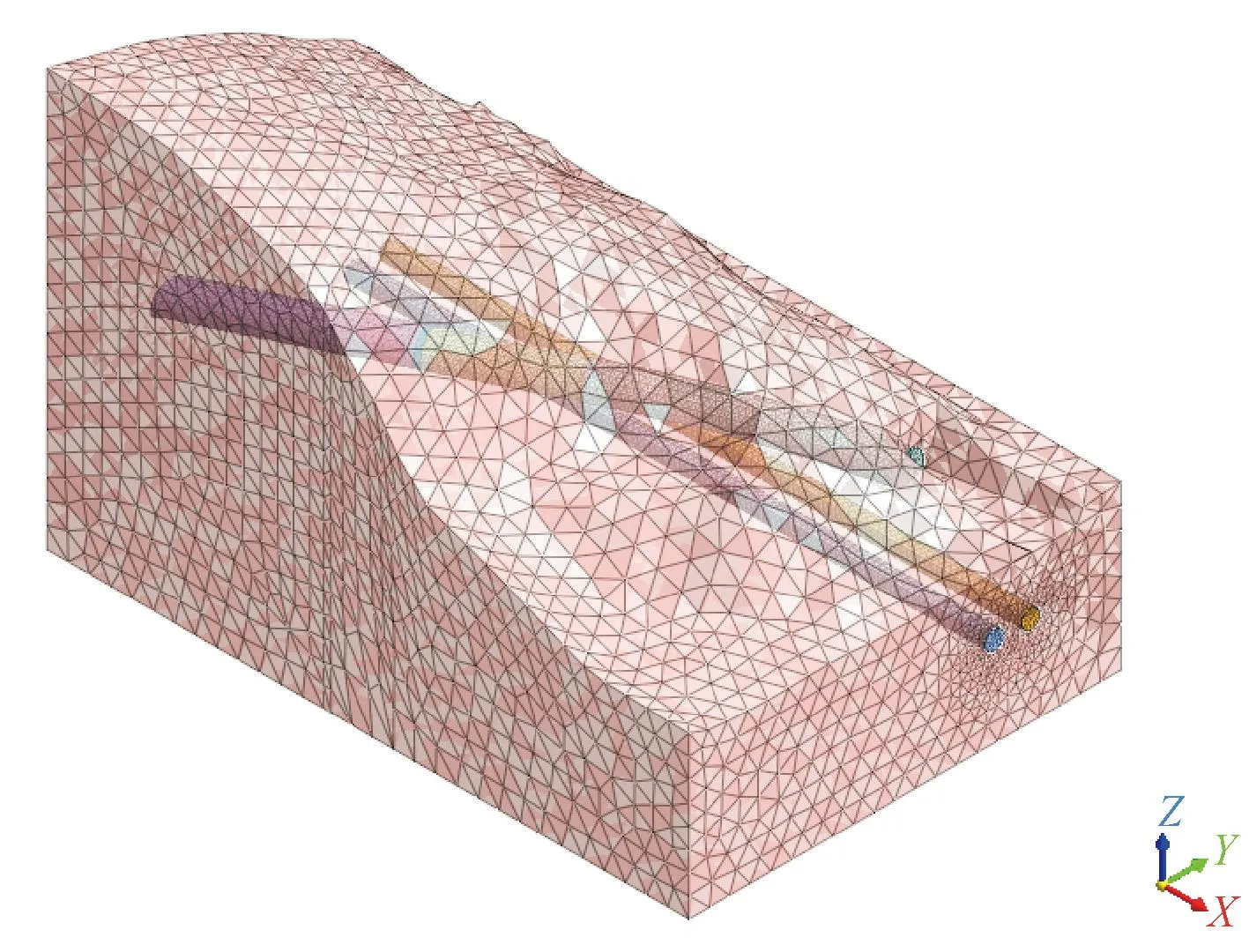
图3 数值模型的网格划分

2.2 计算参数

有限元计算中所采用的参数主要来源于工程勘察报告中所给的建议值。采用Midas软件内嵌的Mohr-Coulomb弹塑性本构模型模拟地层岩土体的应力应变特性。Mohr-Coulomb强度理论能较好地描述岩土材料的强度特性和破坏行为,在岩土工程领域得到了广泛的应用。表1即为相应的岩土体计算参数。此外,公路隧道衬砌及既有地铁隧道衬砌均采用刚度较大的钢筋混凝土管片,可将其视为弹性材料,参照《混凝土结构设计规范》[10](GB 50010—2010),则相应的计算参数如表2所示。

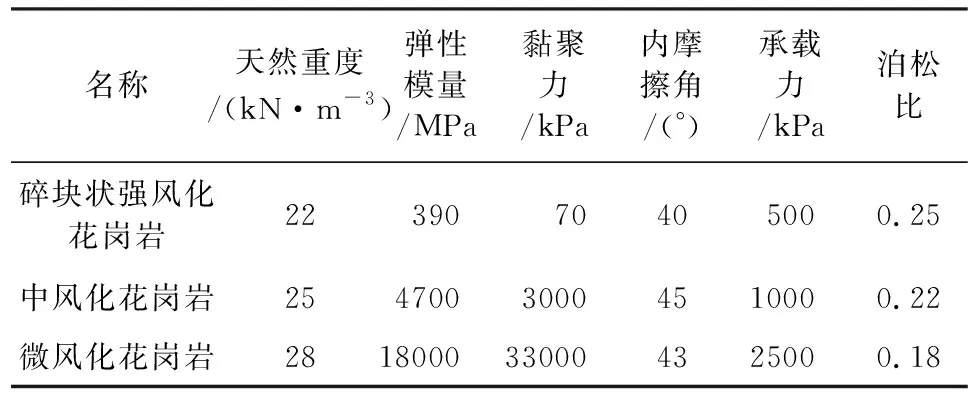
表1 岩土体计算参数

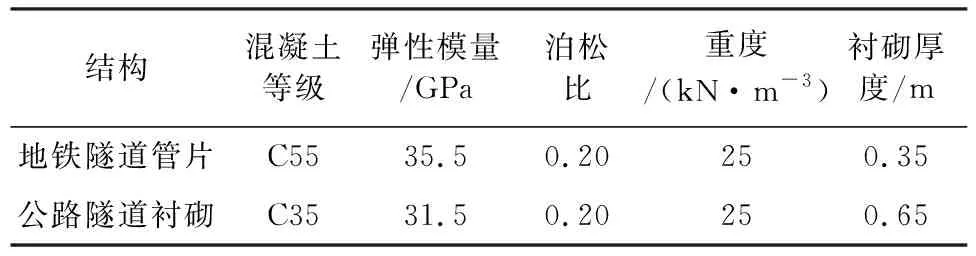
表2 结构单元计算参数

2.3 爆破荷载计算工况

采用有限元法分析爆破振动影响的关键工作在于建立爆破加载模型,包括确定爆破激振力的大小、作用位置和方向、峰值时刻和持续时间等。基于此,根据计算和爆破的实际情况,作以下假设:

(1) 爆破荷载以压力形式的均布荷载作用在隧道壁上,方向垂直于隧道洞壁。

(2) 根据经验公式和振动测试的监测结果,爆破荷载计算时间取1.0 s。

爆破作用荷载采用美国National Highway Institute提出的公式[11],每1 kg炸药的爆破压力为:

PB=0.45ρV2/(1.0+0.0008ρ)

(1)

式中:PB为1 kg炸药在爆破孔壁上产生的最大爆破压力;ρ为炸药密度,取1.0 g/cm3;V为炸药爆速,取3000 m/s。

式(1)决定的是爆破发生时的最大爆炸压力。但实际上作用于孔壁上的动压力是随时间变化的,通常取为指数型的时间滞后函数。根据计算经验和工程实践,拟采用的时程动压力公式为:

(2)

式中:PD为每1 kg装药量的动压力,MPa;B为荷载常量,取16 338;t为爆破荷载作用时间。

联合式(1)与式(2)可知,每千克炸药在爆炸孔壁上产生的最大爆炸压力PB= 2.2×103 MPa,加载到峰值压力的升压时间为6 ms,结合爆轰波理论和爆腔膨胀理论,并根据荷载等效原理即可获得作用到隧道侧壁的爆破荷载峰值为18.33 MPa,且其时程曲线如图4所示。

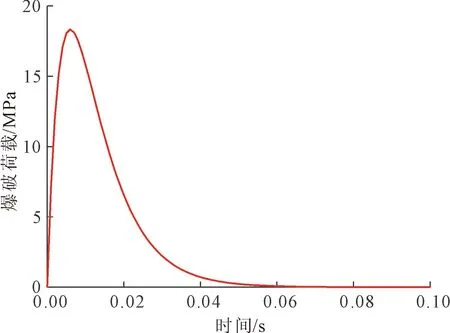
图4 爆炸荷载时程曲线

爆破振动安全允许距离可按《爆破安全规程》[12](GB 6722—2014)13.2.4的规定计算:

(3)

式中:R为爆破振动安全允许距离,m;Q为炸药量,kg;V为保护对象所在地安全允许质点振速,cm/s,按照规范,对于一般古建筑及古迹取V=0.5 cm/s;K与α为与爆破点至保护对象间的地形、地质条件有关的系数和衰减指数,考虑拟建隧道位于微风化花岗岩内,取K=150,α=1.4。

图5为爆破点位置示意图。根据现有城门山隧道施工初步方案,隧道FDHK2+220—FDHK2+260段及FDHK2+260—FDHK2+300段拟采用不同的爆破方式,则由式(3)即可反算不同工况的最大单段药量,具体如表3所示。

表3 各爆破段最大单段装药量计算表

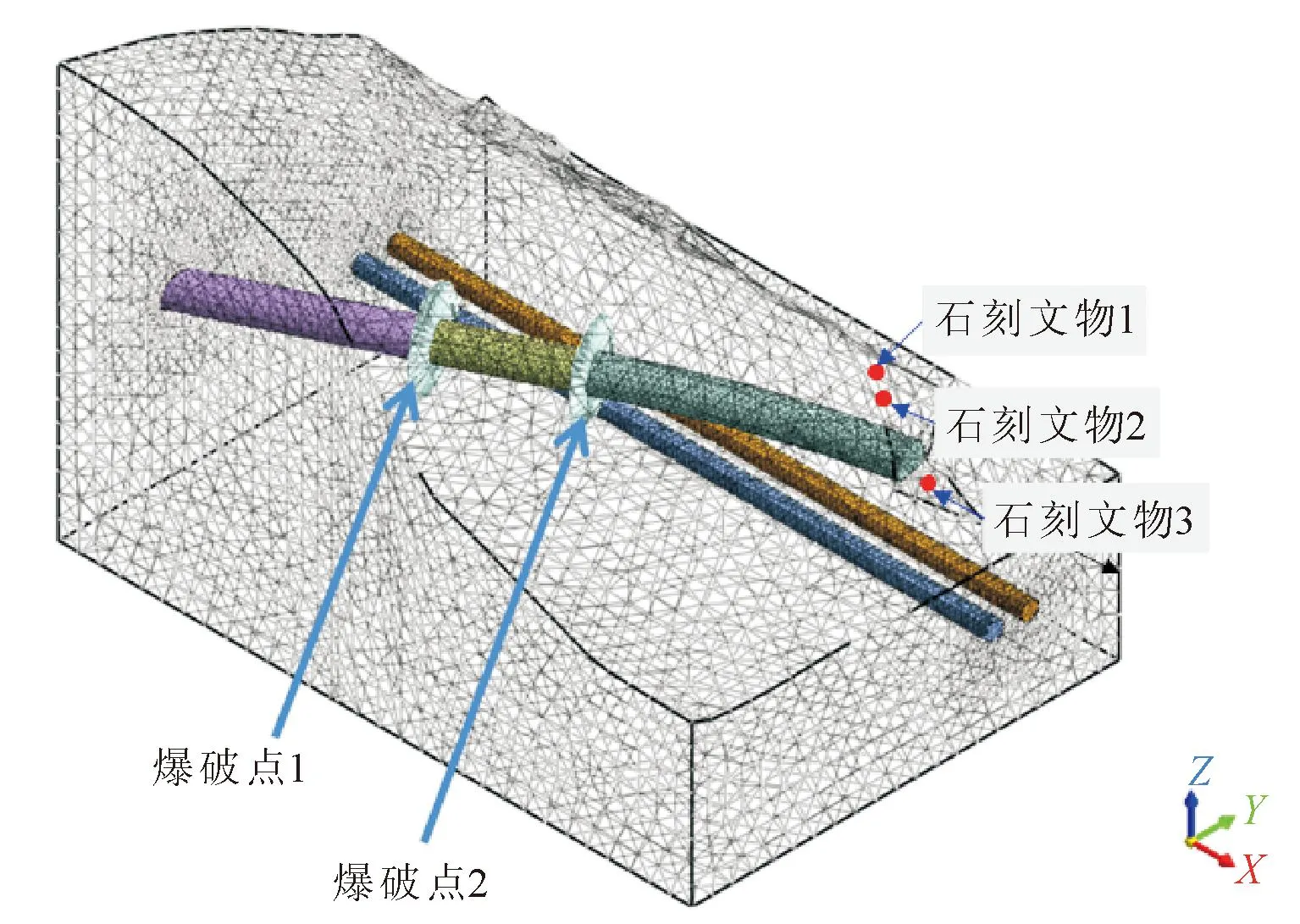
图5 爆破点位置示意图

2.4 爆破荷载作用下的阻尼边界

在对爆破荷载进行时程分析时,尚需计算模型的特征值以定义弹性边界条件。然而,弹性边界条件会由于波的反射作用而产生较大误差,为此,拟采用Lysmer粘性边界条件[13-14]。为定义粘性边界需计算模型X、Y和Z方向上的阻尼比,具体计算公式如式(4)和式(5)。而后,即可在Midas/GTS中直接通过“地面弹簧”生成粘性边界。

P波:

(4)

S波:

(5)

式中:Cp和Cs分别为P波和S波的阻尼常数,kN·s/m;ρ为岩土体密度,kg/m3;A为单元截面积,m2;λ为体积弹性系数,λ=vE/(1+v)(1-2v),其中E为弹性模量,Pa;v为泊松比;G为抗剪模量,Pa;cp和cs分别为P波和S波的单位面积阻尼常数。

3 结果分析

3.1 特征值的计算

在采用有限元法模拟岩土体动力学问题时,常采用瑞利阻尼来处理阻尼效应,瑞利阻尼模型可综合反映材料和环境对结构体系动力响应[15]。假设阻尼矩阵与质量矩阵及刚度矩阵有关,则阻尼矩阵满足:

[C]=α[M]+β[K]

(6)

式中:[C]为阻尼矩阵;[M]为质量矩阵,[K]为刚度矩阵;α、β为瑞利阻尼参数。

此时,瑞利阻尼参数可分别由式(7)和式(8)确定:

(7)

(8)

式中:ωi为岩土体数值计算模型系统的第i振型;ωj为系统第j振型;λi为第i振型的阻尼比;λj为第j振型的阻尼比。

图6即为摩崖石刻所处山体的第1阶和第2阶振型位移云图。由此可得前10阶振型周期分别为0.1758 s、0.1689 s、0.1547 s、0.1463 s、0.13435 s、0.1262 s、0.1119 s、0.1075 s、0.1030 s以及0.09836 s,取其中任意2阶周期即可计算出瑞利阻尼参数:α=2.66258,β=0.00183。获得上述参数后,便可采取时程分析法分析隧道爆破振动时的结构动力响应。

3.2 典型爆破点下摩崖石刻文物动力响应

3.2.1 FDHK2+220—FDHK2+260典型爆破点1

FDHK2+220—FDHK2+260段隧道爆破施工的计算点为爆破点1,最不利爆破点位于FDHK2+260。由表3可知,该爆破点的计算参数为最大单段药量为6.547 kg,等效爆破荷载则为119.987 MPa。

《爆破安全规程》(GB 6722—2014)给出了一般古建筑及古迹的爆破振动安全允许质点的振动速度,即0.5 cm/s。基于此,为确保摩崖石刻的安全性,选取0.5 cm/s的峰值振动速度作为隧道爆破下摩崖石刻的安全判定标准。图7给出了典型爆破点1在等效爆破荷载119.987 MPa作用下1—3号摩崖石刻文物的响应速度时程曲线。由图7可知,1—3号摩崖石刻文物的振动速度总体上呈现波动式衰减,表明采用Lysmer粘性边界条件可较好地吸收散射波,避免爆破产生的能量无法穿透固定边界而在计算模型内反复振动。

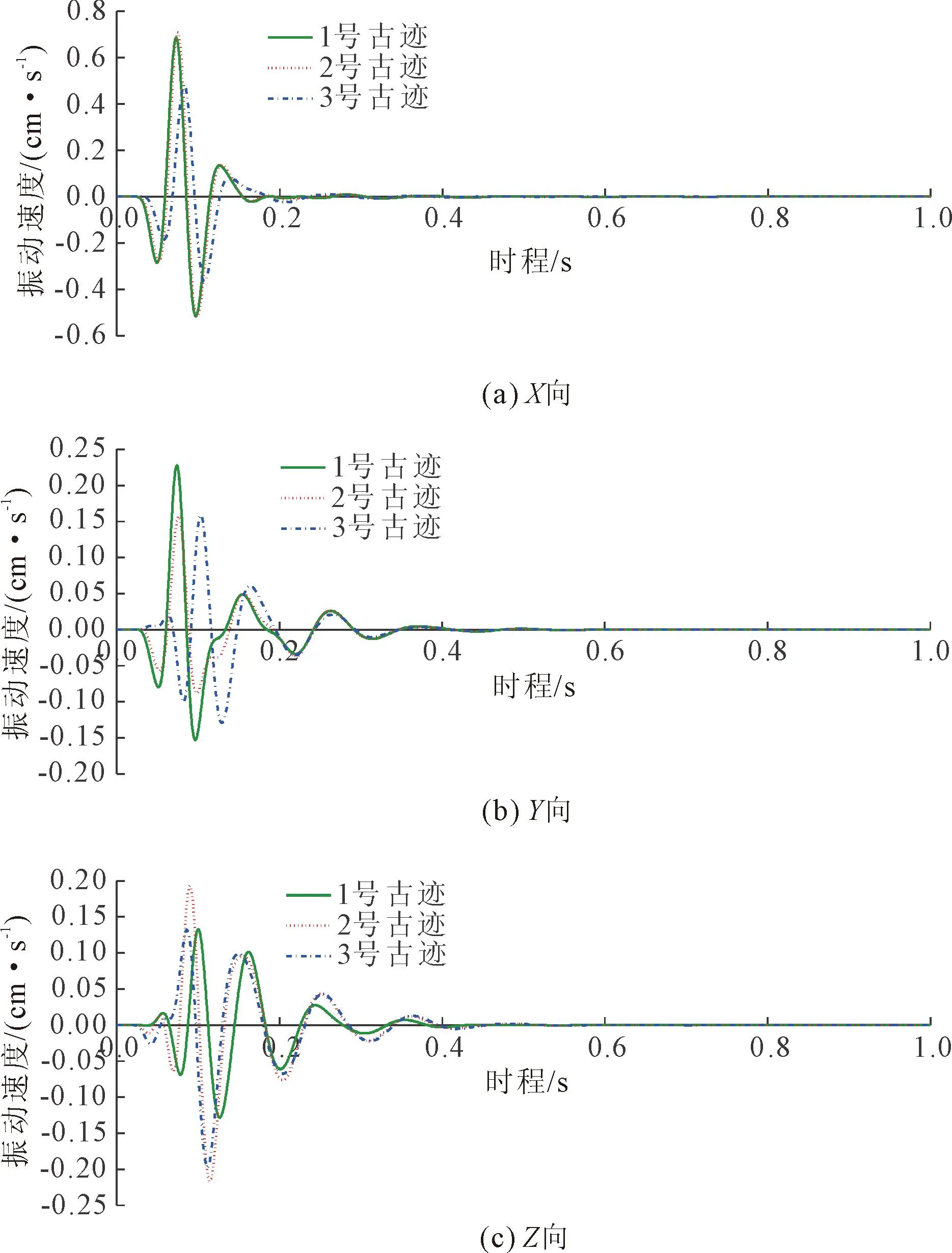
图7 爆破振动下石刻文物的响应速度时程曲线

由图7可知,1号石刻文物最大单向振动速度为0.686 cm/s,2号文物最大单向振动速度为0.710 cm/s,3号文物最大单向振动速度为0.483 cm/s。其中,1号及2号石刻文物的最大单向振动速度均大于《爆破安全规程》(GB 6722—2014)要求的最大单向振动速度0.5 cm/s,表明该施工方案不满足最大允许振速的规定。为此,在综合考虑现场的实际情况,拟将最大单段药量由6.547 kg相应减小为4.611 kg,此时隧道桩号FDHK2+260断面等效爆破荷载则由119.987 MPa相应减小为84.506 MPa。图8即为调整爆炸荷载后的石刻文物的响应速度时程曲线。

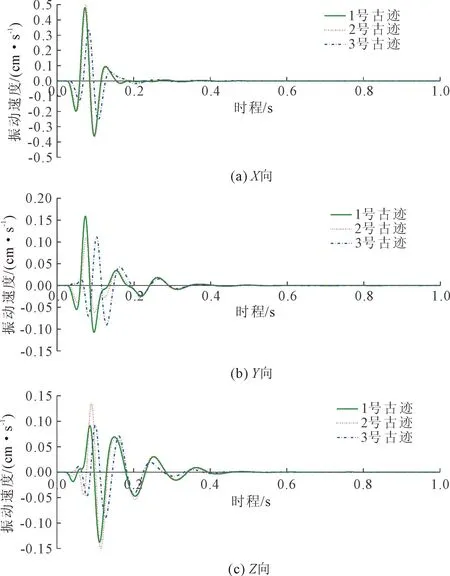
图8 调整药量后的石刻文物速度响应时程曲线

显然,由图8可以看出,在减小炸药药量后,1号与2号石刻文物在X方向的响应速度时程曲线基本吻合,且三处文物X方向的振速与衰减程度均大于Y向与Z向,但X方向的振动持续时间却小于其他两个方向。其中,1号文物最大单向振动速度为0.480 cm/s,2号文物最大单向振动速度为0.497 cm/s,3号文物最大单向振动速度为0.338 cm/s,均小于规程中最大单向振动速度0.5 cm/s,满足要求。

图9给出了调整炸药药量后1—3号摩崖石刻文物的位移响应时程曲线。由图9可知,同样的,1号石刻文物与2号石刻文物在X方向的位移响应时程曲线基本吻合,1号文物在三个方向的位移峰值明显大于其他两个石刻文物;且三处文物在X方向的位移与衰减程度均大于Y向与Z向,但X方向的持续时间却小于其他两个方向;在X方向产生最大瞬时位移仅为0.045 mm,在Y方向产生的最大瞬时位移约0.010 mm,在Z方向产生最大瞬时位移约0.015mm,且都随时间迅速衰减至接近0,表明这类位移不会对文物造成明显损伤。

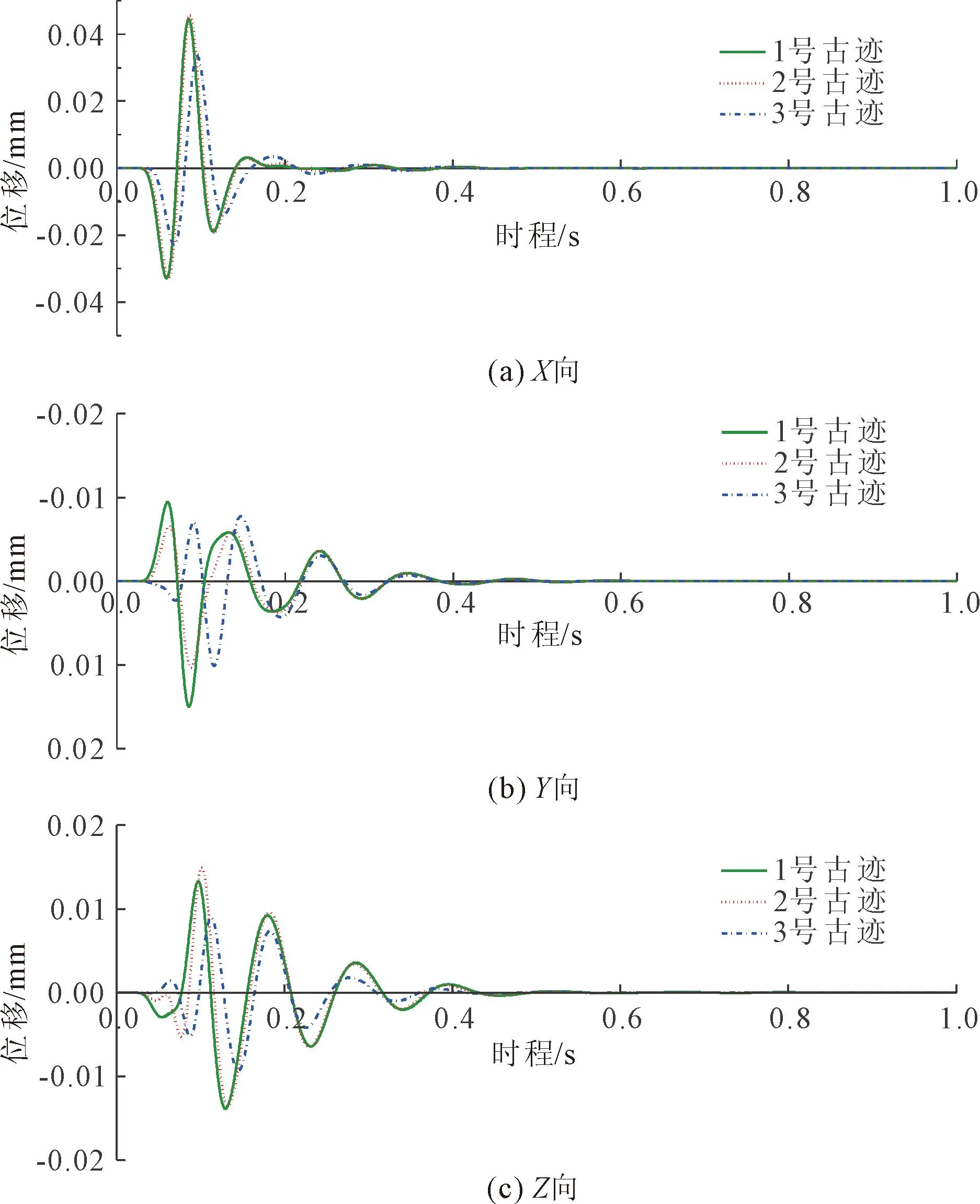
图9 调整药量后的石刻文物位移响应时程曲线

3.2.2 FDHK2+260—FDHK2+300典型爆破点2

FDHK2+260—FDHK2+300段隧道爆破施工的计算点为爆破点2,最不利爆破点位于FDHK2+300。参照表3可知,其最大单段药量为1.687 kg,相应的等效爆破荷载为30.918 MPa。

基于前述数值模型,图10给出了典型爆破点2在等效爆破荷载30.918 MPa作用下1—3号摩崖石刻文物的响应速度时程曲线。显然,由图10可知,1号石刻文物的最大单向振动速度仅为0.162 cm/s,2号石刻文物的最大单向振动速度约为0.172 cm/s,3号文物的最大单向振动速度为0.115 cm/s,均远小于《爆破安全规程》(GB 6722—2014)要求的最大单向振动速度0.5 cm/s,表明该段爆破施工所用的炸药量满足要求。

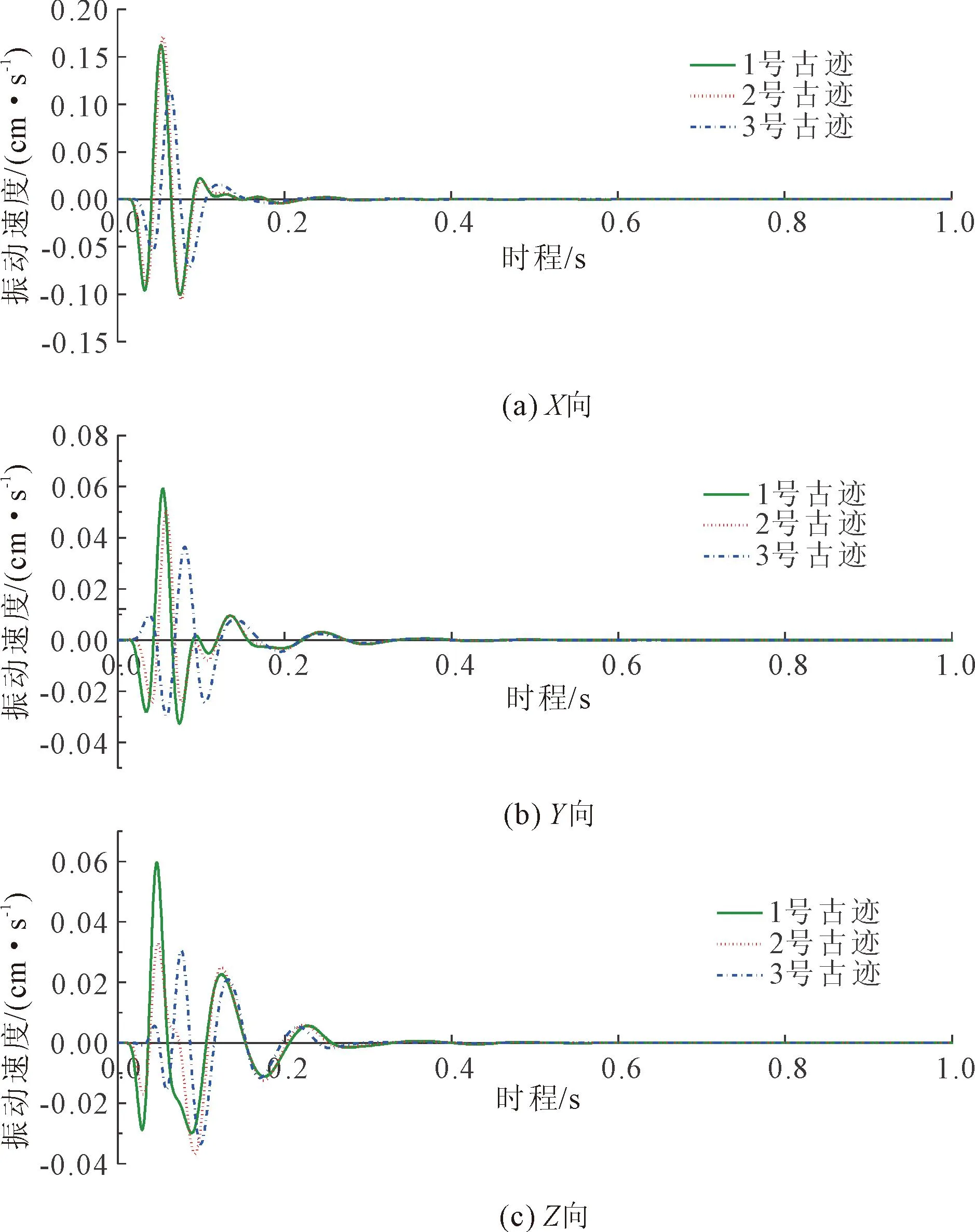
图10 典型爆破点2-不同石刻文物的速度响应

图11给出了爆炸荷载作用在典型爆破点2时1—3号摩崖石刻文物的位移响应时程曲线。

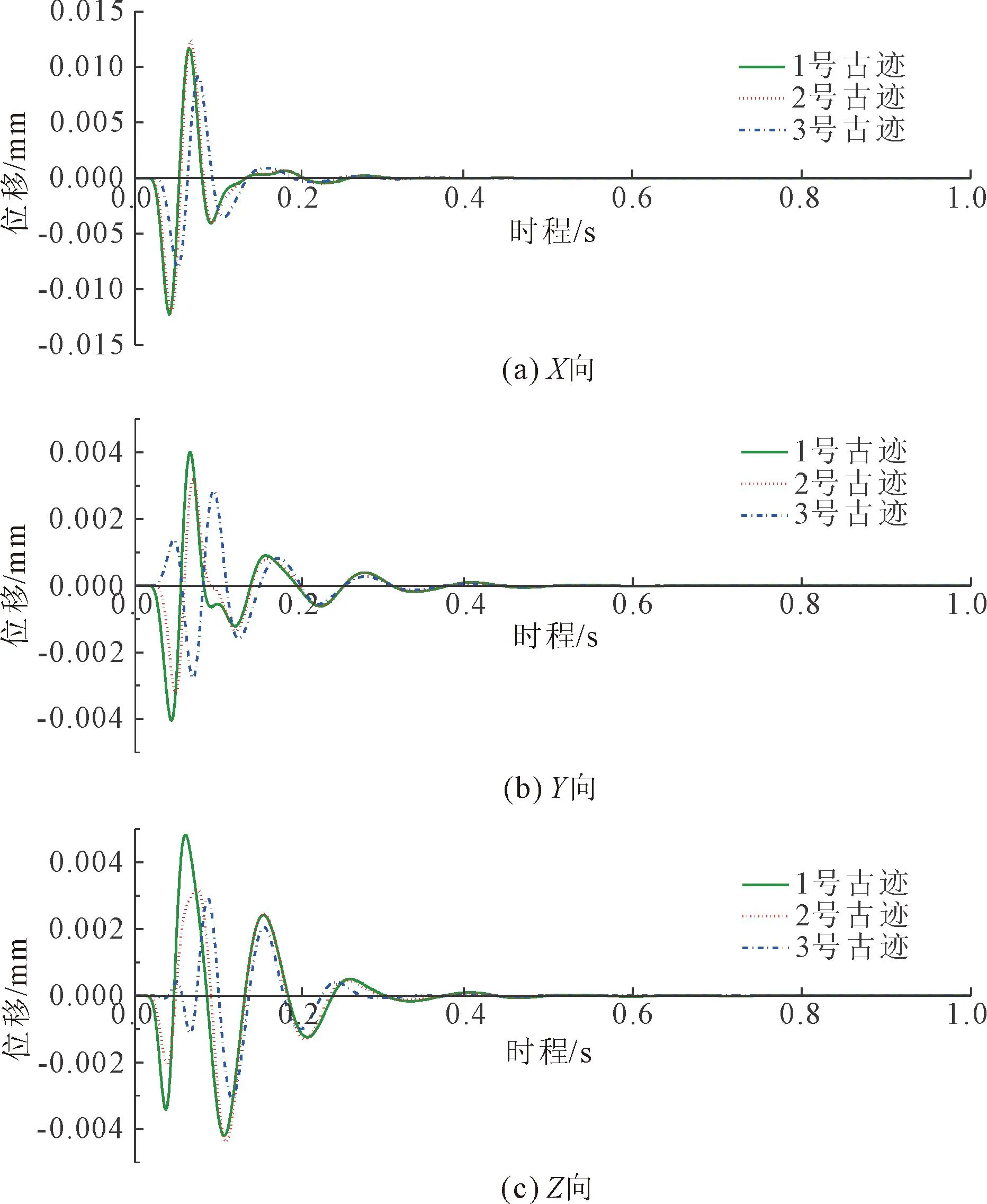
图11 典型爆破点2-不同石刻文物的位移响应

由图11可知,在该爆炸荷载作用下,三处石刻文物的最大瞬时位移约0.0125 mm,并随时间迅速衰减至接近0,说明该处隧道的爆破施工方案安全可行,对石刻文物的影响总体较小。

4 结 论

(1) 基于拟建隧道与既有石刻文物的空间位置与结构特征,采用有限元方法建立了隧道爆破振动作用下石刻文物的三维动力数值模型,并依托现有规程采用以质点单向振动速度作为石刻文物的安全评估标准,实现了对拟采用爆破方案的安全评估与改进。

(2) 针对两个典型爆破点开展了三维有限元动力时程分析,计算结果表明:FDHK2+220—FDHK2+260段隧道爆破施工时的最大单段药量为4.611 kg时,3处石刻文物的最大单向振动速度均小于0.5 cm/s;FDHK2+260—FDHK2+300段隧道爆破施工时的最大单段药量为1.687 kg时,3处石刻文物的最大单向振动速度也均小于0.5 cm/s。