Coverage in Cooperative LEO Satellite Networks

Bodong Shang,Xiangyu Li,Caiguo Li,Zhuhang Li

Abstract—Low-earth orbit (LEO) satellite networks ignite global wireless connectivity.However,signal outages and co-channel interference limit the coverage in traditional LEO satellite networks where a user is served by a single satellite.This paper explores the possibility of satellite cooperation in the downlink transmissions.Using tools from stochastic geometry,we model and analyze the downlink coverage of a typical user with satellite cooperation under Nakagami fading channels.Moreover,we derive the joint distance distribution of cooperative LEO satellites to the typical user.Our model incorporates fading channels,cooperation among several satellites,satellites’ density and altitude,and co-channel interference.Extensive Monte Carlo simulations are performed to validate analytical results.Simulation and numerical results suggest that coverage with LEO satellites cooperation considerably exceeds coverage without cooperation.Moreover,there are optimal satellite density and satellite altitude that maximize the coverage probability,which gives valuable network design insights.

Keywords—Low-earth orbit satellite,cooperative communications,coverage probability,satellite-terrestrial networks,non-terrestrial networks

I.INTRODUCTION

One of the fundamental goals for sixth generation (6G)networks is a radical increase in global coverage[1].Lowearth orbit (LEO) satellites,which establish a constellation,are expected to be densely deployed.Such non-terrestrial network (NTN) technology makes a paradigm shift in wireless connectivity where users on the earth’s surface could directly access the Internet through LEO satellites[2-4].

NTN has attracted a lot of attention in academia and industry.In the Release 14 stage,3rd Generation Partnership Project (3GPP) proposes satellite communication requirements and application prospects as a fifth generation(5G) access method.Technical discussions on NTN were held in Release 15[5]and Release 16[6],and standard protocol modifications began in Release 17[7-8].The development of global LEO satellites continues to be hot,and many parties have participated in the wave of satellite networking,including SpaceX Starlink,Amazon Kuiper,OneWeb,Telesat,and other companies that have successively planned satellite launch plans for various applications in NTN.

Satellite systems have been studied in the past.In Ref.[9],the authors investigated downlink coverage and rate in the LEO satellite constellation based on the binomial point process (BPP).However,the Rayleigh fading channels were assumed in satellite-terrestrial links,which are not applicable in practical systems but tractable in analysis.In Ref.[10],a Poisson point process (PPP) model was introduced to analyze the coverage of the LEO satellite networks.However,the authors did not consider satellite cooperation by assuming that users on the earth have access to their nearest satellite,which facilitates the Laplace transform in coverage analysis.In Ref.[11],cooperation between satellite and aerial relaying links was considered,where a satellite and an unmanned aerial vehicle(UAV)assist a group of other UAVs to forward their data to a remote destination.However,Ref.[11]only considered a single satellite,and the interference from other satellites was not incorporated.Such a single satellite model was also used in Ref.[12],where the authors derived outage probability/coverage probability and symbol error rate over satellite communication downlink channels when the users are randomly located in single beam and multibeam areas.In Ref.[13],the authors analyzed the satellite-to-airplane communication in the Terahertz band by assuming that the airplane connects to its nearest satellite.It is worth noting that the above works did not model and analyze cooperative LEO satellites in downlink joint transmissions.

In the research conducted by the author in Ref.[14],a comprehensive exploration was undertaken in the context of a LEO downlink satellite-terrestrial millimeter wave(mmWave)decode-and-forward relay network.The study’s conceptual framework assumed a PPP distribution for the terrestrial relay positions.The investigator utilized a sophisticated metadistribution methodology to meticulously extract and analyze the coverage performance of the network.In the work presented in Ref.[15],the authors examined a complex network configuration involving a single satellite,multiple terrestrial users,and an aerial relay.The spatial arrangement of these terrestrial users was represented using a homogeneous Poisson point process (HSPPP).Utilizing the shadowed-Rician (SR)fading model,the investigation systematically derived coverage and outage probabilities for both the satellite and terrestrial components.Furthermore,the study extended its focus to optimizing the end-to-end energy efficiency.Ref.[16]investigated downlink communication systems in LEO satellites,wherein multiple satellites are uniformly distributed across a sphere at a specific altitude,following a homogeneous BPP.The authors analytically derived the precise outage probability,and its approximate expression was derived through the application of the Poisson limit theorem.The optimization problem for system throughput was addressed using a proposed iterative algorithm,resulting in near-optimal solutions.Despite existing research effort[15]has addressed collaboration between satellites and aerial platforms to optimize signal transmission efficiency,a notable gap persists in the literature concerning inter-satellite cooperation.Consequently,our study endeavors to bridge this research gap by systematically investigating and addressing this intricate facet.

Satellite cooperation is one of the ways to increase coverage by enhancing the desired signal strength and reducing co-channel interference.The densification of LEO satellites facilitates satellite cooperation,especially for a user in remote areas with many visible satellites.In situations marked by extraordinary conditions,especially in remote regions characterized by a sparse user population but abundant satellite availability,the imperative to optimize the efficient utilization of satellite communication resources becomes evident.In pursuit of this objective,this paper introduces an innovative model that harnesses multiple satellites for transmitting identical data while employing a single-user signal reception methodology,as shown in Fig.1.Simultaneously,it is noteworthy that typical users contend with interference from interfering satellites.Consequently,we comprehensively analyze the coverage probability within the model mentioned above.The contributions of this paper are summarized as follows.

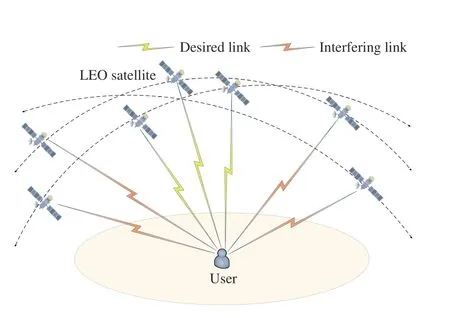
Fig.1 An illustration of cooperative LEO satellite networks

• Cooperative LEO satellites modeling:We introduce a satellite cooperation system where several nearest satellites jointly transmit data to the typical user.Moreover,we consider the large-scale distance-dependent path-loss and smallscale Nakagami-mfading in each serving and interfering link.

• Coverage probability analysis:We derive the coverage probability under Nakagami-mfading channels by analyzing the Laplace transform of interference and the desired signal distribution.An approximated but tractable expression of coverage probability is derived.Furthermore,the joint distance distribution of the serving satellite and the expectation of interference power are given.In addition,the coverage of two and three cooperative satellites are given,respectively.

• Network design insights:Simulation results demonstrate that coverage probability with satellite cooperation is significantly improved compared to that without satellite cooperation.Specifically,coverage can be enhanced by more than 100 percent when only two satellites work cooperatively.Moreover,there is an optimal combination of satellite altitude and the number of satellites in cooperative LEO satellite networks that maximize the coverage probability.

The paper is organized as follows.Section II presents the system model including network model,channel model,and signal model.Section III develops intermediate results that will be used in coverage derivations.Section IV derives coverage probability for a typical user in cooperative LEO satellite networks.Simulation and numerical results are discussed in section V.Section VI concludes the paper.

II.SYSTEM MODEL

In this section,we introduce system model in cooperative LEO satellite networks.In this system,we consider the LEO satellites are coordinated via a central base station which is deployed either on the ground or on one of LEO/MEO satellites with more advanced computing capabilities and sufficient power.The locations of the central base station can be known.When the typical user confirms several nearest LEO satellites for service,it will initiate a connection request to the central base station.The central base station will then coordinate these serving LEO satellites to simultaneously transmit signals to the typical user.Similar cooperative modes of LEO satellites can be referred to Refs.[17-18].

A.Network Model

In our analysis,we begin with the foundational assumption that both serving and interfering satellites are positioned on the surface of a sphere,characterized by a radius denoted asRS,shown in Fig.2.The spatial distribution of serving satellites is rigorously modeled using a homogeneous spatial Poisson point process(SPPP),wherein the density parameter governs the distribution.Consequently,the setΦS={X1,···,X2}represents the discrete locations of serving satellites.Here,each fori ∈Nis considered as an independent and uniformly distributed point on the surface of the sphere.The variable signifies the number of serving satellites allocated to the typical userk,following a Poisson distribution.As a result,|ΦS|=N.Similarly,the quantity|ΦI|denotes the number of interfering satellites that affect the typical userk.This parameter also adheres to a Poisson distribution.Each satellite in the system operates with a transmit power represented asPT,while the satellite transmit antenna gain is denoted byGT.Additionally,it is essential to consider the geographical placement of a typical user on the earth’s surface,which is characterized by a radiusRE.Our model assumes that wireless transmissions to the user exclusively originate from satellites positioned above its local horizon.

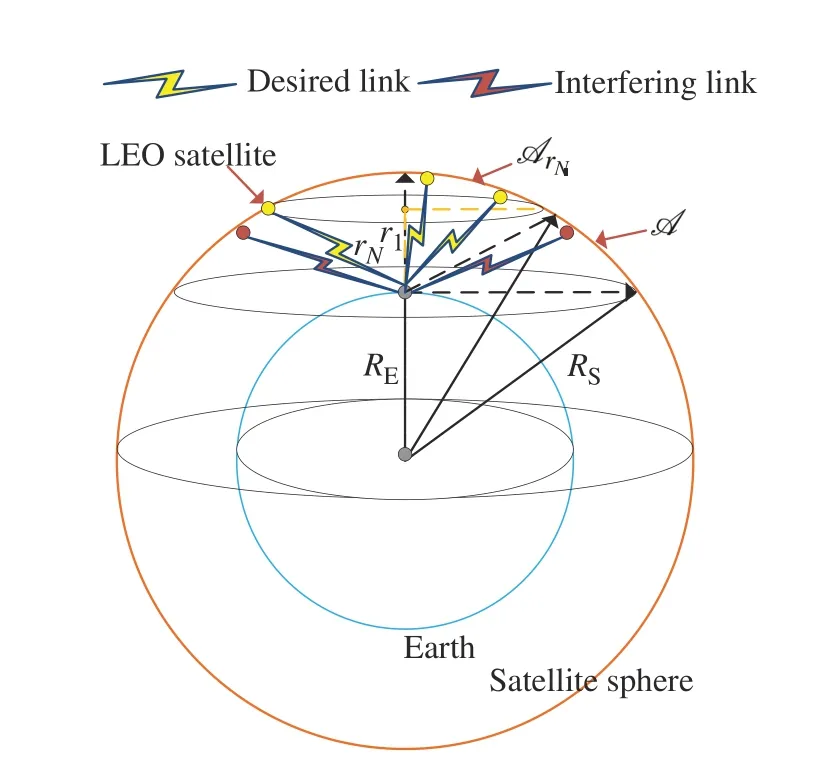
Fig.2 Geometry of cooperative LEO satellites

We consider a typical user positioned at coordinates(0,0,RE).As illustrated in Fig.2,we define a typical spherical capAthat lies within the field of view at the location of the typical user.For clarity,this spherical cap signifies the section of the surface of the sphere with radiusRSthat intersects with a tangent plane to the earth.The center of this tangent plane is located at coordinates(0,0,RE).The surface area of this typical spherical cap can be written as

Moreover,we define a spherical capAriwith a distancerifrom the typical receiver’s location.This cap encompasses all points located within a distance less thanrifrom the typical receiver’s position,the surface area ofArican be written as

We note that only the satellites on the typical spherical capAare visible to the typical user.

B.Channel Model

The wireless channel propagation is characterized by a composite model encompassing path-loss attenuation and small-scale fading.We employ the free-space path-loss model to account for large-scale fading effects,defined as

In this equation,β0represents the path loss at a reference distance,risignifies the distance between theith nearest satellite and the typical user,andαdenotes the path loss exponent.We adopt the Nakagami-mdistribution to introduce the element of randomness associated with small-scale channel fading.Lethidenote the fading coefficient betweenith nearest satellite and the typical user.We modelhiashi～Nakagami(m,Ω),where|hi|2～Gamma(k,θ),withk=m,θ=Ω/m.Under the assumption ofE[|hi|2]=1,the probability density function(PDF)ofhitakes the following form

where Γ(m)represents the gamma function defined as Γ(m)=.The Nakagami-mdistribution offers versatility in modeling a wide range of small-scale fading phenomena.Notably,it converges to the Rayleigh distribution form=1 and to the Rician-Kdistributions form=(K+1)2/(2K+1).For Shadowed-Rician(SR)fading in satellite-terrestrial communications,the SR fading can be approximated by a Nakagami distribution with appropriate shape and scale parameters.The general expression for channel coefficients linking satellites and the typical user can be succinctly written as

C.Signal Model and SINR

We consider that a typical user is being served byNnearest satellites while simultaneously experiencing interference fromΦIsatellites.Accordingly,the received signal at the typical user located at(0,0,RE)is expressed as follows.

Letxrepresent the transmitted signal originating from the serving satellites to the typical user.The simultaneous transmission of identical signals to the typical user by multiple collaborative satellites designates transmitting satellites as‘serving satellites’.However,owing to the LEO satellite mega constellation and LEO satellites near random distribution given a time slot,within the observable region of the typical user,numerous satellites concomitantly use the same channel for signal transmission to other users,termed‘interfering satellites’,these entities contribute to the aggregated interference signal power received by the typical user,so it is imperative to undertake an analysis of co-channel interference for the typical user.LetIdenote the interfering signal emanating from interfering satellites to the typical user.The power of the interfering signal at the typical user is designated as

whererI,isignifies the distance between theith interfering satellite and the typical user,andhI,irepresents the small-scale fading coefficient between theith interfering satellite and the typical user.

The signal-to-interference-plus-noise ratio (SINR) at the typical user equipped with a single antenna is

wheredenotes the variance of the noise.It is worth noting that the ground user’s location and satellite ephemeris are known,and thus the timing advance can be compensated in cooperative transmission from multiple satellites.In addition,the robust downlink synchronization performance can be provided by the synchronization signal block (SSB) design in NTN[5-6].

D.Coverage Probability

The performance metric,in this paper,known as coverage probability,is formally defined as follows

whereγthrepresents the minimum SINR required for successful data transmission.In simpler terms,when the SINR of the typical user,considering both itsNserving satellites and|ΦI|interfering satellites,exceeds the threshold valueγth,it is considered to be within the coverage area of the satellite communication network.

III.INTERMEDIATE RESULTS

In this section,we derive some intermediate technical results that will be used in the calculation of coverage probability in the sequel.

Lemma 1The joint distance distribution ofNnearest serving LEO satellites is shown as follows.

ProofWe first derive the distribution of the two nearest satellites,then derive the distribution of theNclosest satellites.The distribution of the closest satellites is given by

The joint distance distribution of two nearest satellites to the typical user is expressed as

whereA/Brepresents the area thatAexcludesB.The cumulative distribution function (CDF) ofr2conditioned onr1is given by

and we have

Then,the probability density function (PDF) ofr2conditioned onr1is obtained by calculating the derivation of its CDF,as follows.

Finally,the joint distribution ofr1andr2is obtained as follows.

Based on the above result,we can generalize to any numberNof cooperating LEO satellites.The joint distance distribution ofNnearest LEO satellites is

which completes the proof.

When the LEO satellites are densely deployed,the typical user has a high probability to observe its serving satellites.Therefore,we have a simplified expression of the joint distance distribution ofNnearest LEO satellites,as shown in Lemma 2.

Lemma 2In dense LEO satellite networks,the joint distance distribution ofNnearest serving LEO satellites is approximated by

ProofWhen the LEO satellites become dense,the denominator in Lemma 1 approaches to one,and thus we have

Lemma 2 is obtained from(20)with some mathematical manipulations.

IV.COVERAGE PROBABILITY

Now we are in the position of deriving coverage probability of cooperative LEO satellite networks.

A.Main Results

The coverage probability of a typical user is derived in the following.

Theorem 1The coverage probability for the typical user in a downlink cooperative LEO satellite network whereNLEO satellites jointly transmit to it is given in(23)at the top of the next page.

ProofThe coverage probability can be reformulated as

Then,we derive the Laplace transform of the summation of small-scale fading channel power gain,the Laplace transform of interference and noise power.

By utilizing the Laplace transform,the coverage probability is given in(25).

In the following,we derive the Laplace transform of the interference power in(26).

By substituting(26)to(25),we obtain the desired results,which completes the proof.

In Theorem 1,we give an analytical expression of coverage probability for the typical user based on Laplace transform.However,Theorem 1 involves multiple integrals which reduces the analytical tractability.In the following Theorem,we give an approximated coverage probability based on the fading distribution which is simple and concise.

Theorem 2An approximated coverage probability for the typical user in a downlink cooperative LEO satellite network whereNLEO satellites jointly transmit to it is given by

ProofThe coverage probability for a typical user is derived in (29).In the first step of (29),we use the upper bound of the desired signal power under Nakagami-mfading channel,

where,in(a),we use the incomplete Gamma function to represent the distribution of the sum of small-scale channel power gain,in (b),we use the joint distance distribution function which is obtained in Lemma 1 and Lemma 2 to average the distance between serving satellites and the typical user,in(c),we calculate the average interference directly to achieve an approximated coverage probability.

Note that the average interference power at the typical user is obtained by using Campell theorem and averaging onrN,which is shown as follows.

where(rN) is given in which is obtained from the joint distance distribution.

After some mathematical manipulations,we obtain the desired results in(27),which completes the proof.

B.Particular Cases

In this subsection,we derive some valid but closed-form technical results in particular cases.These results help identify the fundamental coverage improvement when LEO satellites collaborate in transmissions compared to the traditional LEO satellite network without cooperation.We provide the closed-form results with two and three satellites involving cooperation in the following,respectively.

Corollary 1WhenN=2,the coverage probability for the typical user in a downlink cooperative LEO satellite network where two LEO satellites jointly transmit to it is expressed as follows.

ProofBased on the intermediate results derived in section III,we can obtain the joint distance distribution of cooperative LEO satellites to the typical user.WhenN=2,the joint distance distribution is given by

Thus,the PDF ofr2is derived as follows.

By substituting the PDF ofr2to the expression of average interference power,we obtain the closed-form interference power forN=2,shown in (34) at the top of the next page.It is worth noting that the average interference power incorporating lower incomplete Gamma functions can be calculated efficiently.

Substituting (33) and (34) into (29),we can express (31),which completes the proof.

Corollary 2WhenN=3,the coverage probability for the typical user in a downlink cooperative LEO satellite network where three LEO satellites jointly transmit data to the user is expressed as

ProofBased on the joint distance distribution of cooperative LEO satellites to the typical user which was derived in section III,we obtain a concise form of this distribution.Specifically,whenN=3,the joint distance distribution in satellite cooperation is given by

Thus,the PDF ofr3is derived as follows.

The average interference power at the typical user is

Substituting (37) and (38) into (29),we can express (35),which completes the proof.

We have completed the main results of this paper,i.e.,the derivation of coverage probability for a typical user with LEO satellites cooperation under Nakagami-mfading channels.By setting differentmvalues such asm=1 andm=∞in the expressions,we can obtain the coverage probabilities for Rayleigh and no-fading cases,respectively.

V.SIMULATION AND NUMERICAL RESULTS

In this section,we numerically evaluate and validate the coverage probability against important parameters for the typical user in cooperative LEO satellites,including altitude,Nakagami fading parameterm,number of cooperative satellites and total number of satellites.In addition,we also illuminate a trade-off between the desired signal power and the interference signal power under the impacts of the number of satellites and the altitude of satellites.

We do Monte Carlo simulations in MATLAB for the comparison of the simulation and analysis results.As is shown in Fig.3,we first depict a 3D diagram for LEO satellite networks.The users and LEO satellites are respectively distributed on the earth surface sphere and satellite orbit sphere independently,according to homogeneous SPPP with different densities.

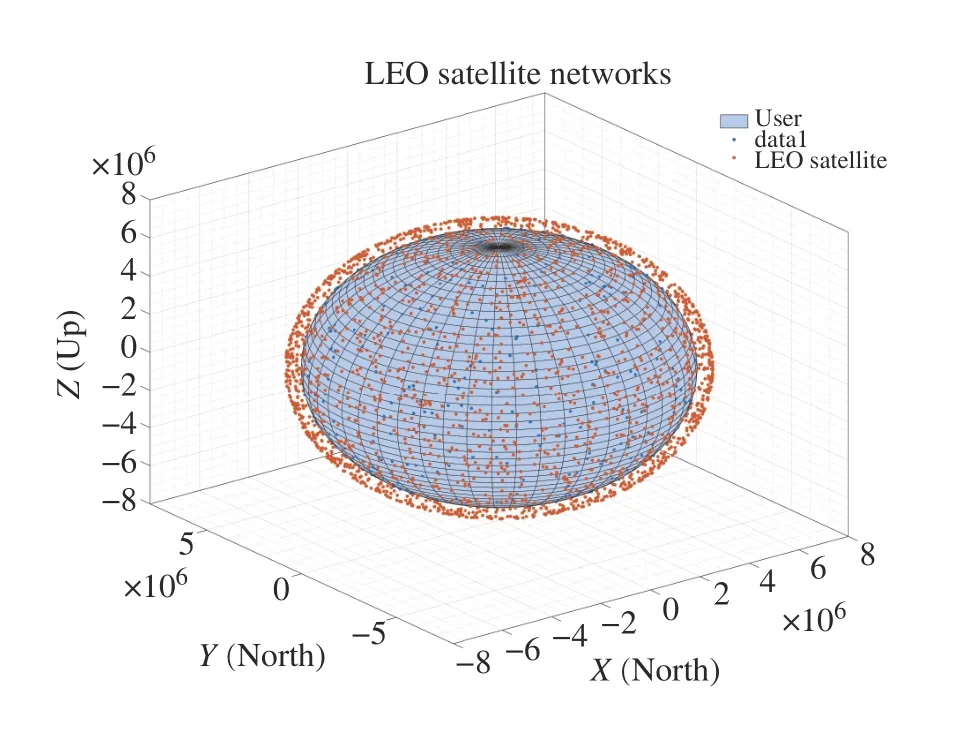
Fig.3 An illustration of simulation scenario

In simulations,we setRE=6 372 km,the path loss exponentα=2.1,the density of LEO satellitesλS=(1e-12)/m2,the Nakagami fading parametersΩ=1,m=2,transmit power at the LEO satellitePT=1 Watt,transmit antenna gainGT=30 dBi,unless specified otherwise.

Taking into account the impact of the serving satellite number,Fig.4 shows the coverage probability under different numbers of serving satellites,compared with traditional nocooperation scenario.It is found that with the increase of serving satellite number,the coverage probability of cooperate LEO satellite networks becomes higher under the given SINR threshold.

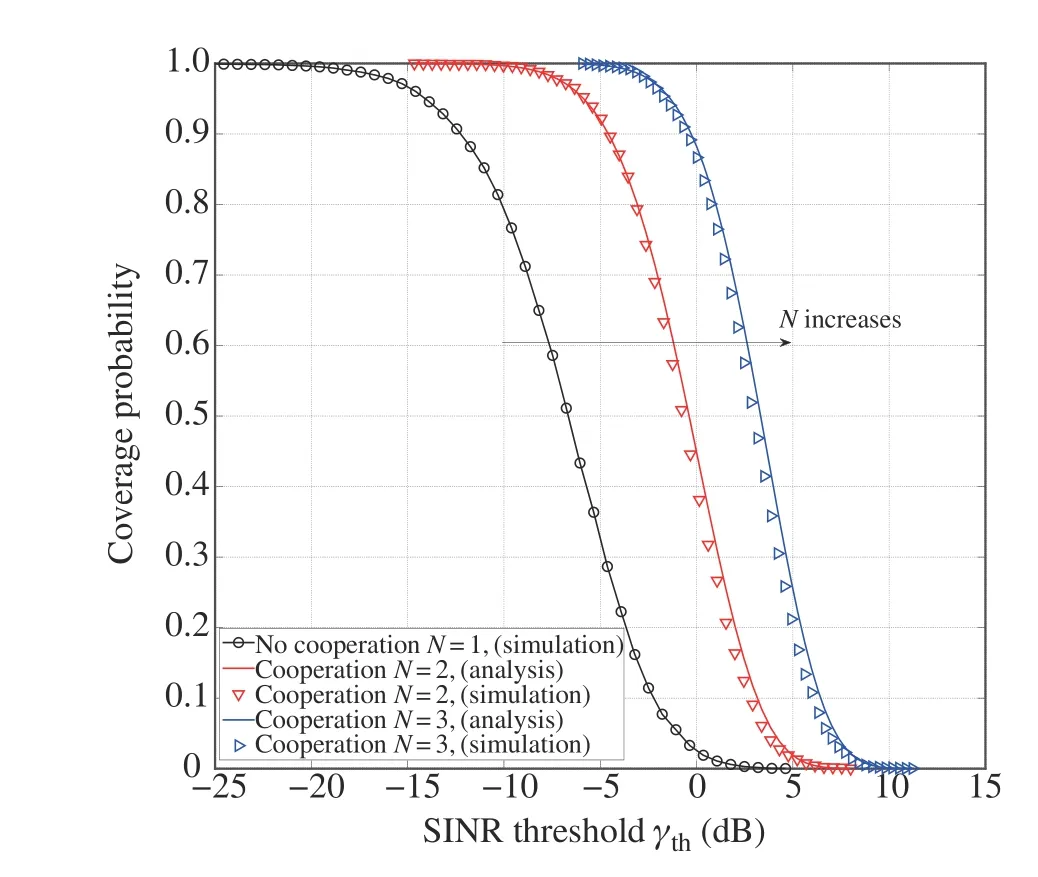
Fig.4 Coverage probability versus the SINR threshold under different numbers of serving satellites,where m=2

Fig.5 compares the coverage probability under different Nakagami fading parameter m.It is clear that the case ofm=4 outperforms other cooperation counterparts when the SINR threshold is lower than 1 dB;however,its coverage probability drops fastest as SINR threshold increases,thus it is surpassed by that of other cases.Note that no-operation case falls far behind the cooperation cases.

Fig.5 Coverage probability versus the SINR threshold under different Nakagami fading parameters m

The impact of satellite altitudes on the coverage probability of cooperative LEO satellite networks is compared in Fig.6.It is revealed that for both cooperative and non-cooperative scenarios,the coverage probability increases with the altitude;however,for the same altitude,the cooperative case enjoy apparently higher coverage probability than it opposite noncooperative case.This is because with a lower altitude,the increase of desired signal power dominates the increase of interference power,resulting in the improvement of SINR and coverage probability.

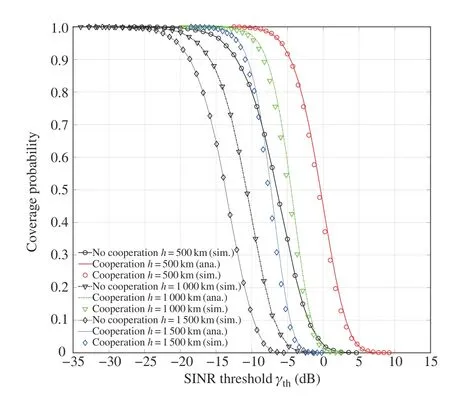
Fig.6 Coverage probability versus the SINR threshold under different altitudes of satellites,where N=2,m=2

In the case of serving satellite quantity isN=2,Nakagami fading parameter ism=2,and the SINR threshold being-3 dB,we conducted a comparative analysis of coverage probability concerning satellite altitude across varying satellite quantities,both with and without satellite cooperation.This analysis aimed to substantiate that the implementation of LEO satellite cooperation significantly enhances downlink coverage,surpassing the coverage achievable in the absence of cooperation.

Fig.7 provides a comparative assessment,elucidating the coverage probability in situations involving satellite cooperation (indicated by colored lines) versus non-cooperation(depicted by black lines) with respect to satellite quantities of 500 (represented by lines with circles) and 1 000 (indicated by lines with triangles).The visual evidence gleaned from the figure unequivocally highlights that the collaborative transmission of data among serving satellites leads to a substantial enhancement in coverage probability for ground user,as opposed to scenarios where such cooperation is lacking.This performance improvement is conspicuously discernible within the graphical representation.

Fig.7 Coverage probability versus the altitude of satellites with different SINR thresholds,where N=2,m=2,γth=-3 dB

Furthermore,upon examining the scenario of noncooperation among satellites in Fig.7,denoted by the black line with circles as opposed to the black line with triangles,we can deduce that a smaller satellite number exhibits a higher coverage probability.This observation also holds true in the context of cooperation among serving satellites.This is because the network with a smaller satellite number has a lower co-channel interference power than the network with a high satellite number,and thus it is beneficial to the coverage.

Moreover,in instances where satellites do not engage in cooperative behavior,there is a noticeable decline in coverage probability with increasing satellite altitude.Upon closer examination of the blue and red lines depicted in Fig.7,it becomes evident that even when satellites cooperate,the coverage probability experiences a decline as satellite altitude rises.However,it is noteworthy that slight increments are observed when satellite altitude remains below 150 km.This is because that when the satellite altitude is very low,the typical user could not always see the sufficient serving satellites for cooperation.When the satellite altitude is very high,the desired signal power decreases due to the increased distancedependent large-scale fading.Therefore,there is an optimal satellite altitude given the number of satellite.

Next,we investigate the relationship between the number of satellites and the coverage probability under fixed satellite altitudes.When the number of satellites increase from 60 to 6 000 as is shown in Fig.8,a decreasing trend is witnessed for each of the four cases,with and without cooperation.Similarly,a tiny increase can be seen in coverage with a low altitude under cooperation mode.On the contrary,the no-cooperation satellite system experiences a continuous and sharp decrease in coverage from approximately 0.7 and 0.8 to 0 as the number of satellites come to nearly 4 000.There is also an apparent performance gain between cooperation and no-cooperation cases.

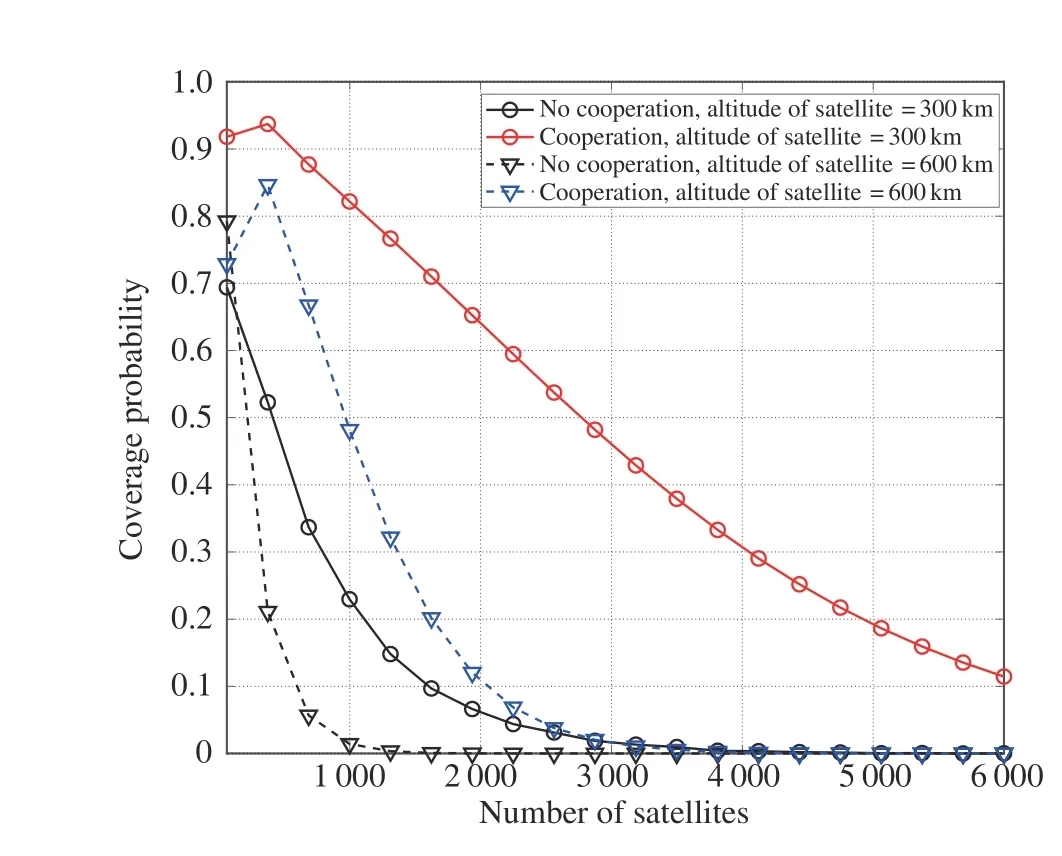
Fig.8 Coverage probability versus the altitude of satellites with different SINR thresholds,where N=2,m=2,γth=-3 dB

In Fig.9 and Fig.10,we examine the coverage probability versus the number of satellites and the altitude of satellites in 2D and 3D views,respectively.We observe that there is an optimal combination of the number of satellites and satellite altitude,which gives system design insights.The reasons behind this are as follows.Regarding satellite altitude,there is a trade-off between the probability of seeing sufficient serving satellites in cooperation and the desired signal power at the typical user.Regarding the number of satellites,there is a trade-off between the distance-dependent path loss (or the desired signal power) and the interference power from other satellites.Moreover,we observe from Fig.9 and Fig.10 that when deploying dense LEO satellites for satellite-terrestrial communications,it is better to reduce the satellite altitude.This is because for densification of satellites,reducing satellite altitude deceases the number of interfering satellites for the typical user and increases the desired signal power.This guided us to seize the low-earth orbit.

Fig.9 Coverage probability versus the altitude of satellites and the number of satellites,where,where N=2,m=2,γth=-5 dB

Fig.10 Coverage probability versus the altitude of satellites and the number of satellites in a 3D plot,where N=2,m=2,γth=-5 dB

VI.CONCLUSION

In this paper,we proposed and modelled a novel satellite cooperation system which incorporates several nearest satellites to provide services to the typical user.Considering the satellite altitude,Nakagami fading channels,the number of serving satellites and all visible satellites,and other related parameters,we derived approximated but tractable and closedform expressions for the coverage probability of the satellite cooperation system.It was shown that in the satellite cooperation system,the increase of cooperative satellite number significantly brought about larger coverage for the typical user,significantly surpassing that in non-cooperative satellite downlink transmission system.Specifically,there is a tradeoff between the desired signal power and the interference signal power brought by the total number and the altitude of satellites.