基于结构方程模型的心理问题预测算法设计

刘晓媛

（西安航空职业技术学院，陕西西安 710089）

大学生由于社会经验不足，且抵抗外部干扰的能力有限，有时会受到社会及周围环境不良风气的影响，导致其自身心情焦虑、不安甚至抑郁[1]。面对学业、就业、生活与感情等方面的压力，大学生在情绪上通常会出现不同程度的波动。这些波动若不加以重视，有可能会造成一定的心理问题，从而导致一些负面事件的出现[2-4]。为此，亟需一种心理健康预警算法来对大学生的心理状态进行有效分析。且在出现异常情况时，能够及时预警并加以处理。

针对上述问题，文中基于结构方程模型（Structural Equation Modeling，SEM）提出了一种心理问题预测算法。该算法通过分析心理问题中潜变量与观测变量的关系建立模型，从而实现对心理问题的预警。该算法的提出有助于精准地确定预警对象并及时发现其心理数据中隐藏的危机因素，进而为高校健康的学习、生活氛围提供重要保障。

1 结构方程模型的建立

结构方程模型又被称为协方差结构模型，其是一种运用线性方程建立、预测及检验模型影响因子的统计算法[5]，该模型还是一种既考虑不同影响因子间的联系又考虑因子内部结构的多变量分析模型。此外，SEM 模型中包含了两个重要的名词：潜变量和观测变量。

潜变量[6]是指包含隐藏知识，但又无法被直接测量，并需根据已测量结果间接计算或分析而来的变量，也可称为隐藏变量。这类变量通常是系统或模型所要深入分析、研究的重点。且根据影响作用域的不同，该变量可细分为内生潜变量与外生潜变量两种。其中，内生潜变量是指在模型中易受其他变量影响、并在路径图中表现为有入向箭头的潜变量；而外生潜变量则代表在影响其他变量的同时，自身并未受到影响的潜变量，且其在路径图中的表现为只有出向箭头而没有入向箭头。

观测变量[7]的概念与潜变量相对，具体是指能被直接观察及测量的变量，这类变量通常可利用调查问卷等统计方法得到。同时，其是获得潜变量并分析潜变量与观测变量、潜变量与潜变量之间隐藏关系的必要条件。除了上述提到的潜变量与观测变量外，结构方程模型中还包括一些其他的名词，例如中介变量、残差项、自由参数、固定参数及限定参数等。该模型的结构如图1 所示[8]，其主要包括测量和结构模型两部分[9-10]。

图1 结构方程模型拓扑

其中，测量模型负责对观测变量与潜变量间的关系进行描述。由于潜变量也被视作因子，所以该模型有时也被称为因子分析模型，而模型中的方程则被称为测量方程[11]。结构模型负责对潜变量与潜变量之间的因果关系进行描述，故也可称之为因果模型，而其所包含的方程则称作结构方程。

1）测量模型

测量模型可用以下两个线性方程来描述，其中式（1）描述外生潜变量与外生观测变量间的关系，而式（2）则用来描述内生潜变量与内生观测变量间的关系。具体方程为：

式中，x、y分别代表内、外生观测变量；Λx和Λy表示与内、外生观测变量相对应的潜变量之间的函数关系，即因子载荷矩阵；ξ及η代表与内、外生观测变量相对应的潜变量；σ和ε代表内、外观测变量与对应潜变量在相互转换过程中所应考虑的误差。

2）结构模型

结构模型反映了潜变量之间的相互关系，对应的结构方程为：

式中，B代表内生潜变量之间的关系；T表征外生潜变量对内生潜变量的影响；ζ表征结构方程的误差项。

SEM 的建模过程通常可分为模型准备与评价两个步骤，而这两个步骤又可细分为多个小步骤，具体如图2 所示。

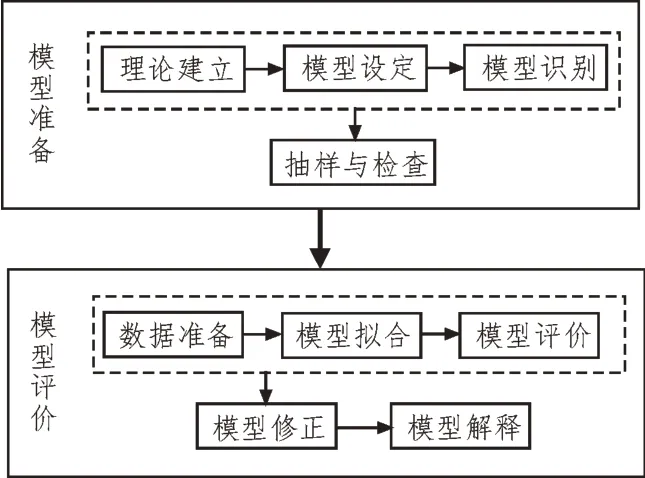
图2 SEM建模过程

在SEM 建模过程中，理论建立根据用户的需求确定建模所需的基本流程及搜集必要的资料。模型设定负责将文字等资料转换为SEM 语言，同时确定模型中所涉及的观测变量与潜变量；然后再根据模型结构将潜变量与观测变量之间的关系记为测量模型，将潜变量与潜变量之间的关系记为结构模型；最后，对模型中的自由和固定参数进行初始化设置。模型识别则负责对模型所设定的参数进行评价与进一步的优化，从而使模型在初始化时的拟合程度更高。该步骤的识别结果主要分为3 种：识别不足、恰好识别及过度识别。若没有该步骤，则可能导致在后续统计分析时模型无法进行拟合。抽样与检查主要是根据建立模型，采集符合条件的模型验证材料。而数据准备是数据验证的第一步，负责对采集的材料进行可信度及有效度的校验，进而使模型得到的结果更为准确。模型拟合则为SEM 建模的关键部分，其通过统计分析的方法建立与样本协方差矩阵最为接近的再生矩阵。同时利用最大似然估计法（Maximum Likelihood，ML）[12]对模型进行拟合，令卡方值在有限迭代次数中为最小。模型评价负责对得到的模型做进一步评定，常用的评价指标包括卡方值、规范拟合指数（Normed Fit Index，NFI）及近似误差均方根（Root Mean Square Error of Approximation，RMSEA）等。而模型修正根据模型评价结果对其参数进行修正与优化，进而使模型的拟合效果更优。模型解释则通过模型来获得所需结果以及变量间的关系。

2 预测算法设计

2.1 心理问题应激源问卷编制

编制该应激源问卷的目的在于，对影响大学生心理波动的主要因素进行归纳，从而确定各应激源所属维度及对应的各级指标。

该文根据各高校原有的心理健康调查问卷，确定了若干个题目，形成了符合要求的应激源问卷。采用随机抽样的方法，在高校各年级抽取了500 名学生作为被调查者进行问卷填写，并收回有效问卷共435 份。然后使用因子分析法（Factor Analysis Method，FAM）对结果进行分析，且根据所得结果对问卷题目进行调整，从而形成新的应激源调查问卷。随后利用随机抽样的方法再选择500 名学生进行问卷调查，并对此次回收的452 份有效问卷加以分析。同时根据美国伊贝尔学者测验的经验，去除了鉴别能力指数在0.4 以下的题目项，最终共保留了54 个题目。

2.2 因子分析

因子分析[13]的目的在于发现所编制问卷中潜在的结构，并进一步对问卷内容加以优化，包括题目删减与修改等。从而使问卷内容成为相关性较大的变量，且由此检验该问卷能否充分满足设计需求。根据因子分析的结果，KMO 检验系数（Kaiser-Meyer-Olkin-Measure of Sampling Adequacy）为0.91、Bartlent检验的卡方统计量为2 817.58，显著性水平为0，这些结果说明了所编制的问卷适合进行该类分析。因此利用上文得到的问卷进行第三次问卷调查，并采用四次方最大法求出因子载荷矩阵，再使用主成分分析法（Principal Component Analysis，PCA）抽取其中的5 个公因子。同时删除与公因子的鉴别指数在0.4 以下的问卷题目，并由剩下的45 个题目形成最终问卷。所对应的部分心理问题应激源问卷的因子载荷矩阵，如表1 所示。

表1 部分应激源问卷因子载荷矩阵

如表1 所示，该文确定的5 个公因子为学习压力、就业压力、社交压力、家庭压力及异性压力。

2.3 可信度和有效度校验

此次主要测试问卷的可信度与有效度，可信度代表了问卷的可靠程度，其能够反映出检验结果的一致性与稳定性；而有效度则代表了对测量问题所能达到的准确程度。

1）可信度校验

该文利用克朗巴哈系数（Cronbach’sα）作为检验问卷可信度的标准，其取值范围在[0,1]之间，且取值越大可信度越高。具体测量结果，如表2 所示。

表2 可信度校验结果

从表2 结果可以看出，5 个公因子的Cronbach’sα值均在0.82 以上，而总问卷则达到了0.933。因此其完全满足设计需求，说明该问卷具有良好的可信度。

2）有效度校验

该文利用相似性计算的方法校验问卷的有效度，但其相似性不能过高或过低。通常各因子间的相似性处于0.1～0.5 的范围内，而各因子与总体之间的相似性则处于0.4～0.8 之间为宜。该项校验结果，如表3 所示。

表3 有效度校验结果

由表3 结果可知，各因子间的相似性及各因子与总体之间的相似性均处于理想范围内，说明该问卷具有较优的有效性。

3 实验与分析

3.1 实验数据准备

1）研究对象

采用随机抽样的方法，在各年级分别发放问卷，且总共600 份问卷。回收了540 份有效问卷，其中三个年级分别为142 份、138 份及260 份问卷，有效回收率为90%。

2）数据分析

该文采用SPSS（Statistical Product Service Solutions）对问卷结果加以处理，并利用因子分析法对原始高维的问卷信息进行降维操作。同时通过LISREL（LInear Structural RELations）对SEM 模型进行分析，进而讨论应激源与心理危机之间的关系。

在利用因子分析法对原始信息做降维处理的过程中，首先得到KMO 检验系数为0.897。而Bartlent检验结果的P值则趋近于0，说明此时原始问卷中的变量适合进行因子分析。所以经过分析将公因子由原始的5 个重新组合为3 个，分别为自身压力（包括学习和社交两个维度）、外界压力（包括就业和家庭两个维度）及异性压力。

3.2 心理危机指标体系构建

根据学生心理问题的特点，建立了如表4 所示的相关心理危机指标体系[14-16]。该体系由2 个一级指标，5 个二级指标以及10 个三级指标所组成。

表4 学生心理危机指标体系

3.3 相关性分析

在建立SEM 模型前首先要保证各因子间的相关性，因此采用Person 分析法（Pearson Correlation Coefficient）对心理健康及应激源中的因子进行了分析。得到的结果，如表5 所示。

表5 因子相关性分析结果

由表5 可知，心理健康与应激源的3 种公因子存在明显的相关性。

3.4 SEM心理预警模型构建

所提SEM 心理预警模型以心理健康为内生潜变量，精神及生理压力为间接描述心理健康的观测变量，而应激源为外生潜变量，自身、外界及异性压力则作为外生潜变量的观测变量，并按照上文方法进行构建。利用LISREL 执行后对模型进行拟合校验，校验结果的常规指标如表6 所示。

表6 模型拟合校验结果

由表6 可知，模型的拟合效果较为理想。同时通过检验，该模型的各项系数均能达到显著性水平，故证明了所提算法的可行性。

4 结束语

该文分析了结构方程模型技术的基本原理、结构及建模过程，提出了一种基于结构方程模型的心理问题预测算法。通过发掘并分析心理问题中潜变量与观测变量之间的关系，实现对心理问题的预警。实验结果充分说明了应激源与心理健康之间的各种相关性，证实了所提方法的有效性。