基于改进A*算法的机器人路径规划与避障技术

黄宸希，韩韬，吴雪琼，冯荣强

（南瑞集团公司（国网电力科学研究院），江苏南京 211100）

随着信息技术的发展，巡检机器人作业被广泛应用于各个领域[1]，且目前已实现了根据巡检点位置进行自动巡检的功能。但对于复杂应用场景，其仍存在自主避障能力弱、运算消耗的内存资源较大等缺陷，从而制约了该技术的进一步发展。因此，针对巡检机器人精准巡检、智能避障及性能优化等关键技术的研究显得至关重要。当前，已有大量文献对机器人移动避障进行了相关研究。文献[2-3]通过寻找关键点来缩短机器人的行进路径，进而提升了其路径搜索效率。但该方法并未考虑路径的平滑处理及环境模型的建立，使得机器人在行进过程中并不流畅。文献[4]虽提出了多种不同类型的障碍物信息以指导机器人如何避障，但却未考虑与障碍物之间的最短距离，因此易与其发生碰撞。综上所述，文中提出了一种基于栅格精度的关键转折点选取方法。该方法既可提高节点的搜索效率，降低路径规划中的节点搜索个数，从而解决内存消耗问题；此外，还可通过转折点的平滑处理使得机器人行进路径更为平滑。

1 机器人移动路径规划算法

为了提升机器人的路线规划效率，首先需要基于环境采集传感器收集机器人工作场景的工况信息，再精确抽象出其工作环境的地图数学模型[5]。文中基于二维栅格法进行机器人的移动环境建模[6]，具体思路如图1 所示。

图1 机器人移动环境示意图

图1 中，每个栅格均具备二维平面的坐标属性。对移动机器人而言，算法关注的重点是该栅格是否可以同行。文中采用0-1 编码的方式，对机器人移动环境中的所有栅格Cell 进行编码，具体方式如下：

其中，0 代表可通行，在图1 中用白色表示；1 代表不可通行，图1 中用黑色表示。通过栅格编码，便可将环境模型存储在机器人系统中。

由于栅格精度也会对机器人行进路径造成一定的影响：栅格精度越高，其存储的环境量信息就越多，这便更容易干扰机器人的行进；反之，栅格精度越低，存储的环境量信息便越少，机器人也越容易碰到障碍物。因此，可通过引入栅格精度进行更为有效的路径规划[7-8]。具体的流程如下：

1）获取环境中的某一障碍物信息。

2）判断障碍物的外形，若该障碍物为凸形，便可将其划分为多个互不相交的三角形；若障碍物为其他形状，则计算其最大与最小顶点后，将该顶点作为矩形对角线，并通过计算矩形的面积，进而获得障碍物的面积。

3）根据面积公式确定障碍物的面积。

4）观察剩余的栅格中是否仍存在其他障碍物，若存在，则返回至步骤1）。

5）计算栅格的精度，其计算公式为：

式中，d为对应栅格的边长；Stotal为栅格的总面积且Stotal=∑i∈PS，S是障碍物的面积，P是障碍物集合，i则为其中某一障碍物。

2 改进的A*算法设计

2.1 A*算法优化

A*算法运行过程中的主要内存开销是OpenList、CloseList 这两个列表。在该算法的运行过程中，需随时计算所有的节点代价，并搜索列表中代价最小的节点进行替换。

图2 为机器人的行进路径图，其中灰色区域为A*算法在搜索过程中参与计算的节点。从图中可以看出，这些节点与最终的路径并无关联。但却消耗了计算机较多的计算与存储资源，且影响了算法的效率。此外，A*算法生成的路径还包含了诸如P1到P的不必要转折点，故影响了机器人的巡检效率。综上所述，需要对A*算法加以改进[9-10]。

图2 机器人行进路径图

该文提出了一种可以减少计算机内存消耗的方法，图中灰色代表需要计算的区域，*则代表规划的路线。可以看出，P1点到P点的直线距离最短，其仅需要计算两点间的距离。由于规划路径中存在过多的转折点，也会对机器人巡线造成影响，故该文通过寻找关键点来进行优化[11]。

为解决A*算法内存消耗过大，行进路径不平滑及行进过程中可能与障碍物发生碰撞的问题，此次优化将从以下几个角度进行：

1）在选择关键点时，尽量选择不靠近障碍物的点，以避免机器人在前进过程中发生碰撞。

2）经过转折点时，尽量将折线转变为曲线，使得机器人的行进路径更为平缓。

3）通过关键点的选取，降低机器人内存的消耗。

2.2 关键转折点选取

该文提出的关键点选取方法[12-14]如图3 所示，其中P1、P3分别是路径的起点和终点。在传统的A*算法中，需分别计算(1，2)、(2，1)及(2，2)这三个点的代价值，然后将代价最小的点(2，2)作为下一个父节点，并计算该节点周边所有点的代价值，再选择代价最小的路径。从图中可以看出，P1到P3存在一条最短路径，故仅需计算(2，2)、(3，3)、(4，4)与(5，5)这些点的代价即可。

图3 关键点选取原理示意图

关键点的选取可分为以下两种情况：

1）P1、P2和P3在一条直线上。

2）P1、P2与P3不在一条直线上。

针对上述两种不同情况，选取策略分别如下：

首先，若P1、P2及P3在一条直线上，则仅需保留起始点P1和终点P3即可；其次，P1、P2与P3是三个不在一条直线上的点，则又可分为以下两个步骤：①若P1、P2的连线与P1、P3的连接线均不与障碍物发生碰撞，删除P2；若P1、P3的连线与障碍物发生碰撞，则保留P1、P2及P3三个节点，再以P2为节点向下选取其他节点构成三角形。②以P2为起点继续选取其他节点，若选取的两个节点P3、P4与P5在同一条直线上，则删除P4并保留P3、P5节点，且重复该步骤直至到达终点。关键点选取过程，如图4 所示。

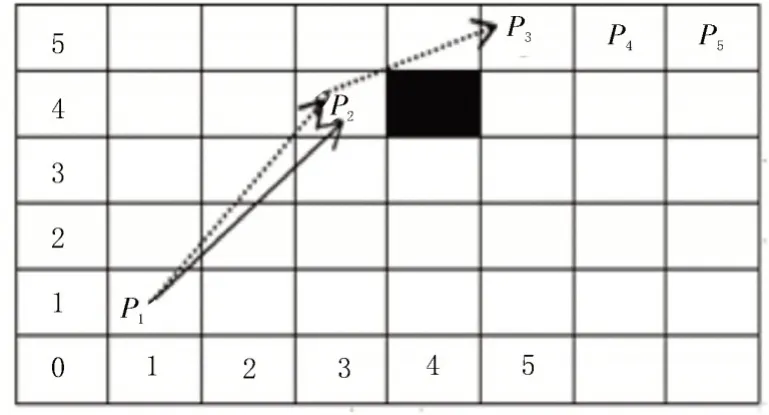
图4 关键点选取过程

在机器人行进过程中通常会遇到许多转折点，此时可将路径中的转折点记录在一个集合P中。转折点的计算如图5 所示，图中黑色方块为障碍物。从起始点开始依次连接各个转折点，并从集合P中再次选取关键转折点。通过定义评价函数G(x)，且将其作为最优转折点的选择依据，同时以设置权重的方式对评价函数进行重新定义，即：

图5 转折点计算

其中，α为调节参数，d1为障碍物中心到起始点、转折点连线的垂线长度；d2则为转折点到障碍物所在平面的垂线长度。

对每个节点基于式（2）计算其评价函数的值，然后对所有节点的评价值进行排序，再选取评价值最小的点作为转折的关键点。当引入关键点选取策略后，可大幅降低机器人行进路径中节点搜索的个数。

2.3 路径转折点选取及平滑处理

将选取的路径转折点进行平滑处理[15-16]，如图6所示。设MN点的坐标为(X1,Y1)、(X2,Y2)，OP点的坐标为(X3,Y3)、(X4,Y4)，A点的坐标则为(a,b)。其中BM与BN分别垂直于OA和AP，且两条垂直线相交于B点。原A*算法需经过的长度为L=L1+L2，具体的计算方法如下：

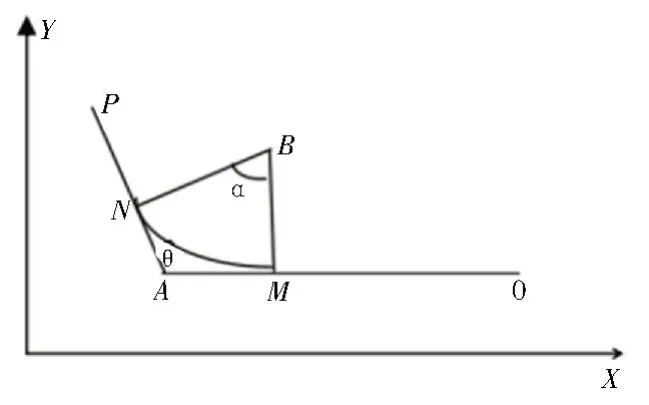
图6 路径转折点平滑处理

经算法改进后，原来的直线变为平滑曲线，L的距离也发生了变化。假设B点的坐标为(X，Y)，通过联立方程组可求解出圆的半径R。如图可知α角为π-θ，则利用式（6）可计算出半径为：

根据图6 联立上述的几何关系，可求得弧长MN为：

通过比较LMN与NA与MA距离的和，可发现路径长度显著减小。

3 算法仿真

为验证所提算法的准确性及可靠性，文中通过仿真实验将优化后的A*算法与传统算法进行比较。仿真实验在Matlab 上进行，具体的软硬件环境参数如表1 所示。

表1 软硬件环境参数

首先，利用二维栅格来对算法在二维空间的循迹性进行验证。在该二维平面中，通过坐标系构建现场环境情况，则机器人在二维栅格上进行的路径搜索过程，如图7 所示。

图7 在二维空间内的路径搜索示意图

从图7可以看出，算法写入机器人后，机器人便可完成二维平面下的路径循迹，同时实现自主避障功能。

为了进一步评估算法的性能，从机器人行进路径长度、转折点个数、与障碍物的最近距离以及时间四个方面对比该文算法与传统A*算法的性能。算法仿真结果，如图8-10 所示。

图8 传统A*算法路径

其中，图8 给出了传统算法下机器人的路径轨迹。根据式（2），改进A*算法的评价函数中，不同的α取值会影响算法的路径规划。图9-10 则给出了不同α值下机器人的行进路径。

图9 α=0.75 时，改进A*算法的路径

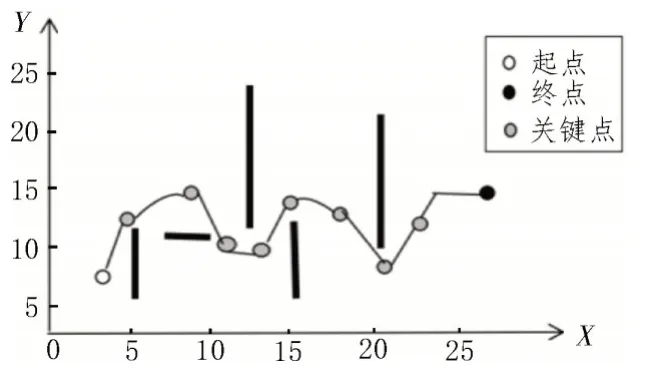
图10 α=0.5 时，改进A*算法的路径

由上图可知，传统算法下机器人的行进路线转折点过多，路径也并不平滑，且极易与障碍物发生接触。而改进A*算法在对关键点进行平滑处理后，机器人的行进变得更为平缓。此外通过对比不同α取值下的路径可知，α越大，机器人的行进便越平滑。

在上述场景下，具体的指标计算结果如表2所示。

表2 传统算法与改进算法结果比较

从表2可以看出，随着α的增大，改进A*算法的性能也在不断改善。同时机器人的路径长度由61.326 2 m缩短至56.527 6 m，相较于传统A*算法降低了1.80%；而算法的转折点个数由9 个减少至6 个，相较传统算法降低了40%；机器人的运动时间则由0.133 s 降低至0.091 s，相较于传统的A*算法下降了10.78%。此外，α的取值还会影响机器人与障碍物的最近距离。且当α较小时，机器人与障碍物的距离较远，不易发生碰撞。因此，算法可根据机器人对于安全性和运行速度的要求，合理选择α值。

通过上述实验可知，传统A*算法规划的机器人行进路径存在过多转折点及路径不平滑等问题。而与其相比，所提算法的路径更短，转折点较少且路径也更为平滑。同时在该算法中，根据参数α的不同，可以调整对行进路径、障碍物距离与运行时间的侧重，相较于传统A*算法有一定的提升。

4 结束语

该文提出了基于栅格精度的关键转折点、路径平滑处理方法，来对传统A*算法进行了改进。利用关键点方法可降低计算机内存的使用情况，而路径平滑处理则能解决机器人行进过程中转折点过多的问题。同时，通过加入障碍物计算方法，还确保了机器人行进过程中不会触碰到障碍物。基于多因素的移动机器人避障算法能够缩短机器人的行进路径与运行时间，并提升行进路线的高效与合理性。实验结果表明，改进后的A*算法比传统的A*算法更具优势。