基于元学习和K均值聚类的高分遥感影像变化检测

许自昌

(1.中国地质大学 资源学院,武汉 430074;2.福建省地质测绘院遥感中心,福州 350011)

0 引言

地表覆盖变化检测与信息提取是测绘、规划和土地等相关机构和职能部门日常工作的基础环节,对提升城市管理水平、促进土地集约利用、改善人居环境具有重要意义[1-2]。随着遥感数据获取技术的不断进步,高分影像数据成为包括地表变化检测在内的各种应用的主流数据源,但空间分辨率提高使高分影像的光谱异质性增大,“同物异谱”“异物同谱”、阴影与细小地物对信息提取的干扰更为严重,基于高分影像的变化检测也更具挑战性[3]。

基于机器学习的方法是当前变化检测领域的研究热点,但是面对复杂多变的高分影像场景,单一的分类算法和固有的优化策略在高分影像变化检测中并未展现出良好的泛化性能,难以适合用于所有类别的地表变化信息提取。近年来部分学者采用集成学习算法进行土地利用和土地覆盖信息提取[4-6],均取得了较理想的检测效果。集成学习是指对若干个个体学习器进行训练,再采用一定的结合策略,充分利用各学习器的特性,形成一个强学习器。集成模型构建过程一般包括个体学习器生成和学习器组合输出两个步骤。常用的个体学习器生成策略有boosting[7]、bagging[8]、RSM[9]。boosting策略是通过算法迭代提升个体学习器精度,以加权平均形式输出学习器组合模型的集成方案,更关注偏差降低。相较boosting策略,bagging更关注降低方差以增强个体学习器的多样性。而RSM的特征空间抽取是比boosting的数据重赋权和bagging样本抽取更有效地提升基学习器多样性的策略。学习器组合方法可分为全员组合法和选择组合法两类。选择组合法的相关研究较少,常用的全员组合法有投票法[10]、基于D-S证据理论的方法[11]、基于元学习的方法[12]等,其中元学习算法是一类将个体学习器产生过程和组合过程相结合的策略,通过将人工先验知识获取的手工特征翻译为机器更易理解的抽象特征,对原始训练集进行特征重构或合并,提升数据集的线性可分性。部分研究表明当原始数据特征维度较低时,将原始特征集与初级学习器产生的特征集组合重构,可拟合效果更佳的次级学习器判别模型。

鉴于此,本文从监督变化检测算法的时间复杂度角度切入,提出一种基于元学习同/异质混合集成和K-means聚类分析的兼顾算法精度与效率的高分影像变化检测模型,利用K-means聚类分析完成堆叠的训练集分割出训练子样本集,提供多元次级学习器提炼输出层的最终决策边界,并利用双重约束滤波优化初检结果,从算法运行效率、泛化性能和检测精度3个维度确保变化检测结果鲁棒可靠,为相关领域研究与工程实践提供新的技术实现途径,具有重要的理论意义与应用价值(图1)。

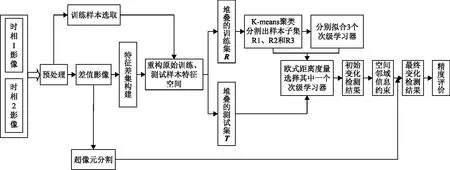
图1 基于元学习和K-means聚类的变化检测

1 研究方法

本文选用梯度提升树、随机森林和极端随机树作为元学习的初级(组件)学习器。先通过5折交叉验证分别训练各组件学习器,并对原始训练集和测试集进行预测,将各组件学习器的概率预测标签作为抽象特征与原始样本集的手工特征进行组合重构,再通过K-means算法对重构的训练样本集进行聚类分析,得到K个重构训练样本子集拟合逻辑回归算法,输出多元次级学习器,完成分类器混合集成模型的构建,最后测试阶段首先度量重构测试样本集中每个待分类像元与K个聚类中心的欧式距离,就近选择判别像元的次级学习器完成最终分类。

1.1 基于K-means聚类和元学习的变化检测算法

1)基于交叉验证的样本集特征空间重构。为提升元学习的泛化能力,避免过拟合现象,通过交叉验证的形式分段训练初级学习器进行样本集特征空间重构。交叉验证元学习算法流程如下。

设原始训练样本集RO为N×P维矩阵(N个样本,每个样本有P维特征),原始测试样本集EO为M×P维矩阵,初级学习器(算法)为{Y1,Y2,…,YQ}(其中1,2,…,Q代表不同的初级学习器算法),次级学习器(算法)为L,元学习集成模型的目标就是通过初级学习器将RO和EO分别重构为N×(P+Q)维的堆叠训练样本集RF和N×(P+Q)维的堆叠测试样本集EF,然后基于RF拟合次级学习器L,最后通过L处理EF输出集成模型最终判别结果。

单种初级学习器的样本集交叉验证重构过程如图2所示。首先对原始训练样本集RO进行5折划分,复制5组大小相同的样本集(图2上部),每组样本集包括1折临时训练集(4份蓝色训练集构成)和1折临时测试集(1份橙色测试集),前者的样本数是后者的4倍;其中,5组临时测试集(橙色)互不重叠。利用第1折临时训练集拟合初级学习器算法Y1得到分类模型M11,并通过M11预测该折临时测试集和原始测试样本集的标签,分别得到A11和B11,A11对应的位置索引为原始训练样本集中的后N/5条样本。同理分别采用另外4折样本集训练-测试得到A12、A13、A14、A15并结合A11构成N×1维特征,将新特征加入RO构成新的训练样本集Rs(N×(P+1)维)。相应地,将B11、B12、B13、B14、B15组合成5维特征,计算它们的均值,产生M×1维新特征加入原始测试样本集EO中构成新的测试样本集Es(M×(P+1)维)。至此完成第一种初级学习器算法Y1的特征重构过程,同法获取另外Q-1种学习算法的重构特征,组合最终的堆叠训练样本集RZ和堆叠测试样本集EZ,通过RZ训练次级学习器对EZ进行最终判别。

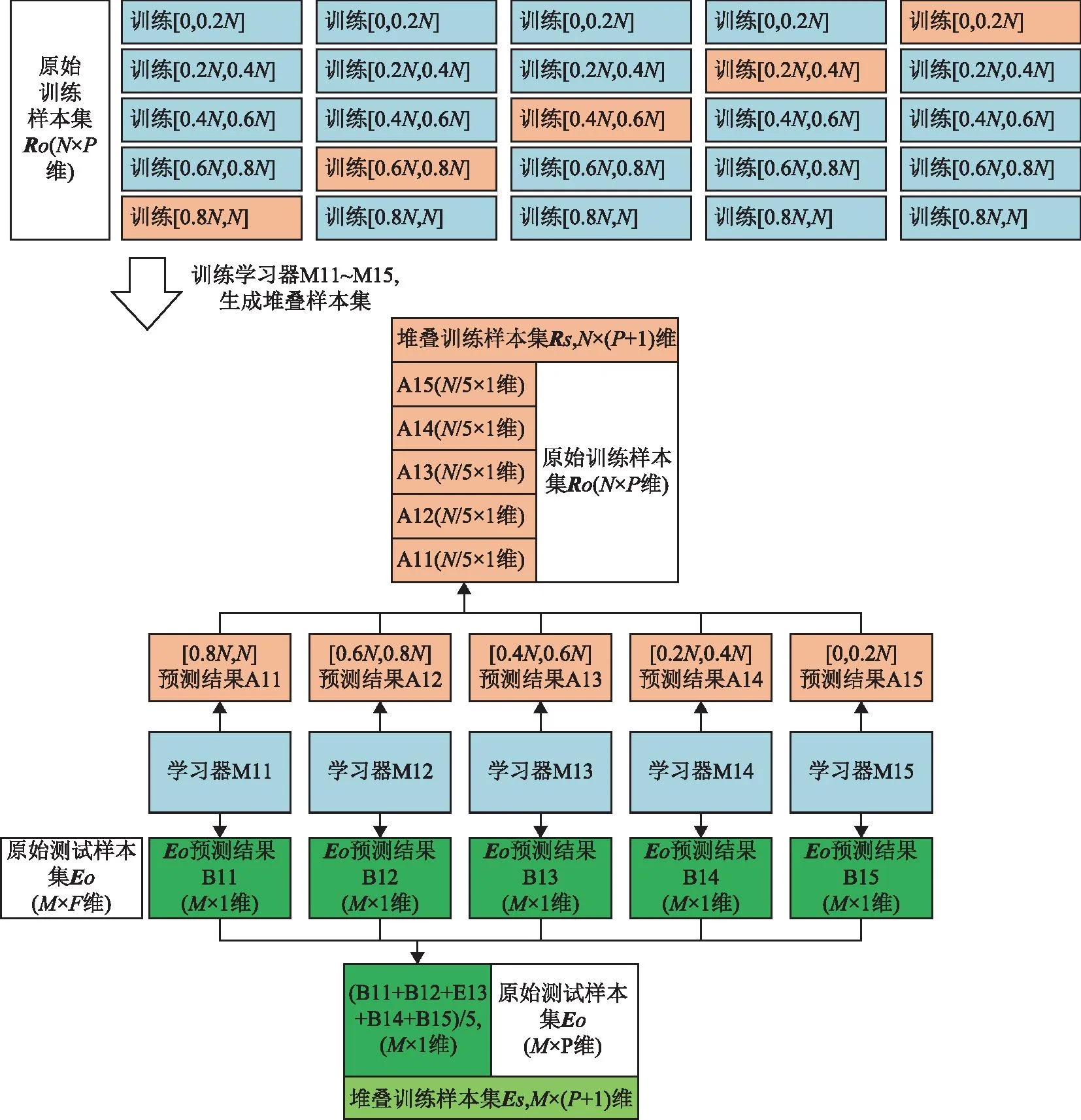
图2 基于5折交叉验证的元学习初级学习器生成过程

2)初级学习器的选择。为权衡算法效率、泛化性能和分类精度,保证元学习集成模型的变化检测结果鲁棒可靠,本文综合利用集成学习中的boosting和bagging的优点,选用梯度提升树(gradient boosting decision tree,GBDT)、随机森林(random forest,RF)和极端随机树(extreme random tree,ERT)3种集成算法构建元学习的初级层。

①梯度提升树。GBDT是集成学习提升策略的代表算法,可用于处理回归和分类问题,但基学习器都仅采用CART回归树。由于大多数损失函数的优化过程较为复杂,Friedman[13]提出通过求解损失函数的负梯度来逼近损失函数值最优解的优化方案,拟合回归树构建新的集成模型。基于此更新基学习器,可以降低基学习器的偏差,提升集成模型精度,本文选用GBDT作为元学习混合集成模型的一种初级学习器。在变化检测二分类中,GBDT选用二项似然函数构建损失函数,然后计算它的负梯度值gm(xi),并通过gm(xi)拟合一棵包含J个叶节点的CART回归树,最后通过更新强学习器输出最终集成模型FM(x)。

在测试阶段,对于任一待分类像元xt,集成模型对其的预测值为p=FM(xt),通过二项似然对数将预测数值映射为二分类概率标签。由式(1)计算出变化像元xt的概率P+(xt),则可判别未变化像元的概率为1-P+(xt)。

(1)

②随机森林。bagging策略中最常用的算法是随机森林,本文选用C4.5决策树作为RF的基学习器。RF基于bagging的自主采样策略,在运算过程中由于随机过程的引入,RF的算法运行效率和泛比性能显著提升,且对数据缺失不敏感,因此bagging是一种非常高效的集成策略。

③极端随机树。ERT是一种随机森林的变种算法。ERT中沿用RF中的自助采样和随机特征子集策略,在决策树拟合过程中,仍然通过信息增益率搜索每层决策树桩的最佳分裂特征fi,但分裂特征值si则是在原始样本集中特征f的所有取值里随机选择一个。由于ERT在生成过程中引入更多的随机过程,在集成模型泛化性能方面通常优于RF。

3)基于K-means聚类分析的多元次级学习器。本文选用boosting算法(GBDT)和两种bagging算法(RF和ERT)构建元学习算法的第1层,重构原始样本集特征空间,快速提升样本的可分离性。经上述混合集成处理后,原始训练样本集RO(N×P维)和测试样本集EO(S×P维)被转换为堆叠训练样本集RZ(N×(P+3)维)和堆叠测试样本集EZ(S×(P+3)维)。通常元学习的第2层利用RZ拟合一个次级学习器L(如线性SVM、逻辑回归等),对EZ进行最终判别。为提升集成模型的精度,本文在次级学习学习器生成过程中引入K-means聚类分析,构建多元次级学习器提炼输出层的最终决策边界,过程如下。

(2)

步骤4:将P1、P2和P3作为K-means算法的初始聚类中心,对堆叠训练集RZ进行聚类分析,算法迭代结束时RZ被分割为3个子集RZ1、RZ2和RZ3,聚类中心更新为Q1、Q2和Q3。

步骤5:基于RZ1、RZ2和RZ3分别拟合3个逻辑回归分类器L1、L2和L3,构建元学习的输出层(次级学习器)。

步骤6:在分类阶段,对于堆叠测试样本集EZ中的任一待检测像元u,首先计算它和Q1、Q2和Q3的欧式距离,根据就近原则选取相应的逻辑回归分类器对其进行标签判别。

步骤7:采用双重约束滤波优化检测结果。

1.2 双重约束滤波优化处理

简单线性迭代聚类(simple linear iterative clustering,SLIC)超像素分割算法[14]是对K-means的一种改进算法,算法复杂度较低,且分割所得的超像素块能较好地保持与地理实体的边缘一致性。SLIC算法中的K值用于指定生成的超像素块数。本文按照Chen等[15]将SLIC超像素分割算法与高分影像空间邻域信息相结合构建双重约束滤波,优化集成模型的监测结果,减轻以像元为处理单元所产生的“椒盐噪声”,降低变化检测误检率和漏检率,提升检测精度。双重约束滤波优化过程如下。

步骤1:对双时相影像的差值影像D进行SLIC分割。

步骤3:遍历步骤2处理的二值影像中的所有像元,统计每个像元空间八邻域的像元标签,若变化像元数量大于等于6,则将邻域中心像元设置为变化类别,产生最终的变化检测结果图。

双重约束滤波优化通过步骤2分割对象边界约束可有效抑制基于像元的检测方案所产生的“椒盐噪声”,降低变化检测误检率。通过步骤3挖掘空间上下文邻域信息,可有效减少基于像元的检测结果中的地理实体内部破碎现象,使检测结果更加完整,降低变化检测漏检率。

2 实验

2.1 数据源

本文选用WorldView-2和SPOT 5两组双时相高分影像为数据源(图3),两组数据源均通过ENVI 5.2进行数据预处理,处理内容包括辐射定标、大气校正、几何校正和G-S融合。SPOT 5影像包含绿、红、近红外、短波红外和全色共5个波段,全色波段为2.5 m。两景影像成像时间分别为2006年12月和2007年12月,区域位于广东省清远市,影像大小为512像素×512像素,主要变化为水体变成裸地,以及裸地变为植被。WorldView-2影像包含红、绿、蓝、近红外和全色共5个波段,全色波段为0.5 m,多光谱波段均为1.8 m。两景影像的成像时间分别为2012年11月和2016年10月,区域位于福建省福州市,影像大小为1 800像素×1 300像素。主要变化是植被、裸土和建设用地三者之间的转换。

图3 变化检测的原始影像

2.2 实验结果与分析

首先,对预处理后的双时相影像的差值影像提取每个波段的光谱特征、GLCM 纹理特征和形态学特征,构建原始训练样本集,其中数据集1的纹理特征,方向设置为0°,扫描窗口大小为3像素×3像素,灰度量化等级为16;数据集2纹理特征的扫描窗口为5像素×5像素,其他参数设置同数据集1。两个数据集的形态学结构算子均设置为圆形,扫描窗口为3像素×3像素。其次,通过提出的结合元学习和K-means的方案(MK,空间约束处理后为MK-SC)分别对两组数据集堆叠重构进行变化检测。对比算法包括GBDT、RF、ERT和HCM-SC[16]。

随着基学习器数量的迭代增加,不同集成方法的学习曲线如图4所示。从图4可以看出,对于数据集1,GBDT、RF、ERT和MK的最佳基学习器个数分别为41、54、68和51,相应的错误像元数为8 658、9 504、9 164和6 095。数据集2相应的最佳基学习器个数和错误像元数分别为45、74、87、63以及167 565、174 236、160 807、101 473。算法HCM-CS对于两组数据集的最佳基学习器个数分别是60和70,错误像元数分别为5 306和89 248。在算法迭代初期,随着基学习器数量的增加,4种变化检测方法的错误像元数均迅速降低。由于采用了最速下降法优化参数,两组实验中GBDT算法收敛时基学习器数量均少于对比算法,由于ERT在决策树叶节点分裂阶段比RF引入了更多的随机过程,基学习器的多样性随之增强,因此需要更多基学习器(决策树)来改善集成模型精度。两组数据集中ERT的收敛决策树棵树大致为65和81,RF的收敛棵树大致为50和68,且ERT的收敛精度均优于RF。本文算法综合GBDT、RF和ERT 3种算法的特性,并通过交叉验证和K-means聚类分析降低过拟合风险、提升算法精度,两组数据集中MK的基学习器数量分别在50和60左右算法进入收敛。相较元学习集成前的3种算法,本文方法误检像元数最少。

图4 不同基学习器个数下4种集成方法的学习曲线

表1展示了5种算法到达最佳变化检测精度时(最佳基学习器个数)的运行时间。两组数据集中,bagging系列算法(RF和ERT)的运行效率均优于GBDT;虽然ERT算法需要比RF算法更多的基学习器才能收敛至最佳精度,但由于决策树生成过程中更多随机过程的引入,ERT算法拟合单棵决策树的平均时间和算法运行总时间都小于RF。本文提出的MK算法时间复杂度显著低于HCM-SC。

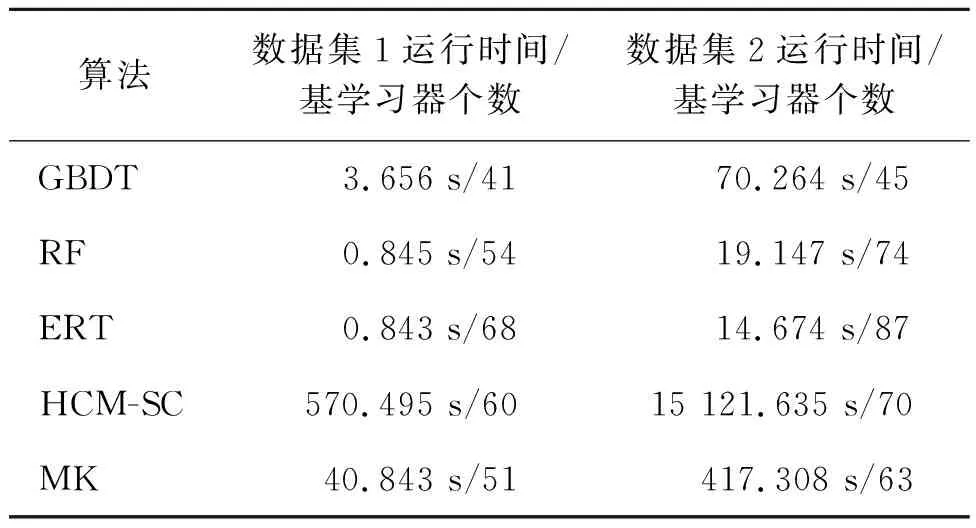
表1 5种算法到达最佳变化检测精度时(最佳基学习器个数)的运行时间

从图5、图6可以看出,两组数据集中未经空间约束处理的4种方法(GBDT、RF、ERT和MK)的检测结果均有“椒盐噪声”和不同程度的地理实体内部破碎现象。对于3种同质集成算法(GBDT、RF和ERT),综合4种评价指标,数据集1的最优检测算法是GBDT,针对影像中大面积水域变化以及东南侧裸地到植被变化的检测结果较为完整。ERT的总体精度略优于RF,但漏检现象多于GBDT。由于数据集2的场景较为复杂,GBDT算法通过贪心策略寻求最优解,产生大量漏检现象。相较而言,RF和ERT引入随机过程使基学习器的多样性大幅提升,检测结果总体优于GBDT,其中随机过程更强的ERT表现出可观的检测效果,4种评价指标均优于RF。因此适当提升基学习器的多样性、增强学习器之间的差异可提升复杂场景的变化检测效果。此外,3种同质集成算法在两组数据集中均有大面积的漏检区域和较多的误检碎斑,数据集1的漏检区域主要集中在影像东北侧裸地到植被的部分伪变化和阴影区域。数据集2漏检区域主要为影像西北部和南部从植被-裸地混合区域到建设用地的转换。

图5 数据集1变化检测结果

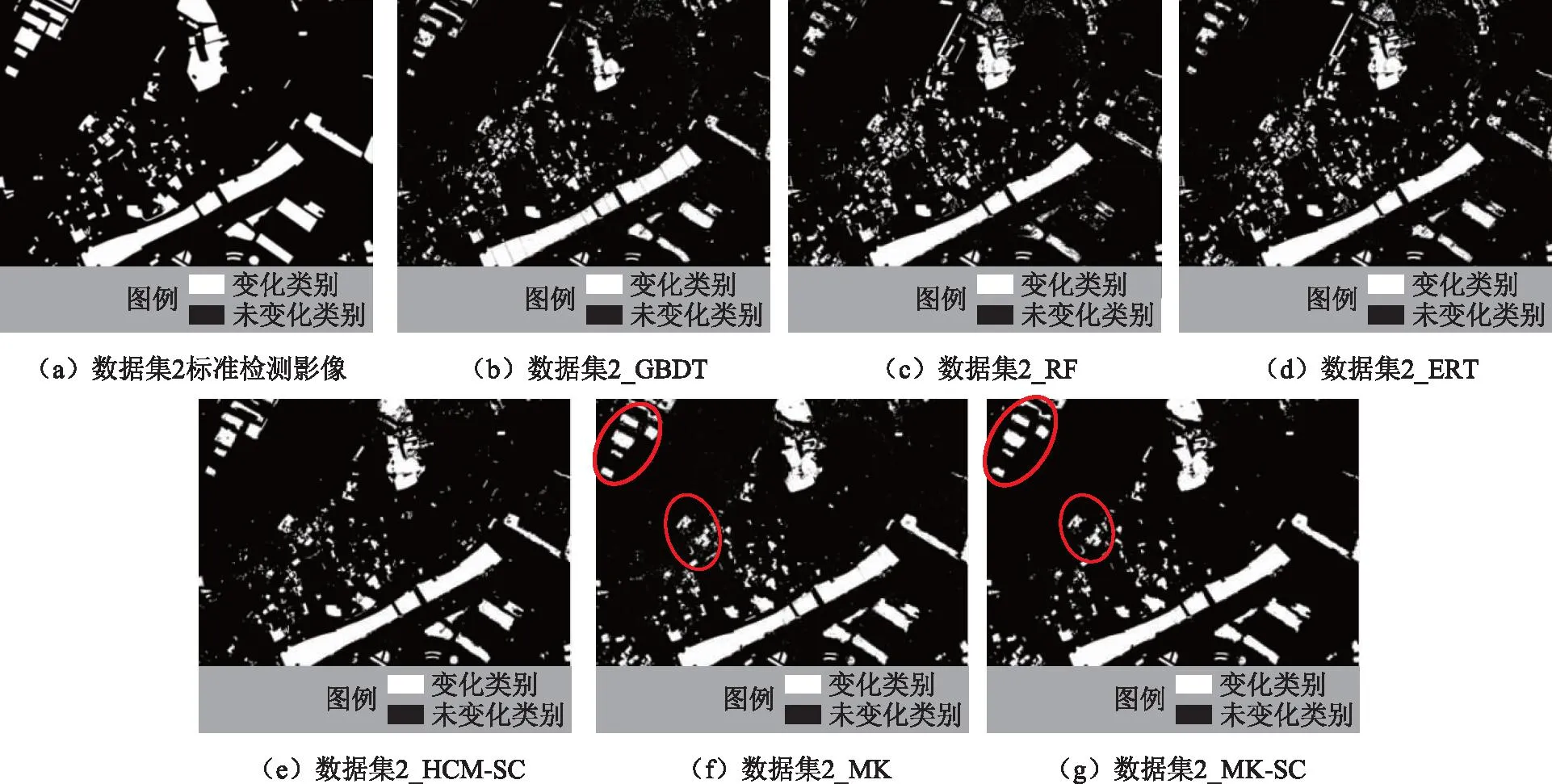
图6 数据集2变化检测结果

本文提出的元学习-聚类分析混合集成模型(MK)综合3种同质集成算法的特性,检测结果中误检和漏检现象得到明显改善,4种精度评价指标均优于混合集成前的同质算法。经空间约束优化后(MK-SC)的检测结果中大量“椒盐像元”被滤除,总体精度和误检率得到改善,但由于部分被正确检测的细小地物以及地理实体内部的少量不连续像元被“误删”,如表2、表3所示MK-SC的漏检率相对于MK有略微提升(数据集1为0.132 1和0.128 3,数据集2为0.215 2和0.201 0)。值得说明的是,本文构建的混合集成模型的综合精度评价结果仅略低于HCM-SC算法,但算法运行时间却大幅缩短,MK对于两个数据集的处理耗时分别为40.843 s和417.308 s,而HCM-SC对于两个数据集的处理耗时分别为570.495 s和15 121.635 s。

表2 数据集1变化检测精度评价

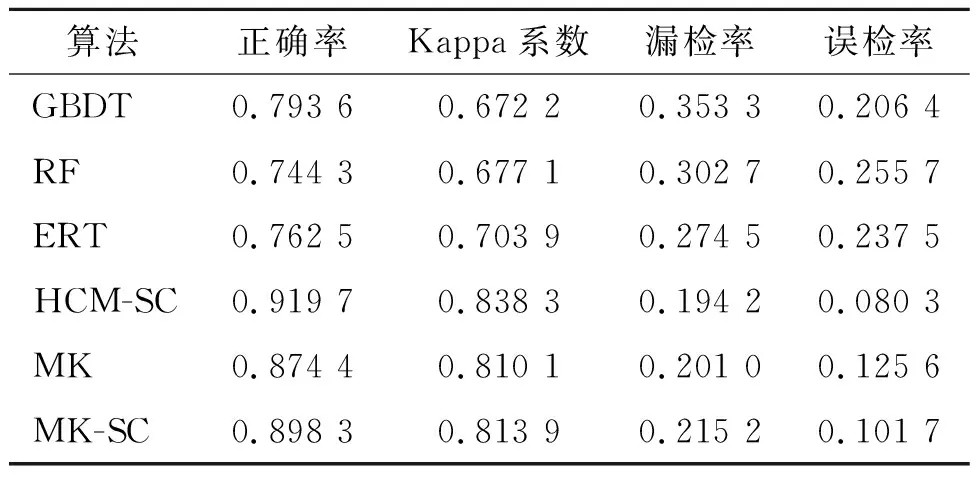
表3 数据集2变化检测精度评价

3 结束语

本文结合元学习和K-means聚类分析实现的混合集成高分影像变化检测算法通过快速重构原始样本集特征空间、增强数据集的线性可分离性,在保证泛化性能和检测精度的同时提高了分类效率,为变化检测提出新的研究思路,结论如下。

1)元学习算法可对不同策略的同质集成算法(boosting和bagging)进行混合异质集成,在降低基学习器的偏差的同时也能降低基学习器的方差,是一种处理集成学习中基学习器精度-多样性权衡难题的有效途径。

2)通过交叉验证策略进行元学习的堆叠样本集重构,可有效避免算法过拟合风险。而通过K-means聚类分析提炼元学习输出层的决策边界,构建多元次级学习器的元学习混合集成模型能有效处理复杂场景变化检测任务。

3)元学习混合集成策略的变化检测精度虽然略低于HCM-SC算法,但前者的算法运行效率显著优于后者,更适合用于海量时序高分遥感数据源的变化检测工作。

本文提出的基于元学习同/异质混合集成和K-means聚类的高分影像变化检测方法可在较高检测精度下大幅缩减集成算法的运行时间,从算法运行效率、泛化性能和检测精度3个维度确保变化检测结果鲁棒可靠,但针对建筑物密集的复杂地表,检测结果仍有待提升。同时,如何合理选择异质弱分类器并针对其特定的组合构建高效、鲁棒的集成策略,如何将该方法拓展到多类变化检测样本自动选择均是后续研究的重点和努力的方向。