范德瓦耳斯体系中的量子层电子学*

肖聪 姚望

1)(香港大学物理学系,香港 999077)

2)(澳门大学应用物理与材料工程研究院,澳门 999078)

二维范德瓦耳斯材料因其新颖的平衡态性质、电磁输运和光学响应性质而成为当前凝聚态物理研究的热点.不同于三维体材料,二维材料在厚度方向不具有晶格周期性.原子级平整的单层体系在厚度方向以范德瓦耳斯力结合,不同层的电子波函数因此混合起来,使得电子态的层分布不再仅仅是一个离散的空间变量,而同时成为一个量子力学量.层指标 (layer index)因而成为标记电子态的一个新量子数,为层状材料所独有.在最简单的两层体系中,层间范德瓦耳斯耦合可以类比于固体电子的自旋轨道耦合引起的自旋杂化;后者混合了自旋向上和向下的电子态,而前者是上层和下层的杂化电子态.基于这种类比,层自由度也被称为层赝自旋 (layer pseudospin).自旋-层赝自旋类比意味着自旋电子学的基本概念和理论构想可以迁移到范德瓦耳斯材料电子特性的研究,并且层赝自旋的面外分量对应电偶极矩,同电场直接耦合,与自旋和谷赝自旋的磁偶极矩互补,这些前景带来了层赝自旋电子学 (layer pseudospintronics)或称为层电子学 (layertronics)这一研究领域的发展[1,2].例如,电子体系中多体相互作用可以导致平衡态自旋铁磁性,而理论指出在双层石墨烯体系考虑多体效应也可以出现层赝自旋“铁磁性”[3],对应铁电性,即电子态层分布的对称性发生破缺,电荷分布出现自发层极化(这种传导电子的自发层极化,与二元化合物二维半导体中因为不同原子的电子亲和能差异导致跟堆垛关联的束缚电子的层极化有所区别).自旋电子学逻辑电路中著名的自旋阀效应和自旋场效应晶体管在层电子学中的对应,即双层赝自旋阀和双层赝自旋场效应晶体管,也已在双层石墨烯体系和双层MnBi2Te4中被提出[4–6].在电子输运方面,磁场与电子自旋的耦合可以在非磁金属体系中引起霍尔效应[7,8],甚至引起非磁性金属到陈绝缘体的相变,导致出现量子反常霍尔效应[9];而最近的实验和理论研究表明,在反铁磁范德瓦耳斯金属体系中,门电压与层自由度的耦合也会引起霍尔效应[10,11].理论也在反铁磁范德瓦耳斯材料MnBi2Te4中预言了门电压导致的量子反常霍尔绝缘体[12].

考察上述工作,有以下两方面特别值得注意.

1)虽然这些层电子学效应在理论概念上存在自旋类比,但由于层自由度的电本质(电荷的层分布和层极化)及其独有的空间可分辨特性,它们导致的物理现象和应用潜力可以超出自旋电子学的范围.比如门电压取代磁场使得范德瓦耳斯材料成为实现全电调控霍尔和量子霍尔输运的重要探索平台.又比如当二维材料组装成范德瓦耳斯异质结或同质结时,每一单元层上的电学输出有可能被单独测量.因此即使该范德瓦耳斯体系没有净霍尔电压,体系中每一层上的霍尔效应,即层霍尔效应(layer Hall effect)[10]依旧可以产生电霍尔输出.

2)植根于动量空间层赝自旋结构为范德瓦耳斯体系的电子波函数所特有的量子几何性质,还未被充分研究.在自旋电子学中,自旋轨道耦合将自旋这一内禀自由度和动量空间物理耦合起来,使得电子态自旋成为动量空间中的变量,形成材料体系中丰富的动量空间自旋结构.基于自旋-层赝自旋类比,层间耦合可以导致范德瓦耳斯体系中非平庸的动量空间层赝自旋结构 (layer pseudospin texture).动量空间自旋结构导致电子波函数非平庸量子几何性质,不仅表现为自旋轨道耦合体系中非零的动量空间贝里曲率,引起反常霍尔效应,而且导致扩展的波函数参数空间——动量-磁场空间中的混合贝里曲率 (mixed Berry curvature),引起自旋磁电响应、自旋轨道转矩以及磁非线性反常霍尔效应等重要现象[7,13,14].与之对应,动量空间层赝自旋结构不仅可以导致动量空间贝里曲率,也可以导致层状体系特有的波函数参数空间——动量-门电场空间中的混合贝里曲率.这两类能带几何量描述了动量-门电场参数空间中的量子几何性质,是层自由度量子力学本性的体现.对它们导致的物理效应的研究即开启了量子层电子学 (quantum layertronics)这一层电子学的新兴方向.动量空间量子几何相关的物理是近年来范德瓦耳斯体系新奇输运效应研究的基础,包括贝里曲率偶极子 (Berry curvature dipole)和贝里联络极化率 (Berry connection polarizability)产生的非线性霍尔效应[15,16];而动量-门电场空间中的量子几何效应为范德瓦耳斯体系所独有,可能引起在三维体系中前所未见的物理效应,为量子材料调控和器件应用提供新思路,却尚未得到足够重视.

作为动量-门电场空间新奇量子几何效应的例子,最近的一个理论工作指出动量-门电场空间中的混合贝里联络极化率可以诱导出范德瓦耳斯材料中一种新颖的交叉非线性动力学霍尔效应 (crossed nonlinear dynamical Hall effect)[17].不同于过去研究的非线性反常霍尔效应[15,16],该效应不是由单一电场驱动,而是由面内电场和门电场共同驱动,这一非常规的非线性霍尔构型却更切合逻辑电路设计的需求.双驱动场构型还使得通过调节驱动场的相位差来调控霍尔输出成为可能,带来一种相位差调控的非线性霍尔整流机制,为可控整流器件的设计提供了新思路.该效应以门电场的时间变化率作为面外驱动,可以在非磁性层状体系中实现只依赖于材料内禀能带结构的所谓内禀非线性反常霍尔效应 (intrinsic nonlinear anomalous Hall effect),是电驱动非磁性材料内禀反常霍尔效应的第一个理论建议.不仅如此,这一效应的手征晶格对称性要求与转角双层 (twisted bilayer)体系完美适配,成为该体系的一个特征非线性输运效应,揭示了转角石墨烯和转角过渡金属硫化物在非磁金属态隐藏的量子几何特性.在转角双层石墨烯和转角双层二碲化钼中,尤其当转角较小从而层间杂化效应显著时,理论预言在低掺杂情形即可产生0.01 至1个量子电导的霍尔导[17].考虑到层间杂化效应强的能带宽度大约在 10 meV 量级,该效应预期在几十开尔文温度下都比较显著.这个例子显示出量子层电子学富含的潜力,它不仅可以提供范德瓦耳斯体系中前所未见的非线性电子学 (nonlinear electronics)和转角电子学 (twistronics)效应,而且可以提供新的材料刻画工具和电学器件设计思路.

这个工作揭示的交叉非线性霍尔机制还可以扩展到磁性范德瓦耳斯金属材料.在有磁性的情况下,不仅交流门电压可以导致动力学非线性霍尔效应,直流门电压也可以导致直流非线性霍尔效应.支配这个效应的也是动量-门电场空间中的混合贝里联络极化率.这个新的理论观点可以自然地理解实验观测到的反铁磁偶数层金属态MnBi2Te4中门电场诱导的霍尔电流[10],并为寻找支持该效应的更广泛的范德瓦耳斯材料体系提供了理论框架.另外,在磁性范德瓦耳斯金属态,最近的理论研究还预言了由动量-门电场空间量子几何性质决定的另一种新颖非线性响应.由于动量-门电场空间的混合贝里曲率偶极子的存在,一个宏观面外电极化会出现在体系对面内驱动电场的二阶响应之中[18].

除了贝里曲率物理,量子层电子学还可以探测范德瓦耳斯体系更丰富的能带几何性质和随之而来的新奇物理效应.一个例子是非磁性转角双层体系中时间反演偶的线性霍尔效应[19].在这个效应当中,虽然双层体系的净霍尔流被昂萨格倒易关系禁止,转角体系的结构手征对称性依然可以在每一层提供霍尔效应需要的手性,而两层的霍尔效应手性相反,如图1(e)所示.这一效应的特别之处在于每一层上线性霍尔流的存在并不需要磁自由度,而需要破坏所有镜面对称性,由手征结构支持 (图2(a)).这些基本的对称性要求与反铁磁范德瓦耳斯体系中的层霍尔效应[10–12](图1(a)—(d))完全不同.后者是时间反演奇的效应,并不要求体系的结构具有手性.除此之外,时间反演偶的霍尔效应是一个费米面效应,并且要求费米面附近电子态具有层间杂化;如果电子态完全极化在某一层上,效应就会消失.这与反铁磁双层中时间反演奇的层霍尔效应完全不同 (图1(c),(d)).这一特点表明该效应植根于层自由度的量子力学特性,电子可以既不完全处于上层,也不完全处于下层,而是处于两层的叠加态上,态叠加的几率幅依赖于电子的动量.动量依赖的层叠加振幅导致动量空间中的层赝自旋结构(图2(b))和量子几何性质.文献 [19] 的理论分析表明,为这一量子效应负责的是一个新的能带几何量: 层电流在动量空间的反对称偶极子,也即层电流的动量空间旋度 (momentum-space vorticity of layer current).它代表层间杂化的范德瓦耳斯体系相邻层上的电流互相关联,关联的强弱与动量空间层赝自旋结构有关,当波函数层间杂化非常充分,层赝自旋完全躺在二维平面内时关联最强.

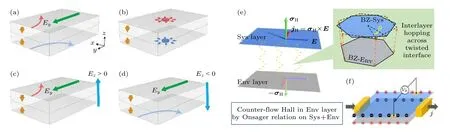
图1 双层范德瓦耳斯体系中时间反演奇和时间反演偶的线性层霍尔效应 (a)—(d)双层反铁磁绝缘体中时间反演奇的层霍尔效应,黄色箭头代表反铁磁自旋构型.(a)在面内电场 (绿色箭头)驱动下两层各自有霍尔电流 (红色和蓝色箭头),大小相等,方向相反.这是因为 (b)两层相反的动量空间贝里曲率 (红色和蓝色箭头).(c),(d)施加门电场 (蓝绿色箭头)会使霍尔电流只出现在一层之中,门电场反向则霍尔电流电流层分布相反.(e),(f)双层非磁性体系中时间反演偶的层霍尔效应.红色,绿色,蓝色箭头分别代表矢量关系 jH=σH×E 中的3 个矢量.(e)非孤立二维系统层 (sys layer,蓝色平面)和环境层 (env layer,灰色平面)之间的转角界面耦合会在二维非磁性系统层中通过时间反演偶的霍尔效应产生霍尔电流.而整个双层系统满足的昂萨格关系要求环境层中必然产生相反的霍尔电流.绿色阴影区域表示两层相对转角为 θ 时布里渊区之间的层间跃迁.(f)样品边界上电荷积累 (红色和黑色,+/–)导致的时间反演偶的霍尔效应的霍尔电压能够被层分辨的测量所探测,黑色箭头代表外加驱动电流,转载自文献 [12,19]Fig.1.Time-reversal (TR)odd and even linear layer Hall effects in van der Waals bilayers.(a)–(d)TR odd layer Hall effect in bilayer antiferromagnetic insulators.The yellow arrows denote the antiferromagnetic configuration.(a)The layer Hall counterflow in up and down layers,represented respectively by red and blue arrowed curves,driven by in-plane electric field (green arrow),due to (b)the layer-locked and-contrasted momentum space Berry curvature (the red and blue fluxes);(c),(d)when a perpendicular electric field (the cyan arrow)is applied,the system shows layer-locked anomalous Hall effects tunable by the electric-field direction.(e),(f)TR even layer Hall effect in nonmagnetic van der Waals bilayers.The red,green,and blue arrows denote the three vectors in jH=σH×E .(e)The twisted interfacial coupling between the system layer (Sys layer,blue plane)and an environmental layer(env layer,gray surface)yields a TR even Hall current in the system layer,whereas a counterflow Hall current is expected in the environmental layer,by Onsager relation on the whole structure: system (Sys)+environment (Env).Green shaded area denotes the interlayer hopping between the Brillouin zone (BZ)with twist angle θ .(f)The TR-even Hall voltage VH due to charge accumulation at the sample edges (red and black+/–)can be detected with a layer resolved measurement.Black arrows denote source and drain current j .Reproduced with permission from Refs.[12,19].

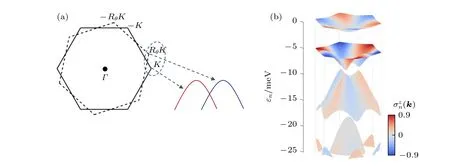
图2 转角双层过渡金属硫化物体系的超晶格mini 能带层赝自旋结构示意图(a)两层之间的相对转动导致来自不同层的带边在动量空间中的相对移动 (红色和蓝色曲线分别代表上层和下层的带边色散),同时也破坏了所有镜面对称性,导致手征结构;(b)层间量子隧穿将两层的带边杂化耦合成的mini 能带,图中展示的是2°转角下的能带,颜色标注 σz (层赝自旋的z 分量)在超晶格Bloch 态下的期待值,展示了层赝自旋在动量空间的纹理,由转角调控Fig.2.Schematics of layer pseudospin structure of twisted bilayer transition metal dichalcogenide: (a)The relative rotation between the two layers leads to the displacement of the degenerate band edges from the two layers (red and blue parabola)in momentum space,and breaks all the mirrors and results in a chiral structure;(b)interlayer quantum tunneling hybridizes the band edges from the two layers and form the superlattice minibands.An example at twisting angle of 2° is shown.Color denotes the expectation value of σz,the z component of layer pseudospin,under the superlattice Bloch state,which displaces a layer pseudospin texture that is controlled by twisting angle.

图3 展示了转角双层石墨烯体系里时间反演偶的霍尔效应.小角度时,在轻微掺杂的情况下该效应即十分显著.在中心能带处的霍尔比率,即霍尔角,可以达到1 的量级.随着转角增大,层间耦合的重要性减小,低能区的电子波函数层间杂化和霍尔效应逐渐减弱.然而文献 [19] 显示,当转角增大到最大公度角 (commensurate angle)θ=21.79°时,低能区的霍尔电导又增强到很大数值,如图2(c)所示.这一现象不能被常用的转角莫尔体系连续模型[20]所描述,而揭示出小尺度莫尔超晶格的晶格平移对称性对输运效应的影响.值得指出的是,类似的输运效应增强也在前述交叉非线性动力学霍尔效应中被发现[17],显示出公度莫尔结构的特性,以及大角度转角电子学不同于小角度情形的物理.

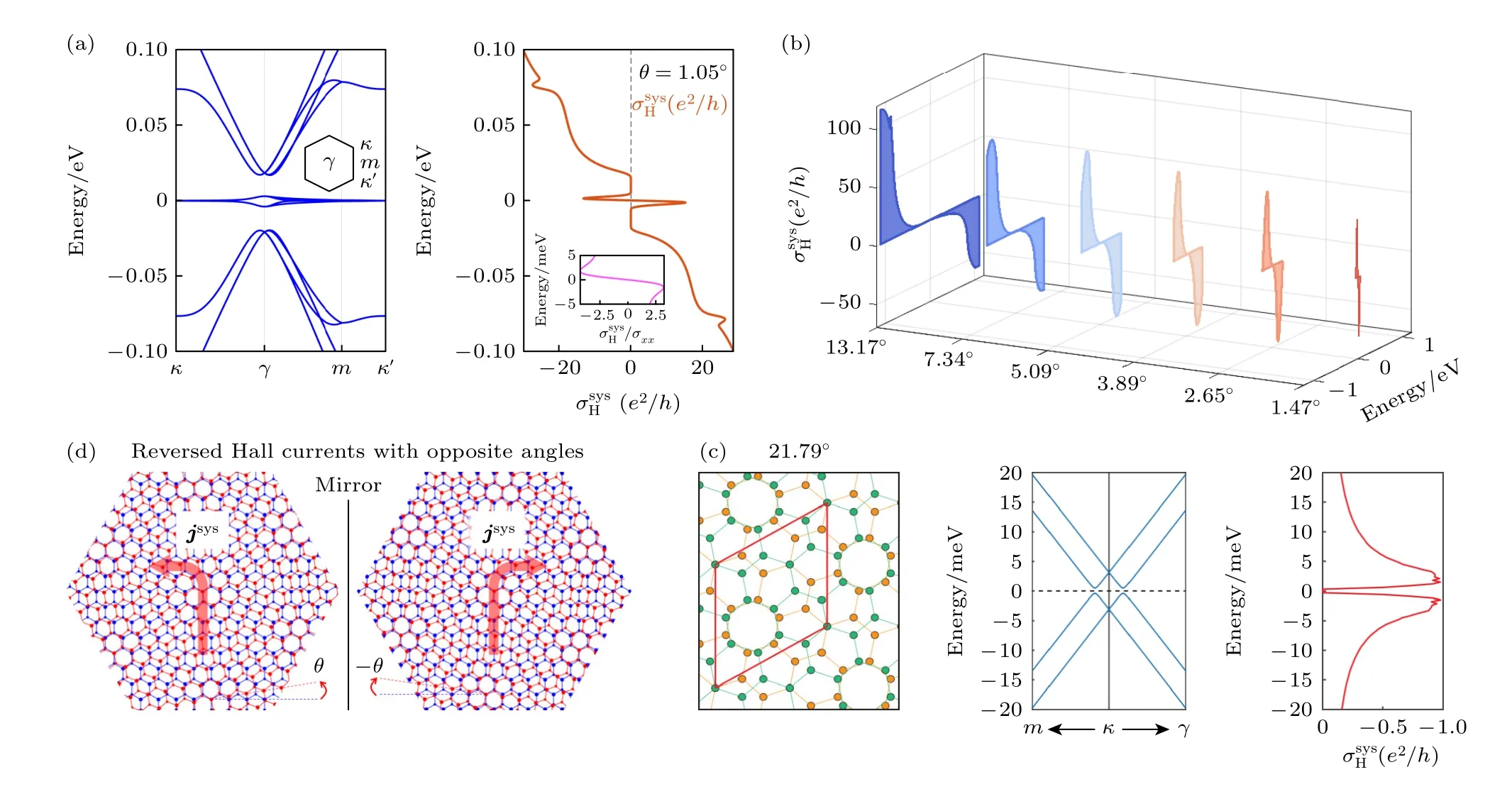
图3 转角双层石墨烯在不同角度下的能带结构和时间反演偶的霍尔电导率 (a)θ=1.05◦,插图描述的是化学势位于中心能带时霍尔电导率与纵向电导率σxx 的比值,即霍尔比率.(b)霍尔电导率的两个中心峰值随两层石墨烯相对转角的演化.考虑自旋简并度,这里霍尔电导率 要乘以2.(c)转角θ=21.79◦时的转角双层石墨烯结构(红色平行四边形围成的区域是一个莫尔原胞),狄拉克点附近的低能能带结构,和系统层中的霍尔电导率.(d)系统层中的霍尔流 jsys 会随着两层相对转角变号而反向.这是因为转角反号后的莫尔体系是反号前体系的镜像对称.在计算中取电子的弛豫时间为 1 ps.转载自文献 [19].Fig.3.Band structure and TR-even Hall conductivity for twisted bilayer graphene at different θ.(a)θ=1.05◦ .Insets: Hall ratio of Hall conductivity to the longitudinal conductivity σxx when the Fermi level is within the central bands.(b)Evolution of the two central peaks of with θ,here should be multiplied by a factor of 2 accounting for spin degeneracy.(c)Moiŕe of θ=21.79◦twisted bilayer graphene (the red lines enclose one unit cell),the low-energy band structure near the Dirac points,and the Hall conductivity in the system layer.(d)Schematics of reversed Hall currents in the system layer jsys by twisting in opposite directions,where the moiré lattices are mirror images of each other.In the calculations we take the electron relaxation time to be τ=1 ps.Reproduced with permission from Ref.[19].

交叉非线性动力学霍尔效应和时间反演偶的线性霍尔效应揭示了转角双层体系量子几何性质的不同侧面,并且可以用输运效应来探测它们.通过调节转角的方向和大小就可以调控霍尔效应的手性和强弱,图2(d)给出一种新的霍尔调控方式.

上面讨论的两个输运效应与范德瓦耳斯体系中的光学现象——圆二色性[21],即体系对垂直二维平面方向入射的左旋和右旋偏振光具有不同响应,都要求系统具有手征结构对称性.手征对称性还会引起转角双层体系中一种新颖的非线性光学效应: 垂直二维平面入射的圆偏振光诱导出面外电极化[22].该效应是自旋逆法拉第效应 (spin part of inverse Faraday effect)的层赝自旋版本,并揭示了光学响应中一个新的能带几何量——层间位移矢量(interlayer shift vector).这个几何量是非线性光学中熟知的几何量——位移矢量 (shift vector)[23]——在门电场参数空间中的对应.这些输运和光学效应的例子表明量子层电子学、转角电子学与手征电子学 (chiral electronics)的交叉包含丰富的物理,值得进一步研究.一个可能的方向是电学磁手征各向异性 (electrical magneto-chiral anisotropy)[24],即在具有手征对称性的体系中施加外磁场会使电阻随电流反向而变化,出现非互易输运 (nonreciprocal transport)效应.在自旋守恒的手征范德瓦耳斯体系,比如转角双层石墨烯和转角双层过渡金属硫化物,面内磁场影响输运只有通过和面内轨道磁矩耦合.而面内轨道磁矩的存在需要上下层相反的电流和层间量子跃迁构成电流回路,与转角双层体系时间反演偶的霍尔效应包含的物理内容直接相关.这种起源于层自由度量子力学特性的面内磁耦合[25]可以提供范德瓦耳斯材料中第一个不依赖于自旋自由度的电学磁手征各向异性机制.不仅如此,它还会引起线性和非线性反常平面霍尔效应(anomalous planar Hall effect),这些效应在二维材料中通常被认为只起源于自旋磁耦合[7,26].

上述磁输运效应与洛伦兹力无关,而依赖于范德瓦耳斯体系动量空间层赝自旋结构导致的面内磁电耦合.这自然引出另一个研究方向,范德瓦耳斯体系的面外磁电耦合和面外-面内正交磁电耦合[27,28].首先,在交叉非线性动力学霍尔效应的启发下,一个呼之欲出的效应是门电场时间变化率引起非磁性范德瓦耳斯体系的面外轨道磁化.在金属态,这又会导致新型的门电场引起的反常能斯特效应.该效应不同于通常的反常能斯特效应,不需要磁性材料和外磁场,可以为全电调控的非磁性热电器件设计提供新的可能.另外,如果考虑磁性范德瓦耳斯材料,只要对称性合适,直流门电场不仅可以引起面外磁化,还可以引起面内磁化,从而有可能改变系统的磁有序状态.此外,通过转角对谷电子的独特影响可以在长周期莫尔纹中引入来自实空间层赝自旋结构的量子几何特性,比如实空间的贝里曲率等效实现的莫尔赝磁场[27]为转角双层二维半导体中量子反常霍尔效应的出现提供了要素.

上面评述和展望的量子层电子学效应主要讨论双层体系中电子层自由度和面内轨道自由度耦合的量子几何性质和物理效应.实际上范德瓦耳斯材料里电子的层自由度和其他内部自由度,比如自旋自由度和能谷自由度,也存在丰富的耦合[29],会产生更多新颖的量子几何效应.多层体系中电子层自由度不再是一个二维的自由度,而具有随层数增加而愈加丰富的内部结构,完全超出自旋-赝自旋类比的范畴,可以预期会引起双层体系没有的新现象.量子层电子学的进一步发展会揭示出,即使是范德瓦耳斯体系独有的性质,也极其丰富.探究它们在功能器件设计上的潜力将对范德瓦耳斯材料的应用前景产生积极影响.