哈勃常数危机*

蔡荣根 李理 王少江

1)(宁波大学物理科学与技术学院,宁波 315211)

2)(中国科学院理论物理研究所,北京 100190)

3)(中国科学院大学物理科学学院,北京 100049)

4)(中国科学院大学杭州高等研究院,杭州 310024)

1 引言

哈勃常数初见于 1929年美国天文学家 Edwin Hubble 对近邻星系的退行速度的估测中.他大胆猜测近邻星系的退行速度vr与其光度距离DL成正比,即vr=H0DL,其中比例系数H0≡100hkm/(s·Mpc)被后世称为哈勃常数,h是一个无量纲的常数.哈勃的发现预示着宇宙处在膨胀中.事实上,早在哈勃发现的两年前,比利时天文学家Georges Lemaître 也曾撰文表达了类似的想法.Hubble-Lemaître 定律是宇宙膨胀的第一个观测证据,它直接促使爱因斯坦放弃了引入宇宙学常数来得到静态宇宙的执念.我们现在知道,H0是当今宇宙膨胀的尺度因子的时间导数与该尺度因子的比,它衡量了当前宇宙膨胀速率的大小.但受限于当时的观测技术水平,对H0的最初估计(H0=500 km/(s·Mpc))非常粗糙.经过将近一百年的发展,目前对H0的测量精度已经达到1%.然而,最近不同测量方法测得的哈勃常数值之间却出现了难以弥合的裂痕.这其中最为突出的冲突来自早期宇宙和晚期宇宙的两种测量方法: 一种是借助来自于早期宇宙再复合时期光子退耦从最后散射面传播到现在的宇宙微波背景辐射数据对宇宙学标准模型的全局拟合得到的观测限制,另一种是借助局域距离阶梯测距手段对经由造父变星校准后哈勃流上的Ia 型超新星观测得到的直接测量结果.对于前者,Planck 卫星合作组在2018年对哈勃常数的全局拟合值为H0=(67.27±0.60)km/(s·Mpc)[1];对于后者,由诺贝尔物理学奖获得者Adam Reiss领导的 SH0ES (supernovaH0for the equation of state)合作组在 2022年对哈勃常数的直接测量值为H0=(73.04±1.04)km/(s·Mpc)[2].易见它们之间出现了高达接近5 个标准差置信度的偏离(见图1).如果该偏差不能用这两种测量手段各自的观测和/或系统误差解释,那么这毫无疑问地对当前宇宙学标准模型提出了严峻挑战.此即哈勃常数危机[3–14],其获解可能需要超出当前宇宙学标准模型的新物理.

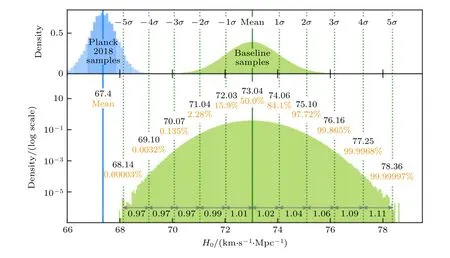
图1 哈勃常数危机: 来自 CMB-Planck+ΛCDM 的 H0 限制(蓝色)与来自 SH0ES 合作组距离阶梯 SNe+Cepheid 的 H0 测量(绿色)之间高达将近 5σ 的偏离.图片来自文献[2]Fig.1.The Hubble-constant tension: The nearly 5σ discrepancy between the H0 constraint (blue)from CMB-Planck+ΛCDM and the H0 measurement (green)from SH0ES group using the distance ladder SNe+Cepheid.The figure comes from Ref.[2].

本文安排如下: 第2 节简介各种观测结果,其中第2.1 节简介来自早期宇宙的观测结果(包括与宇宙微波背景辐射相关和无关的测量),第2.2 节简介来自晚期宇宙的观测结果(包括与局域距离阶梯测距相关和无关的测量);第3 节简介各种模型构造,其中第3.1 节简介对早期宇宙的模型构造(包括修改再复合历史和早期膨胀历史),第3.2 节简介对晚期宇宙的模型构造(包括对晚期宇宙的均匀性修改和非均匀性修改);第4 节结合作者近年来的研究工作对哈勃常数问题进行展望,其中第4.1 节从观测角度展望(包括局域和非局域的宇宙学方差),第4.2 节从理论角度展望(包括变色龙暗能量和对尺度依赖的暗能量的讨论);第5 节总结全文.

2 观 测

哈勃常数危机在观测方面不仅体现为 Planck合作组与 SH0ES 合作组对哈勃常数值高达接近5σ的偏离,还体现在借助晚期宇宙直接测量的哈勃常数值系统性地低于借助早期宇宙全局拟合的哈勃常数值(见图2).

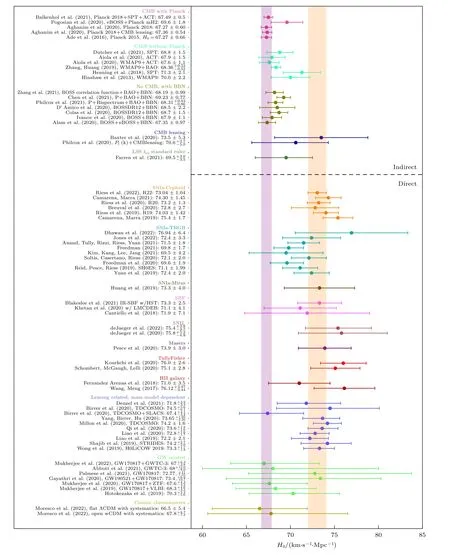
图2 哈勃常数危机: 来自早期宇宙的间接拟合和晚期宇宙的直接测量.图片来自文献[8]Fig.2.The Hubble-constant tension: The indirect constraints from fitting the early Universe and direct measurements from the late Universe.The figure comes from Ref.[8].

2.1 早期宇宙

虽然对早期宇宙的观测是在当前这个晚期宇宙进行的,但是所获得的数据实际上反映的是早期宇宙的信息.然而这些信息不能直接用来测量当前宇宙的哈勃膨胀率(即哈勃常数),因此需要借助特定的宇宙学模型将早期宇宙的信息外延映射到晚期宇宙.这样得到的哈勃常数值通常被称为给定数据情况下对模型参数的全局拟合值.

2.1.1 宇宙微波背景辐射

在目前已知的粒子物理标准模型结合宇宙学标准模型框架下得到观测证实的历史中,早期宇宙诞生1 s 即中微子开始退耦不久,正负电子湮灭就开始了,3 min 后随着宇宙逐渐冷却开始合成轻元素此即原初核合成(BBN: big bang nucleosynthesis).6 万年后宇宙中辐射和物质的量大致相当,其后电子和质子合成氢并放出光子的逆过程开始难以弥补正过程所损失的电子,导致电子和光子的Thomson 散射过程在宇宙年龄达到38 万年时难以维持,从而导致光子从背景等离子流体中脱耦出来,开始自由流动(free streaming)形成最后散射面,此即宇宙微波背景辐射(CMBR: cosmic microwave background radiation).此后,这些 CMB光子穿行过物质结构的引力势阱,最后,其中的一部分 CMB 光子到达地球附近并被我们观测到.

利用 CMB 数据测量哈勃常数值的过程是一个全局拟合的统计分析,但是我们依然可以近似解析地理解这个过程.CMB 数据记录的是各个方向到达我们的 CMB 光子的温度T(nˆ),理论预言该温度谱是一个黑体辐射谱,从而可以拟合一个各向同性的背景温度T0=(2.7255±0.0006)K,从而得到该方向上的温度涨落Θ(nˆ)≡δT(nˆ)/T0.实测的CMB 温度涨落标准差仅有万分之一大小,这个观测事实导致了所谓极早期宇宙存在一段近指数膨胀的暴胀时期,该时期微观量子扰动被快速拉出哈勃视界退化为经典扰动,暴胀结束后哈勃视界重新开始增大,并在其后不同时刻接纳不同尺度的经典扰动重新进入视界,诱导重子-光子流体的扰动并传递到最后散射面上,成为脱耦光子的温度涨落.通常假设宇宙暴胀时期产生的原初量子扰动是一个近尺度不变的绝热演化的高斯随机标量场,因此其功率谱被唯象地参数化为PR(k)=As(k/kref)ns-1,这里As是振幅,ns是标量谱指标,kref是某个观测参考尺度.

即为测到的角功率谱.该角功率谱一个十分明显的特征是它的各个声学振荡峰,其中对第一个声学峰

的位置测量十分精准,这里最后散射面的红移z∗可以由忽略再电离过程的 Thomson 散射光深τ达到 1 时所定义,而我们现在相对最后散射面的角直径距离DA(z∗)主要由晚期宇宙的膨胀历史E(z)2≡=ΩΛ+Ωm(1+z)3+Ωr(1+z)4所 决定,但是最后散射面上的声学视界rs(z∗)则由再复合历史决定的z∗以及早期膨胀历史决定的哈勃参数H(z)和声速共同决定,其中重光比来自物理的重子丰度ωb≡Ωbh2以及物理的光子丰度ωγ≡Ωγh2=2.473×10-5(T0/ 2.7255).

宇宙学标准模型通常选取θ∗,τ,ωb,ωc,As和ns作为全局拟合的基本参数(注意哈勃常数是它们的导出参数),当这6 个参数被数据确定后,可以通过 CMB 角功率谱的第一个声学峰位置θ∗反解出ωΛ≡ΩΛh2,最后取宇宙学标准模型,即 ΛCDM (Λ-cold-dark-matter)模型的 Friedmann 方程

在z=0 时的值,即可得到 CMB+ΛCDM 所限制的哈勃常数值,其中物理的辐射丰度ωr≡Ωrh2是一个分段函数,在正负电子湮灭前为ωr=(g/2)(4/11)4/3ωγ,在正负电子湮灭后为ωr=[1+(7/8)(4/11)4/3Neff]ωγ,这里有效相对论性自由度数目的演化g由粒子物理标准模型给出,同时它在假设最小质量正序中微子情况下还确定了类中微子相对论性有效自由度数目Neffe=3.046 .至此给出了利用 CMB 数据对 ΛCDM 全局拟合H0的近似图像.

WMAP (Wilkinson microwave anisotropy probe)9年数据测得H0=(70.0±2.2)km/(s·Mpc)[15],该结果比Planck 组2018年的结果[1]H0=(67.27±0.60)km/(s·Mpc)更大,但其他与 Planck 实验组无关的地面观测也给出了和 Planck 实验组类似的结果,如 SPT (south pole telescope)-3G 测得H0=(68.8±1.5)km/(s·Mpc)[16],而 ACT (atacama cosmology telescope)测得H0=(67.9±1.5)km/(s·Mpc)[17].

2.1.2 重子声学振荡+原初核合成

Planck 组2018年给出的哈勃常数明显小于它的前任卫星 WMAP9 所给出的哈勃常数,这一度引起了对 CMB 数据质量与分析方法的担忧,但是当 WMAP9 与重子声学振荡(BAO: baryon acoustic oscillation)结合时给出了与 Planck 组类似 的[20].实际上,完全独立于CMB 观测,BAO 与BBN 联合限制哈勃常数已经可以得到与 Planck 组类似的哈勃常数值[19](图3 所示),比如H0=(67.35±0.97)km/(s·Mpc)[21],H0=(67.9±1.1)km/(s·Mpc)[22],H0=(68.6±1.1)km/(s·Mpc)[23]及H0=(68.19±0.99)km/(s·Mpc)[24]等.下面分别介绍BAO 和BBN观测以及它们的联合限制可以用来测量哈勃常数的基本物理图像.

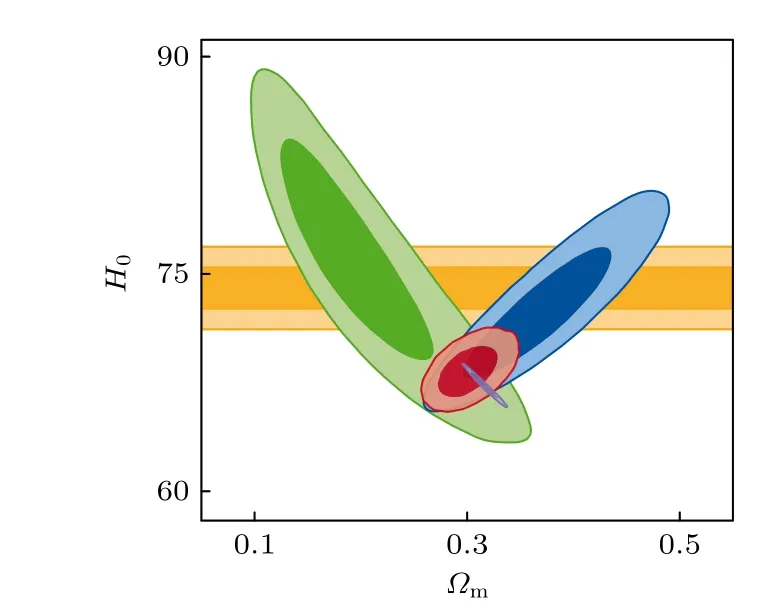
图3 把BBN 与星系BAO(蓝色)和Lyman-α BAO(绿色)结合后给出的限制(红色)与Planck 2018 限制结果(紫色)和SH0ES 组测量结果(橙色)的对比.图片来自文献[18]Fig.3.The comparison to the Planck 2018 constraint(purple)and the SH0ES measurement (orange)with respect to the joint constraint (red)from combing BBN with galaxy BAO (blue)and Lyman-α BAO (green).The figure comes from Ref.[18].

BAO 观测来自大尺度结构星系巡天,它所记录的数据是星系的红移(通过某个给定基准模型转化为距离)和方位角以及其他测光或者光谱数据,从而在给定基准模型下确定各个星系的位置.星系的位置排布并不是完全随机的,这是因为原初扰动进视界后诱导重子-光子流体的密度扰动,该密度扰动在空间各点以声速向外传播开来,但是当光子从重子-光子流体中脱耦出来后,原来的重子物质部分无法维系该声学振荡的继续传播,因此该密度扰动被冻结下来,其共动尺度大约为rs≈150 Mpc.之后,重子物质落入暗物质所形成的引力势阱中形成星系,这些星系位置的两点关联函数在rs处相比于完全随机分布的情形就有了一个局部的超出.因此,虽然 BAO 数据来自于对晚期宇宙星系分布的观测,但是它所记录的信息直接来自于早期宇宙在最后散射面(或者更准确地说是重子拖拽时期)上所留下的声学视界信息.但是,BAO 并不能直接测量该声学视界,而是分别在平行视线和垂直视线方向测量其与基准模型所预言的以下组合量的偏离:

其中两个参数

才是BAO 观测中两点关联函数(或者其傅里叶空间对应即功率谱)所直接测量的物理量.特别地,BAO 功率谱限制给出乘积rsH0≈const.近似为一个常数,因此从修改早期宇宙的模型构造角度出发,期待一个更大的哈勃常数通常意味着一个更小的声学视界.

BBN 观测来自于对宇宙中各种轻元素的丰度测量,比如原初氦丰度=4nHe/nb和原初氘丰度yDP=105nD/nH,它们都是物理的重子密度ωb和相对论性的类中微子的有效自由度数目Neff的函数,具体的函数关系可以由公开的 BBN 代码PArthENoPE[25]和PRIMAT[26]根据粒子物理标准模型(加上中微子扩展)给出.换言之,对于给定的粒子物理模型,仅仅知道Neff与ωb之间的关系,而观测到的和yDP又 在Neff-ωb平面上相交出一块置信度区域,该区域与模型给定的Neff-ωb函数关系的重合区域确定了Neff和ωb各自的置信度区间,由此确定了声速中的重光比,因此当与 BAO功率谱确定的第一个声学峰限制结合时,可以得到对H0-Ωm的联合限制.当 BBN 与不同的BAO 观测结合时,该联合限制通常足以对哈勃常数给出很强的限制.

2.2 晚期宇宙

与前述早期宇宙观测不同,对晚期宇宙的观测似乎可以直接测量当前宇宙的哈勃膨胀率,即哈勃常数本身.但是由于晚期宇宙的物质扰动增长经历了一段非线性演化时期,因此对局域宇宙的测量本身会受到诸多系统误差的影响,从而难以提取出晚期局域宇宙中真正来自全局背景膨胀部分的贡献.

2.2.1 距离阶梯测距

晚期局域宇宙测量哈勃常数的关键在于通过测距来测量距离-红移关系:

其中E(z)≡H(z)/H0依赖于具体的宇宙学模型参数输入.但是不同的测距手段的适用范围不同,因此需要将不同测距手段联结起来形成距离阶梯.最低一级的距离阶梯是利用一些几何测距方法(如三角视差、脉泽、不接食双星方法等)来定标某些中等距离上的光度距离指示器(如造父变星、红巨星支顶端、面亮度起伏、Miras 等);在第二级距离阶梯上,这些中等距离上的光度距离指示器可以作为校准器用来进一步定标一些更远的光度距离指示器(如 Ia 型超新星、II 型超新星、HII 星系等);最终在第三级距离阶梯上,这些经过定标的远距离光度距离指示器可以用来测量局域宇宙哈勃流上的哈勃常数,其中观测品质最好的远距离光度距离指示器是作为标准烛光的 Ia 型超新星.SH0ES 合作组所采用的三级距离阶梯示意图见图4.

图4 SH0ES 合作组采用的三级距离阶梯.图片来自文献[2]Fig.4.The three-rung distance ladder adopted by the SH0ES group.The figure comes from Ref.[2].

Ia 型超新星之所以可以作为标准烛光,是因为它来自于双星系统中碳氧白矮星由于吸积其伴星(如主序星、亚巨星、红巨星或者氦星等)的物质,直到达到钱德拉塞卡极限(1.44 个太阳质量),从而达到点火温度重启碳聚变,进而诱发白矮星爆炸所产生的遗迹,因此其光变曲线达到最大时的绝对光度几乎是相等的(记为M).根据距离模数µ≡m-M的定义,Ia 型超新星的视光度为

其中〈c〉是光速以 km/s 为单位的纯数值部分,而〈H0〉≡100h是哈勃常数H0以 km/(s·Mpc)为单位的纯数值部分.因此,一旦通过第一、二级距离阶梯确定了 Ia 型超新星的绝对光度M,那么根据测量到的多个 Ia 型超新星的视光度mi,就可以联立限制给定模型E(z)中的参数.为了能够模型无关地测量哈勃常数,可以选取哈勃流上特定红移范围内的 Ia 型超新星,使得光度距离按低红移展开,dL(z)=z[1+(1/2)(1-q0)z+···]中的第二项(宇宙学标准模型下减速参数q0≈-0.5)远小于第一项,(1/2)(1-q0)z≲0.1,从而得到哈勃流的红移上限z≲0.13 (哈勃流的红移下限z≳0.023,见第4.1 节).

事实上,只要 Ia 型超新星绝对光度如SH0ES组所测量的那样在M=-19.2 左右,那么大部分晚期宇宙模型所测得的哈勃常数就都在73—74 km/(s·Mpc)左右[27].因此,真正造成晚期局域测量哈勃常数值差别的是对Ia 型超新星绝对光度的定标,如利用造父变星/红巨星支顶端/面亮度起伏/Miras 等校准器定标的Ia 型超新星所测得的哈勃常数分别为

正因如此,哈勃冲突(H0tension)有时也被称为MBtension.

2.2.2 距离阶梯无关测距

由于多级距离阶梯的构造要求相邻两级距离阶梯的两种光度距离指示器在锚定星系上进行校准和定标,不可避免地导致每级距离阶梯的校准定标误差层层传递,从而在最后一级距离阶梯引入十分可观的观测和系统误差.虽然在过去的二十多年里,SH0ES 实验组通过非凡的努力将距离阶梯的各级校准误差的总和降低到 1% 以下,但是如果能有一种方法避免构造距离阶梯,实现远距离直接测距,那么将显著降低对晚期局域宇宙测量哈勃常数的观测和系统误差,比如脉泽、面亮度起伏、Tully-Fisher 关系、强引力透镜时间延迟和引力波标准汽笛等方法.

强引力透镜时间延迟是通过对强引力透镜系统测量其不同透镜像到达我们的时间差来测量哈勃常数.通常强引力透镜系统的透镜源(背景天体)是类星体甚至是超新星,而透镜体(前景天体)是星系.当透镜源的光线经过透镜体时,由于引力势阱的光线偏折效应,使得当回溯这些到达我们的光线时,会发现对应于该透镜源的多重成像.这些多重像在大多数情况下呈现非对称的排布,因此不同光路因路程不同而耗时也不同(称为几何时间延迟),而且广义相对论效应还引入了因为光线等效传播速度的变化而造成的 Shapiro 时间延迟,因此最后总的时间延迟为,其中时间延迟距离

依赖于观测者到透镜体和透镜源的角直径距离以及透镜体到透镜源的角直径距离,而透镜星系的费马势 ∆ϕ则来自于对星系质量径向分布函数的估计.最初,质量径向分布函数被简单地假设为幂律形式,由此 H0LiCOW (H0Lenses in COSMOGRAIL’s Wellspring)组测得km/(s·Mpc)[31],而DES (dark energy survey)组则测得H0=km/(s·Mpc)[32].但是当 TDCOSMO (timedelay cosmography)组采用SLACS (sloan lens advanced camera for surveys)星系样本(不过没有强引力透镜现象)来实际推算透镜星系质量径向分布函数时,由此得到的哈勃常数值降至km/(s·Mpc)[18],如图5 所示.

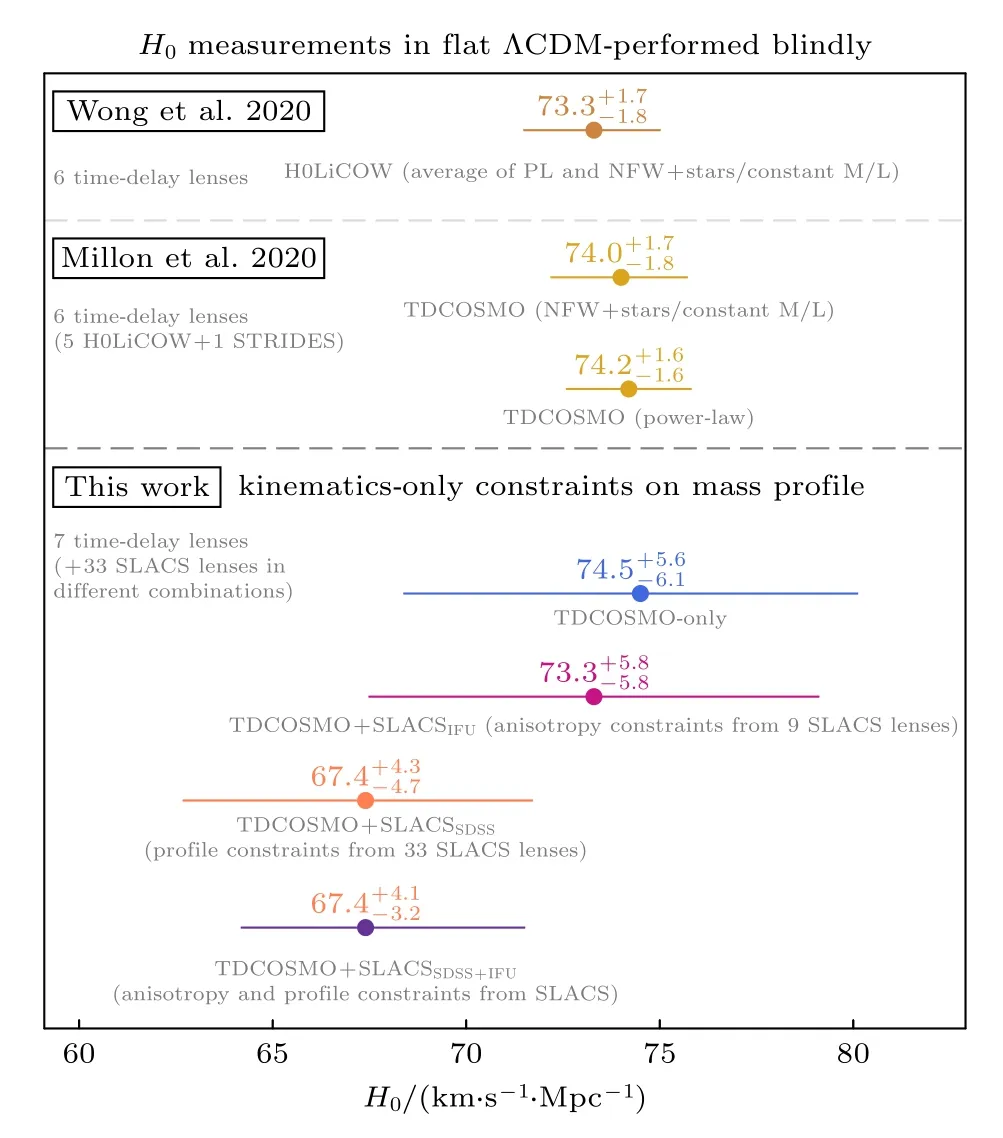
图5 来自与距离阶梯无关的强引力透镜时间延迟对哈勃常数测量,图片来自文献[18]Fig.5.The Hubble-constant measurements from strong lensing time delay independent of distance ladders.The figure comes from Ref.[18].

引力波标准汽笛利用致密双星系统的旋进(inspiral)阶段辐射的引力波波形

来实现远距离直接测距[33–35],其DL(z)是光度距离,Mc(z)是红移后的啁啾(chirp)质量,ι是双星系统轨道平面相对我们视线方向的倾角,Φ(f)是相位.将测得的旋进阶段的引力波信号与上述波形做模板匹配,可以直接测得光度距离DL.如果该引力波波源系统同时还拥有电磁对应体(比如双星中有一个是中子星),且其发射的电磁波信号能够被我们观测到(即双星系统的轨道倾角小于20°),就可知其红移z,那么由Hubble-Lemaître定律cz=H0DL可以直接测得哈勃常数值H0.比如对双中子星并合事件 GW170817[36]测量得到的哈勃常数值为km/(s·Mpc)[37],[38]以及km/(s·Mpc)[39].如果该引力波事件没有对应的电磁波信号,那么需要多台引力波探测器联网定位该引力波事件的方位.如果在该方位上正好有已知的宿主星系的红移信息,那么也可由此测得哈勃常数值.比如将美欧航空局的 LISA 空间引力波探测器与中国的太极引力波探测器联网[40],可以借助上述暗汽笛的方法,利用5年的联网观测,有望将哈勃参数的限制精度提升到 1% 以内(见图6).

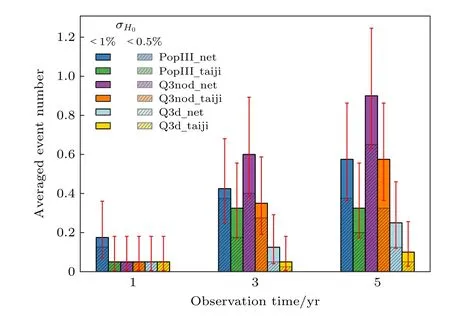
图6 来自 LISA 和太极空间引力波探测器联网的对哈勃常数的暗汽笛限制.图片来自文献[40]Fig.6.The dark siren constraints on the Hubble constant from the LISA-Taiji network.The figure comes from Ref.[40].

3 模 型

尽管来自早期和晚期宇宙的观测对哈勃常数的限制不尽相同,但是有一种趋势不可忽视,那就是晚期宇宙对哈勃常数的直接测量值系统性地高于来自早期宇宙的全局拟合值.由于各种观测手段的观测和系统误差不尽相同,很难想象有某种共通的观测和系统误差导致了这种系统性的偏离.第4.1 节将讨论这种可能性,本节将预设这种系统性的偏离来自于某种新物理模型.

最简单的新物理模型构造来自于对宇宙学标准模型简单而直接的扩展,比如引入微小的空间曲率,在晚期宇宙引入CPL (Chevallier-Polarski-Lin)参数化的动力学暗能量,在 BBN 之前引入微小的新的类中微子的相对论性自由度,以及上述扩展的排列组合等扩展.但已经有众多研究(如文献[41,42])表明,对宇宙学标准模型的简单扩展仅仅只是增大模型参数的不确定性,但不足以完全解决哈勃常数危机问题.

因此,需要对宇宙学标准模型进行某种高度特异性的修改,比如引入新的能量密度组分、新的相互作用形式、新的修改引力效应等,甚至不惜修改基本物理常数随时间的演化,乃至动摇宇宙学基本原理等尝试.由于哈勃常数危机可以被粗略地认为是来自于当前对早期宇宙与晚期宇宙的观测之间的矛盾,因此其模型构造也可以粗略地分为对早期宇宙演化的修改和对晚期宇宙演化的修改.

3.1 早期宇宙

对早期宇宙的修改需要至少符合现有CMB和BAO 的限制,而CMB 和BAO 本质上测量的主要是声学视界的角尺度大小θ∗,它是声学视界留在最后散射面上的大小rs(z∗)与最后散射面到我们现在的角直径距离DA(z∗)之比.一方面,由于DA(z∗)反比于H0,因此为了增大H0,在不改变角尺度θ∗大小的情况下,需要减小声学视界rs(z∗)的大小.另一方面,在保持BAO 关系rsH0=const.不变的情况下,为了增大H0,也需要减小声学视界的大小.减小声学视界的办法有两种: 一种是减小声波传播的时间,另一种是直接减小声速本身.减小声波传播的时间可以通过修改光子脱耦过程中的再复合历史,进而使得再复合时期提前,从而减小声学视界;而减小声速可以通过修改光子脱耦前的膨胀历史,进而修改重光比中辐射和(重子)物质的相对大小.

3.1.1 修改再复合历史

修改再复合历史可以通过加入原初磁场[43]或者允许非标准的再复合历史[44]来实现.以原初磁场为例,当前的天文学和宇宙学观测(比如星系、星系团和空洞等)经常遇到磁场环境[45],它的起源目前仍然是一个迷,但是一般认为它可能产生自早期宇宙(比如电弱相变或者暴胀等).这样的原初磁场会诱导产生小尺度的非均匀性,迫使重子沿着磁场转移到磁场能量密度更低的区域,从而加快再复合进程进而减小声学视界并抬高哈勃常数.然而,从CMB 数据中并没有发现重子在小尺度上结成团块的证据[46,47],因此原初磁场方案并不能解决哈勃常数问题.类似地,CMB 数据同样不支持非标准的再复合历史[48],除非某种特异性的新物理改变了原子物理常数(如氢原子电离能)或者基本物理常数(如电子质量)在早期宇宙的演化[49,50].

3.1.2 修改早期膨胀历史

修改早期膨胀历史可以通过向早期宇宙中注入新的能量组分实现,比如暗辐射和早期暗能量.先来看暗辐射: 由于BBN 已经强烈地限制了BBN之前的类中微子的相对论性的有效自由度数目,因此必须在BBN 之后才能引入暗辐射,从而不破坏BBN 对之前的有效自由度数目限制.如果引入的暗辐射是类似光子那种可以自由流动(free streaming)的辐射组分,那么它将冲刷掉小尺度的辐射扰动,从而改变CMB 功率谱在小尺度上的Silk 衰减尺度(Silk damping scale).事实上,引入自由流动的暗辐射是无法同时保持声学峰和Silk 衰减尺度都不变的.因此只能引入不能自由流动的暗辐射,比如具有强烈自相互作用的中微子[51],但是这样又会导致CMB 极化特征与CMB 数据并不相符[52].

而早期暗能量本质上也是一种暗辐射: 最简单的例子是轴子场[53].调节轴子势函数的形状,使得轴子质量远小于当时的哈勃参数,因此该轴子场将受到背景哈勃阻力的作用,使其在CMB 之前的大部分时间都冻结在势函数的某个位置,作为有效宇宙学常数即为早期暗能量.随着宇宙膨胀,当哈勃参数下降到与轴子质量可以比拟时,轴子就会从自身的势函数上滚下来开始振荡衰减.通过选取合适的势函数形状,可以使得该振荡对应的能量密度衰减速度与辐射衰减速度相当甚至还要更快[54],从而反过来允许我们从一开始就设置更大的早期暗能量初值,进而大幅度改变早期膨胀历史.对该模型的数据分析表明,早期暗能量需要在稍早于辐射物质相等时期,就达到当时总能量的大约5%,然后以比辐射更快的方式衰减掉.

然而这样一个简单的模型,存在着3 个致命的问题: 其一,微调问题,为了使早期暗能量在稍早于辐射物质相等时期达到5% 这个比例,必须小心地微调轴子场的初始值;其二,巧合问题,早期暗能量的积累和快速衰减接替发生的时刻必须稍早于辐射物质相等时期;其三,S8问题,由于引入了早期暗能量抑制了早期物质扰动的增长,因此必须同时增大物质的量以抵消该效应.但是增大的物质的量将在晚期增大最小线性尺度上的物质扰动(即S8),从而与晚期大尺度结构巡天对物质扰动的限制不相符.事实上,上述问题三的讨论也适用于几乎所有修改早期宇宙的模型[12],它们要么与星系成团的观测性质不相符,要么与星系弱引力透镜的限制不符(见图7).

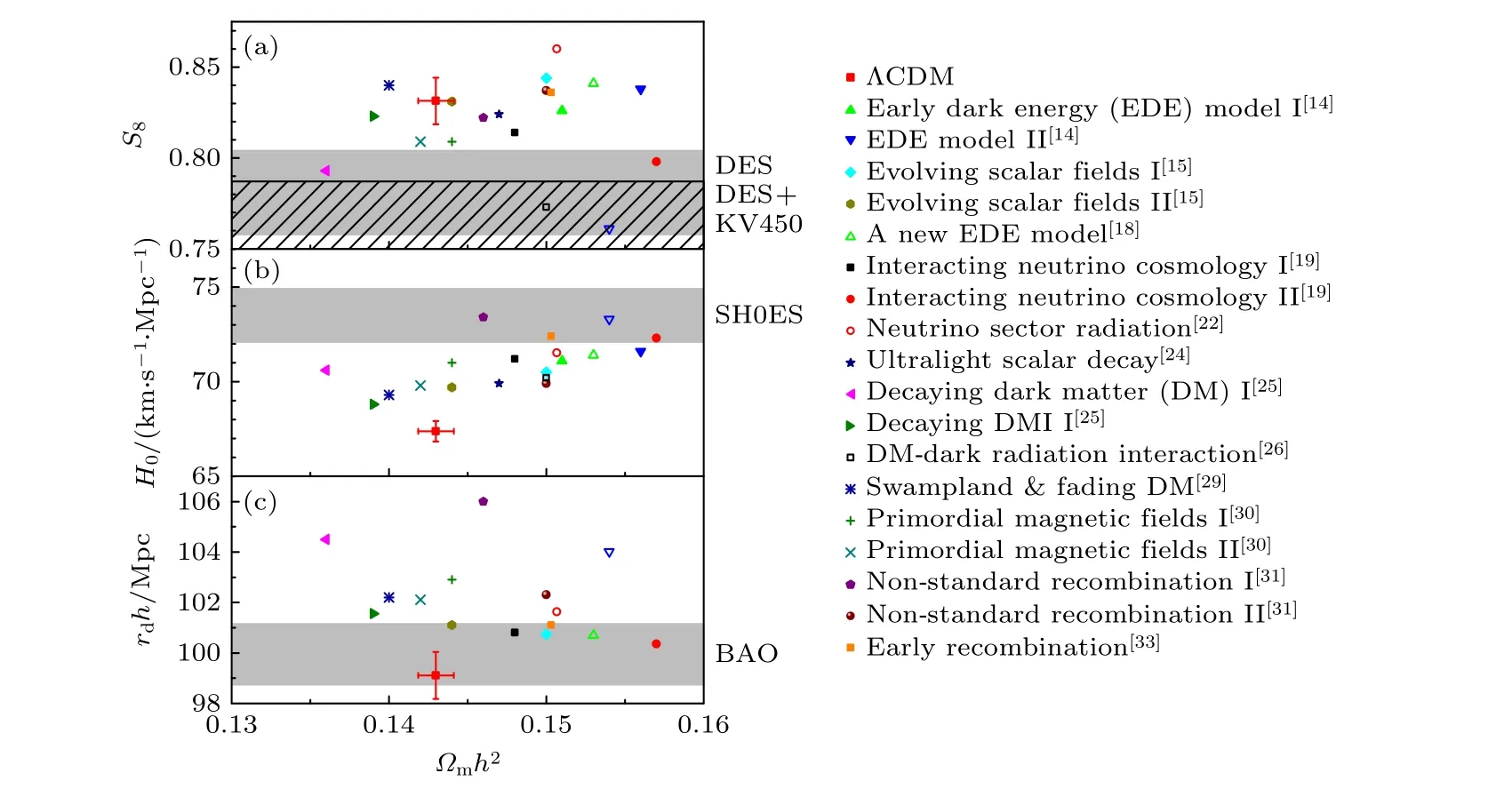
图7 星系弱引力透镜观测(左上)、SH0ES 组对 H0 的测量(左中)以及重子声学振荡观测(左下)对早期宇宙模型(右)的限制.图片来自文献[12]Fig.7.The constraints (left)on the early-Universe models (right)from the galactic weak lensing observation (left top),the SH0ES measurement on H0 (left medium),and the BAO observation (left bottom).The figure comes from Ref.[12].

3.2 晚期宇宙

对晚期宇宙的修改可以大致分为均匀性修改和非均匀性修改两类,取决于修改晚期宇宙的新物理模型是否具有空间依赖性.

3.2.1 均匀性修改

如果修改晚期宇宙的新物理模型仅具有时间依赖性,则属于均匀性修改,比如大多数的动力学暗能量模型.但是,几乎所有对晚期宇宙的均匀性修改模型都会受到反向距离阶梯的强烈限制.不同于正常的距离阶梯(比如被造父变星定标的 Ia 型超新星),反向距离阶梯[55–57]利用哈勃流上未定标的 Ia 型超新星与BAO 数据联合形成从低红移(z≈0.1)到高红移(z≈1)的反向距离阶梯,并在高红移处定标(通常由CMB 观测在宇宙学标准模型限制下的声学视界作为先验定标BAO[58–60]).正是由于反向距离阶梯仅需要来自早期宇宙的声学视界定标,因此它并不依赖于晚期宇宙模型,从而可以对晚期宇宙模型给出模型无关的限制,并且这些反向距离阶梯限制给出的哈勃常数值偏向来自于早期宇宙的测量结果[21,61–65],除非改变早期宇宙模型给出的声学视界先验,进而反过来佐证模型修改应该来自早期宇宙.即使将反向距离阶梯的高红移定标从CMB 观测给出的声学视界替换为其他高红移观测,如强引力透镜时间延迟观测[66,67]和引力波标准汽笛[68],所得到的哈勃常数限制依然偏向来自早期宇宙的测量结果.因此,对晚期宇宙的均匀性修改模型也似乎无法完全解决哈勃常数问题.

一种可能逃脱反向距离阶梯限制的模型构造来自于对极晚期宇宙的修改,这里极晚期宇宙是指它相对于宇宙学标准模型的偏离发生在哈勃流红移下限之内(即z≲0.01),比如发生在极晚期的幽灵暗能量转变(phantom dark energy transition)模型,其暗能量的状态方程参数在极晚期穿越幽灵转变点w=-1[69].由于这种幽灵暗能量模型在哈勃流上限红移之上和宇宙学标准模型一致,因此它并不会破坏早期宇宙观测限制甚至反向距离阶梯限制.但是,当把正向距离阶梯和反向距离阶梯结合起来的时候,就会发现这个模型的内部不自洽性[27,70–72].具体来说,利用未定标的Ia 型超新星作为正向距离阶梯限制出来的哈勃常数H0和超新星绝对光度M与被CMB 定标的反向距离阶梯限制出来的H0和M均存在冲突,即使将反向距离阶梯限制的M用来定标正向距离阶梯中的 Ia 型超新星得到的H0,与正向距离阶梯限制的H0也还是存在冲突.因此无论对晚期宇宙进行何种整体均匀性修改,哈勃常数危机依然存在.

在最近的两篇工作[13,14]中我们通过改良传统的反向距离阶梯进一步强化了这个结论.传统的反向距离阶梯需要一个位于高红移的定标物,通常是CMB 在给定早期宇宙模型下的声学视界,从而得到与晚期宇宙模型无关的限制,但是它也显然依赖于早期宇宙模型.我们选取宇宙学年龄即宇宙学标准时钟(CC: cosmic chronometer)测量[73]作为高红移定标物,它通过对一类缓慢演化的星系的年龄-红移关系的持续追踪直接测量高红移的哈勃膨胀率,

因此避开了传统测距手段中对宇宙学模型H(z)的积分,从而与任何宇宙学模型都无关.为了契合宇宙学标准时钟数据的使用,我们进一步采用了一种基于宇宙学年龄的参数化方法 PAge (parametrization based on the cosmic age)模型[74–76].该模型基于宇宙年龄主要来自于物质主导时期的事实,将Ht展开到t的二阶得到

其中两个自由参数page=H0t0和η表征了当暗能量开始主导宇宙膨胀时宇宙年龄对物质主导时期宇宙年龄关系Ht=2/3 的偏离,这里忽略了辐射主导时期对宇宙年龄的微小贡献.PAge 模型优于其他模型参数化方法的地方在于它是一种经济且全局的参数化,它只用两个参数就非常精确而忠实地表达了各种晚期模型在全部红移范围内的演化行为,而其他参数化方法(如按红移z或者y=1-a的泰勒展开)在中高红移(如z≈1)端就已经严重偏离了它所参数化的宇宙学模型(见图8).借助该改良版的反向距离阶梯[13,14],我们发现有很强的证据(BIC 判据大于10)表明PAge 模型所参数化的新物理模型并不优于宇宙学标准模型ΛCDM模型,即对晚期宇宙的均匀性修改模型并不比ΛCDM 模型更能解决哈勃常数危机.

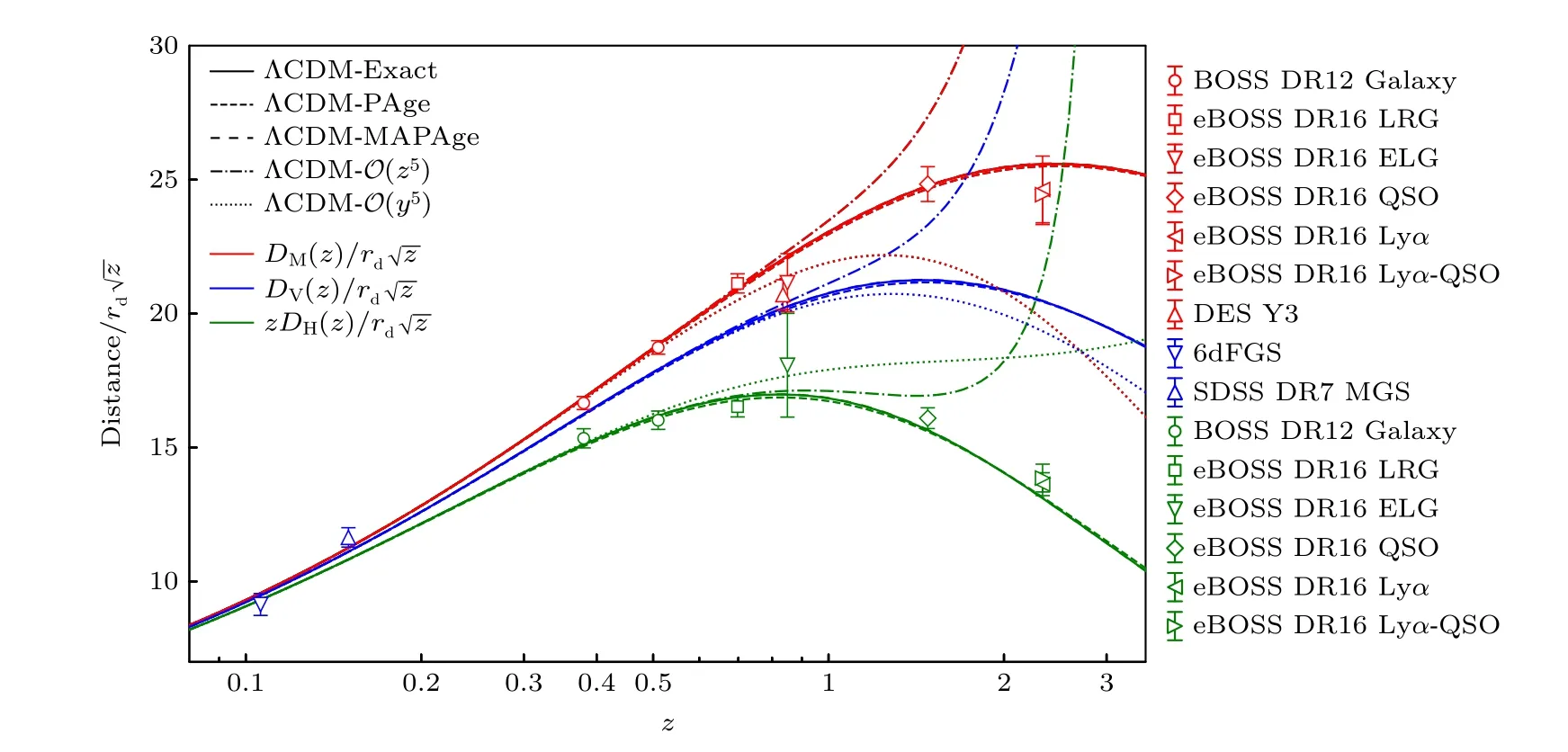
图8 在 ΛCDM 模型及其PAge/MAPAge 参数化模型以及按红移 z和y=1-a 的泰勒展开近似下的BAO 特征尺度(红、蓝、绿)与BAO 观测数据的对比.图片来自文献[14]Fig.8.The comparison of characteristic BAO length scales to the BAO data from the ΛCDM model and its PAge/MAPAge parameterization models as well as its Taylor expansion models in redshift z and y=1-a .The figure comes from Ref.[14].

3.2.2 非均匀性修改

如果修改晚期宇宙的新物理模型还具有对空间的依赖性,则属于非均匀性修改,比如相互作用暗能量模型[77].该模型引入暗能量与暗物质之间的相互作用,使得一部分暗物质可以衰变为暗能量.由于暗物质本身具有空间涨落,因而与之相互作用的暗能量也产生了对空间的依赖性.相互作用暗能量模型增大了晚期暗能量的比重,进而直接推高哈勃膨胀速率;而暗物质本身的减小又以增大哈勃常数为代价才能保持物理的暗物质能量密度比例ωcdm=Ωcdmh2与CMB 限制相符;另一方面,允许一部分暗物质衰变为暗能量还同时减小了晚期物质结构增长,从而缓解了S8问题.此外,作为对晚期宇宙的非均匀性修改,它可以不受前述反向距离阶梯对晚期均匀性模型的强烈限制.因此,从各方面来说,相互作用暗能量模型是一个解决哈勃常数危机的潜在候选者[78].

另一种对晚期宇宙的非均匀性修改来自于对晚期宇宙学原理的质疑[79],比如我们处于一个局域的宇宙学大空洞(即cosmic void)中.在这种空洞中星系的分布十分稀疏,因此相比于宇宙的其他区域,空洞中的物质密度比例很低,相应地其暗能量分布就会相对更高,因而局域哈勃膨胀率也更大.值得注意的是,早在20 世纪90年代中期,我国学者就在国际上最早提出过利用局域宇宙空洞解释哈勃常数被高估的问题[80,81].最近的星系巡天观测[82]似乎支持我们处于一个半径为 300 Mpc深度为-30% 的局域宇宙学大空洞(即 KBC: Keenan-Barger-Cowie 空洞[83])中,因此有研究猜测该空洞正是造成哈勃常数危机的原因[84].但是如果用 Ia 型超新星示踪不同红移处的哈勃膨胀率,那么会发现所声称的低密度范围与超出其半径的观测结果不相容[85,86].因此,不存在足够大足够深的局域宇宙学大空洞足以解决哈勃常数问题[87].

4 展 望

至此,分别从观测和模型两方面对哈勃常数问题进行了简要回顾,其中观测方面所展示的早期观测结果系统性地低于晚期观测结果的总体趋势在一定程度上佐证了哈勃常数问题的迫真性,而模型方面所展示的无论早期模型构造还是晚期模型构造都将面临的来自各种观测的强烈限制也展现了解决哈勃常数问题的困难程度.仅以作者有限的认知以及偏颇的观点来看,目前看起来最有希望同时解决H0问题以及S8问题的模型或许是相互作用暗能量模型,但是具体的相互作用形式目前还不得而知,有待未来更为细致的检验和探索.本节将结合作者最近的研究工作介绍一种特殊的相互作用模型[88]及其观测证据[89].

4.1 观 测

来自早期宇宙的观测结果误差较小且分布相对集中,一般认为如果哈勃常数问题的来源果真来自观测和系统误差的话,那么更有可能来自对晚期局域宇宙的测量.然而,来自晚期局域宇宙的测量结果的分布弥散较大,虽然系统性地高于早期观测结果,但是很难用单一的系统误差解释.不过如若能用单一的系统误差解释,那么该系统误差一定存在未被理论模型化的新物理.正因如此,谨慎地检视系统误差仍然十分必要.

关于 Ia 型超新星的距离阶梯测量的误差构成主要分为3 部分: 第一部分来自不同级距离阶梯的校准误差;第二部分来自超新星标准烛光化的误差;第三部分来自超新星样本的宇宙学方差.其中,距离阶梯校准误差目前已降低至 1% 以下,故不再多做讨论.超新星标准烛光化误差来自于这样一个现实,即超新星虽然在理论上是理想的标准烛光,但是在实际观测中却会受到超新星前身星(白矮星吸积模型或者白矮星并合模型等)及其局域环境的各种影响,因此其光变曲线存在一定弥散,需要做各种改正从而变得标准烛光化.

检验标准烛光化的物理量被称为哈勃残差(或距离模数残差),∆µ≡µobs-µmod,其中观测到的距离模数µobs=m-M+αx1-βc+∆bias+∆M,而理论上的距离模数µmod=5 lgdL(z)+5 lg(〈c〉/〈H0〉)+25 在前文已有定义.这里αx1和βc是对光变曲线形状和颜色的改正,∆bias来自模拟,而最值得注意的是来自宿主星系质量的改正∆M.如果不加该质量改正,那么观测到的超新星的哈勃残差呈现出一种特殊的关联性[90–95]: 宿主星系质量越大的超新星,其哈勃残差越负,即µobs相对µmod偏小,也就是说对超新星绝对光度M的等效估计偏大,因此Ia 型超新星内禀光度在更大的宿主星系中看起来更暗,标准烛光化操作需要人为地使它看起来更亮,所以质量改正的形式是一个阶跃函数∆M=γΘ(Mhost-Mstep)-γ/2,其中γ>0,Mstep通常为1010太阳质量.

值得注意的是,根据星系形成理论,更大星系形成于更大的暗物质晕,而更大的暗物质晕更有可能分布于更致密的环境中[96],因此可以大胆猜测Ia 型超新星的哈勃残差也存在与其宿主星系所处物质密度环境的关联.下面在介绍这种关联之前,首先回顾一下借助超新星样本测量哈勃常数时的宇宙学方差与观测者局域密度之间的关联.

4.1.1 局域宇宙学方差

对于哈勃流范围内的超新星,哈勃常数可以通过哈勃定律中距离与退行速度之间的简单关系H0DL=vr=czcos来 估计,其中zcos本应是纯粹背景膨胀引起的红移,需要事先扣除来自超新星本动速度的贡献.但是对超新星本动速度的测量并不总是完整的,因此总会残存一部分本动速度贡献未被考虑.此时测量得到的哈勃常数,除了来自纯粹背景膨胀的贡献,还会掺杂着未被计及的本动速度贡献,因此理论上总是存在一种系统误差,它给出了对特定超新星样本测量得到的哈勃常数对真正来自背景的哈勃常数的偏差.

我们最近的工作[89]在不同超新星样本分布情况下系统计算了这种哈勃偏差δH(observer;sample).特别地,我们还原了一个超局域的超新星样本(即超新星样本无限局域地分布于观测者附近)所得到的哈勃偏差与观测者的局域密度超出δm成负相关的著名结果[97]:

所以,如果一个观测者处于一个局域空洞中,由于其局域密度超出为负,那么该观测者总是会倾向于高估其哈勃常数,这也就是为什么会认为局域空洞可以作为哈勃常数问题的一种解释的原因.但是更进一步的计算表明,对于在观测者周围一定半径范围之间分布的超新星样本,其哈勃偏差的标准差随半径递减[98].因此只需要选取足够远(如哈勃流下限红移z≳0.023 以上)的超新星样本,那么该观测者即使处于一个局域空洞,它对于哈勃常数测量所贡献的哈勃偏差的标准差也可以控制在 1% 以下.所以,一个小于哈勃流红移范围的局域空洞(也被称为哈勃泡泡)并不解决我们所面临的哈勃常数危机(注意这与前述排除宇宙学大小的空洞情况并不一样).

4.1.2 非局域宇宙学方差

对于我们在最近的工作[89]中得到的针对任意样本分布的哈勃偏差,存在一种极为特殊的情况,即如选取的超新星样本的宿主星系都各自处于相同的局域R-尺度平均物质密度超出值,那么该超新星样本对应的哈勃偏差就会与超新星宿主星系的局域R-尺度平均物质密度超出值也呈现负相关关系:

只不过此时比例系数被因子R2/d2所压低,其中d=|rsam-robs|≫R是样本超新星到观测者的距离,尖括号代表对所有这些样本超新星求平均.可以看到,这与4.1.1 节的局域宇宙学方差关系 (12)式不同,这里与哈勃偏差关联的局域密度不再是观测者的局域密度,而是样本超新星宿主星系的局域密度.因此我们将这种关联称为非局域宇宙学方差.

出人意料的是,当利用实际观测数据来直接检验上述非局域宇宙学方差关系时,我们发现观测结果和理论预言也存在不可忽视的冲突.具体来说,利用星系巡天BOSS DR12 (baryon oscillation spectroscopic survey data release 12)数据所重构的物质密度场来估算 Pantheon(+)超新星样本的宿主星系所处的任意R-尺度平均物质密度超出值,然后选取相同局域物质密度的超新星为一组拟合其哈勃常数.研究发现处于越高密度环境下的超新星,其拟合的哈勃常数值也越大.这与非局域宇宙学方差关系所预期的负相关趋势相悖,且相悖的程度在尺度R=60 Mpc/h 时达到将近 3σ的冲突程度.我们称这种冲突为哈勃偏差冲突,它与哈勃冲突和S8冲突都不同,是一种新的宇宙学冲突,它在更深层次上揭示了存在超出当前宇宙学标准模型新物理的可能性.

4.2 模型

既然观测上发现,测量到的哈勃常数总是存在着来自超新星样本的系统误差,且该系统误差还与超新星宿主星系所处的物质密度环境相关联,那么一个自然的问题是该系统误差是否还存在于其他观测中.可以看到,包括超新星观测在内,几乎所有的早期全局背景测量的哈勃常数均系统性地小于晚期局域的测量,这是因为晚期局域宇宙的物质密度增长更大,且各种晚期光度距离指示器都处于这样的高物质密度环境(即星系或者其暗晕)中.

不仅距离指示器,用来校准距离指示器的校准器也呈现这样的规律,比如用红巨星支顶端校准的超新星测量的哈勃常数总是比用造父变星校准的超新星测量结果偏小,这是因为红巨星支顶端通常位于星系盘外低密度的暗晕中,而造父变星通常位于高密度的星系盘上.

此外,同样作为晚期局域测量手段的强引力透镜时间延迟,它所测量的哈勃常数却偏向早期宇宙观测结果,这是因为在选择透镜星系样本的时候就特意挑选了那些远离星系团的透镜星系,因而这些用来测量哈勃常数的强引力透镜样本天然地就处于低物质密度环境中.

基于这些观测事实及其所呈现的规律,我们有理由认为很有可能存在哈勃膨胀率与局域密度之间的正向关联.

4.2.1 变色龙暗能量模型

一种自然产生这种哈勃膨胀率与局域密度之间正向关联的理论模型是所谓变色龙暗能量[88],它起源于变色龙机制.最初提出变色龙机制的动机是出于在小尺度上高密度环境中屏蔽修改引力效应的目的.该机制假设一个标量场与局域物质密度以特定方式耦合,使得高密度环境下该标量场有效质量更大,即所传导的第五力力程更短,从而达到屏蔽第五种力的效果.但是变色龙机制还有一个伴生效应,即高密度环境下该标量场所处真空期望值的势能也更高,换而言之,其有效宇宙学常数也更大,从而局域哈勃膨胀率也更大(见图9).因此在这个模型中有效宇宙学常数随不同尺度的物质密度涨落改变而改变,但在某个固定尺度上它等效于宇宙学标准模型.

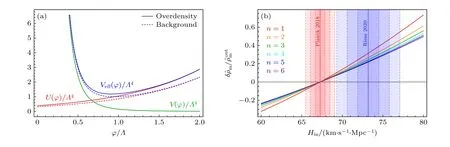
图9 变色龙暗能量机制示意图(a)变色龙暗能量有效势 Veff(φ)=V (φ)+U(φ),其中变色龙场势函数取 Peebles-Ratra 势函数 V (φ)=αΛ4(Λ/φ)n,变色龙耦合项取伸缩子耦合 U(φ)=exp(φ/Λ) .易见当实线对应的物质密度 大于虚线对应的物质密度时,相应地实线在有效势的真空期望值处对应的势函数值(真空能)也大于虚线的情况.(b)选取 Planck 2018 测量结果(红色)为背景宇宙学,那么局域物质密度超出(纵轴)对应的局域哈勃常数(横轴)可以拟合 SH0ES 测量结果(蓝色).图片来自文献[88]Fig.9.The illustrative demonstration of the chameleon dark energy model.(a)The effective potential of chameleon dark energy is Veff(φ)=V (φ)+U(φ),where the chameleon potential is of Peebles-Ratra form V (φ)=αΛ4(Λ/φ)n,and the chameleon coupling is of dilaton form U(φ)=exp(φ/Λ) .It is easy to see that when the solid curve corresponds to higher matter density than the dashed curve with lower one,then the potential energy (vacuum energy)at the vacuum expectation value of the effective potential is also higher than the dashed case.(b)Choosing the Planck 2018 result (red)as the background cosmology,then the corresponding local Hubble constant (horizontal axis)from given local matter density contrast (vertical axis)could fit the SH0ES result(blue).The figure comes from Ref.[88].

这样,利用处于高密度环境下的距离指示器样本测量本地的哈勃常数时会包括3 部分贡献: 一部分来自于我们自身所处的物质密度环境(在小尺度上这部分贡献偏向正);另一部分来自于我们和距离指示器样本之间的物质密度涨落之和(如果距离指示器样本足够远,这部分物质密度涨落贡献求和后应接近为零);最后一部分来自于距离指示器样本所处的物质密度环境(这部分贡献一般为正),因此最后测量得到的哈勃常数相对真正背景膨胀部分的贡献总是会更大.在这个物理图像中,早期测量哈勃常数更小是因为早期物质密度涨落也更小,它反映了真正背景膨胀的部分.

此外,S8问题在这个模型中也可以得到解释,即物质扰动增长越大,其局域的哈勃膨胀率也更快,从而反过来稀释了原来的物质扰动增长,最后达到平衡状态的S8自然比宇宙学标准模型所期望的更小.另外,正因为越高的局域物质密度涨落在晚期会被更大的局域宇宙学常数所稀释,因此它相对于全空间固定的宇宙学常数(即宇宙学标准模型)而言可以在高红移允许更大的物质密度涨落,从而自然解释了最近 JWST (James Webb space telescope)在高红移观测到的超出预期的大质量星系数密度.未来我们将在扰动水平上更细致地研究该模型(作为相互作用暗能量模型的一个特例).

4.2.2 尺度依赖暗能量

最后,回到宇宙学中可能被称为终极问题之一的宇宙学常数问题上来(另一个终极问题是宇宙的起源).一方面,宇宙在小尺度上由局域量子场论描述,其真空能量密度由有效宇宙学常数给出.具体来说,如果引力依然由经典引力的场方程描述,Gab+λbaregab=8πG〈Tab〉,其中由洛伦兹协变性,真空能对应的能量动量张量形式应为〈Tab〉=-〈ρ〉gab,其守恒方程∇aTab=0 意味着真空能量密度〈ρ〉是一个常数,该常数在有效场论中应由其紫外截断能标给出,比如.最后的场方程Gab+λeffgab=0 用一个包含裸宇宙学常数的有效宇宙学常数λeff=λbare+8πG〈ρ〉来描述真空能,比如λeff∼λbare+.

另一方面,宇宙在大尺度上满足宇宙学原理,因此可以用FLRW 度规ds2=-dt2+a(t)2δijdxidxj描述.对于当前暗能量占主导的宇宙,其尺度因子演化a(t)=a(0)eHt近似是指数膨胀,其中哈勃膨胀率定义了某个常数Λ,它受到了当前宇宙加速膨胀的观测限制.值得注意的是,只有将起源于极小尺度的有效宇宙学常数λeff等同为来源于极大尺度观测的Λ,即λeff=Λ,才会遇到所谓宇宙学常数的微调问题.但是没有理由认为在极小尺度上时空还是均匀且各向同性的(事实上时空在极小尺度上更可能是剧烈变化的),所以也就没有理由可以认同λeff=Λ,因而也从一开始就避免了宇宙学常数的微调问题.

因此,宇宙学常数问题的定义本身或许也为我们指明了它的出路,即有效宇宙学常数可能是一个尺度依赖的物理量,在极小尺度上,由于时空剧烈变化,它可以非常大;但在极大尺度上,由于时空趋于均匀且各向同性,也由于某种机制(如文献[99]),它平均到一个非常小的数值上.我们的变色龙暗能量模型也在某种程度上提供了一个类似的图景,即变色龙场与不同尺度下不同平均物质密度的耦合给出了大小不同的有效宇宙学常数,而哈勃常数问题正是这种物理图像在两个尺度(即CMB尺度和局部哈勃流尺度)上的反映.

5 结论

现代宇宙学经历了热大爆炸宇宙学、暴胀宇宙学以及精确宇宙学等历史阶段,终于形成了以暴胀、暗物质和暗能量为要素的宇宙学标准模型,即六参数 ΛCDM 模型.该模型能够大致拟合迄今为止从星系尺度到宇宙学尺度的长达百亿年宇宙学历史的几乎全部观测事实.但是作为一个唯象模型,其各要素的理论起源尚未可知,并且近年来愈发严重的哈勃常数危机和S8冲突对其提出了严峻挑战.然而危机也同时孕育着机遇,或许哈勃常数危机正是这样一种帮助我们一窥宇宙学标准模型底层(新)物理的历史机遇.

本文简要综述了哈勃常数问题的观测证据和模型构造,以及从观测和理论两方面给予我们的启示.我们的主要结论偏向于哈勃常数问题并非源自观测上的系统误差,而是某种未被理论模型化的新物理.然而对早期宇宙和晚期宇宙的大多数模型构造都受到了来自各种观测的强烈限制,目前来看,似乎仅有相互作用暗能量模型有希望成为同时解决H0冲突和S8冲突的候选者.本文最后介绍了一种特殊的相互作用暗能量模型,并从观测数据中发现它的初步证据.未来,大尺度巡天项目、下一代 CMB卫星以及我国的空间站望远镜计划终将为我们揭示哈勃常数危机的物理本质提供机会.