含主动约束阻尼悬臂梁两种减振机理的模拟∗
黎 明, 孙 伟, 刘 钺
(1.东北大学机械工程与自动化学院 沈阳,110819)
(2.东北大学航空动力装备振动及控制教育部重点实验室 沈阳,110819)
引 言
主动约束层阻尼减振是相对于被动约束阻尼减振的一种新的结构形式,其将普通的金属约束层替换为智能材料(常用的为压电材料),利用智能材料的作动力来增强夹在约束层和基体之间的黏弹性阻尼层的剪切变形,从而提高了减振能力[1-2]。主动约束层减振由于适用的频率范围宽、减振能力强,已在航空航天领域得到了广泛应用[3]。理解并能模拟主动约束阻尼减振的动力学机理是进行该项减振技术设计与实施的关键。
当前,已有学者[4-5]明确解释了主动约束阻尼层的减振机理,即主动约束阻尼同时包含了两种减振机理:①黏弹性阻尼层产生的剪切变形进而耗能;②压电约束层产生的反相位作动力阻滞了结构的振动。但是,对上述两种减振机理的有效模拟还未建立起来。
为了有效模拟主动约束阻尼减振的机理,必须创建合适的动力学分析模型,目前关于主动约束阻尼层结构的动力学建模已有大量研究。王攀等[6]利用有限元方法将对边约束主动约束层阻尼板划分为若干4 节点28 自由度板单元,并结合能量原理建立动力学模型。胡梦佳等[7]利用7 自由度平面矩形ACLD 单元建立了ACLD 板力学模型。Sarangi等[8]针对含主动约束层阻尼复合材料层合壳推导了机电耦合非线性有限元模型,并对其振动特性进行了分析。Xie 等[9]采用单层有限元模型来模拟ALCD 的3 层结构,且3 层均考虑剪切和轴向应变,应用能量法和拉格朗日公式求得ACLD 板模型的整体动力学方程。Sahoo 等[10]基于Galerkin 法和逐层理论创建了含椭圆主动约束阻尼层复合材料结构动力学有限元模型,并求解了复合结构动态特性。Li 等[11]将主动约束阻尼片的边缘用附加点质量的等效弹簧来模拟,用假定模态方法和拉格朗日方程推导了含主动约束阻尼片旋转梁的动力学模型。上述关于含主动约束阻尼层复合结构建模与分析的研究均是将ACLD 的作用转化为一种阻尼的影响来引入动力学模型中,与所描述的两种阻尼减振机理并不对应,但可作为本研究的参考。
笔者以部分贴敷主动约束阻尼层悬臂梁为对象,通过对主动约束层阻尼两种减振机理的模拟,建立了ACLD 悬臂梁的动力学模型,并组建了主动约束阻尼减振实验系统,用实验结果校验了ACLD 悬臂梁动力学模型的合理性。同时,对比分析了仅包含黏弹性约束阻尼或压电阻滞单一减振机制以及同时包含两种减振机制时复合梁的动力学响应特性。
1 主动约束层减振机理分析
以局部贴敷主动约束层阻尼悬臂梁为例,进一步解释该项减振技术的两种减振机理。悬臂梁主动约束阻尼减振原理如图1 所示,其工作过程描述如下:当梁受到激励产生振动时,压电传感层会因振动而产生电压,电压经电压采集装置传输给控制器;由控制器对数据进行处理后输出,将指定的控制信号输送给压电驱动装置;压电驱动装置按照接收到的信号对压电作动层施加电压,促使主动约束层阻尼对梁结构的振动进行抑制。整个减振效果可由附加的振动测试传感器来评价。
主动约束阻尼的两种减振机制,即中间黏弹性层剪切耗能和压电层对振动的反相阻滞作用,可通过分析ACLD 结构的受力及变形过程来描述。主动约束阻尼层的两种减振原理如图2 所示。当梁产生振动时,由于压电作动层与基体梁层的形变不同步,使得中间黏弹性阻尼层受到剪切,进而产生阻尼耗能。加载到压电作动层上的电压会让压电作动层因逆压电效应而产生拉伸或收缩变形,给予梁层一个反相阻滞力抑制梁的运动。在含主动约束阻尼层结构建模中,必须有效模拟上述两种减振机制才能再现该阻尼器的减振现象。

图2 主动约束阻尼层的两种减振原理Fig.2 Schematic diagram of two kinds of vibration reduction mechanisms in active constrained layer damping
2 局部贴敷ACLD 悬臂梁动力学建模与求解
图3 为部分主动约束层阻尼处理悬臂梁的示意图,以梁体下表面与截面中线交点为坐标原点建立坐标轴。其中:L为悬臂梁悬臂长度;b为梁宽;主动约束层阻尼贴敷在距离夹持端Lz处,长度为Lm;F为施加的外部扰动力。从有效模拟主动约束阻尼两种阻尼减振机理出发,采用有限元法,创建局部贴敷ACLD 悬臂梁结构动力学模型并进行求解。
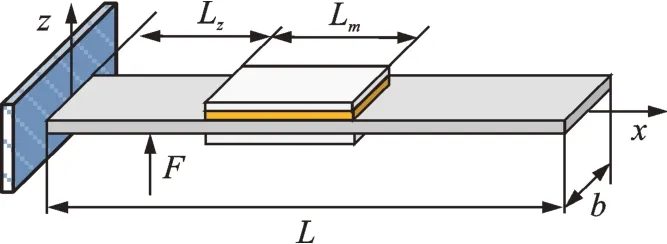
图3 部分主动约束层阻尼处理悬臂梁示意图Fig.3 Schematic diagram of partial active constrained layer damping treatment of cantilever beam
2.1 黏弹性层剪切耗能的模拟
这里用2 节点8 自由度单元模拟贴敷ACLD 部分的力学行为,ACLD 单元如图4 所示,其节点位移向量可表示为

图4 ACLD 单元Fig.4 ACLD element
其中:i,j为单元节点编号;w为挠度;θ为单元转角;u为轴向位移;角标c 和b 分别代表压电约束层和基体梁层;Le为单元长度。
单元内任一点位移同节点位移的关系可表示为
其中:Nw,Nb和Nc为各部分的形函数。
其中:ζ=x/Le为单元的局部坐标。
当梁体发生振动时,ACLD 单元会发生转动,此时会出现基体梁层和压电作动层的形变不一致,这使得中间的黏弹性阻尼层发生剪切,层间形变关系如图5 所示。其中:γ为黏弹性阻尼剪切应变;t为厚度;角标v 代表黏弹性阻尼层。
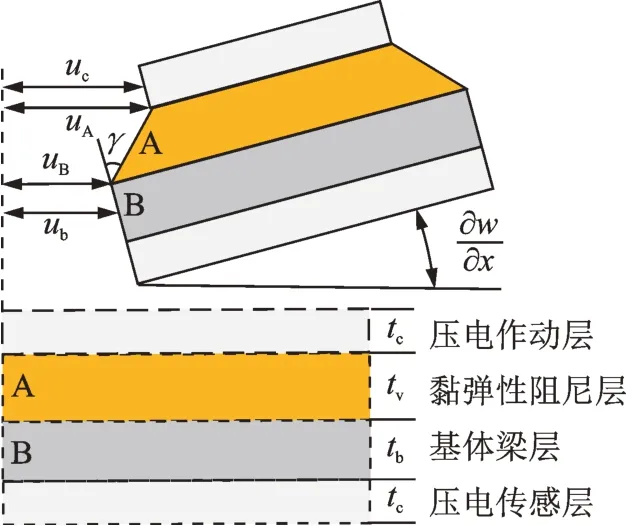
图5 层间形变关系Fig.5 Deformation relationship between layers
由几何关系可得
可以得到
黏弹性层任一点剪应变γ和轴向位移uv同样可以表示成形函数与节点位移向量的乘积形式,即
其中
从以上分析可知,式(6)描述了夹在基体及约束层之间的黏弹性层的剪切变形,可作为描述黏弹性剪切耗能的基础公式。得到各层形函数后,结合能量法,可得到各层的单元刚度与质量矩阵表达式为
其 中:的 下 标wmasub 可 替 换 为wb 和wc,代表梁层和约束层挠度部分产生的单元刚度矩阵;的下标umasub 可替换为ub 和uc,代表梁层和约束层轴向位移部分产生的单元刚度矩阵;Kve为黏弹性层的单元刚度矩阵;Mmeasub的 下 标masub 可 以 替换为wb,wc,wv,ub,uc 和uv,代表各层挠度和轴向位移部分对应的单元质量矩阵;Esub,Isub,ρsub和Asub的下标sub 可替换为c,v 和b,代表各层材料的弹性模量、截面惯性矩、材料密度和截面积;Gv为黏弹性阻 尼 剪 切 模 量;Νsfsub,Ns′fsub和Ns″fsub下 标sfsub 可 替 换为w,c,b,γ和v,代表形函数对x的1 阶导数和形函数对x的2 阶导数。
需要说明的是,这里压电传感层单元分析方法与压电作动层一致。最终,ACLD 单元的质量矩阵Me和刚度矩阵Ke可以表示为
其中:Mewb,Meub分别为基体梁挠度和轴向位移对应的单元质量矩阵;Mewv,Meuv分别为黏弹性层挠度和轴向位移对应的单元质量矩阵;Mewc,Meuc分别为压电层挠度和轴向位移对应的单元质量矩阵;Kewb,Keub分别为基体梁层挠度和轴向位移对应的单元刚度矩阵;Kev为黏弹性阻尼层剪切形变产生的单元刚度矩阵;Kewc,Keuc分别为压电层挠度和轴向位移对应的单元刚度矩阵。
黏弹性层的材料参数用复模量模型来模拟,即
其中:E*为复模量;ER为复模量实部;EI为复模量虚部;η为材料的损耗因子;i=。
这样,由式(10)求解出的单元刚度矩阵就会存在虚部,成为复刚度矩阵,表示为
其中:Ke*为复刚度矩阵;KeR为复刚度矩阵实部;KeI为复刚度矩阵虚部。
式(12)中的iηKeR代表ACLD 单元的阻尼,为了便于时域求解,可将其转化为等效黏性阻尼矩阵Ce,表示为
其中:ωex为激励频率。
悬臂梁结构中还含有非ACLD 单元,例如基体梁单元,可通过将式(10)中对应的压电片和黏弹性阻尼部分去掉得到。同理,被动约束层阻尼单元以及主动控制单元也可通过对式(10)的调整得到。
2.2 压电阻滞减振的模拟
压电阻滞力的作用是在外扰力对结构进行激励时,提供一个与外扰力相斥的作用,从而降低外扰力对结构的影响。压电阻滞力是由于压电作动器受到电压后因逆压电效应发生形变而产生的。
压电材料受到电压影响后会产生形变,二者之间的关系可由压电第2 类方程[12]表示为
其中:σ为应力;D为电位移量;S为应变;为电场强度;cE为弹性刚度矩阵;e为压电应力系数矩阵;εS为介电常数矩阵。
假如因振动产生的形变可以忽略不计,则压电作动器受到电压后产生的应力为
若考虑压电作动器为厚度方向受到极化,关注其在1 维轴向的形变,则1 维数值表达式为
其中:e31为压电应力系数为厚度方向的电场强度,=Vc( )t/tc,Vc(t)为施加的电压值,可由实验测得。
压电作动器产生的力矩Mmo可表示为
综上,可得到单元的阻滞力向量为
式(18)即为能削弱外扰力对结构作用的压电阻滞力,由此描述出主动约束阻尼减振中压电层的阻滞减振机理。
2.3 整体运动方程的建立与求解
整体结构还受到激振源的激励,外力所做的虚功可以表示为
结合前述求解得到的单元质量、刚度、阻尼矩阵以及压电阻滞力,可将主动约束层阻尼单元动力学方程写为如下形式
组集后可得到整体的动力学平衡方程为
此整体动力学方程包含了所描述的两种减振机理,可以有效预测主动约束层阻尼结构的减振效果。另外,还可根据需求通过改变等式中的项来模拟被动约束层减振、纯主动减振以及不加减振措施等情况。
当式(21)右侧的两个力均为0 且不考虑阻尼时,可变为下列形式来求解系统固有频率
其中:ωi为各阶固有频率;ψi为对应阶次固有振型。
可以应用Newmark-β 法对整体动力学方程的时域进行求解
3 实 例
这里以部分主动约束层阻尼处理悬臂铝梁为例,创建本研究提出的包含模拟两种减振机理的动力学模型,并做相应的求解与分析。悬臂梁一端固定在专用夹具中(夹持区为50 mm),在距离夹持端125 mm 处进行主动约束层阻尼处理,所用的压电材料为PZT-5H,黏弹性材料为ZN-1,激振器激励点距夹持端52.5 mm,拾振点选取在距自由端25 mm处。试件几何参数及材料参数如表1 所示。

表1 试件几何参数及材料参数Tab.1 Geometric and material parameters of the test specimen
所搭建的主动约束阻尼减振实验系统如图6 所示,整体实验系统包含振动激励、数据采集和主动控制等部分。振动激励主要包括PCB 模态力锤和联能JZK-2柔性杆激振器,其中模态力锤用于锤击实验,柔性杆激振器用于提供稳态谐振激励。数据采集部分主要有B&K 4517加速度传感器,用于拾取振动信号,LMS 16通道便携式数据前端用于采集振动信号。主动控制部分主要由NI电压采集硬件、控制器以及压电驱动电源组成,其中NI硬件设备负责采集由压电传感器产生的电压以及将控制器处理后的控制信号进行输出,控制器用于对采集信号进行运算处理,压电驱动电源用于对信号进行放大后施加到压电作动层。控制器利用LabVIEW 软件进行编写,控制率为比例控制。该实验系统的主要仪器设备见表2。

图6 主动约束阻尼减振实验系统Fig.6 Active constrained layer damping vibration reduction experimental system
应用上述实验系统对部分主动约束层阻尼处理悬臂梁进行固有频率及定频时域响应测试,相关结果用于校验所创建的分析模型的合理性。
3.1 主动约束层阻尼悬臂梁固有频率求解
将ACLD 悬臂梁划分为70 个单元,共168 个自由度,按照式(9)和式(10)求解ACLD 单元及普通梁单元的刚度及质量矩阵,再基于式(22)求解悬臂梁系统的固有频率,整个程序利用Matlab 软件编制。考虑到主动约束层阻尼减振中压电阻滞对低阶频率的减振效果好,所以这里主要关注100 Hz 以内阶次的情况。计算与实测的ACLD 悬臂梁固有频率比对如表3 所示。
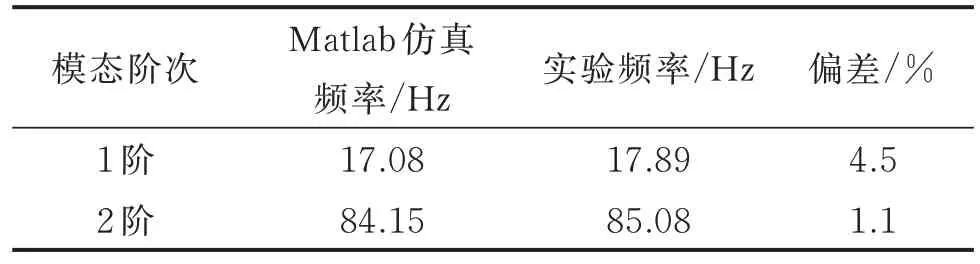
表3 计算与实测的ACLD 悬臂梁固有频率比对Tab.3 Comparison of calculated and measured natural frequencies of ACLD cantilever beam
从表3 可以看出,在固有频率方面,偏差均在5%以内,偏差较小,参照文献[13-14]可认为仿真结果与实验结果对比良好,从而证明了所建立ACLD单元的合理性。
3.2 主动约束层阻尼悬臂梁振动响应求解
这里将激振频率分别设定为1 阶共振频率及其附近的两个非共振频率点,进行时域响应求解,并将求解结果与实验进行对比。激振频率及压电作动层受到的电压峰值如表4 所示,其中17.0 Hz 为1 阶共振频率,各电压值是由压电传感器实测得到的。

表4 激振频率及压电作动层受到的电压峰值Tab.4 The excitation frequency and the peak voltage of the piezoelectric actuating layer
对比的时域响应包含两种工况,分别是加主动控制前及加主动控制后。其中:加主动控制前可视为被动约束阻尼减振系统,对其建模可仅考虑黏弹性层剪切耗能机理;加主动控制后对其建模分析则需同时考虑所描述的两种减振机理。不同频率下仿真计算与实验结果对比如图7~9 所示。

图7 16.7 Hz 仿真结果与实验结果对比Fig.7 Comparison of simulation and experimental results at 16.7 Hz

图8 1 阶共振频率下仿真结果与实验结果对比Fig.8 Comparison of simulation and experimental results at the first order resonance

图9 17.2 Hz 仿真结果与实验结果对比Fig.9 Comparison of simulation and experimental results at 17.2 Hz
施加控制前后各频率仿真与实验响应结果对比如表5,6 所示,其中17.0 Hz 为1 阶共振频率。各频率下未控制结构对比偏差最大为18.9%,施加控制后的结果对比偏差最大为18.6%。总体上看,仿真与实验对比偏差均在20%以内,参考文献[15-16]可认为此偏差可以接受。仿真模型再现了实验观测到的主动约束阻尼减振现象,对两种减振机制的模拟是合理的。在施加主动控制时,所需的压电参数直接引用了表1 中厂家提供的数据,可能与实际所需的参数有偏差,导致仿真结果与实验结果偏差较未控制时有所增大。
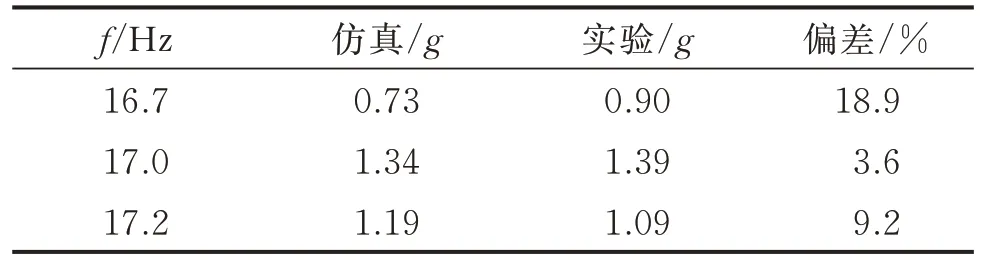
表5 未施加控制时各频率仿真与实验响应结果对比Tab.5 Comparison of simulation and experimental response results of each frequency without control
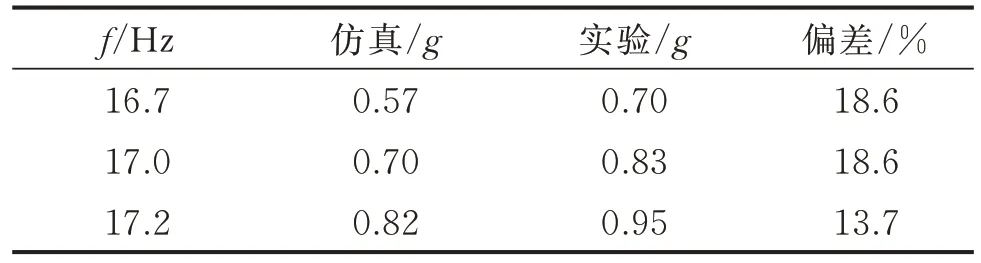
表6 施加控制时各频率仿真与实验响应结果对比Tab.6 Comparison of simulation and experimental response results of each frequency when the control is applied
3.3 各种减振处理的仿真对比
本研究所创建的包含两种减振机理的局部ACLD 处理悬臂梁动力学模型是一个通用模型,在对单元刚度及质量矩阵调整后,也可模拟无减振措施、被动约束层阻尼处理和主动控制减振的情况。针对处理层大小与位置相同、尺寸相同的试件,在1 阶共振的激励条件下,各种处理情况响应仿真结果和幅值分别如图10 和表7 所示。
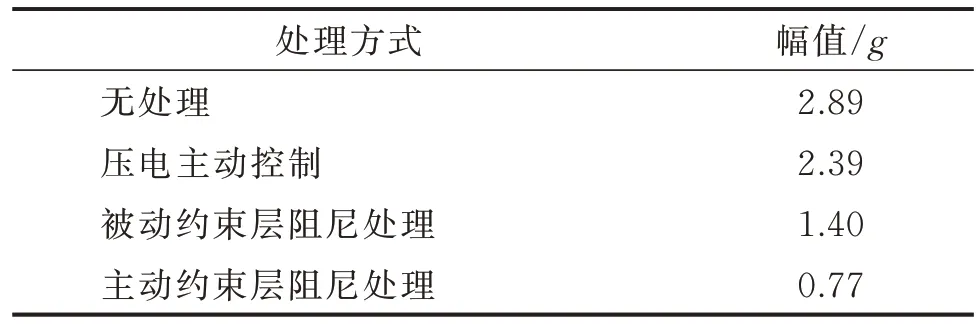
表7 各种处理情况下的幅值Tab.7 Amplitude values under various treatment conditions
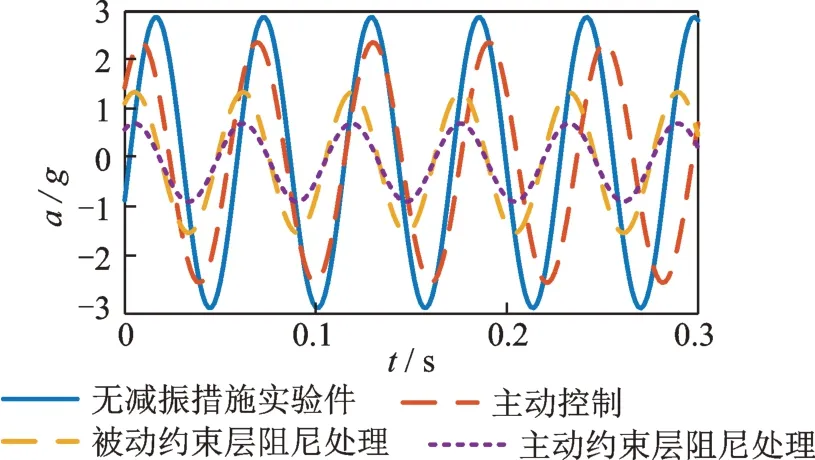
图10 各种处理情况响应仿真结果对比Fig.10 Comparison of simulation results under various processing conditions
从图10 可以看出,由于包含两种阻尼减振机制,主动约束层阻尼处理减振效果最好,其振动幅值最小,优于被动约束层阻尼处理以及单纯的压电主动控制情况。对于本实例,相比于无处理的实验件,压电主动控制的幅值减少了17.3%,被动约束层阻尼处理减小了51.6%,而主动约束层阻尼在被动约束层阻尼处理减振的基础上又将幅值减小了45%,与无处理情况相比减少了73.4%。
4 结 论
1) 提出了模拟主动约束阻尼振动控制方法中两种减振机理的分析模型:用形函数表达出黏弹性层的剪切变形,并采用复模量模型将等效阻尼矩阵分离出来以模拟黏弹性层剪切耗能;利用压电方程与力学公式推导出压电阻滞力以模拟压电反相阻滞减振。创建出包含两种阻尼减振机理的通用ACLD处理悬臂梁动力学分析模型。
2) 组建了ACLD 处理悬臂梁实验系统以校验所创建的动力学模型的合理性。结果表明,共振及非共振激励频率下,施加控制后的仿真结果与实验值对比最大偏差为18.6%,因而可认为仿真模型再现了实验观测到的主动约束阻尼减振现象,所描述的对两种减振机制的模拟是合理的。
3) 基于所创建的包含两种阻尼减振机理的通用动力学分析模型,通过调整单元矩阵,分别模拟并对比分析了无减振措施、被动约束层阻尼处理、主动控制和主动约束阻尼处理悬臂梁的时域振动响应。结果表明,主动约束阻尼由于同时包含两种减振机理,其减振效果要优于其他仅包含单一减振机理的振动控制方法,相比于无减振措施,振动幅值减少了73.4%。

