面向分布式组网无人机集群的感知数据融合方法

吕大鑫，杨超群

（1. 电磁空间安全全国重点实验室，嘉兴 314033；2. 中国电子科技集团公司第三十六研究所，嘉兴 314033；3. 东南大学自动化学院，南京 210096）

1 引 言

近年来，随着无人机自主飞行、人工智能、集群控制、先进通信等技术的广泛发展，无人机集群在战场中的作用潜力愈发凸显［1］，无人机集群作战已被认为是未来空战的重要作战方式之一［2］。无人机集群是指由一组具备自主或部分自主能力的无人机，借助人工智能、协同探测、数据融合、联合组网、分布控制、智能决策等技术，组成的具有一定的群体智能、可执行复杂任务的集群系统［3］。无人机集群具有成本低、自主程度高、生存能力强、灵活度高等优势［4-5］，已引起了国内外学术界、工业界及政府军方的广泛重视，并已在交通物流、娱乐表演、国土防御、军事作战等领域投入使用。典型的例子包括：2022 年北京冬奥会开幕式上，2022 架无人机组成的集群展示出漫天雪花、冬奥会徽的惊艳表演；2022 年俄乌冲突中，双方数十种型号的数百架侦察、打击无人机在战场中上演真实的高强度攻防对抗［6］。

无人机集群中无人机之间的通信组网方式可分为集中式和分布式两种。集中式组网表示多架无人机之间需要通过一个集中的网络设备或中心主机进行数据交换，在复杂的高空动态环境中，极易带来通信距离限制、数据传输的数据拥塞和可靠性差的问题［4］。分布式组网如Ad-Hoc网络等具备去中心、自组织、动态拓扑等特性，各无人机通信节点地位平等，系统内单个节点故障不会对整体造成影响，节点之间传输数据量小且生存能力强［4］。因此，分布式组网的通信方式越来越受到无人机集群研究人员的关注。

由于单个无人机的感知能力有限，为对监视区域获得更为准确全面的感知信息，无人机集群通常需要对单个无人机的感知信息进行数据融合。然而，不同于集中式组网无人机集群，分布式组网无人机集群由于中心主机的缺乏、全局知识的缺失、通信限制、各无人机感知信息的相关性未知，使得数据融合的难度大为增加［7］。此外，各无人机相对独立的分布式数据融合还将带来感知信息的重复融合问题。因此，近年来不少学者对面向分布式组网无人机集群的分布式数据融合展开了研究。针对分布式无人机系统中的感知信息不一致的问题，文献［8］提出了基于最大一致性协议的快速实现整体信息一致性的分布式数据融合方法，并证明了该方法的收敛性和实现最大一致性的条件；文献［9］提出了一种基于非线性分布式混合信息滤波框架的分布式无人机协同目标感知技术，实现了非线性场景中对目标的稳定跟踪，并给出了实现随机稳定性的条件；文献［10］提出了基于分布式仿生集群算法和协同搜寻优化策略的主动感知方法，该方法采用分布式目标搜寻算法降低环境和目标特性对无人机集群的探测性能的影响，同时引入自适应算子的差分进化算法提取环境信息，改善无人机集群的控制性能。然而，对于如何进行准确的、有效的、稳健的分布式数据融合，目前的研究仍尚不充分。

为解决分布式组网无人机集群中的分布式数据融合问题，本文提出了一种基于一致性理论、算术平均理论和标签随机有限集（Labeled Random Finite Set，LRFS）理论的分布式数据融合算法——一致性算术平均标签多伯努利融合算法。该算法首先采用LRFS概率密度函数描述各无人机的局部感知信息，其次采用算术平均理论作为计算全局融合感知信息的准则，最后提出采用分步骤的一致性方法在相邻无人机之间进行迭代融合，完成对全局感知信息的计算。

2 问题建模

2.1 系统模型

考虑如图1所示的分布式组网无人机集群，该集群由大量具有感知、通信和信息处理功能的无人机组成。

图1 分布式组网无人机集群示例Fig.1 The illustration of the distribution UAV swarm system

从数学的角度上看，图1所示的分布式组网无人机集群可看作一个图网络G=(N，A)，其中，N表示网络的节点即无人机的集合，A表示网络的边即无人机之间的通信链路的集合。集群中无人机的数目可用|N|表示，且可用(i，j)表示无人机i可接收无人机j的数据。对任意无人机i而言，用Ni表示其邻点的集合，即其可接收到数据的所有无人机的集合，特别地，N(j)i表示不包含其自身的邻点的集合。

2.2 求解目标

在当前时刻k，假定用随机有限集（Random Finite Set， RFS）Xk={x1···，xn}表示当前时刻监视区域内目标的集合，用RFS 概率密度函数πi(Xk)表示任意无人机i对监视区域内上述目标的感知结果，其中n表示当前目标数目，xj=(xj，lj)表示第j个目标在当前时刻的状态，包括动力学状态xj∈X和标签lj∈L，前者描述了该目标的位置、速度、加速度等信息，后者描述了用于唯一鉴别该目标的身份信息，X和L分别表示动力学状态空间和标签空间。

对于Xk，进一步定义标签映射函数L：X×L→L，即有L(Xk)={l1，···，ln}。特别地，若Xk满足标签互异的条件，即

式中，| · |表示求势操作，即求集合中元素的数目，则认为Xk是一个LRFS。在后文中，为表述方便，定义如下两个指示函数：

（1）标签互异指示函数［11-12］

式中，δ(·)表示狄拉克函数。标签互异是指在集合Xk={x1，···，xn}中，每个元素xj=(xj，lj)的标签lj均不相同，只有在这种情况下，Xk和L(Xk)的元素个数才会相等，从而式（2）成立。

（2）隶属指示函数［13-14］

在当前时刻k，任意无人机i将对监视区域内多个目标进行感知，获得量测Zik，并利用量测信息更新感知结果πi(Xk)，具体的更新可用如下贝叶斯公式实现［13-14］

式中，πi(Xk-1) 表示上一时刻的感知结果，f(Xk|Xk-1)和分别表示监视区域内多目标的马尔科夫转移密度函数和无人机i的多目标似然函数。

由于单个无人机的感知能力有限，为对监视区域获得更为准确全面的感知信息，图1 中的分布式组网无人机集群需要对单个无人机的感知结果进行数据融合，即需要融合πi(Xk)以获得全局的感知结果(Xk)。然而，在分布式组网无人机集群中，全局的感知结果通常难以求解，其原因如下：

（1）集群内不存在可获取所有无人机感知结果的中心主机，这意味着每个无人机都只能依靠其邻点的感知结果进行融合。为此，需保证集群内所有无人机的融合结果可达到集体认同。

（2）各个无人机的感知结果的相关性通常未知，而且难以计算。以集群中的无人机i的感知结果πi(Xk)和无人机j的感知结果πj(Xk)为例，二者通常不是相互独立的，而是具有一定的相关性［7，12］。为进行融合，需采用如下公式

该公式表明二者的公共信息需被移除，然而在上述分布式组网无人机集群中，该公共信息难以有效移除。

3 一致性算术平均标签多伯努利算法

为解决分布式组网无人机集群中的感知数据融合问题，本节展示本文提出的一种称之为一致性算术平均标签多伯努利（Consensus Arithmetic Average Labeled Multi-Bernoulli Filter） 的分布式数据融合算法，以融合单个无人机的感知结果πi(Xk)，并获得全局的感知结果-π(Xk)。

3.1 单无人机局部感知

作为预备知识，首先介绍伯努利（Bernoulli）RFS、多伯努利（Multi-Bernoulli，MB）RFS 和标签多伯努利（Labeled Multi-Bernoulli， LMB）RFS。一个伯努利RFSX是指一个RFS 具有概率1 -r为空集，具有概率r为仅包含一个元素且该元素服从概率分布p(x)的集合，因此，其概率密度函数可表述为［12］

一个MB RFSX是M个相互独立的伯努利RFS的并集，即。因此，一个MB RFS 可用参数集完全表征［15］。若对MB RFS中的每一个非空项赋予独特的标签l∈L，则可得到一个LMB RFSX，其概率密度函数可表述为［16］

式中，

式中，L表示标签空间。为方便表述，式（7）可简写为π(X) ={rl，pl}l∈L或记作π(X) =(r，p)。

在当前时刻k，任意无人机i将对监视区域内多个目标进行感知，获得量测Zik，并利用量测信息更新感知结果πi(Xk)，具体的更新可采用式（4）所示的贝叶斯公式实现。然而，该公式涉及到集合积分，通常难以求解，为此，文献［17］提出了标签多伯努利滤波器，作为式（4）所示的贝叶斯公式的近似解。该滤波器平衡了计算复杂度与计算精度的矛盾，并提供了多个目标的标签信息，因此，本文采用标签多伯努利滤波器作为单无人机获取局部感知结果的手段。标签多伯努利滤波器可分为预测与更新两个步骤，需要说明的是，由于下述步骤均是在当前时刻k运行，为描述方便，以下忽略下标k，并用下标+代替下标k|k- 1。

预测：假定上一时刻该无人机对监视区域内多个目标的感知结果πi(Xk)和该区域新生目标的概率密度πB(X)均可用一个LMB RFS 表示。特别地，前者定义在动力学状态空间X和标签空间L上，由{rl，pl}l∈L表征，如式（7）～（8） 所示。后者定义在动力学状态空间X和标签空间B上，由{rl，B，pl，B}l∈B表征，如下所示：

则预测的感知结果是一个定义在状态空间X和标签空间L+=B∪L的LMB RFS，且具有参数集为

式中，

式中，符号＜·，·＞表示内积运算，pS(·，l) 和f(x| · ，l)分别表示标签为l的目标的存活概率和马尔科夫转移密度函数。

更新：首先式（10）可重新整理为

其次，在该无人机获得量测Zjk后，更新后的感知结果可用定义在空间X×L+的且具有如下参数集的LMB RFS近似，

式中，

式中，pD(x，l)表示具有标签l的目标检测概率，g(z|x，l)表示具有标签l的目标的似然函数，κ表示服从期望为λ的泊松分布的杂波的强度。进一步地，ΘI+表示从目标标签到观测的分配θ的集合，即I+→{0，1，…，|Z|}。特别地，分配θ具有性质为θ(i) =θ(i')⇒i=i'。

3.2 算术平均标签多伯努利RFS融合准则

对于RFS 概率密度而言，存在两种融合准则：几何平均（Geometric Average，GA）和算术平均（Arithmetic Average，AA）［18］。相较于传统的几何平均融合准则，近年来，李天成等提出的算术平均被证明是实现最小信息损失（Minimum Information Loss）融合的有效方法，在计算复杂度等方面存在优势［18-19］，且在数据融合领域展现出较强的应用潜力。因此，本文采用算术平均融合准则，该准则如下。

定理1. AA 融合准则：若多个传感器的局部RFS 概率密度为πi(X)，其中i∈N，N表示所有传感器集合，则AA 融合得到的全局RFS 概率密度为

证.参见文献［19］。

基于定理1，文献［20］进一步推导出如下LMB RFS的概率密度AA融合准则。

定理2.LMB RFS的概率密度AA融合准则：若多个传感器的局部LMB RFS 概率密度为πi=，其中i∈N，N表示所有传感器集合，且所有的局部LMB RFS 概率密度均定义在相同的标签空间L上，则AA融合得到的全局LMB RFS概率密度为，其中

证.参见文献［20］。

定理2为解决无人机集群中的感知数据融合问题提供了方向，然而，该定理无法直接用于分布式组网无人机集群的感知数据融合，其原因在于分布式组网无人机集群缺乏中心，各无人机只能获取其邻域无人机的感知结果，无法获取所有集群中无人机的感知结果，故无法达到定理2所示的全局感知结果。尽管一致性可用于实现在上述分布式组网集群中迭代计算全局感知结果，但并不能直接用于求解定理2 中的结果，原因如下：

上述原因使得一致性难以应用。

3.3 一致性算术平均标签多伯努利数据融合算法

为求解以LMB RFS 的概率密度表示的单个无人机感知数据分布式融合问题，本小节详细阐述本文所提的一致性算术平均标签多伯努利数据融合算法。首先由定理2 可推导出如下均匀权重的LMB RFS的概率密度AA融合准则。

定理3. 均匀权重的LMB RFS 的概率密度AA融合准则：若多个传感器的局部LMB RFS 概率密度为，其中i∈N，N表示所有传感器集合，且所有的局部LMB RFS 概率密度均定义在相同的标签空间L上，则AA融合得到的均匀权重的全局LMB RFS 概率密度为，其中

证.令ωi= 1/|N|，代入式（16）即可得

证明完毕。

式中，N(x；a，b)表示x服从均值为a、方差为b的高斯分布，αij表示权重，Jil表示高斯项的数目。则对于具有高斯混合近似的概率密度，定理3 中均匀权重的全局LMB RFS 概率密度为-π=，其中的可推导为

一方面，对于形如式（15）～（20）的求和问题，在分布式系统中可采用一致性算法求解。一致性算法的思想是通过每一个节点迭代更新并传输其本地信息给其邻域的节点，从而在整个分布网络中达成集体认同。另一方面，采用均匀权重，对全局融合结果参数与进行了部分解耦，使得可以对其分开进行一致性计算。因此，基于定理3 和一致性原理，在每个无人机都计算出LMB RFS 的局部感知的基础上，本文提出了如下分步骤的一致性算术平均标签多伯努利数据融合算法。

步骤1：局部感知：分布式组网无人机集群中的任意无人机i分别采用式（8）～（13）计算LMB RFS 形式的局部感知结果，计算并保存πi=(ri，pi)；

（a）信息交换。集群中任意无人机i均将其上一次迭代后的ril，c-1发送给其邻域无人机，其中；

（b）一致性迭代。计算

式中，ωij表示一致性权重，满足

记Ω为一致性矩阵，其第i行j列元素为ωij，则若为素阵和双随机矩阵［7］，一致性算法将趋于整体均值，即有

（a）信息交换。集群中任意无人机i均将其上一次迭代后的发送给邻域无人机，其中；

（b）一致性迭代。计算

式中，ωij同样表示一致性权重，且满足式（23），则一致性算法将趋于整体均值，即有

步骤4：全局感知融合输出：由定理3 和一致性原理可知，在分布式组网无人机集群中，所有无人机的全局感知融合将达成集体认同。经步骤1～3的计算，其全局感知融合结果仍可用LMB RFS概率密度表示为

4 仿真结果及分析

仿真条件如下。考虑由3架无人机构成的分布式组网无人机集群，对［-500，500］m×［-500，500］m二维区域内的目标进行跟踪，如图2 所示。区域内目标数目为1，且具有马尔科夫转移密度f(xk|xk-1)=N(xk；Fxk-1，Q)， 其中，xk=[x，ẋ，y，ẏ]T，(x，y)和(ẋ，ẏ)分别表示包括目标二维平面的距离和速度，F为状态转移矩阵，N(x；a，b)表示x服从均值为a、方差为b的高斯分布，Q=I4。目标的初始状态为x0=[0，0，0，5]T，即目标在y轴方向具有5 m/s 的速度。

图2 仿真场景Fig.2 Simulation case

如图2所示，该无人机集群为分布式组网，无融合中心或主机，各无人机之间通过网络进行信息传递。每架无人机携带传感器对该目标进行测量，测量的似然函数为g(zk|xk)=N(Hxk，R)，其中，H为观测矩阵。对于3架无人机，其检测概率均设为0.98，观测噪声方差分别设为：R1 =0.01I2，R2 = 0.04I2和R3 = 0.09I2。

每架无人机在接收到量测zk之后，运行一致性算术平均标签多伯努利数据融合算法，即先对目标进行局部感知，再进行融合，最后得到对目标信息的全局感知结果，其中每架无人机的一致性迭代次数设置为C= 40。

仿真结果如图3～5所示。其中，图3～4分别表示各无人机在进行一致性算术平均标签多伯努利算法后每个时刻对目标的x轴和y轴位置的感知结果。从图中可以看出，各无人机的感知结果均已达到一致性，即各无人机的全局感知结果均相同，说明了所提算法的有效性。

图3 各无人机各时刻x轴全局感知结果Fig.3 The x axis global sensing results of each UAV

图4 各无人机各时刻y轴全局感知结果Fig.4 The y axis global sensing results of each UAV

作为对比，图5～6 展示了各无人机未进行一致性算术平均标签多伯努利算法的局部感知结果与进行一致性算术平均标签多伯努利算法的全局感知结果，从图中可看出，全局感知结果对各无人机的局部感知结果进行了融合。

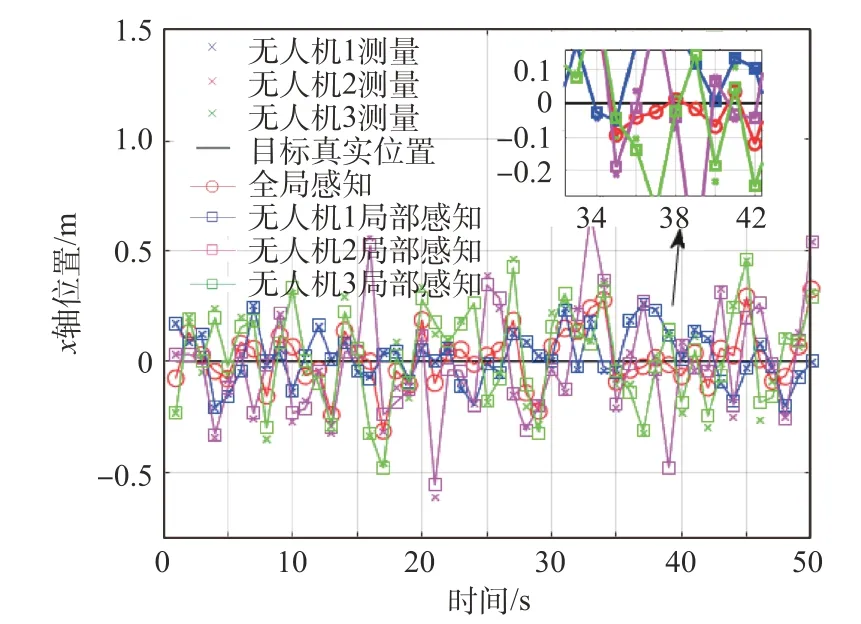
图5 各无人机各时刻x轴局部感知结果Fig.5 The x axis local sensing results of each UAV

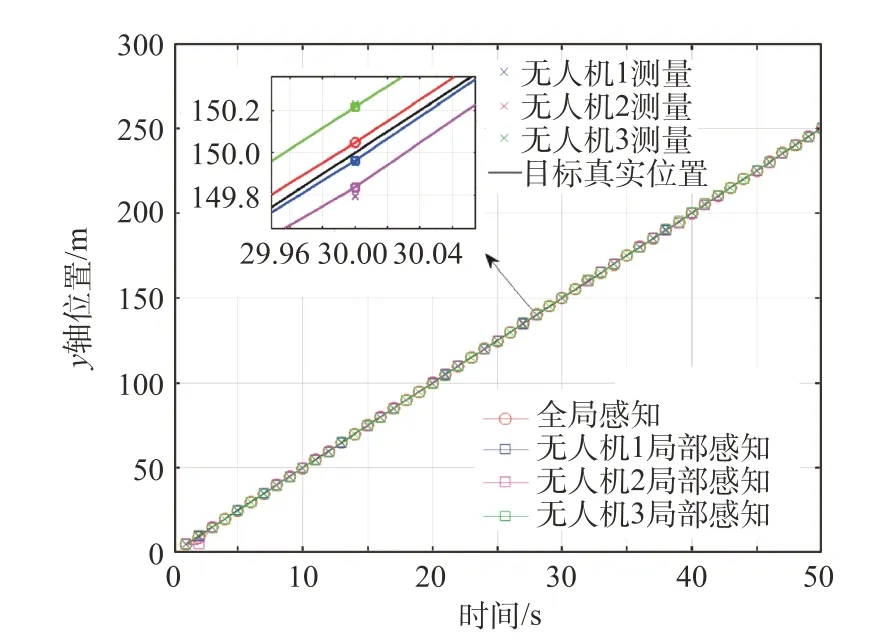
图6 各无人机各时刻y轴局部感知结果Fig.6 The y axis local sensing results of each UAV

为进一步定量验证所提算法的有效性，采用50 次蒙特卡洛实验，并统计其均方误差，所得结果如图7所示。由于3架无人机的观测噪声方差具有R1 ≺R2 ≺R3 的关系，因此3 架无人机的局部感知误差满足无人机1 的误差小于无人机2 的误差，且无人机2 的误差小于无人机3 的误差的关系。当采用所提算法进行融合时，在各无人机的观测噪声方差及其关系均不可知的情况下，所提算法实现了对局部感知结果的融合，并使得所有无人机的感知误差介于无人机1和无人机2的感知误差之间，起到了融合的效果。值得注意的是，由于各无人机的观测噪声方差及其关系均不可知，最优融合是不可达的，因此这种融合是保守的，但又是有意义的。它保证了各无人机达到了一个一致的、保守的、介于最优与最坏之间的全局感知结果。

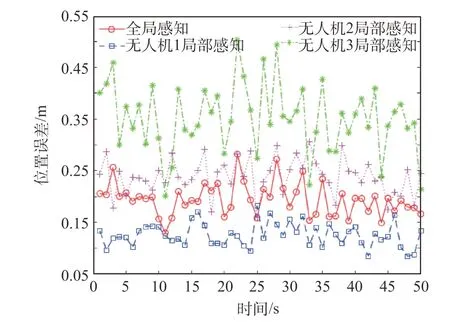
图7 各无人机各时刻位置均方误差Fig.7 Mean squared error of each UAV's position

5 结 论

本文针对分布式组网无人机集群中的数据融合问题，提出了一种基于一致性理论、算术平均理论和标签随机集理论的分布式数据融合方法——一致性算术平均标签多伯努利融合算法。该方法首先采用多目标概率密度函数描述各个无人机的感知信息，其次采用算术平均理论作为计算全局融合感知信息的准则，最后为实现在分布式组网无人机集群中计算全局融合感知信息，采用一致性的方法在相邻无人机之间进行迭代局部融合。仿真实验表明，该算法可实现分布式组网无人机集群中的数据融合。后续研究将考虑将该算法部署到实际无人机集群系统中，进行算法落地化应用。