基于连通性的三支密度峰值聚类算法

王江元,蔡明杰,2,祁明月

(1.湖南大学数学学院,湖南长沙 410082;2.湖南大学深圳研究院,广东深圳 518055;3.河北阅思信息科技有限公司,河北石家庄 050000)

聚类被视为最重要的无监督学习方法之一,用于在无标签数据中发现潜在结构。其最大优点是不需要先验信息就能够将对象集合分为彼此“相似”且与其他聚类中的对象“不相似”的群组[1],广泛用于图像分割[2]、文本挖掘[3]、生物信息学[4]、社区检测[5]等多个领域。

密度峰值聚类(DPC)[6]是一种经典的基于密度的聚类算法,基于2个假设实现聚类:一是密度峰值点的密度应当比其周围的点更高;二是密度峰值点与离其最近且比其密度高的点之间的距离应当比非峰值点与离其最近且比其密度高的点之间的距离更远。DPC的大致流程如下,先计算每个样本点的密度和到其他点的相对距离,再根据上述2个假设选择密度峰值点作为聚类中心点,最后将非中心点分配到离其最近且比其密度高的点所在的簇中。然而,DPC算法也存在着一定的局限性,例如,密度峰值点的选择问题和误分配问题。对于密度峰值点的选择问题,大多数改进算法通过改变密度以及距离的计算公式来解决[7-11]。对于误分配问题,一般通过改变分配策略对算法进行改进[12-14]。当处理流形结构的数据时,如果不使用路径距离,无论如何构造密度和距离的计算公式,总会出现同一类的样本被分配给不同簇的情况,因为仅根据邻域信息无法识别流形结构。若想利用路径距离,那么又会消耗大量的计算资源和时间,尤其是在处理大规模数据时。此外,计算路径距离前需要生成图结构,根据生成图的策略不同,或多或少还会损失原始数据的信息。

针对上述问题,本文提出了基于连通性的三支密度峰值聚类算法(CTW-DPC)。为了使DPC能够识别流形数据且不使用路径距离,引入连通性,通过三支聚类边界的连通性判断簇的连通性,合并被经典算法误分成多个簇的流形结构。对于经典算法无法发现的簇,提出在迭代过程中逐步发现低密度簇的方法,解决簇之间密度差异带来的问题。

1 相关工作

1.1 密度峰值聚类(DPC)

DPC算法作为中心聚类与密度聚类的结合体,以密度峰值点作为聚类中心,并在分配过程中使用密度聚类的思想。密度峰值点由局部密度和相对距离确定。对于数据集X,样本点xi的局部密度ρi的定义如下:

(1)

或

(2)

式中:χ为示性函数,当x<0时,χ(x)=1,当x≥0时,χ(x)=0;d(xi,xj)为样本点xi和xj之间的距离。局部距离δi通过计算比样本点xi密度高且离其最近的点之间的距离得到,定义为

(3)

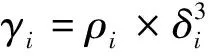
1.2 三支聚类

为了解决硬聚类的限制,即一个对象只属于一个簇,人们提出了许多软聚类方法。模糊均值聚类(FCM)[15-16]是最常用的软聚类方法,其假设簇由反映渐变边界的模糊集表示。另一个处理不确定性数据的有效工具是粗糙均值聚类算法(RKM)[17],它使用区间集表示具有模糊和不精确边界的簇,并假设一个对象必须属于1个下近似或者2个上近似的交集。尽管这个条件在粗糙集理论的背景下似乎是有效的,但对于一般的三支聚类来说,假设一个对象最多可以属于1个正域或者至少1个边界域似乎更为合理[18]。

基于三支决策[19],YU[20]提出了一种三支聚类模型,通过一对集合或3个集合来表示一个簇:考虑一对阈值(α,β)(α≥β)和一个评价函数φ(x),Ci是一个簇,U为一个论域,POS(Ci)={x∈U|φ(x)>α},BND(Ci)={x∈U|β≤φ(x)≤α},NEG(Ci)={x∈U|φ(x)<β}。由此定义的三支聚类对阈值的敏感性较大。WANG等[21]提出了三支聚类的理论框架,扩展了传统K-means算法和谱聚类算法,分别为CE3 K-means聚类和CE3谱聚类,这2种聚类都使用k近邻代替以阈值半径确定的邻域,来对正域和边界域进行判断。

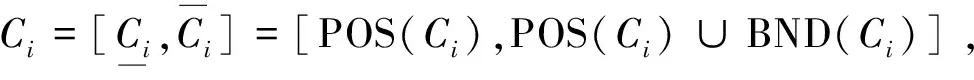
由于集合的正域需要利用某些关系对该集合进行粒化得到,因此需要由以下3个假设来确定簇的正域:

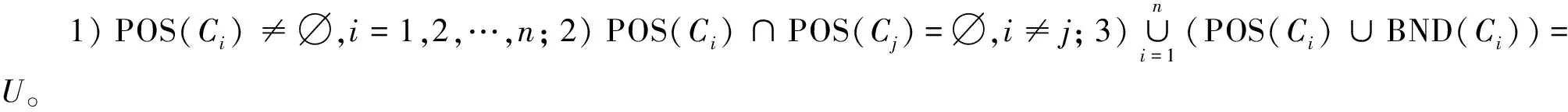
2 三支密度峰值聚类

通过改进DPC中的密度函数和分配策略,与三支聚类结合,提出一种改进的三支密度峰值聚类算法(TW-DPC)。对于TW-DPC生成的边界域,给出一种判断连通性的方式,使用连通分支概念对初始聚类结果进行合并。通过TW-DPC的反复迭代、连通性的判定与合并,发现TW-DPC无法探查到的低密度簇,实现CTW-DPC算法的高鲁棒性。

2.1 改进的三支密度峰值聚类

为了有效探查到不同密度的簇,减少迭代次数,提出一种新的密度函数。该度量利用反向k近邻(RKNN)定义。

定义1(反向k近邻) 样本点xi的反向k近邻定义为一类样本点x的集合,其k近邻中包含xi,即RKNN(xi)={x∈D|xi∈KNN(xi)}。

通过图1可以直观了解一个样本点的反向k近邻的构成。

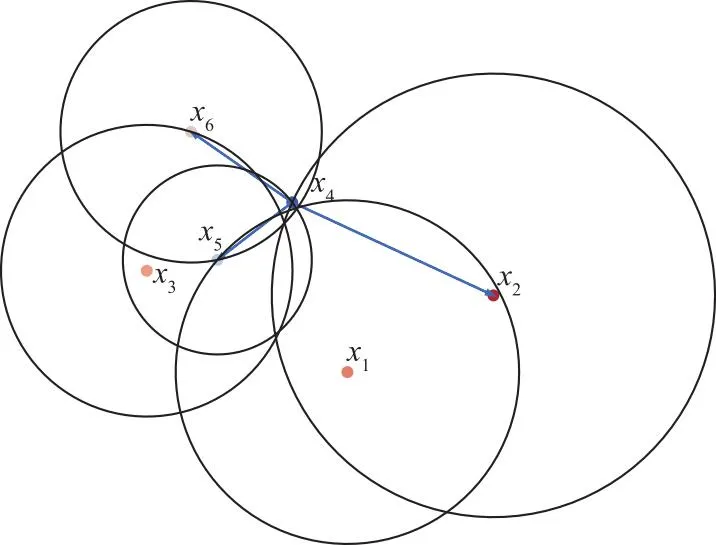
图1 反向k近邻示例,k=2

图1中样本由6个样本点组成,灰色的圆代表其圆心的2近邻。例如,x1的2近邻由x2和x5组成。蓝线代表的是x4的反向k近邻,即R2NN(x4)={x6,x5,x2}。从图1可以看出,反向k近邻的分布摆脱了距离限制,可以更好地反映邻域点到该点的连通性。一个样本点反向k近邻的基数越大,说明能够到达该点的点越多,并且同一个样本点的反向k近邻与k近邻的基数不必相同。

定义2对∀x∈X,令RKNN(x)和KNN(x)分别为x的反向k近邻与k近邻,则本文定义的密度为

(4)

上述定义将Sigmoid函数与KNN-DPC中的密度定义结合起来形成了新的密度定义。k近邻的基数越大时,密度也就越大。这种定义方式能够有效探查到低密度的簇。图2是在相同数据集下,TW-DPC与KNN-DPC不同定义下的密度分布图。可以看出,TW-DPC定义下的密度能够探查到圆环上的点作为密度峰值,而KNN-DPC中则无法识别圆环上的点。

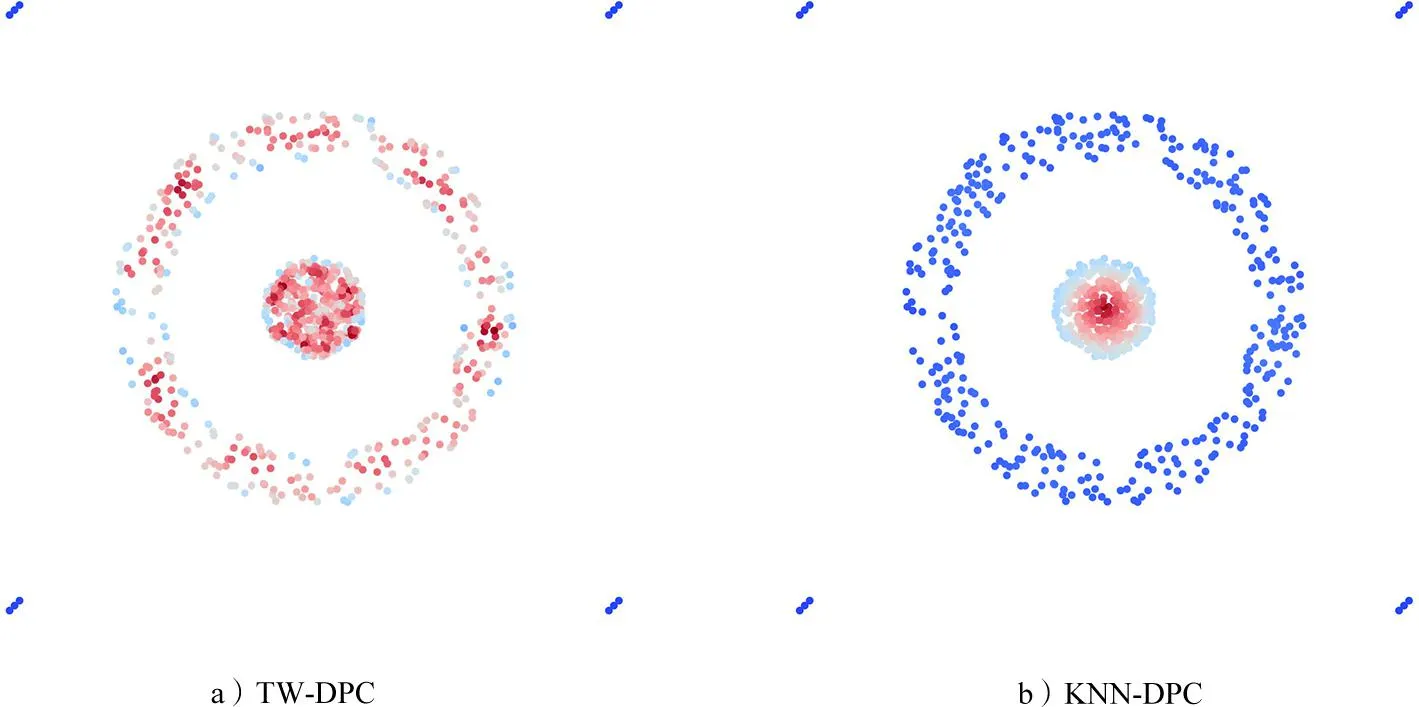
图2 2种密度函数比较图

对于相对距离函数δi,本文仍采取DPC算法中比样本点xi密度高且离其最近的点之间的距离作为相对距离函数。为了消除密度过传播带来的影响,本文采取RNN-DBSC[22]中的方式,即在分配过程中,计算将要扩展点的反向k近邻的基数,设置一个阈值α∈[0,+∞),对是否扩展进行判断。因为反向k近邻的基数在一定程度上反映了该点的连通性,因此通过控制阈值大小可以改变聚类结果的连通性。此外,本文引入互近邻定义,进一步增强连通性的判别方式。

定义3(互近邻) 对∀xi,xj∈X,称xj属于xi的互近邻,如果满足xj∈KNN(xi)且xj∈RKNN(xi)。

互近邻要求邻域内的点满足对称性,使得互近邻成为了一个等价关系。因此本文在分配过程中,使用互近邻对将要添加到搜索队列并被传递标签的点作出限制,使得被算法分到同一个簇的点在邻域关系层面上是等价的。这也与三支决策中正域的定义相吻合,即POS(X)={x∈X|[x]R⊆X},其中[x]R为等价关系R下x的等价类。

DPC因无法识别流形数据,导致一个连通流形上出现多个密度峰值点,即簇中心,这也导致在分配过程中,原本属于同一等价类的样本,因为从属于不同的簇中心而被分配到不同的簇。因此,本文引入三支聚类的边界域,对边界域内的点进行讨论,最终得到区间集形式的初始聚类结果。算法的大致流程如表1所示。

表1 算法的大致流程

2.2 基于连通性的聚类合并策略

使用TW-DPC得到簇的边界后,从边界点中选取m=min{k2,∑i|BND(Ci)|}个指标函数γ最大的边界点,作为判断边界连通性的代表点。本文采用的连通性判断指标仍然是代表点的反向k近邻基数,若基数大于k,则与该代表点的k近邻相交的簇在该点处连通,说明初始算法得到的聚类结果有误,即在一个簇中找到了多个密度峰值点,使得簇的正域识别有误。

通过上述操作得到初始聚类结果的连通性后,便可以构造簇之间的邻接图,再寻找邻接图的连通分支,将得到的极大连通分支作为合并后的聚类结果,并将所合并簇的最大密度的密度峰值点作为合并后新簇的簇中心。通过图3可以直观展现此合并过程。

图3 合并策略效果图

图3中,TW-DPC将数据集分为9个簇,通过计算簇的边界连通性,得到如图3 c)的邻接图,其极大连通分支为{C1,C2,C4,C8},{C3,C9},{C5,C6,C7},通过合并每个极大连通分支中的簇,得到如图3 d)所示的新簇。合并算法的伪代码如表2所示。

表2 合并算法的伪代码

2.3 CTW-DPC算法

由图3 a)可以发现存在4个未被TW-DPC识别的簇。针对TW-DPC在密度差异大的数据集上表现不良的问题,使用迭代过程,将密度差异大的簇分开识别。通过将未分配的点作为下一次迭代的数据集,屏蔽高密度簇对未分配数据的影响,并再次使用TW-DPC,达到在低密度水平下的聚类识别,提高算法的鲁棒性。本文最终提出的算法流程见表3。

表3 最终提出的算法流程

2.4 算法复杂度分析

本文提出的算法在TW-DPC部分主要计算所有样本点的k近邻、密度函数ρi以及距离函数δi,若样本的个数为N,那么计算时间的复杂度分别为O(NlogN),O(kN)和O(N)。而在合并算法中,使用三支决策计算聚类边界的时间复杂度为O(kN),若数据集的类别数为n,则判断连通性的最大时间复杂度为O(n2k)。通常情况下,每次迭代后的样本个数相比上一次大大减少,且k和n远远小于N,因此若算法的迭代次数为m,则算法总体的最大时间复杂度为O(mNlogN)。

3 实验结果与分析

为了检验本文提出算法的准确性,在18个数据集上与经典的DPC算法和5个改进的DPC算法进行对比试验。这18个数据集包括二维的人工数据集和来源于UCI的真实世界数据集,具体信息详见表4。由于进行对比的7个算法求得最优解时的参数不尽相同,因此本文采取网格搜索方式对各个算法的最优参数进行搜索。对于浮点型参数dc与α,搜索网格为{0.01,0.02,…,1}∪{1.1,1.2,…,5};对于整数型参数k,搜索网格为{2,3,…,50}∪{50,55,…,200}。实验评价指标采用调整兰德系数(ARI)和归一化互信息(NMI)。

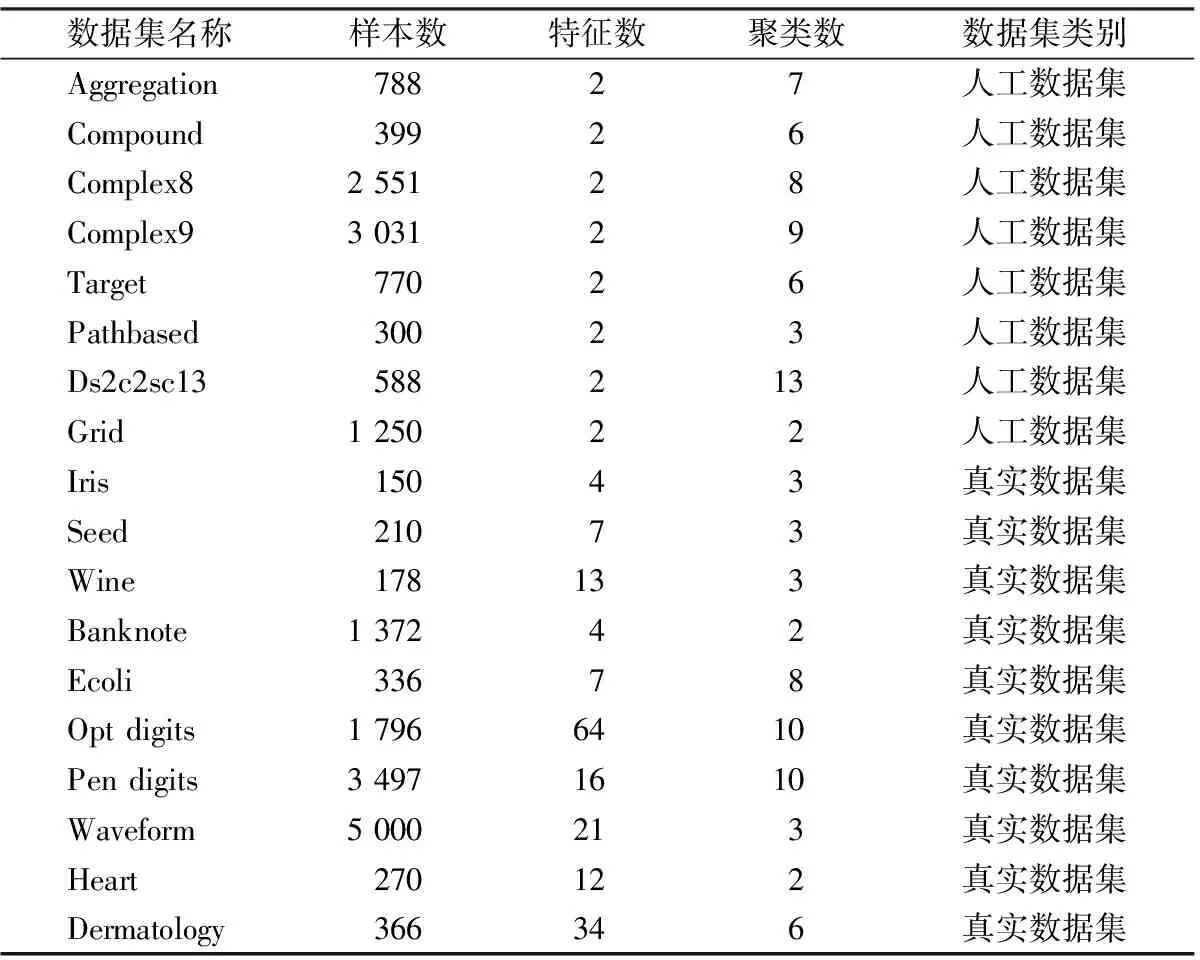
表4 实验数据集

3.1 人工数据集上的实验结果

CTW-DPC与其他6种算法在8种人工数据集上聚类结果的ARI和NMI如表5所示,其中加粗字体表示该结果为该数据集上最优算法下的评价指标,这2种指标越趋近于1,说明算法效果越好,当其等于1时,则说明算法的预测结果与数据集给出的标签完全一致。“—”表示该算法得不到有效的实验结果。由表5可以看出,本文提出的算法在这8个人工数据集上的表现都比较优秀,尤其是在流形数据集Compound,Complex8,Complex9上,比之前提出的算法都有明显提升。为了进一步展示实验效果,以数据集Compound为例,给出不同算法的实验对比图,如图4所示。

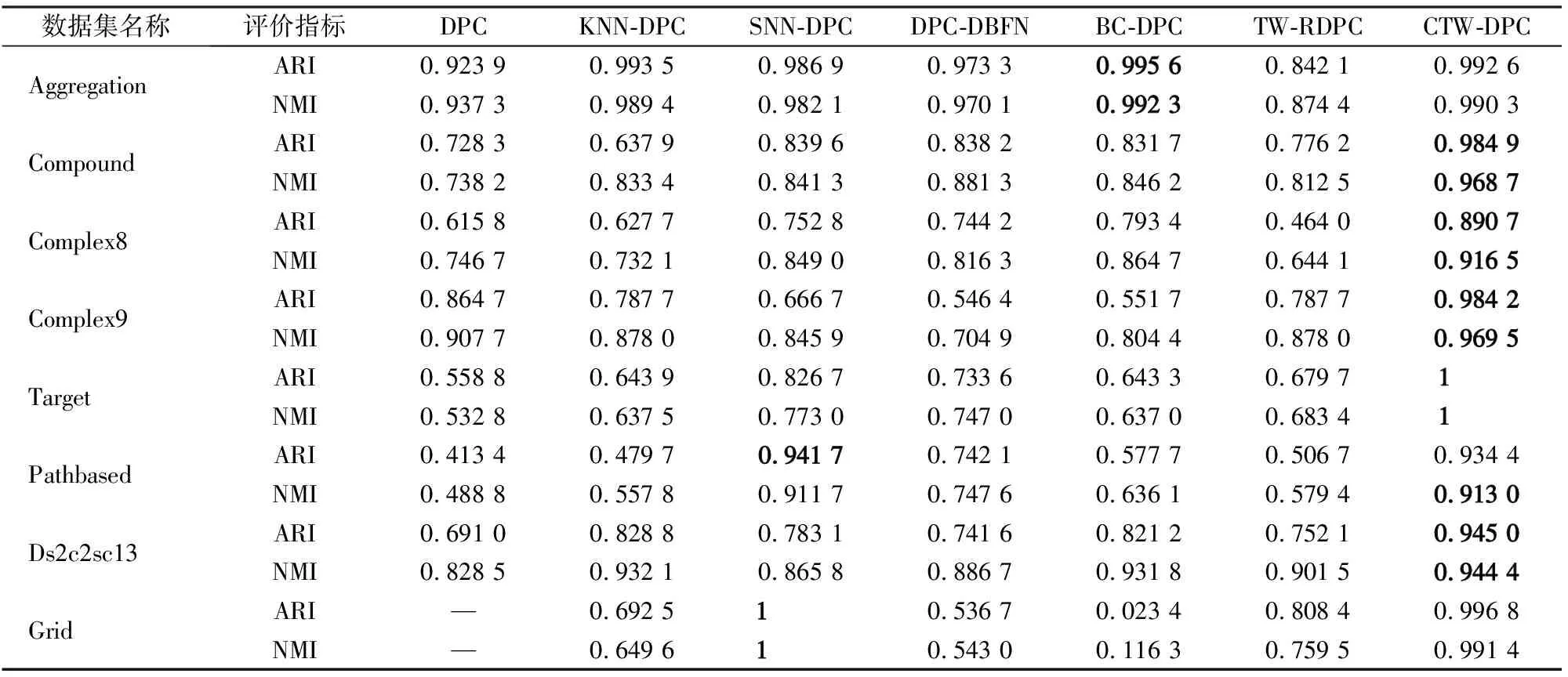
表5 人工数据集实验结果

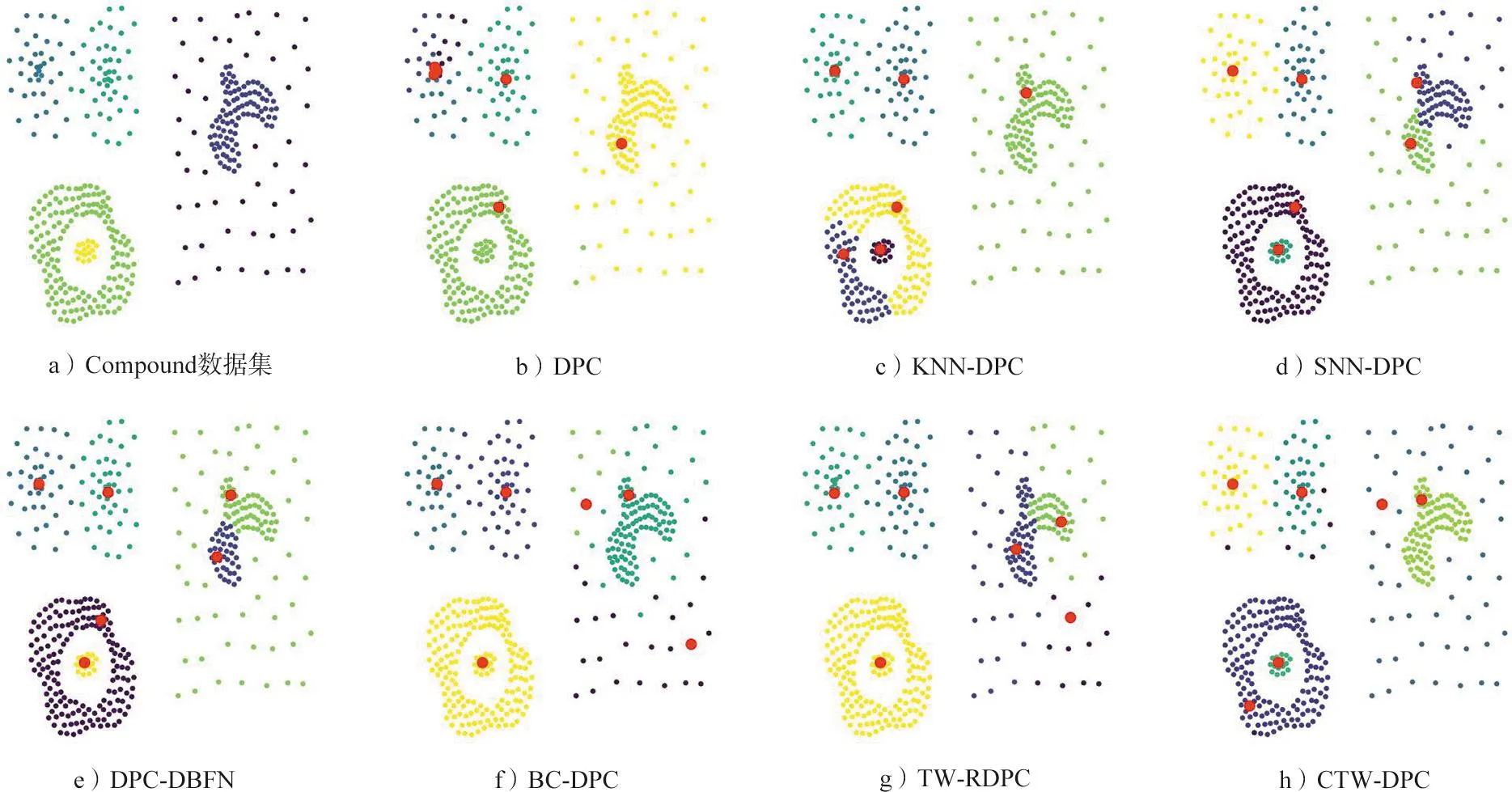
图4 不同算法聚类结果比较图

图4中红点表示聚类中心,可以明显看出只有CTW-DPC找到了所有的簇,且没有出现误分配的问题,其余算法皆出现了误分配的问题。DPC,KNN-DPC,SNN-DPC和DPC-DBFN均未能找到低密度的簇。BC-DPC与TW-RDPC因较好的密度函数定义,找到了低密度的簇,但仍没能避免同一个簇中出现2个密度峰值点的情况,但本文提出的算法很好地解决了该问题。

3.2 真实数据集上的实验结果

表6所呈现的结果为7种算法在10种真实数据集上的数值表现。虽然CTW-DPC在一些数据集上的表现未能超越之前的算法,但其总体表现稳定,与最优算法的评价指标相差不大,尤其是在Waveform和Heart数据集上较其他算法有了明显的提升。此外,对于多类别的手写数字图像集Opt digits和Pendigits,本文提出的算法也有良好表现。

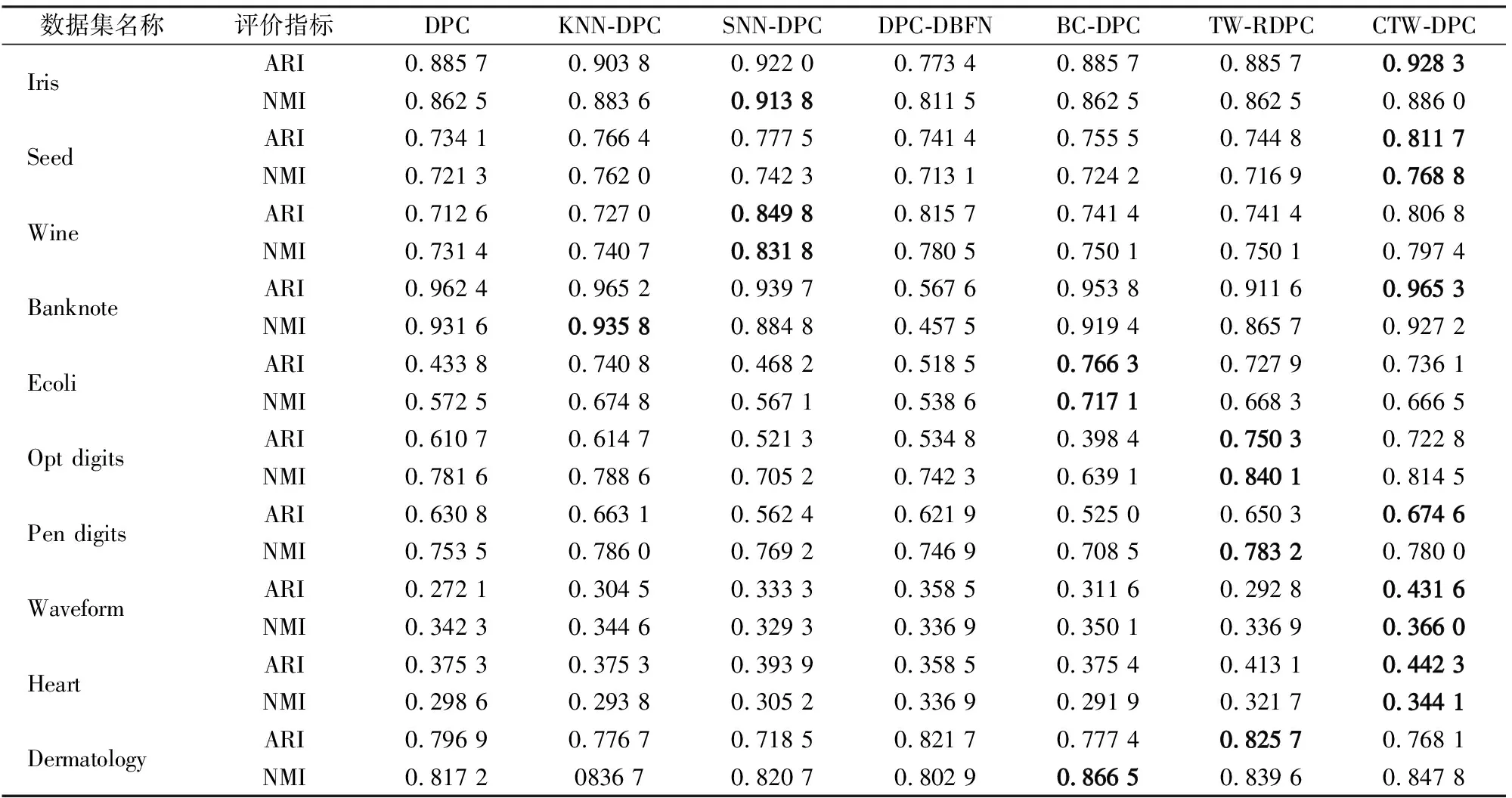
表6 真实数据集实验结果

但需注意的是,包括本算法在内的这类密度峰值聚类算法,在真实数据集上的表现多数情况下劣于传统的K-means聚类算法和谱聚类算法。这是因为在真实数据集中,不同类别的样本往往会在边界处有重合部分,使得该重合边界在流形上是连通且密度较高的,导致出现误分配以及错误选择密度峰值点的问题。

4 结 语

本文提出的基于连通性的三支密度峰值聚类算法,可以有效解决密度峰值聚类中低密度聚类难以被发现和误分配的问题。通过利用三支边界域的良好数学性质并引入连通性的概念,将原本属于同一正域的样本点进行合并,既避免了复杂计算,又能更好地反映簇间的关系,对于处理大规模流形数据提供了有价值的解决方案。

本文以参数形式给出的连通性有着较大的敏感度,对于不同的数据集需要进行调参,因而会造成时间以及计算资源的浪费。未来将引入连通性和连通度的概念对算法进行改进和优化。

参考文献/References：

[1] XU Rui,WUNSCH D.Survey of clustering algorithms[J].IEEE Transactions on Neural Networks,2005,16(3):645-678.

[2] DONG Guo,XIE Ming.Color clustering and learning for image segmentation based on neural networks[J].IEEE Transactions on Neural Networks,2005,16(4):925-936.

[3] LU Mei,ZHAO Xiangjun,ZHANG Li,et al.Semi-supervised concept factorization for document clustering[J].Information Sciences,2016,331:86-98.

[4] TRUONG H Q,NGO L T,PEDRYCZ W.Granular fuzzy possibilistic C-means clustering approach to DNA microarray problem[J].Knowledge-Based Systems,2017,133:53-65.

[5] JIAO Pengfei,YU Wei,WANG Wenjun,et al.Exploring temporal community structure and constant evolutionary pattern hiding in dynamic networks[J].Neurocomputing,2018,314:224-233.

[6] RODRIGUEZ A,LAIO A.Clustering by fast search and find of density peaks[J].Science,2014,344(6191):1492-1496.

[7] XIE Juanying,GAO Hongchao,XIE Weixin,et al.Robust clustering by detecting density peaks and assigning points based on fuzzy weighted K-nearest neighbors[J].Information Sciences,2016,354:19-40.

[8] DU Mingjing,DING Shifei,JIA Hongjie.Study on density peaks clustering based on K-nearest neighbors and principal component analysis[J].Knowledge-Based Systems,2016,99:135-145.

[9] LIU Rui,WANG Hong,YU Xiaomei.Shared-nearest-neighbor-based clustering by fast search and find of density peaks[J].Information Sciences,2018,450:200-226.

[10] ZHANG Qinghua,DAI Yongyang,WANG Guoyin.Density peaks clustering based on balance density and connectivity[J].Pattern Recognition,2023,134.DOI:10.1016/j.patcog.2022.109052.

[11] 马春来,单洪,马涛.一种基于簇中心点自动选择策略的密度峰值聚类算法[J].计算机科学,2016,43(7):255-258.

MA Chunlai,SHAN Hong,MA Tao.Improved density peaks based clustering algorithm with strategy choosing cluster center automati-cally[J].Computer Science,2016,43(7):255-258.

[12] LOTFI A,MORADI P,BEIGY H.Density peaks clustering based on density backbone and fuzzy neighborhood[J].Pattern Recognition,2020.DOI:10.1016/j.patcog.2020.107449.

[13] CHENG Dongdong,HUANG Jinlong,ZHANG Sulan,et al.K-means clustering with natural density peaks for discovering arbitrary-shaped clusters[J].IEEE Transactions on Neural Networks and Learning Systems,2023.DOI:10.1109/TNNLS.2023.3248064.

[14] SUN Chen,DU Mingjing,SUN Jiarui,et al.A three-way clustering method based on improved density peaks algorithm and boundary detection graph[J].International Journal of Approximate Reasoning,2023,153:239-257.

[15] BEZDEK J C,EHRLICH R,FULL W.FCM:The fuzzy C-means clustering algorithm[J].Computers &Geosciences,1984,10(2/3):191-203.

[16] 祖志文,李秦.基于马氏距离的模糊聚类优化算法——KM-FCM[J].河北科技大学学报,2018,39(2):159-165.

ZU Zhiwen,LI Qin.KM-FCM:A fuzzy clustering optimization algorithm based on Mahalanobis distance[J].Journal of Hebei University of Science and Technology,2018,39(2):159-165.

[17] LINGRAS P,WEST C.Interval set clustering of web users with rough K-means[J].Journal of Intelligent Information Systems,2004,23(1):5-16.

[18] 姚一豫,祁建军,魏玲.基于三支决策的形式概念分析、粗糙集与粒计算[J].西北大学学报(自然科学版),2018,48(4):477-487.

YAO Yiyu,QI Jianjun,WEI Ling.Formal concept analysis,rough set analysis and granular computing based on three-way decisions[J].Journal of Northwest University(Natural Science Edition),2018,48(4):477-487.

[19] YAO Yiyu.Three-way decisions with probabilistic rough sets[J].Information Sciences,2010,180(3):341-353.

[20] YU Hong.A framework of three-way cluster analysis[C]//International Joint Conference on Rough Sets.Olsztyn:Springer,2017:300-312.

[21] WANG Pingxin,YAO Yiyu.CE3:A three-way clustering method based on mathematical morphology[J].Knowledge-Based Systems,2018,155:54-65.

[22] BRYANT A,CIOS K.RNN-DBSCAN:A density-based clustering algorithm using reverse nearest neighbor density estimates[J].IEEE Transactions on Knowledge and Data Engineering,2018,30(6):1109-1121.

[23] BENTLEY J L.Multidimensional binary search trees used for associative searching[J].Communications of the ACM,1975,18(9):509-517.