非接触式回转体测量系统的路径规划
韩佳昊,王武 , ,贡乐凯,柏中树,
(1. 长春理工大学 光电工程学院,长春 130022;2. 北方导航控制技术股份有限公司,北京 100176;3. 长春新产业光电技术有限公司,长春 130103)
非接触式测量方法是近年来工件三维尺寸测量的发展趋势。 对于非接触式位移量测量,激光位移传感器是一种广泛应用的形式[1-3],对于测量机械运动平台,三坐标测量技术柔性好,也能适应高节拍生产要求[4-6]。非接触测量技术与三坐标测量技术相结合,具有测量效率高、避免与被测工件接触等优点[7-9]。
目前,在非接触式测量过程中,常用的路径规划方法有以下几种:基于蚁群算法的路径规划方法、基于Dijkstra 算法的路径规划方法、曲面三角形自适应测量方法等[10]。
王禹等人[11]建立了以BP(Back Propagation)神经网络为基础的路径规划模型,使路径拟合与预测的精确性、高效性得到了很好的提高;此外,许多学者对坐标测量机的检测路径进行优化,如蚁群算法、遗传算法和粒子群算法等,通过对比分析,更好地提高了系统对路径优化的效率[12-13];Miao 等人[14]利用蚁群算法进行多目标优化,把路径长度、安全性综合考虑,利用自适应改进蚁群算法得出多目标的最优路径;张恒等人[15]将蚁群划分为引导层蚁群和普通层蚁群,降低了算法在迭代过程中陷入局部最优的可能。 尽管上述文献已对路径规划有众多研究,但在非接触式坐标测量方面仍有欠缺。
基于以激光位移传感器作为测头的三坐标测量系统,针对带有多个台阶面的回转体测量过程中的路径规划进行研究,从测量精度和测量效率两个方面分析测量路径优化的方法。
1 非接触式三坐标测量原理
1.1 系统结构组成
针对带有多个台阶面,直径在100~400 mm之间的回转体测量,回转体中最大直径和最小直径的差值为100 mm。非接触测量系统以激光三角测量原理为基础,通过激光在工件表面反射光产生触发信号,这种非接触测量方式效率高、无磨损、采样快、灵活性更高。
测量系统如图1 所示,运动机构包括三维坐标移动平台以及高精度转台,由激光采集测头到工件表面的距离,光栅尺采集三维坐标移动平台的移动数据,采集后的数据经上位机处理系统进行拟合得到测量结果。 通过尺寸规划,系统采用非接触式测头,测头的作用距离为150 mm,量程±5 mm,激光测头的量程有限,所以通过三维坐标移动平台带动测头运动,转台带动工件旋转的方法,实现被测工件表面位置的数据采集,再由上位机对采集的数据进行处理,实现对回转体工件的尺寸测量。
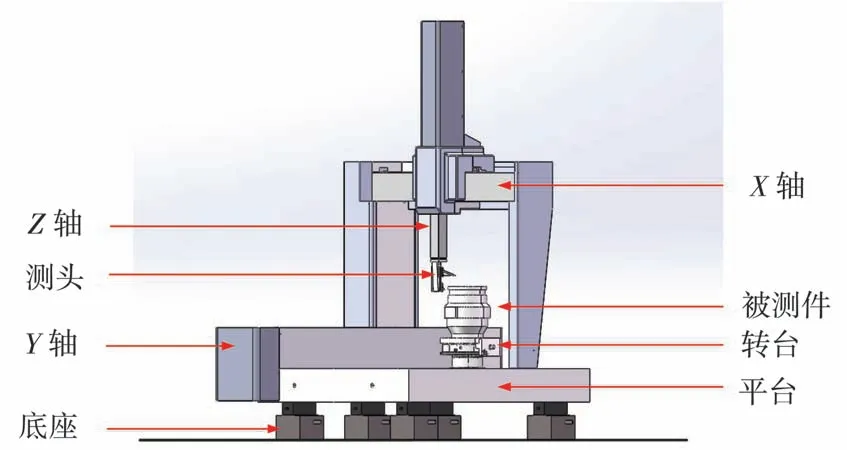
图1 测量系统结构示意图
1.2 测量原理
如图2 所示,在测量过程中,被测件被固定在高精度转台上,三坐标带动非接触式测头,让第一个被测点置于测头的测量范围中,然后开始旋转转台,逐个截面进行扫描测量,在扫描过程中,同时记录测头读数d、测头在空间中的位置(x,y,z)、和旋转的角度r,三者记录测量信息的时间轴保持一致,最后由同一时刻三个测量信息经数据拟合得到完整的工件某截面的径向尺寸R。
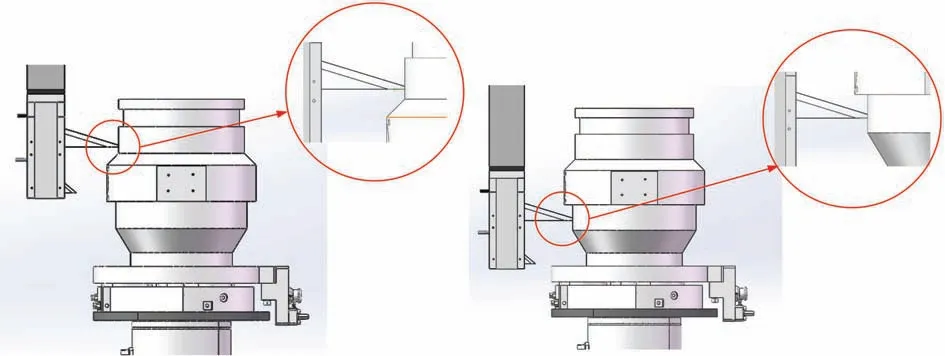
图2 测量系统工作原理示意图
由于测头的量程有限,需合理设置测头空间位置x、y以保证测头能够采集到有效数据,因此测头的运动路径会直接影响系统的测量结果。
同时采样点的采样顺序也会对测量效率产生影响,若采样点的采样顺序不够合理,使测头的运动路径过于复杂,增加测头运动路径长度,增加测头运动的往返次数,从而产生冗余路径,影响采样值,进而影响最终的测量效率。
基于上述测量原理的系统,对测头的运动路径进行规划,对采样点的采样顺序进行选择,缩短测头的运动路径,减少测头运动的往返次数,能够有效减少测量过程中由测头运动带来的误差,可有效提高测量效率和测量精度。
2 路径规划算法研究
由于三维移动平台产生的冗余路径会对测量精度产生影响,如果减少冗余路径就需要减少三维移动平台的往复运动,可以通过规划采样点的采样顺序达到这一目的。在采样过程中还需保证采样点在测头的信号触发范围内,同时考虑避障问题。为寻找到一条可以保证精度且安全的路径,采用蚁群算法对系统的测量路径进行规划。
蚁群算法[16]是用于寻找最优路径的概率型算法。 蚁群算法灵感来源于蚂蚁的觅食过程,蚂蚁在觅食过程中,为供后面的蚂蚁判断路径,会在经过的路径留下信息素。为解决旅行商问题、指派问题、图着色问题等问题,蚁群算法经常与其他算法组合应用。
本文用旅行商问题解决采样点规划,对于旅行商问题,建立蚁群算法模型,具体步骤如图3所示。
蚁群算法中,参数影响蚁群算法的效率和收敛速度,通过蚁群算法进行路径规划实验,找到最适应本测量系统的参数,得到测量效率最高、测量精度最高的算法参数。
其中,α启发因子的值越大,下一只蚂蚁越有可能选择上一只蚂蚁走过的路径,使搜索路径的随机性减弱,而α值减小,蚁群算法的搜索范围会减小,从而使算法易陷入局部最优。β期望因子的值升高,容易使蚁群算法陷入局部最优、随机性降低的状态,从而使蚁群算法的收敛速度加快。ρ信息素残留浓度过小时,路径上信息素挥发速度减慢,导致蚂蚁在路径上留下过多的信息素,使无效路径被重复搜索,使算法的收敛速度降低。ρ过大时,无效路径被轻松排除,但会忽略部分有效路径,从而影响算法的最优结果。合适的蚂蚁数量对算法运行时间有重要影响,m数目越多,越容易得到更精确的最优解,但会产生无用重复解,增加重复工作,增加算法运行时间。q为总的信息素。
2.1 启发因子和期望因子的设定
蚁群算法中的启发因子α与蚂蚁移动时所经之处留下的信息素相似,这些信息素可以在蚂蚁经过时叠加,也可以在蚂蚁离开时挥发。在这一过程中,采样点之间的距离会影响蚂蚁的转移过程,将采样点的距离在蚂蚁采样过程中的重要程度设为期望因子β。 通过实验对启发因子α与期望因子β对蚁群算法的影响进行分析。设置30 个采样点,设信息素残留参数ρ=0.5,蚂蚁数量m=30,总的信息素Q=100,选取不同的启发因子α和期望因子β值进行比较。
图4 中,横坐标表示启发因子α,纵坐标表示路径长度,当启发因子α由0.1 增大至1 时,路径不断缩短,当α超过1 并逐渐增大时,路径不断增加。 图5 中,横坐标表示启发因子α,纵坐标表示迭代次数。随着启发因子α不断增大,迭代次数不断减少,当启发因子α到2 时,迭代次数达到最小值,且随着启发因子α增加,迭代次数不再减少。
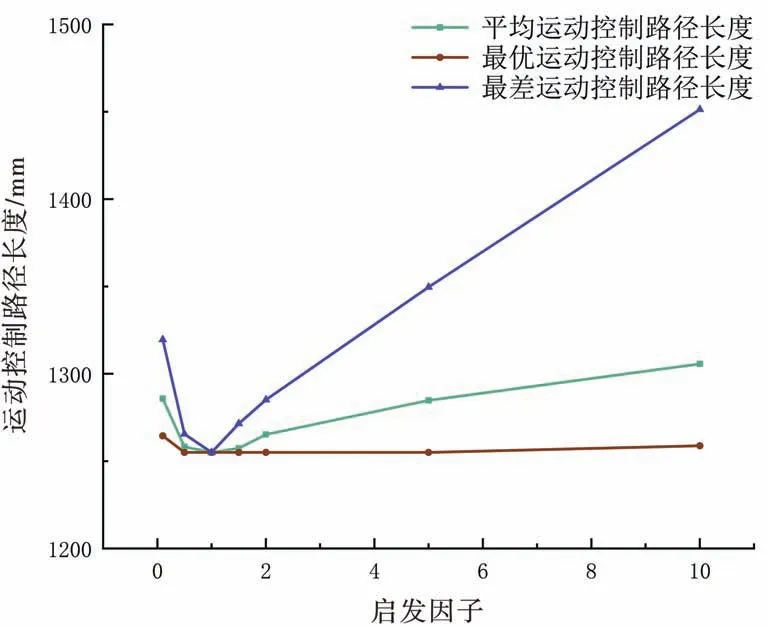
图4 不同启发因子对路径的影响
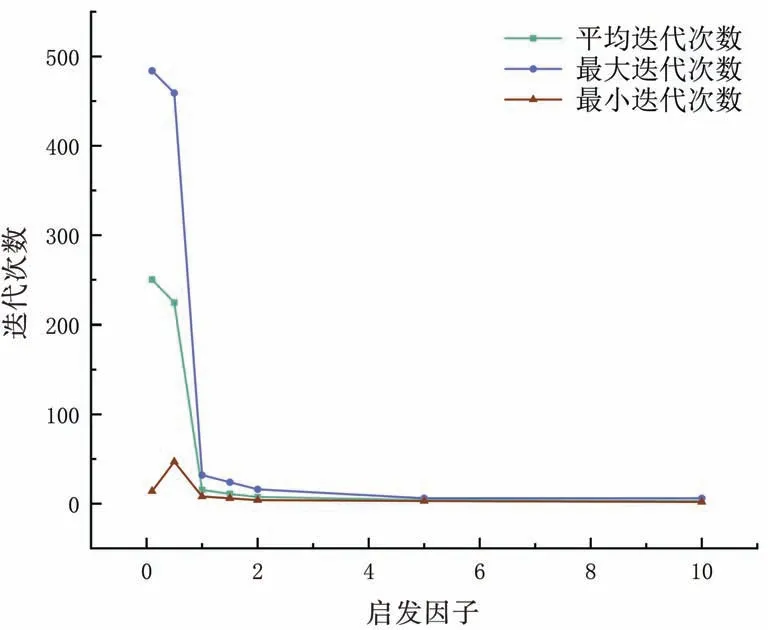
图5 不同启发因子对迭代次数的影响
当启发因子α取值过小时,使蚁群算法中的信息素浓度不够重视,算法的搜索结果差,不会过早停滞,很难找到最优解;反之,当启发因子α取值过大时,又使蚁群算法在搜索过程中对信息素浓度产生过分依赖,容易产生局部最优解;选取合适的启发因子α值,蚁群算法的搜索质量高,收敛速度快,且算法稳定,综上启发因子α取值1~1.5 最佳。
图6 中,横坐标表示期望因子β,纵坐标表示路径长度,随着期望因子β不断增大,路径不断缩短,当期望因子β到1 时,路径达到最短,且随着期望因子β增加路径不再减少。图7 中,横坐标表示期望因子β,纵坐标表示迭代次数。当期望因子β从0.1 增大至1.5 时,迭代次数不断减少,当超过1.5 逐渐增大时,迭代次数不断增加,当期望因子β超过1.5 时,迭代次数不断减少,当期望因子β为10 时达到最小值。
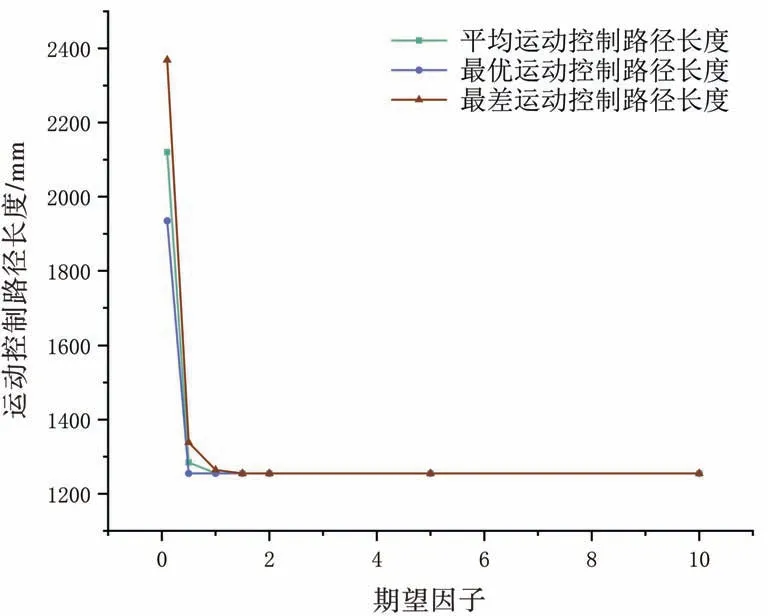
图6 不同期望因子对路径的影响
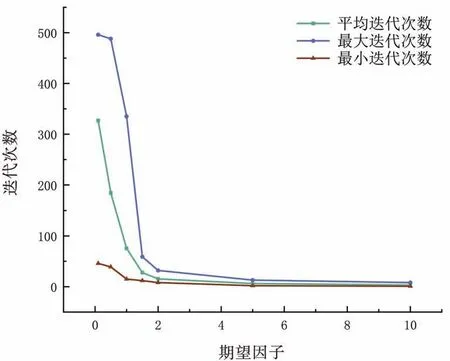
图7 不同期望因子对迭代次数的影响
当对于期望因子β选取值过小时,蚂蚁在搜索路径过程中缺乏方向感,算法不会过早停滞,搜索结果差,容易陷入局部循环,很难找到最优解;反之,期望因子β选取值过大时,算法会过早停滞,搜索结果差,使蚁群算法在搜索过程中陷入局部最优解。当选取合适的期望因子β值时,蚁群算法的搜索质量会很高,且收敛速度适中,算法稳定,经分析得出期望因子β取值为2~10 最佳。
2.2 信息素残留系数的设定
在蚁群算法中,信息素的残留系数ρ表示蚂蚁在运动过程中释放的信息素,信息素可以随着该路径上经过的蚂蚁数逐渐增加,也会随着时间逐渐挥发,信息素的挥发系数为1~ρ。当ρ取不同数值时,对蚁群算法的影响是不同的。在此处共设置30 个采样点,设置启发因子α=1.0,期望因子β=4.0,总的信息素Q=100,蚂蚁数量m=40,选取不同的信息素的残留系数ρ值进行比较。
信息素的残留系数ρ分别取0.1、0.3、0.5 和0.7,每组数据重复进行20 次测试。图8 中,横坐标表示信息素的残留系数ρ,纵坐标表示路径长度,随着期望因子β不断增大,最优路径与平均路径略有缩短,最差路径波动较大;图9 中,横坐标表示信息素的残留系数ρ,纵坐标表示迭代次数。当信息素的残留系数ρ从0.1 增大至0.5 时,迭代次数比较平稳,当超过0.5 逐渐增大时,最大迭代次数突然减少。
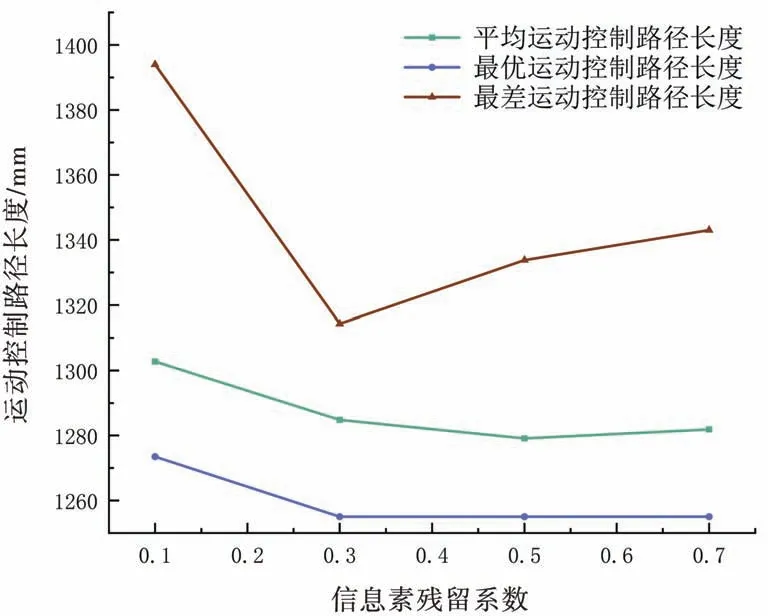
图8 信息素残留系数对路径的影响
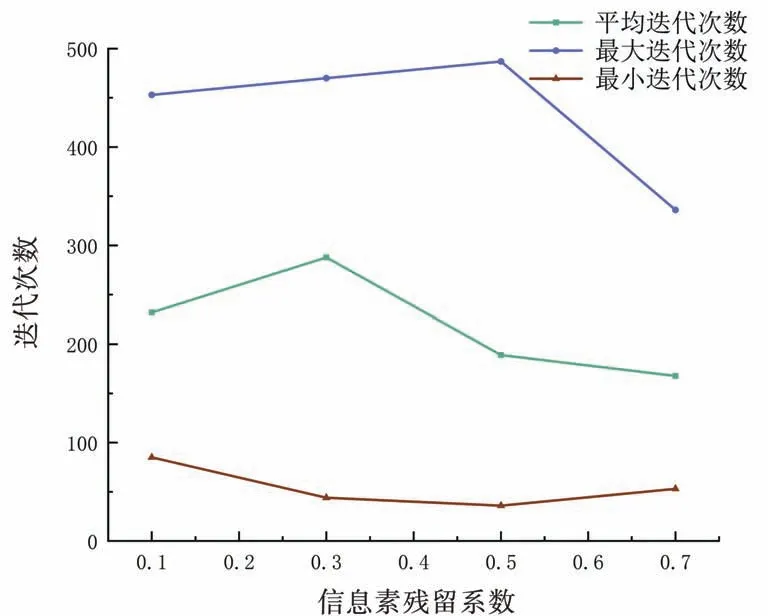
图9 信息素残留系数对迭代次数的影响
对实验结果进行分析,在其他参数不变的情况下,蚁群算法受信息素残留系数ρ影响较大,其取值较小时,在蚁群算法中起主导作用是正反馈机制,容易使蚁群算法陷入局部最优解,当信息素的残留系数ρ取值较大时,蚁群算法的收敛速度减慢,但全局搜索能力得到改善,综上,信息素的残留系数ρ的取值0.5~0.7 为最佳。
2.3 蚂蚁数量m 的设定
蚂蚁之间的交流对算法也起着至关重要的作用,用m表示蚁群算法中蚂蚁的数量,如果所有蚂蚁协调起来,就会让算法变得井然有序,避免出现错综复杂的情况。 算法在运行过程中,每只蚂蚁选择的路径都不一样,这些路径的集合就是一个解集。 与此同时,算法解集的规模受蚂蚁数量的影响。为了得到一个合适的蚂蚁数量,选取30 个采样点,设置启发因子α=1,总的信息素Q=100,期望因子β=4.0,信息素残留系数ρ=0.5,进行实验以获得合适的蚂蚁数量。
图10 中,横坐标表示蚂蚁数量m,纵坐标表示路径长度,随着蚂蚁数量m不断增加,路径长度不断减少,当蚂蚁数量达到70 时,逐渐趋于平稳,蚂蚁数量达到90 时,随着数量的增加,迭代次数突然产生波动,后趋于平稳;图11 中,横坐标表示蚂蚁数量m,纵坐标表示迭代次数,当蚂蚁数量m逐渐增加时,迭代次数逐渐减小,超过70 时,迭代次数出现大幅度波动。
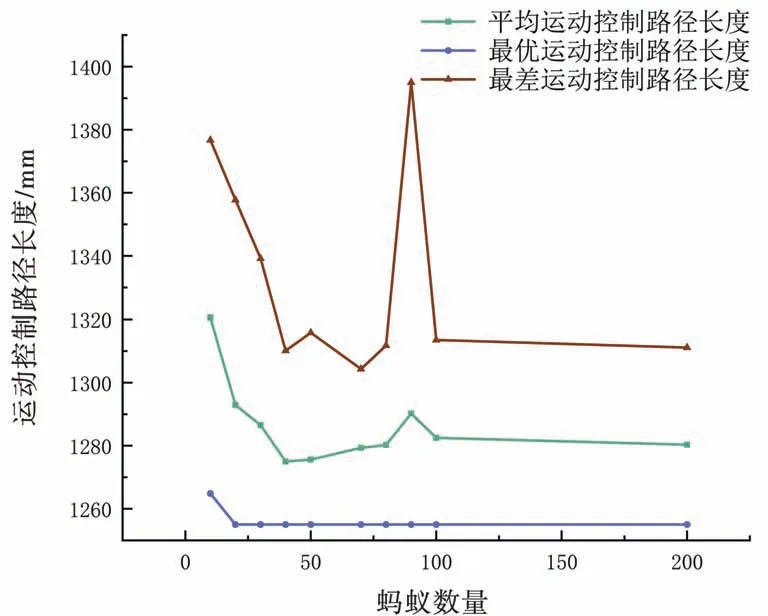
图10 蚂蚁数量m 对路径的影响
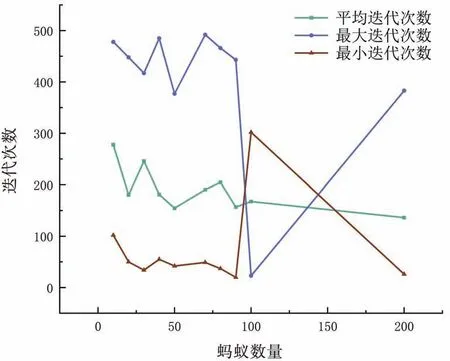
图11 蚂蚁数量m 对迭代次数的影响
蚁群算法的搜索结果在蚂蚁数量较少时达不到理想要求,随着蚂蚁数量的增加,蚁群算法的搜索结果得到改善,但是蚁群算法中的解集规模与蚂蚁数量成正比。 蚂蚁数量取值越大,算法的搜索结果越理想,但需要花费更多的时间来进行算法的迭代;相反,如果蚂蚁数量取值越小,算法收敛速度越快,迭代时间越少,但算法的稳定性就越低,全局搜索能力越差。综上,蚂蚁数量m取值40~80 最佳。
2.4 总的信息素的设定
总的信息素Q表示蚁群算法中蚂蚁在一个周期释放的所有信息素,Q是一个固定值。为了验证总的信息素在蚁群算法中的重要性,根据上述实验得到最理想的参数,并且依旧选择30个采样点,设置启发因子α=1,蚂蚁数量m=45,期望因子β=4,信息素残留系数ρ=0.5,进行实验。
图12 中,横坐标表示总的信息素Q,纵坐标表示路径长度,随着总的信息素Q不断增大,路径长度的变化逐渐趋于平稳,且当总的信息素Q达到60 时,路径长度几乎不随总的信息素Q的变化而变化;图13 中,横坐标表示总的信息素Q,纵坐标表示算法迭代次数,当总的信息素Q增大时,算法的迭代次数减小,总的信息素Q为60 时,最大迭代次数的值增大,Q为100 时达到最大值,后逐渐减少并趋于平稳。
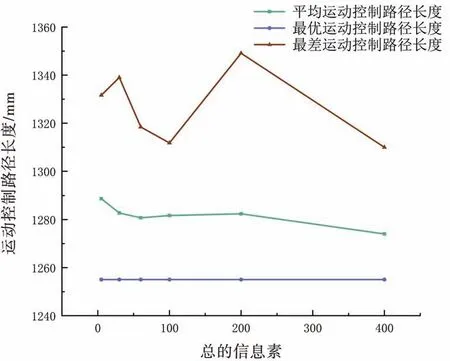
图12 总的信息素对路径的影响
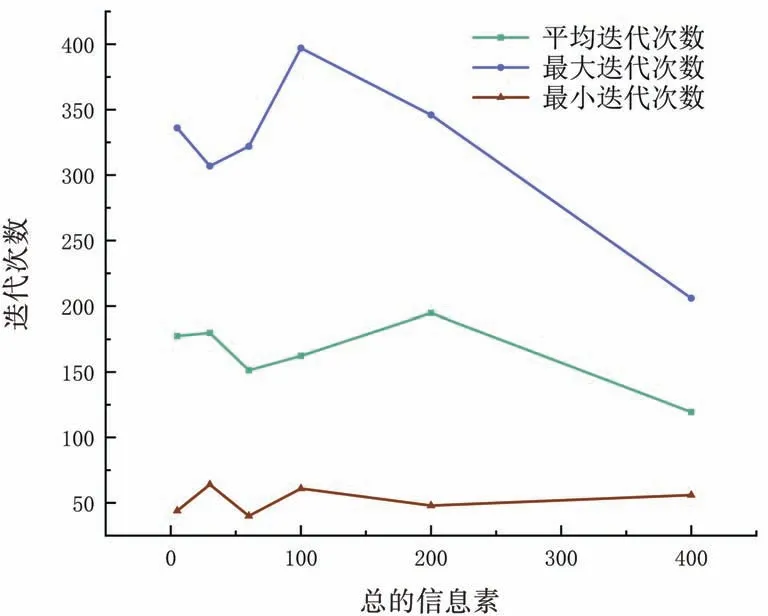
图13 总的信息素对迭代次数的影响
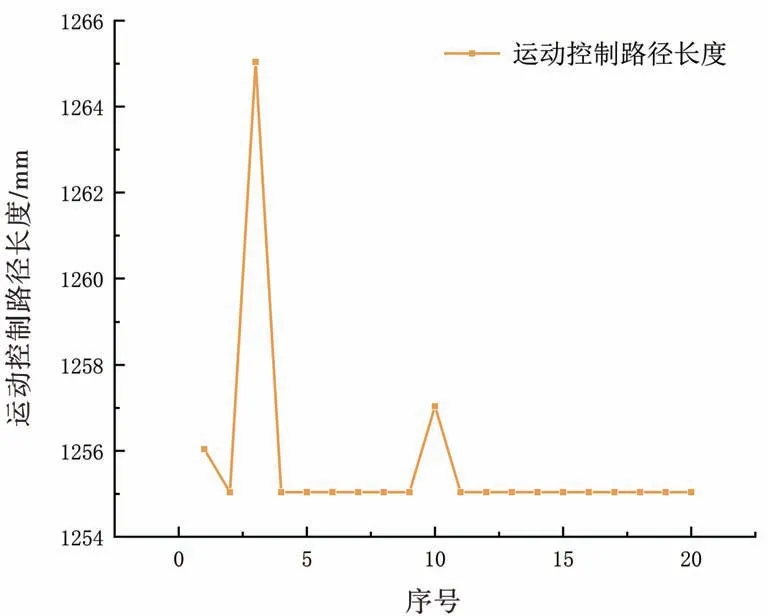
图14 最优结果
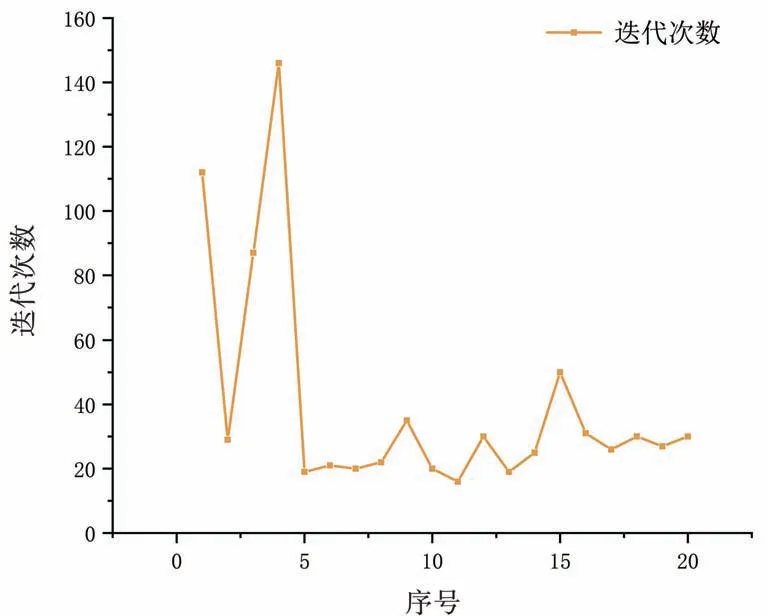
图15 迭代次数
根据实验结果,总的信息素的值对实验结果的影响很小,蚁群算法的收敛速度随总的信息素减小而减慢,综上总的信息素Q的取值30~100最佳,使算法能够快速收敛并得到最优解。
3 路径优化综合实验
对上述所有实验参数进行整合,得出最佳参数进行实验,最终选取启发因子α=1,期望因子β=4.0,蚂蚁总数m=50,总的信息素Q=100,信息素残留系数ρ=0.5,进行20 组实验,对实验结果比较分析。
最优路径的平均值1 255.690 6 mm,最小值1 255.040 6 mm,最大值1 265.040 6 mm,全局搜索能力强,搜索质量高,算法稳定性强;平均迭代次数29.1 次,最大迭代次数193 次,最小迭代次数7 次,收敛速度适中。综上,通过对启发因子、期望因子、信息素残留系数、蚂蚁总数、总的信息素Q的研究,得出了一组比较可靠的参数。
对于回转体测量规划实例,首先获取测量特征,获取采样点数量为30 个。其分布情况如图16 所示。
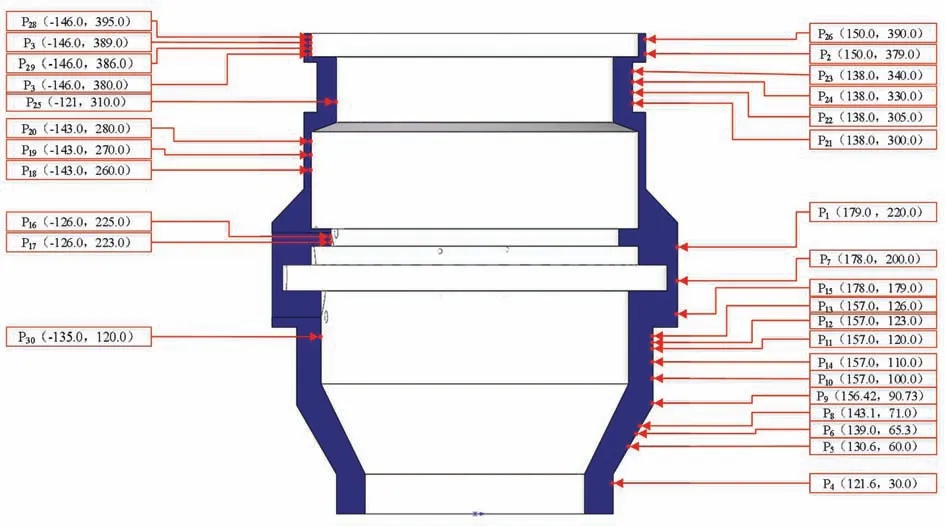
图16 测量点分布
根据被测特征,在采用蚁群算法前对采样路径进行规划,采样点的采样顺序为P25→P28→P26→P24→P10→P1→P5→P11→P13→P12→P6→P14→P4→P30→P22→P21→P2→P15→P7→P9→P8→P23→P17→P19→P27→P3→P16→P20→P18→P29→P25。 测 量 顺序图如图17 所示,在此测量路径下测量完成一个工件所需测量时间约35 min,测头的运动路径长度3 502.808 7 mm。
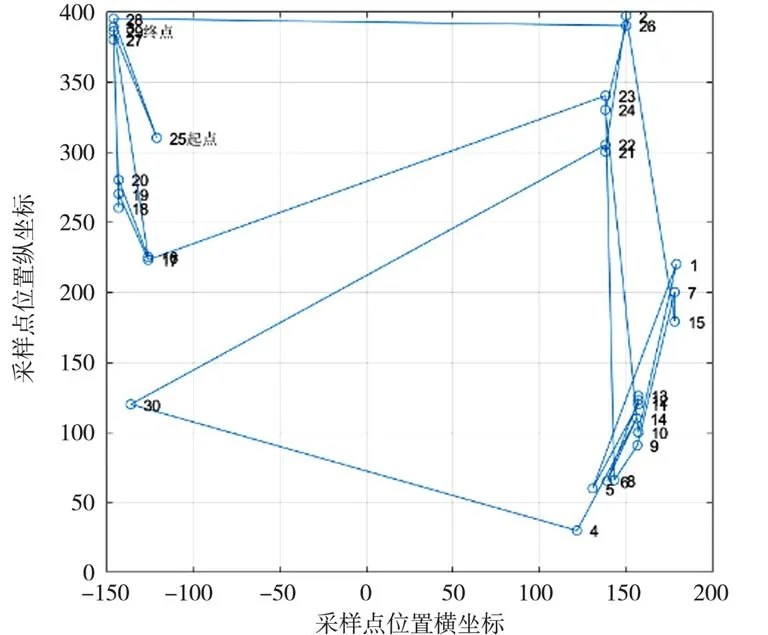
图17 路径规划前采样顺序图
利用蚁群算法对采样点的采样顺序进行规划,得到采样顺序结果:P30→P17→P16→P18→P19→P20→P25→P27→P29→P3→P28→P2→P26→P23→P24→P22→P21→P1→P7→P15→P13→P12→P11→P14→P10→P9→P8→P6→P5→P4→P30。采样顺序图如图18 所示,在此测量路径下测量完成一个工件所需测量时间约30 min,测头的运动路径长度1 255.406 mm,算法运行时间15.36 s。
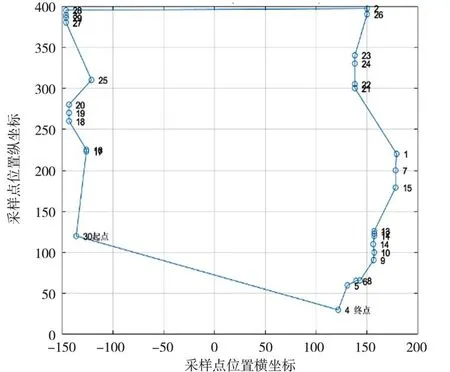
图18 优化后采样顺序图
通过采样点测量顺序进行规划前后实验结果对比,经蚁群算法对采样点的采样顺序进行优化后,测量时间节省了约5 min,测头的运动路径减少了2 247.402 7 mm,由图17 与图18 对比可得测头运动往返次数明显减少。
经过系统理论的仿真分析后,在实际应用中进行实验验证。首先搭建实验平台,如图19 所示。

图19 非接触式测量系统实验平台
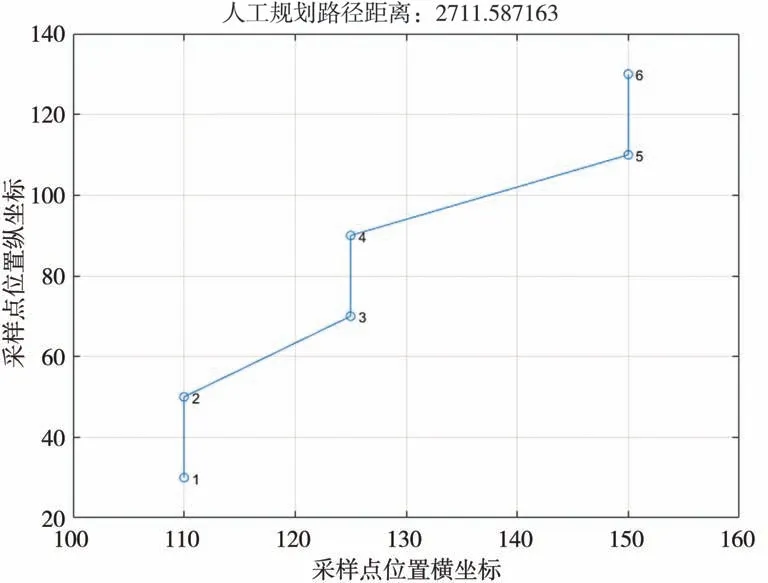
图20 蚁群算法路径规划采样顺序图
图中包括150 mm 测头、三维移动平台以及转台。利用本文的蚁群算法规划的路径进行采样,对标准样柱进行测量,将所得到的采样点数据进行拟合,验证系统的测量精度。
根据图21、图22、图23 的实验结果分析,对回转体零件的测量精度实现5 µm 以内,测量结果稳定,接近真实值。
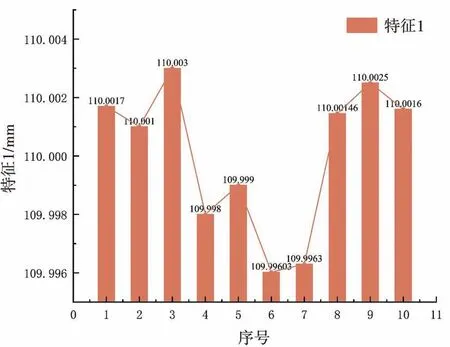
图21 特征1 测量尺寸
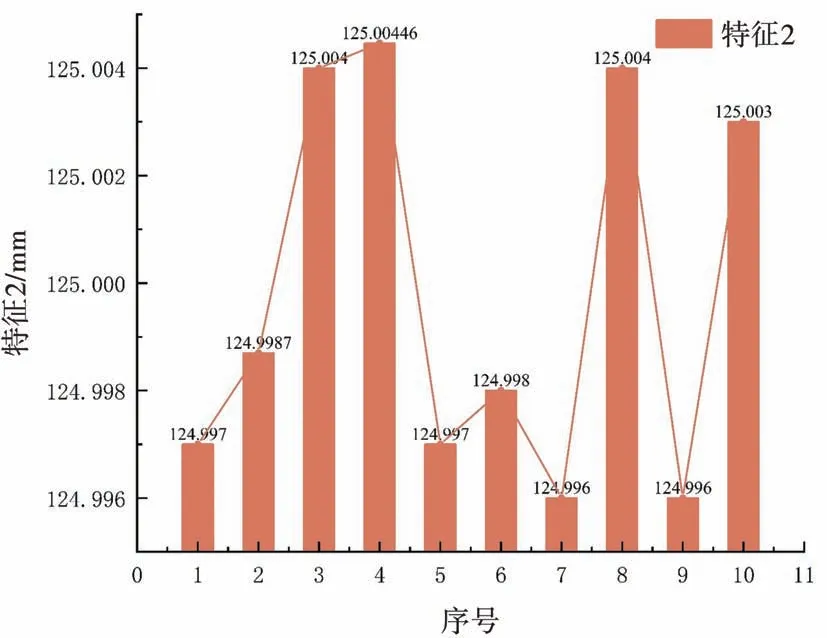
图22 特征2 测量尺寸
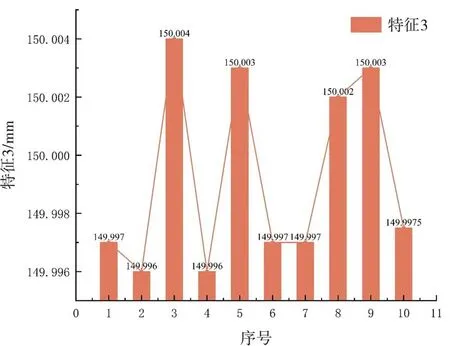
图23 特征3 测量尺寸
综合以上实验,通过蚁群算法对路径进行规划,使测量系统的测量效率得到了有效的提升,测量时间减少,测头运动路径缩短,且系统的测量精度在5 µm 以内,测量结果稳定,达到预期要求。
4 结论
对于三维尺寸大于200 mm 的零件的测量,提出一种基于激光三角法的非接触式测量系统,分析对系统测量结果产生影响的因素,并对路径对系统的测量结果影响进行研究,通过蚁群算法对系统的运动路径进行规划,对采样点的采样顺序进行选择,缩短测头的运动路径,减少测头运动的往返次数,减少测量过程中由测头运动带来的误差,使测量效率和测量精度得到提高。 通过对蚁群算法的研究,最终设定启发因子α=1,期望因子β=4.0,信息素残留系数ρ=0.5,总的信息素Q=100,蚂蚁总数m=50。通过经蚁群算法规划前的实验结果与蚁群算法规划后的实验结果对比,验证经蚁群算法规划后的测量时间明显减少,测量路径明显缩短;对于设定的参数,通过实验进行验证,蚁群算法相对比较稳定,对于回转体零件的测量精度实现5 µm 以内,且测量结果相对稳定,接近真实值。 综上,经蚁群算法优化后,测量系统测量时间明显减少,测量路径明显缩短,有效地提高了系统的测量效率与测量精度。

