双腔磁振子系统的法诺共振及其快慢光传播

罗弋雄, 刘洪雨

( 延边大学 理学院, 吉林 延吉 133002 )

0 引言

研究显示,不同频率的光和物质在相互作用的过程中会产生一些独特的现象,如电磁诱导透明(EIT)[1]、光力诱导透明(OMIT)[2]、诱导放大[3]、光的相干操纵[4]和冷却[5-6]等.由于这些独特的现象在量子通信中具有重要作用,因此受到学者们的广泛关注．2018年,Li等[7]提出了一种在混合腔磁力系统中生成声子的方案．由于该方案所使用的铁磁性材料具有阻尼率低、自旋密度高,以及它与微波光子具有较强的协同性等优点,因此该方案为研究不同频率的光与物质的相互作用提供了一个良好平台．此外,一些学者还对基于腔磁力系统的磁力诱导透明(MMIT)、磁子诱导透明(MIT)[8]和双稳性[9]、磁子克尔效应[10]、贝尔非局域性[11]、快慢光传输[12-13]等量子现象进行了研究,并在实验上实现了腔磁力系统中的磁力诱导透明现象[14]．

法诺共振现象是一种在不同系统共振态之间产生的量子干涉现象．由于利用法诺共振的特殊线形特征可以对光学器件的频率进行精确选择和调控,以及利用法诺共振的干涉效应可以耦合和操控量子比特,因此近年来一些学者对其进行了研究[15-17]．基于上述研究,本文通过建立双腔磁力系统研究了不同子系统之间的耦合参数和腔磁耗散比对磁子诱导透明、磁力诱导透明、快慢光传输现象的影响,以及不同非共振参数下的法诺共振现象．

1 系统模型及其哈密顿

图1为混合双腔磁力系统模型的示意图及其等效模式的耦合模型.该模型由平行x轴的微波腔1、平行y轴的微波腔2和1个YIG球组成,其中YIG球位于两个正交微波腔场之间的中心,其直径为250 μm．该系统包含3种不同类型的激发,即光子、磁子和声子．YIG球中的磁子模由均匀的偏置磁场激活,同时被激活的磁子能够使YIG球发生几何形变而形成振动模(声子)．模型中,磁子模和微波腔通过磁偶极相互作用耦合,磁子模与声子通过磁致伸缩相互作用耦合.由于单个磁子的磁力耦合强度非常弱,因此本文通过对磁子施加外部微波驱动场来增强磁力耦合强度,同时采用一个弱的探测场驱动微波腔．

由于球的尺寸远小于微波波长,因此光子对声子作用产生的辐射压和磁子的克尔非线性对系统哈密顿量的影响可以忽略不计．由此得到的系统在旋波近似下的哈密顿量为:

(1)

(2)

其中:Δ1(Δ1=ω1-ωpu)、Δ2(Δ2=ω2-ωpu)和Δm(Δm=ωm-ωpu)分别为腔1、腔2和磁子的失谐;δ为探测场失谐,δ=ωpr-ωpu．系统中具有耗散和噪声的量子海森堡-朗之万方程为:

(3)

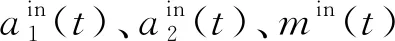
(4)

(iλ-κ1)a1+-ig1m++εpr=0, (iλ-κ2)a2+-ig2m+=0,

(iλ-κm)m+-ig1a1+-ig2a2+-iGb+=0, (iλ-κb)b+-iG*m+=0．

(5)

(6)

由腔场的输入输出关系(εout=εin-2κ1a1,εin和εout分别是输入场和输出场向量)[8]可得系统的输出场振幅为εout=2κ1a1+/εpr,其中实部Re[εout]=2κ1a1+/εpr(表示吸收),虚部Im[εout]=2κ1a1+/εpr(表示色散)．

由公式(εout=2κ1a1+/εpr)可知,探测场的透射与输出场振幅之间的关系可表示为tp=1-εout=1-2κ1a1+/εpr.由此可进一步得出输出场的相位变化为φτ=arg[εout],系统中群延迟的表达式为τg= ∂φτ/∂ωpr(其中群延迟的正(负)值表示光传输慢(快)的发生)．由这两个式子可知,输出场的相位变化是产生快慢光的原因．

2 双腔磁力系统的磁子诱导透明和磁力诱导透明现象

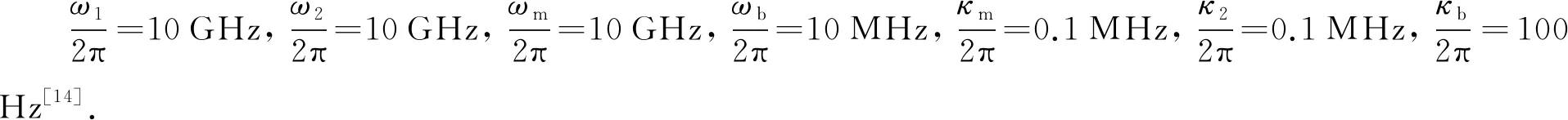
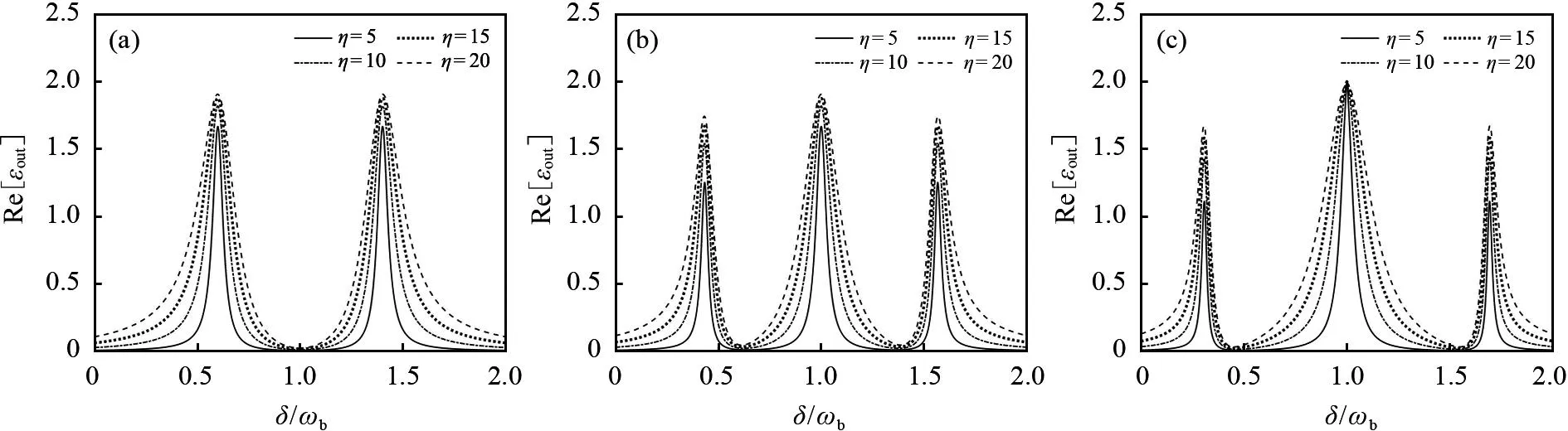
图2 不同腔1磁子耗散比(η)时吸收谱(Re[εout])与归一化探测场失谐(δ/ωb)的关系

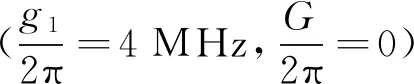
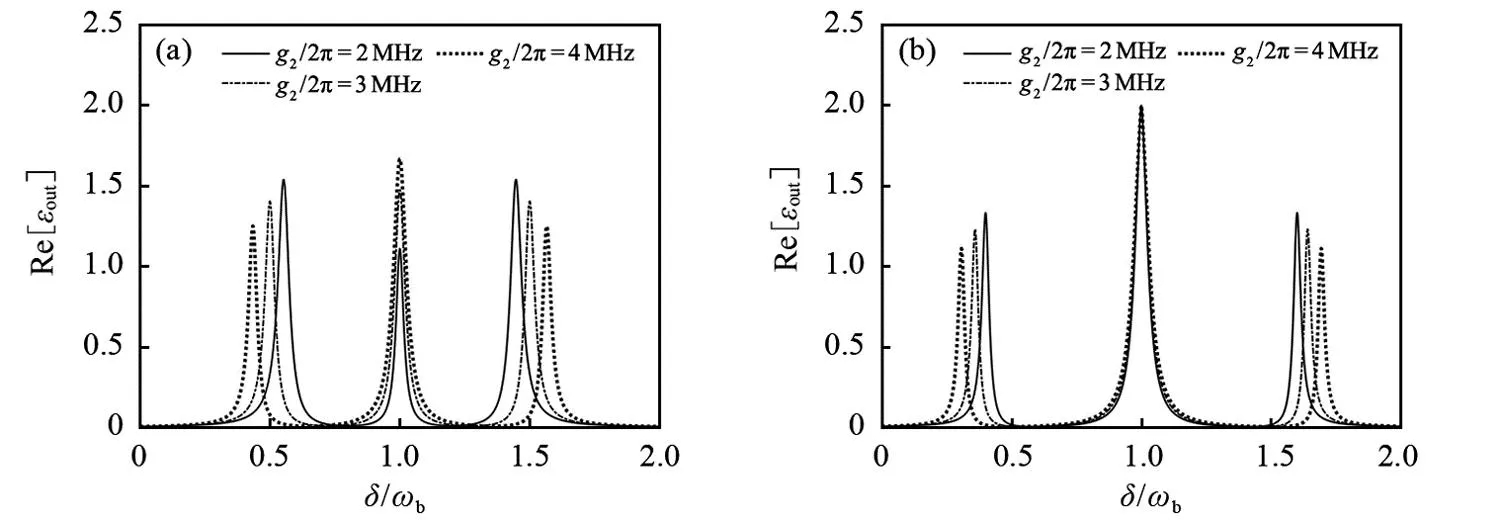
图3 不同腔2磁子耦合强度(g2)时吸收谱(Re[εout])与归一化探测场失谐(δ/ωb)的关系

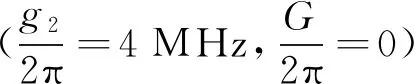
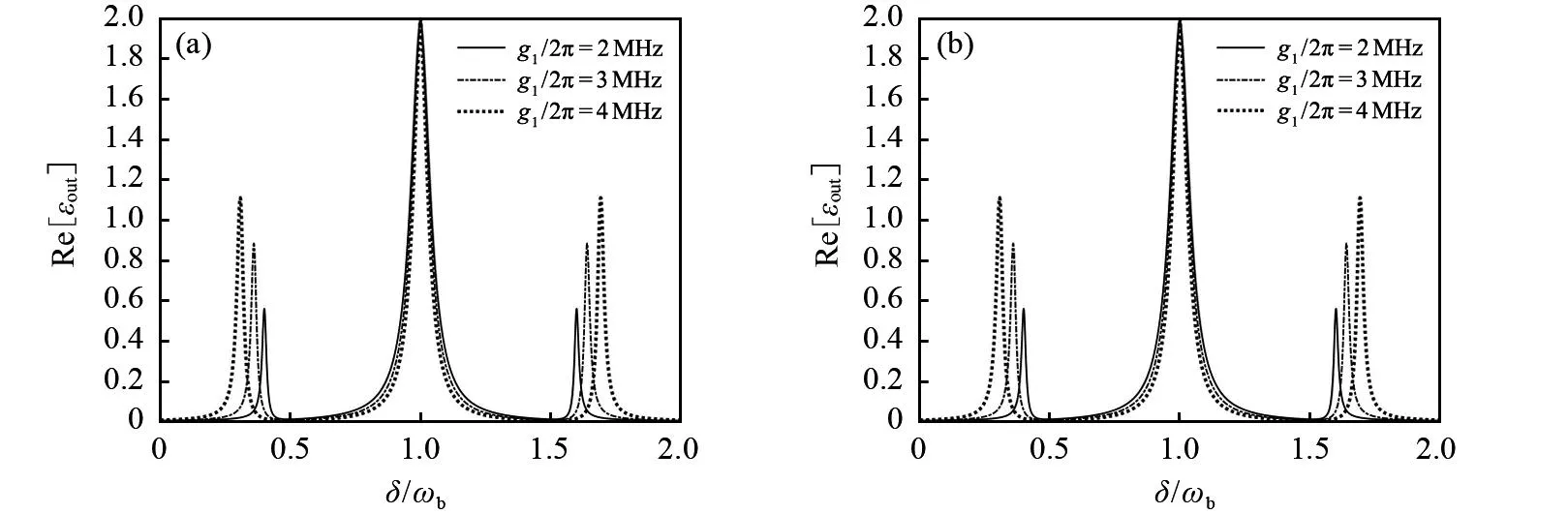
图4 不同腔1磁子耦合强度(g1)时吸收谱(Re[εout])与归一化探测场失谐(δ/ωb)的关系

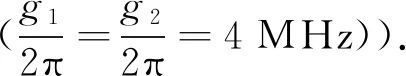
图5 不同磁子声子耦合强度(G)时吸收谱(Re[εout])与归一化探测场失谐(δ/ωb)的关系

3 输出场的法诺共振

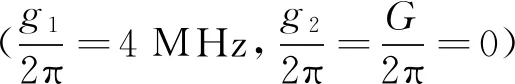
图6 不同耦合参数时非对称吸收谱(Re[εout])中的法诺共振谱线随归一化探测场失谐(δ/ωb)的变化关系

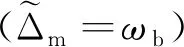
4 混合双腔磁力系统中的快慢光传输

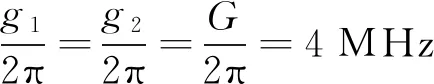
图8 不同耦合参数时群延迟(τg)与归一化探测场失谐(δ/ωb)的变化关系

5 结论

在混合双腔磁力系统中对探测场的吸收谱进行研究表明:由于非线性磁子与光子的相互作用和声子与磁子的相互作用,在吸收谱上出现了磁子诱导透明窗口(MIT)和磁力诱导透明窗口(MMIT);通过选择合适的系统耗散和耦合参数对系统进行调制,不但可以增强其透明效果,而且还可以实现快慢光的便捷调控以及提高快慢光的传播速度;通过调节系统中的耦合参数和非共振相互作用,在输出光谱中可获得法诺共振现象．本文研究结果可为量子比特操控、光学传感器和光纤通信系统制造以及量子信息存储的研究提供参考．在今后的研究中,我们将对其他模型中的诱导透明现象、法诺共振现象等进行研究．