基于BB-递归核函数SVR算法的U型折弯件模型参数优化研究

徐承亮,胡梓枫,曹志勇,张详林

(1.广州科技贸易职业学院,广东 广州 511442;2.湖北大学材料科学与工程学院,湖北 武汉 430062;3.华中科技大学材料成形与模具技术国家重点实验室,湖北 武汉 430074)

0 引言

U型折弯件回弹受到多种因素影响,例如工件尺寸、力学性能和负载条件等,由于这些因素的存在,使得控制弯曲回弹变得更加困难[1]。弯曲回弹是一种高度复杂的非线性控制问题。在实际工程应用中,通常采用多种方法来解决,其中经常使用的有反复试错法、有限元法和经验公式法[2]。这些方法都有其适用的场景和优缺点,可以根据具体情况来选择使用。尽管反复试错法和有限元法在解决弯曲回弹问题中具有一定的优势,但是它们的实施过程非常耗时,需要大量的计算资源和时间。另一方面,经验公式法虽然计算速度较快,但是其误差较大,难以满足精度要求。

为了解决这些问题,可以考虑使用支持向量回归(SVR)、变量保真等机器学习算法来对弯曲回弹进行预测和控制。支持向量回归法利用线性函数把原始空间映射到高维数据空间[3],需要耗费大量CPU时间计算模型精度,计算复杂度较高,模型精度受不确定因素影响比较大。变量保真算法可以在保证精度的同时,大大降低计算时间成本,然而目前使用的变量保真算法一般是基于差分映射或梯度算法,只有在输入输出函数和目标值之间的差异较小时才能获得较高的模型精度。现实情况是输入输出函数和目标值之间的差异往往较大,这样得到的模型精度会比较低。因此,需要寻找其他方法来降低计算时间成本和提高模型精度。

分支界限法(branch and bound,BB)是一种精确度高的非线性降维-变量保真算法,通常调用支持向量回归(SVR)进行收敛性判断,通过全局分层搜索和筛选特征变量子集来实现。SVR作为一种基于回归问题的支持向量机,可以用于预测和控制弯曲回弹问题。然而,其在优化核函数参数时,通常需要采用交叉验证等耗时的方法来判断其收敛性[4]。为了解决这个问题,可以采用一些优化算法来加速核函数参数的优化,例如BB法[5]、遗传算法[6]、蚁群算法[7]等。这些算法可以在保证精度的同时,大大降低计算时间成本。BB法的收敛是基于单调性准则的,为了保证BB法依据某种单调性准则快速收敛,需在 SVR内构思并部署一种依据某种收敛规则、单调性的、递归形式的核函数,那么BB法在每一层搜索新的数据节点时,会依据 SVR内的这个单调性的递归核函数准则进行收敛判断,从而迅速实现对特征变量子集进行筛选和降维,大幅减少生成精确SVR训练数据集的样本数据的规模和计算时间,在保证模型的收敛精度下,提升高保真弯曲回弹元模型的生成效率[8]。这种方法在U型弯折件的研究中得到了广泛应用,在实验中,可以设计相应的设备和装置,以支持这种方法的实施和验证。

1 实验设备与装置

在实际工程中U型弯折件是一种应用非常广泛的部件,图1(a)所示的是研究使用的模具设备,图1(b)所示的是模具示意图,主要由上、下两个模头组成。

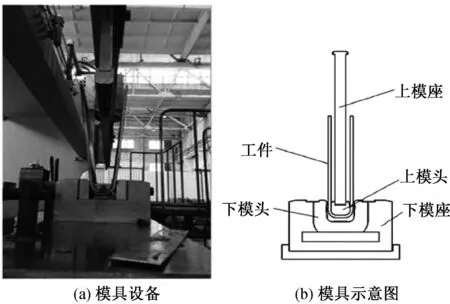
图1 研究使用的模具设备及示意图

如图2(a),t为板厚,c为上下模间隙距离,r为上模圆角半径。如图2(b),d为上模宽度,板料回弹后折弯件的端面开口角度设为α,板料回弹后折弯件的圆角半径设为R,由于回弹,弯曲件的端面张开角α发生了变化。在U型弯件的研究中,上模的宽度d、板料回弹后的端面张开角α以及圆角半径R等都是弯曲回弹非常重要的参数。而弯曲回弹和上模宽度、材料性能、上模压下量、上模下压速度以及板料厚度等因素存在高度复杂非线性关系,因此很难通过内置规律的解析模型来确定它们之间的关系。为了解决这个问题,可以采用一些先进的计算方法和技术,例如机器学习、数值模拟等,来对这些参数进行建模和预测。通过这些方法,可以更好地掌握这些参数之间的关系,为实际工程的应用提供支持。

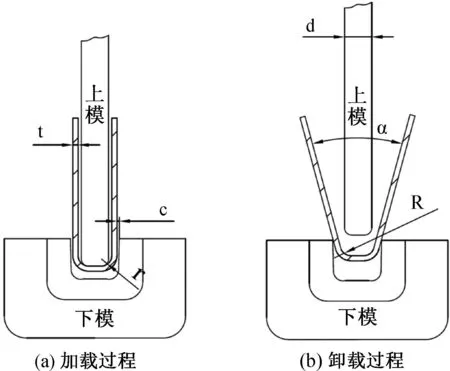
图2 U型板材弯曲模型

图3所示部位及回弹参数说明如下[9-10]:坯料长度为L,单位mm,坯料宽度为B,单位mm,板料折弯后高度为h,单位mm,上模宽度为d,单位mm,板厚为t,单位mm。为了获取弯曲成形后零件的三维点云数据,可以使用三维扫描测量仪进行扫描。扫描完成后,将获得的点云数据导入计算机辅助设计软件中进行建模。接着,利用有限元分析软件对生成的模型进行分析,可以获取成形零件的张开角α。通过改变输入参数,可以重复上述过程来获得训练和测试用数据样本集。这种方法可以帮助我们更好地理解弯曲成形后零件的特性和性能,为实际工程应用提供支持。

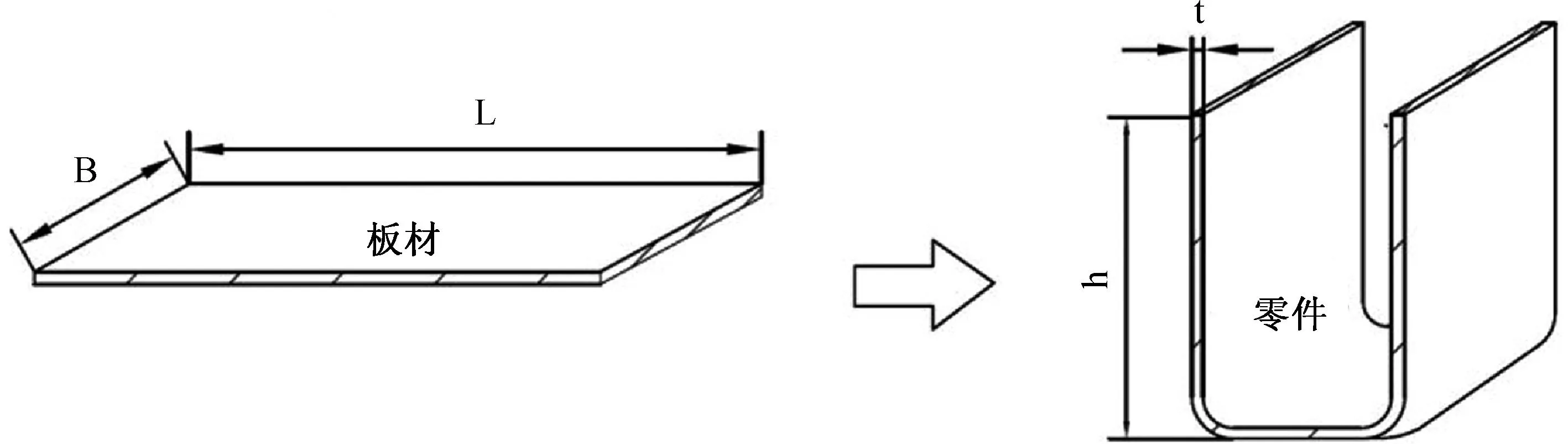
图3 U型折弯工件外形尺寸

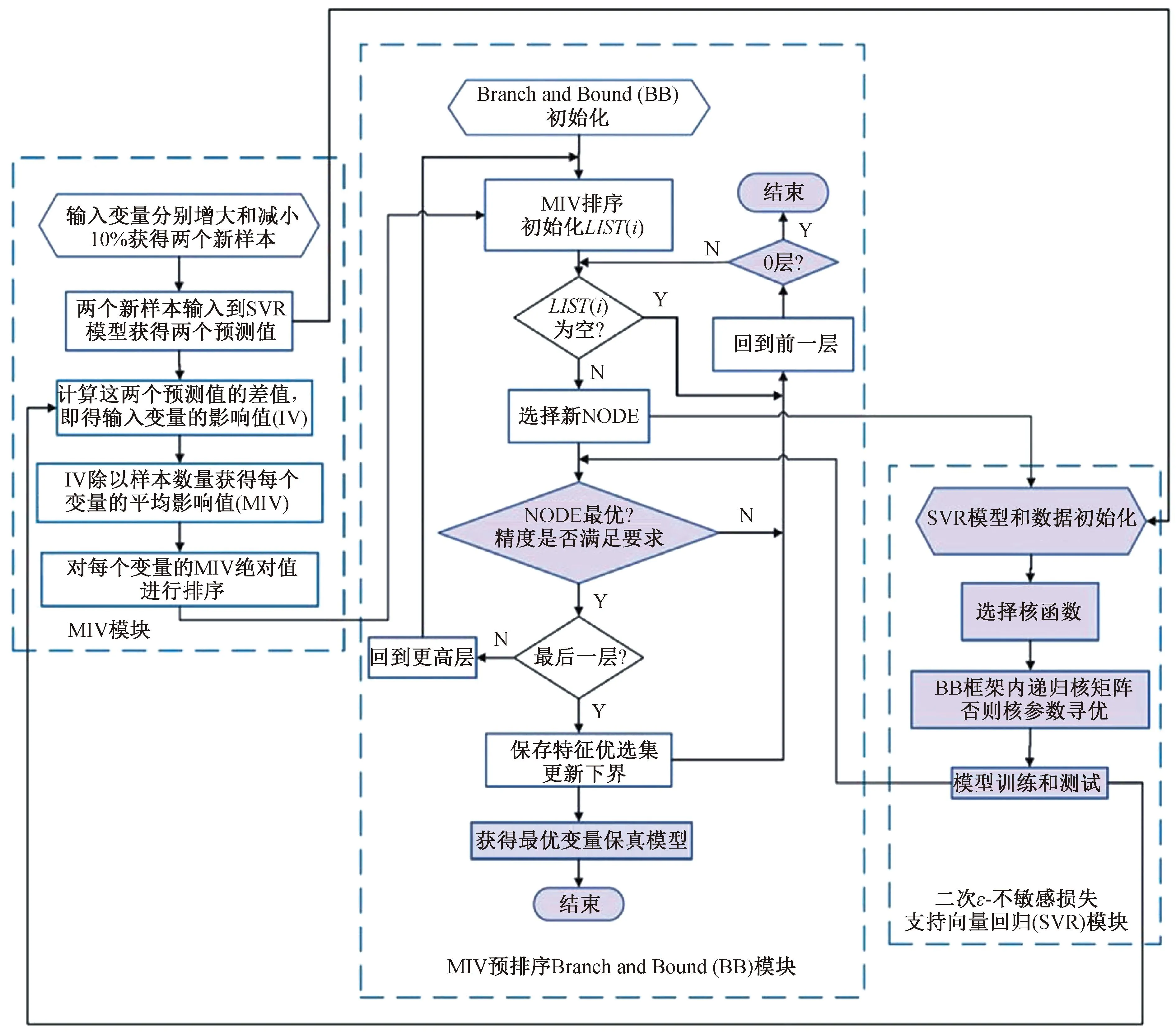
图4 MIV预排序BB的基于递归核函数矩阵SVR的高保真弯曲回弹模型

2 算法流程

平均影响值(MIV)反应了神经网络中权重矩阵的变化情况,被认为是在神经网络中评价变量相关性最好的指标之一。正交实验法进行多因素方差分析需要考虑各个变量之间复杂的耦合关系,不容易识别出重要的特征变量,将MIV平均影响值的思想应用于支持向量机回归中实现非线性的特征变量筛选,以提高特征变量的识别精度、减少训练和识别时间。基于MIV预排序的BB递归核函数SVR算法思路、技术框架与方案如图 4 所示,主要有以下几部分构成。

1)平均影响值模块(MIV)。计算各特征变量的平均影响值(MIV)后,再对分支界限法(BB)进行预排序,以提高特征变量的识别效率。

2)MIV 预排序的分支界限法(BB)模块[11]。为了避免SVR方法中耗时的交叉验证和寻优过程,采用基于递归核函数矩阵的方法,以缩短训练时间和提高计算效率。

3)二次ε-不敏感损失支持向量回归(SVR)模块[12]。我们将ε-不敏感损失函数定义为二次的,对SVR进行核参数寻优,最后对模型进行训练和测试。

算法结束,可获得高保真的影响弯曲回弹模型的主参数变量及其取值,这些数据将提供给第3部分中进行有限元模型的重构和模拟,并可获得板料回弹后的张开角α的预测值,算法结果见“4结果与讨论”部分。

3 有限元分析

在折弯条件(载荷和行程等)不变的前提下,通过改变基于递归核函数矩阵SVR算法提取出的板料厚度(t),上模宽度(d),上模圆角半径(r),上模行进速度(v)变量来分析不同参数对折弯件端面张开角α的影响。根据实验现场情况和经验,t的取值范围为5～12 mm,d的取值范围为60～90 mm,r的取值范围为5～12 mm,v的取值范围为10～25 mm/s,为了分析U型折弯件的弯曲回弹量及其补偿机制,构建了由上模(冲头)、半活动模、下模座和薄板构成的有限元模型,如图5所示,上模使用载荷F(4.5 kN)冲压薄板板料,半活动模支撑在下模座内,在载荷F的作用下,冲头接触板料并将板料往下压,板料接触到半活动模凸起部位,在载荷的作用下,半活动模下部凸起部位接触到薄板底侧,此时的半活动模侧面凸起压住薄板侧面同步旋转,从而可以实现U型折弯件的回弹补偿。使用BB递归核函数SVR算法快速获取目标函数(张开角α/2)为最小时的主要工艺参数组合(t,d,r,v)的数据,根据该数据(t,d,r,v)进行有限元模拟,并预测张开角α/2数据,根据角度数据,采用反三角函数,就可以确定弯曲回弹补偿装置的结构尺寸。算法优化得到的t为12 mm,d为90 mm,r为9 mm,v为10 mm/s,这些数据用来重构分析弯曲张开角的有限元模型。有限元分析结果见“4结果与讨论”部分。

图5 U型折弯件弯曲及其回弹补偿有限元模型(采用半活动模)示意图

4 结果与讨论

基于MIV预排序的BB递归核函数SVR算法结果讨论如下,表1 给出了板料长度L等10个输入变量的MIV(平均影响值)排序结果,参数说明见表1.如表1所示,在10个输入变量中,板料厚度t,上模宽度d,上模圆角半径r,上模行进速度v分别位于MIV排序的前4位,对U型折弯件的成形过程和性能具有很大的权重影响。板料厚度t和上模宽度d直接影响折弯件的尺寸和形状,上模圆角半径r则影响折弯件的圆弧部分的半径和曲率,而上模行进速度v则影响折弯件的成形速度和应力分布。

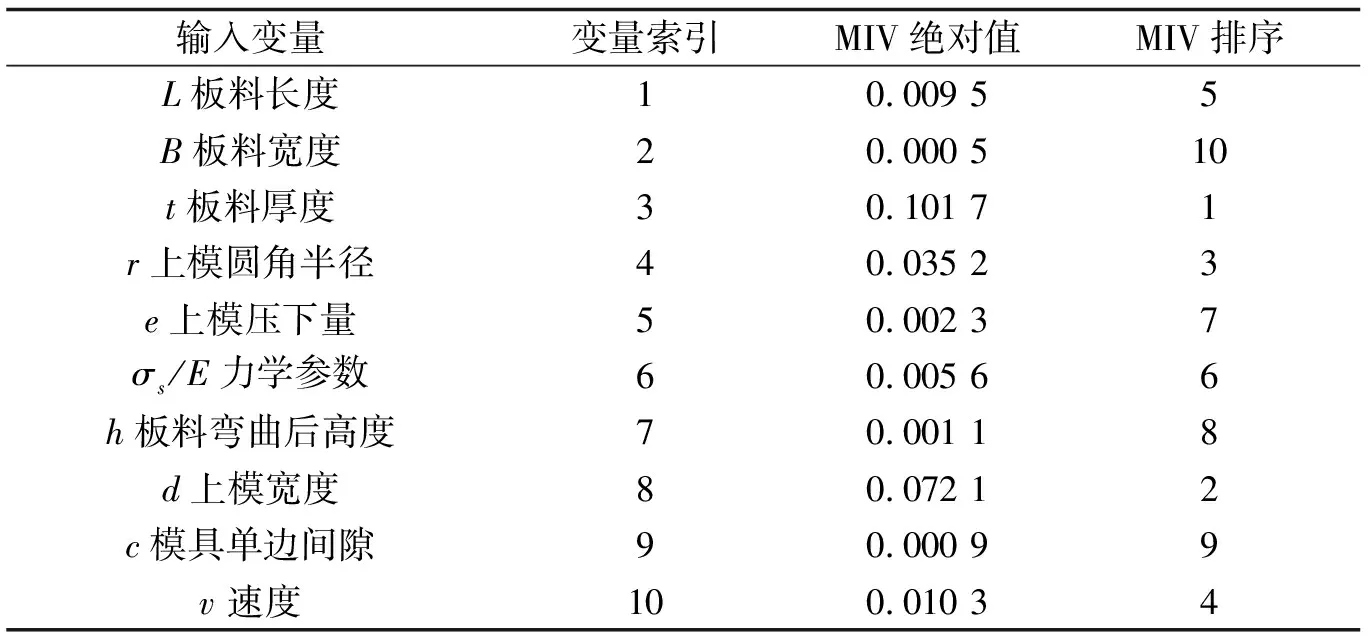
表1 输入变量的MIV排序结果

表2所示是一个最优变量集{t,d,r,v}的详细数据表,是由输入变量进行特征变量的降维分析而得到。观察表2,我们可以得到当特征变量子集为板料厚度t、上模宽度d、上模圆角半径r和上模行进速度v这4个变量时,维度为4,该模型的决定系数(R2)为0.982 147 ,决定系数最高,均方误差(MSE)为0.004 33,误差最小,模型预测精度相对较高。模型维度较高,决定系数越低,MSE相对误差越大。

表2 特征变量筛选示例(测试集)

为了进一步分析BB递归核函数SVR算法预测的弯曲张开角α和有限元计算的弯曲张开角α之间的关系,采用由上模(冲头)、半活动下模、下模座和薄板构成的有限元模型,如图5所示。有限元模拟弯曲以及弯曲后回弹补偿方法如图6所示,将递归核函数矩阵SVR算法求解获得的参数变量数据集(t,d,r,v)及其数据输入到有限元模型中进行重构和模拟,并求解获得弯曲张开角α。图6(a)显示的是当冲头达到弯曲张开角α/2时的工件等效塑性应变(PEEQ)的分布图,从图中可以看到,当弯曲回弹补偿角度为α/2时的应力分布均匀,在半活动模底部以及侧部凸起的板料受力部位没有出现应力集中现象;图6(b)显示了冲头返回后的PEEQ分布情况,从图中可以看出,当冲头离开半活动模并向上移动时板料按照弯曲回弹的补偿量(α/2)进行了回弹补偿。在参数(t,d,r,v)不变前提下,为了验证算法的有效性,将BB递归核函数SVR算法,有限元法预测和计算的弯曲张开角α和实验测量得到的α进行了对比,如表3所示,BB递归核函数SVR算法和有限元法预测和计算的α分别为16.3°和17.5°,实际测量α为18.2°,尽管有限元计算结果更接近于实际值,但是BB递归核函数SVR算法能为有限元模拟提供参数(t,d,r,v)的数据,便于快速进行有限元模拟并预测指定张开角α,实现快速设计弯曲回弹补偿装置的结构尺寸。另外BB递归核函数SVR算法的计算时间仅为32 s,远远低于有限元计算的时间(1 423 s),大大节约了时间成本,提高了计算效率,并且仍能保证一定的预测精度,满足了方案可行性要求。

表3 不同实验方案下的折弯件弯曲张开角α对比

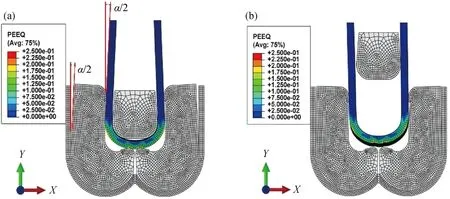
图6 (a)冲头达到单侧α/2的补偿量时的等效塑性应变(PEEQ)的分布,(b)冲头返回后PEEQ的分布

根据BB递归核函数SVR算法快速获取目标函数(张开角α/2)为最小时的工艺参数组合(t,d,r,v)的数据,根据该数据(t,d,r,v)进行有限元模拟,并预测张开角α/2数据,根据角度数据,采用反三角函数,就可以确定弯曲回弹补偿装置的结构尺寸。从而设计弯曲补偿装置使得下模具为半活动模具,以补偿弯曲回弹以生产更精确的零件。为了验证总体实验方案的可行性,根据t,d,r参数加工出具有回弹补偿装置的弯曲模具,如图7所示,从图7(a)中可以看出,根据BB递归核函数SVR算法和有限元预测的弯曲张开角α,设计弯曲补偿装置使得下模具为半活动模具,以补偿弯曲回弹以生产更精确的零件。图7(b)显示了弯曲回弹补偿后生产的U型零件。

图7 (a)采用弯曲补偿装置(半活动下模)的模具(b)用回弹装置和模具生产的U型零件

5 小结

高强度U型折弯件的弯曲回弹是一个十分复杂的问题,受工件尺寸、材料特性、力学性能等诸多因素影响,精确预测比较困难。此外,折弯件的弯曲回弹还受到生产工艺、设备精度等因素的影响,这些因素往往难以量化和控制。因此,在实际生产中,通常需要进行试制和调试,通过不断的实验和实践来寻求最佳的折弯工艺和参数,以减小弯曲回弹的影响。同时,可以采用一些先进的计算方法和技术,例如数值模拟、机器学习等,来对弯曲回弹进行建模和预测,以提高折弯件的成形精度和效率。本研究利用递归核函数矩阵部署到BB分支界限法中,以折弯件回弹角α为目标函数,高效地筛选出最优的特征变量子集{板料厚度t,上模宽度d,上模圆角半径r,上模行进速度v},其决定系数(R2)为0.982 147,均方误差(MSE)为0.004 33,模型预测精度相对较高。对算法模型的可行性进行了有限元模拟和实验验证,算法优化得到的折弯件参数为:厚度(t)为12 mm,上模宽度(d)为90 mm,上模圆角半径(r)为9 mm,载荷速度(v)为10 mm/s。BB递归核函数SVR算法、有限元模拟和实际测量的α分别为16.3°、17.5°和18.2°,尽管有限元结果更接近于实际值,但是BB递归核函数SVR算法可以为有限元模拟提供筛选出的参数(t,d,r,v)的数据,以快速进行模拟并预测张开角α,并实现回弹补偿装置的高效设计。