依惑而教:从物的等分到计数单位的等分
章颖

【摘 要】学生在学习“两位数除以一位数”的笔算时,通常会出现两个典型的困惑:除法竖式为什么要写“两层”?除法竖式为什么要从高位算起?基于困惑产生的原因,可以借助大小磁扣的“转换”帮助学生理解计数单位的两次等分。为此,教师将操作学具由小棒改为磁扣,设计“磁扣操作,体验计数单位的等分;体会记录,将除法竖式与两次等分过程进行关联”两个教学活动,在计数单位的转换中凸显两次等分记录的道理,加强学生对算法的理解。
【关键词】笔算除法;物的等分;计数单位的等分;学习困惑
一、学生在笔算除法中的两个困惑
除法竖式步骤多、书写繁杂,学生计算正确率往往不太高,是小学阶段笔算教学的重难点。其中,北师大版教材三年级下册“两位数除以一位数”内容是学生第一次接触多层记录的除法,理解起来有一定难度,因而学生通常会出现两个典型的困惑。
困惑一:除法竖式为什么要写“两层”?
教学68÷2的笔算时,教师通常先引导学生进行直观操作,再通过分物过程与竖式记录的对接,帮助学生理解算理。但事实上,教师教的过程与学生想的内容并不一致,学生存在困惑。
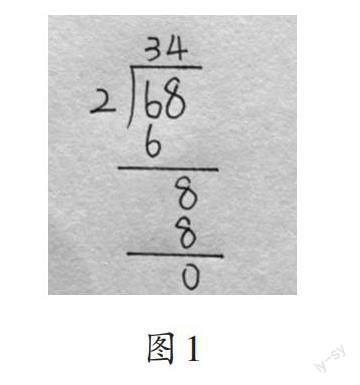
教师教的:把68根小棒平均分成2份,先分6捆,把6个“十”平均分成2份,每份30根,即60÷2=30(根);再把8根平均分成2份,每份4根,即8÷2=4(根);最后相加,即30+4=34(根)。两次分的过程用两层竖式进行记录(如图1)。
学生想的:“把68根小棒平均分成2份,6捆(6个‘十)和8根一起分,一次就能分好,写一层竖式更简单!”“二年级时学的除法竖式也只写一层。”“写两层太复杂了,直接写一层就能算出得数。”(如图2)
教师在课后访谈中发现,学生心里一直存有这样一个困惑:明明可以用一层竖式来记录,为什么还要写两层呢?可见,学生心里并不认同两层竖式的写法。这说明上述教学方式并没有体现两层竖式记录的必要性。
困惑二:除法竖式为什么要从高位算起?
教学68÷2的笔算时,教师一再强调:要先分6捆(6个“十”)小棒,再分8根小棒。试图让学生明白从十位算起的必要性。然而,在分小棒时,仍有学生直接把68根小棒一起分,不存在先高位再低位的过程;甚至还有学生先分8根小棒,再分6捆(6个“十”)小棒。这是因为68÷2这个例子比较简单、特殊,对帮助学生归纳“先分什么,再分什么”的过程的作用并不明显,所以才导致学生在应用竖式计算时不禁疑惑:加法、减法和乘法竖式都是从个位算起的,除法竖式为什么要从高位算起?
二、学生两个困惑产生的原因分析
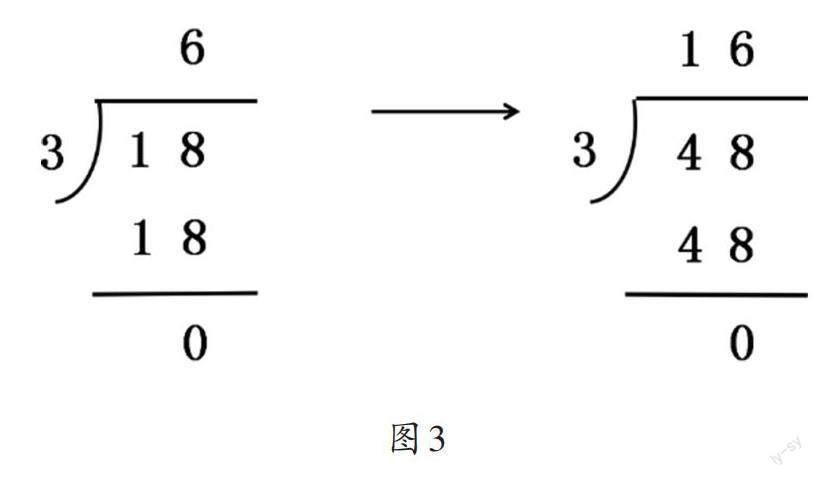
从学生角度看,既然二年级时笔算18÷3用“一层”竖式来表示,那么三年级时笔算48÷3也可以用“一层”竖式来表示(如图3)。而学生之所以会这么认为,主要有两方面原因。
原因一:学生的思维仍然停留在物的等分上
二年级时学习除法竖式18÷3是学生第一次接触除法竖式。教材中,不论是把18根小棒平均分成3份,还是把18个苹果平均分成3份,其实都是对物的一次等分,即把18个一平均分成3份,每份是6个一,相应地用一层竖式来记录。到了三年级学习除法竖式48÷3时,教材一般呈现4捆(40根)小棒和8根小棒,学生自然会把它看成一个整体,即48根小棒。把48根小棒平均分成3份,每份就是16根小棒,即16个一(由于数据比较小,学生能直接得出答案)。这一过程,学生是一次完成的,不需要转换计数单位,因此就用一层竖式来表示,导致学生很难体会“先分几个十,再分几个一”的除法竖式分层记录和“要从高位算起”的道理。
事实上,整数除法的核心在于“计数单位的等分”。在等分的过程中,先等分大的计数单位,有余时再与更小的计数单位合起来继续等分;在继续等分的过程中,先将大的计数单位转换成更小的计数单位,再与更小的计数单位合起来,使计数单位的数量增加,从而能继续等分下去。从二年级的“表内除法”到三年级的“两、三位数除以一位数的笔算除法”,等分过程变得更加复杂。两位数除以一位数对应以十、一为计数单位的两次等分,相应地用两层竖式来表示;三、四位数除以一位数乃至多位数除法,不能通过口算直接得到商,需要多次等分,通过多层竖式依次记录才能得到正确答案。可见,要让学生理解“除法竖式写两层”“要从高位算起”的道理,教师的教学就要由物的等分上升到计数单位的等分。
原因二:教学未能帮助学生从物的等分上升到计数单位的等分
为什么经过三年级的学习之后,很多学生仍然停留在物的等分,而对“除法竖式写两层”“要从高位算起”心存困惑呢?这可能与教师的教学设计有关。对于这一内容,教师通常会采用以下环节进行教学。
【环节一】经历平均分物的过程
教师呈现学习材料:把68个桃子平均分给2只猴子,每只猴子分到多少个桃子?
1.让学生先列出算式68÷2,再用小棒替代桃子进行分物活动:先分6捆小棒,再分8根小棒(如图4)。
2.抽象出口算过程:60÷2=30,8÷2=4,30+4=34。
【环节二】用除法竖式记录分物的过程
1.学生尝试用竖式记录分小棒的过程。
2.交流展示学生写的不同的竖式。
3.对比交流:将“先分6捆小棒,再分8根小棒”这两次均分小棒的过程与竖式的两层记录对接起来,再用分小棒的过程来解释竖式每一层记录所表示的意思。
4.學生规范书写除法竖式,并小结除法竖式的计算方法。
……
从上面的教学环节看,学生对算理的理解,与直观形象的“分”紧密结合。教师让学生先用小棒代替实物来操作,再将两次分小棒的过程与除法竖式的两层记录对应起来。在这一过程中,教师强化的是用除法竖式记录两次分物过程的表面现象,而没有分析其实质是计数单位的等分。试想,当学生将6捆小棒和8根小棒平均分成2份时,他们看到的是分物,还是分计数单位“十”和“一”?答案显而易见。学生用小棒进行操作活动,体验的自然是小棒的等分。当把成捆的小棒拆分开来,学生看见的直接就是“10个一”,并不需要“把1个十转换成10个一”,因此很难理解“先分几个十,再分几个一”的道理。
从以上分析中可以看出,学生产生这两个学习困惑的原因,是分小棒没有帮助学生从物的等分上升到计数单位的等分。
三、解决学生两个困惑的关键
如何解决学生的两个学习困惑,帮助学生从物的等分上升到计数单位的等分呢?关键是要凸显计数单位的转换。教学中,教师应借助适合的学具(磁扣)来体现计数单位的转换过程。
以笔算42÷3为例,教师可以用4个大磁扣和2个小磁扣来表示42(如图5),引导学生联想到计数单位“十”和“一”。把4个大磁扣和2个小磁扣平均分成3份,应先分4个大磁扣,平均分成3份,每份1个大磁扣,余下1个大磁扣;再根据“退一作十”,将余下的1个大磁扣转换成10个小磁扣。这种“把1个十换成10个一”的大小磁扣转换过程,促使学生用两层竖式表示等分过程,帮助学生完成等分中的升级,即先分十位上的几个十,将余下的1个十转换成10个一,和个位上的几个一合起来再分,从而让学生理解“除法竖式写两层”和“要从十位算起”的道理,同时也为后续学习三位数除以一位数和小数除法奠定基础。
具体而言,教师可以设计以下两个教学活动。
教学活动一:磁扣操作,体验计数单位的等分
这一学习内容教材安排了2个课时,先学习68÷2(首位能除盡),再学习48÷3(首位不能除尽)。教师设计教学活动时,将2个课时整合为1个课时,并将48÷3改为42÷3,作为例题进行教学。这样设计主要有两方面原因:一方面,首位不能除尽的除法更具有一般性,易于迁移到首位能除尽的除法;另一方面,42÷3比48÷3更方便学生操作学具。
1.任务驱动:42÷3的竖式怎么写?自己先试一试。
2.教学反馈:预设学生主要有两种不同的竖式写法(如图6)。
3.比较分析:如果这两种写法都对,你喜欢哪一种?
大部分学生喜欢竖式A,因为竖式A和他们之前学习表内除法时的写法一样。而竖式B要写两层,比较复杂。
4.教师提问:既然我们都认为竖式A比较好,为什么书上会选用竖式B呢?
这个提问是学生最困惑的问题。学生因为在二年级有学习除法竖式12÷3的经历,所以会从除法的意义进行思考。
5.回顾除法的意义:42÷3表示什么意思?表示把42平均分成3份,每份是几。
6.直观操作。
教师出示4个大磁扣和2个小磁扣(如图7),提问:这是42吗?你是怎么知道的?
学生思考:如何把4个大磁扣和2个小磁扣平均分成3份。
教师提问:先分什么?余下的1个十不够分怎么办?再分什么?
交流:刚才我们分了两次。第一次分4个十,将其平均分成3份,每份分到1个十,分掉3个十,还剩1个十。余下1个十不够分,转换成 10 个一。第二次分12个一,平均分成3份,每份分到4个一,分掉12个一,正好分完。
教师直接让学生尝试不同的算法,呈现学生的两种不同竖式,直面学生的疑问,而这疑问恰恰指向背后的算理,指向基于意义的操作明理。然后引导学生将教材中的操作学具小棒替换为大小磁扣,在平均分的过程中突出计数单位的转换。学生第1次先分4个十,剩下1个十不够分,发现必须把1个十换成10个一。由此,将两次平均分的过程呈现在学生面前。
教学活动二:体会记录,将除法竖式与两次等分过程进行关联
1.问题讨论:根据分的过程,你觉得这两种竖式写法,哪一种比较合理?很多学生认为竖式B比较合理。
2.教师追问:为什么竖式B比较合理呢?很多学生认为竖式B很好地记录了两次平均分的过程。
3.教师继续追问:你能在竖式B中找到两次平均分的过程吗?先分的4个十对应什么?要转换的1个大磁扣呢?在竖式A中能找到吗?
4.规范写法:用课件动态演示两次平均分的过程,学生用竖式记录。教师示范写法,并说一说计算过程。
5.比较:同样是两位数除以一位数,为什么12÷3 的竖式只需用一层来表示,而42÷3的竖式却要用两层?
6.结论:12÷3平均分了一次,所以是一层竖式。42÷3 平均分了两次,所以是两层竖式。
在充分体验计数单位的等分后,学生马上能将两次等分过程与两层竖式一一对应起来。这不仅体现了竖式分步记录的合理性,还将学具操作与口头表述、竖式书写之间进行多向沟通,从而使学生深刻理解除法竖式就是对两次等分过程的记录。学生在笔算除法中的“惑”自然就解了。
回顾整个教学过程,教师基于学生学习笔算除法的典型困惑,分析困惑产生的主要原因,依惑而教,将操作学具从小棒变为磁扣,在计数单位的转换中凸显两次等分记录,最终解决学生的困惑。
在小学阶段,学生一定还有不少类似的学习困惑。俞正强老师在《种子课2.0:如何教对数学课》一书中写道:为什么那么多学生对数学学习感到困惑,继而感到困难?这一定是有原因的。这个原因不是知识本身的对与否,而是教师“教”的这一行为的对与否。很多学生出现的学习困惑,与教师对教材和学情分析不到位,导致教学内容逻辑失序、学习素材选择失当、教学设计定位不准等有很大的关联。因此,教师应直面学生的学习困惑,认真解读教材,合理选择学习素材,精心设计教学预案,朝着正确的方向,上好每一节数学课。
(浙江省金华市教育教学研究中心)

