基于离散等收缩比的前体/进气道流向双乘波一体化设计

邬婉楠 肖雅彬 , 王立尧 岳连捷 杨 理

* (中国科学院力学研究所,高温气体动力学国家重点实验室,北京 100190)

† (重庆交通大学航空学院,重庆 400074)

引言

高超声速技术是指能使飞行器在大气层内高超声速机动飞行成为可能的技术,是多学科、多目标融合的新兴技术[1].以超燃冲压发动机为动力的高超声速飞行器可在大气层或跨大气层中以马赫5 以上的速度飞行,在空间运输、国家空天安全等领域拥有重要的政治和军事价值[2],是目前最具应用潜力的飞行器,也是各航空航天大国竞争的焦点[3].

高超声速飞行器的性能同时依赖于飞行器本身的气动布局和其所搭载的动力系统.从动力系统层面看,为了吸入高超声速来流、以及让排气尽可能完全膨胀,进排气部件不可避免地依赖更大的尺寸设计.这一特点决定了高超声速飞行器动力系统中的进排气无法像亚声速或超声速飞行器中的对应部件一样以较小的飞行器气动性能代价来完成设计.进排气系统较大的几何尺寸及其中更为复杂的内外流强耦合流动对飞行器的气动特性将带来重要影响.因此,高超声速飞行器必须将气动布局和压缩系统的气动外形综合设计,才能真正解决高超声速飞行中的内外流强耦合问题,真正意义上完成具备技术可实现性的飞行器设计方案[4-5].而进气系统位于飞行器最前端,直接对来流进行减速增压,因此前体/进气道一体化设计对超燃冲压发动机效能的发挥起着决定性作用.

20 世纪50 年代至今,前体/进气道一体化设计得到了长足的发展.研究经验表明,一体化的性能不仅依赖于前体和进气道单个部件性能,更受限于二者在几何和气动上的光滑过渡[6].一体化设计首先需要考虑的问题是布局方式.目前主要有两种一体化布局.(1) 独立进气布局,即进气道直接压缩来流.独立进气可进一步分为头部进气[7]、翼身融合[8]、双旁侧进气[9]以及背部进气[10].俄罗斯的“冷计划”、美国的HRE 计划以及Hyfly 计划中的进气道均采用了独立进气布局[7].这种布局的优点是可避免前体激波与进气道初始激波相互干扰诱导的复杂波系结构,性能较优.但是独立进气布局中进气道占有较大空间,压缩了飞行器的有效容积率,降低了飞行器的升阻比.(2) 前体与进气道流向串联,即来流先经过前体预压缩再进入进气道.以串联布局为代表的飞行器有: 搭载超燃冲压发动机的HAWC 高超声速巡航导弹[11]、搭载涡轮基组合循环发动机的SR-72 高超声速飞机[12],以及俄罗斯于2021 年发射的“锆石”高超声速导弹[13].该布局可提升飞行器的升阻比,压缩效率高;但是前体压缩后的非均匀来流、从前体发展起来的边界层以及前体激波与进气道初始激波的相互干扰通常会恶化一体化构型的性能[14].二者串联融合的方式林林总总,或依据激波形状定制捕获型线[15],或前体基准流场与内转式基准流场相惯[16].然而,由于缺乏可靠的一体化气动融合手段,研究人员更关注前体和进气道的几何融合,进气道的设计往往基于均匀来流.乔文友[17]基于非均匀来流提出了一体化的设计方法,从无黏的角度解决了进气道基准流场与前体基准流场的气动融合问题.但是由于激波的存在性尚未被解决,前体激波的给定很难从性能的角度出发,因此该方法具有一定的局限性.前体与进气道共用基准流场的方法尽管也是解决前体激波对进气道性能干扰问题的途径[18],但这限制了前体和进气道设计自由度与其效能的发挥.从设计方法的角度,目前前体和进气道主要采用无黏设计,无法计入黏性对性能的影响.优化手段可以弱化非均匀来流的影响,但是本质上没有解决前体与进气道气动融合的问题.

无论何种布局,一体化设计必须面对的挑战还有变截面问题.从不同部件的角度出发,流道截面的理想形状往往不同.从一体化的角度,模块化发动机的进气道理想入口截面应为近似矩形以便于多模块发动机并排安装;而从燃烧室的角度,圆形截面燃烧室对热、压力负荷的抵抗能力要优于矩形燃烧室[19],且圆形流道不存在角区流动,具有更好的流场品质.要同时满足不同部件对流道几何型面的要求,需要发展高超声速变截面流道设计方法.近年,变截面进气道设计得到了广泛研究,主要分为以下3 类.(1) 基于流线追踪的曲面加权融合法[20].即在同一个基准流场中分别根据入口形状和出口形状使用流线追踪生成两个型面,然后利用数学方法将两型面加权生成变截面进气道.此方法的代表是Smart 等[19]提出的REST 变截面进气道设计方法,将两族流线通过数学加权融合并不是按照气体动力学规律进行的,因此所得到的流场不能保持基准流场的特性.(2) 密切轴对称变截面流道设计方法.尤延铖等[21-22]采用Sobieczky 提出的密切轴对称理论发展了此方法,利用一系列共轴的、具有相同母线和不同中心体半径的轴对称基准流场实现变截面几何过渡,但是没有对反射激波进行处理,气流在反射激波及其后存在较强横向流动,因此隔离段内存在多道激波反射,流动均匀性有待提高.(3) 直接优化法.马里兰大学的Sabean 等[23]基于CFD 的直接优化方法完成矩形转圆形变截面进气道设计,优化目标是使出口压力均匀.优化设计方法的计算量对优化空间维数十分敏感,当几何型面需要被精确刻画时,优化空间的维数大量增加,计算量显著增大.且该方法以出口压力均匀度为优化目标,压力的均匀度并不能代表其他流动参数的均匀度.

面向总体约束,一体化设计不可避免地需要将进气道置于前体压缩后的非均匀流中,如何从气动的角度融合二者的基准流场,实现符合气动规律的流道变截面设计,保证出口流动参数均匀,对提升动力系统的推力性能与飞行器气动性能至关重要.为此,本文首先从理论上给出了进气道出口参数均匀的条件,然后基于该条件提出了新的前体/进气道一体化设计方法,采用数值模拟的手段初步研究了一体化构型的性能,与现有研究的区别在于: (1) 从理论上满足流场均匀的前提;(2) 进气道截面变化符合气动规律;(3) 前体/进气道基准流场气动融合,进气道完全基于非均匀来流设计.

1 基于离散等收缩比的前体/进气道一体化设计

为了使流道变截面符合气动规律,实现流场出口参数均匀,研究团队提出了均匀来流条件下的离散等收缩比的变截面进气道设计方法.现欲将离散等收缩比的思想推广到腹部进气布局的一体化设计中,从气动角度实现基于非均匀来流的变截面进气道设计,进而实现腹部进气布局中的前体/进气道一体化气动融合设计.为此,简要介绍基于离散等收缩比的流道设计方法,具体请参阅文献[24].

1.1 局部收缩比处处一致的理论依据

进气道的压缩过程是一个热力学过程,在此过程中,两个独立的热力学量唯一确定其他所有热力学量,速度等气动参量可基于能量守恒关系获得.因此,进气道出口均匀等价于流场中某两个热力学量/气动参数均匀.压比π30(流管出口压力与入口压力之比)与总压恢复 σ30(流管出口总压与入口总压之比)是进气道设计中两个重要的性能参数,决定了进气道的压缩效率且对发动机的推力有重要影响.不失一般性,将π30与 σ30作为两个独立的热力学量.图1 所示是任意的流管,基于热力学定律和能量守恒,可以推导出该流管的收缩比Cr03,π30与σ30的关系

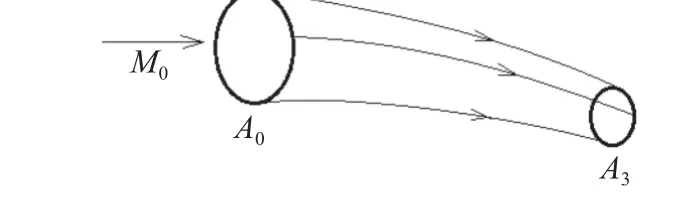
图1 流管示意图Fig.1 Schematic diagram of stream tube

图2 在π30-σ30平面上绘制了收缩比及出口马赫数等值线.其中,黑色曲线为收缩比等值线,红色曲线为出口马赫数等值线.任何一根收缩比等值线具有总压恢复极小值点,这些点连成一条直线,我们称之为熵极大线,这条线刚好是出口马赫数为1.0 的等值线.它将平面分成上下两部分,上部为超音速流动,下部为亚音速流动.对于一根收缩比固定的流管,其总压恢复、压比和出口马赫数等参量的变化仅有一个自由度,当其中任意一个参量给定时,其他参量被唯一确定.如果要求两根流管具有相同的入口和出口参数,那么二者的收缩比必须是相同的.因此,为了实现均匀的流场,需在设计上保证流场中所有流管的收缩比是相等的,这便是等收缩比设计方法的理论依据.

图2 流管收缩比及出口马赫数等值线Fig.2 Contraction ratio and outlet Mach number contours of stream tube

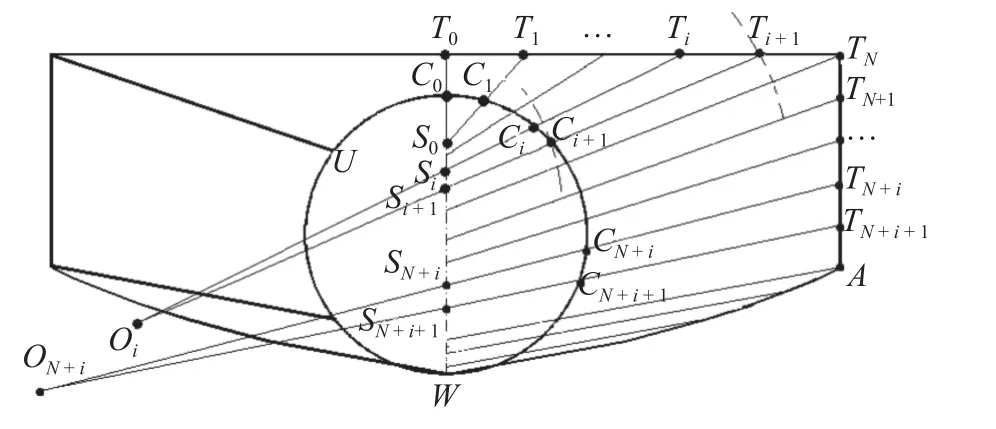
图3 矩形转圆形进气道 (垂直于来流方向)Fig.3 Rectangular to circular inlet (perpendicular to the direction of freestream)

1.2 基于流管划分的进气道设计

1.2.1 流管划分

为了阐述流管划分方法,以均匀来流为例,阐述如何基于该方法设计变截面内转式进气道.需要明确的是,该方法适用于任何给定进出口形状的变截面流道设计.

流管划分由进气道顶部对称面T0开始,将顶板捕获线划分为线段T0T1,T1T2,···,TN-1TN,侧板与顶板的交点为TN.对于T0T1,容易求得位于对称线上的S0,使该流管的入口S0T0T1与出口S0C1C0的面积之比等于进气道总收缩比Cr03.同理,根据Ti,Ti+1和Si的位置,容易求得位于对称线上的Si+1,满足收缩比Cr03.

侧板划分方法与顶板类似,只是侧板的长度需要根据设计目标定制.侧板捕获线被等分为TNTN+1,TN+iTN+i+1,···,随着i的增加,划分进行到圆形出口的下部,流管的出口面积开始急剧减小而入口面积SiSi+1Ti+1Ti变化缓慢,因此流管相邻边界的夹角越来越小,轴对称流动的半径|ON+iTN+i|趋于无穷大,接近二维流动,此后将不存在内收缩的流管.因此,侧板捕获线的长度有一个极限,当内收缩流管变为二维流管,便达到侧板的极限长度.

根据极限原理,可将图4 中的子流管近似理解为图5 中以Oi为对称轴、以TiCi为母线的轴对称流动.该流场由母线TiMNCi、半径为Rc=|OiSi|的中心体围成,轴对称入射激波TiP与中心体交于P,为了使总压恢复最大化,反射激波RS 应打在肩点Ci,即轴对称流场是消波的.对每一个轴对称流场中的型线进行优化设计,优化目标为该流场的总压恢复,在收缩比一致的情况下,通过调整每个轴对称流场的长度,保证流量加权平均总压以及其他流场参数一致.

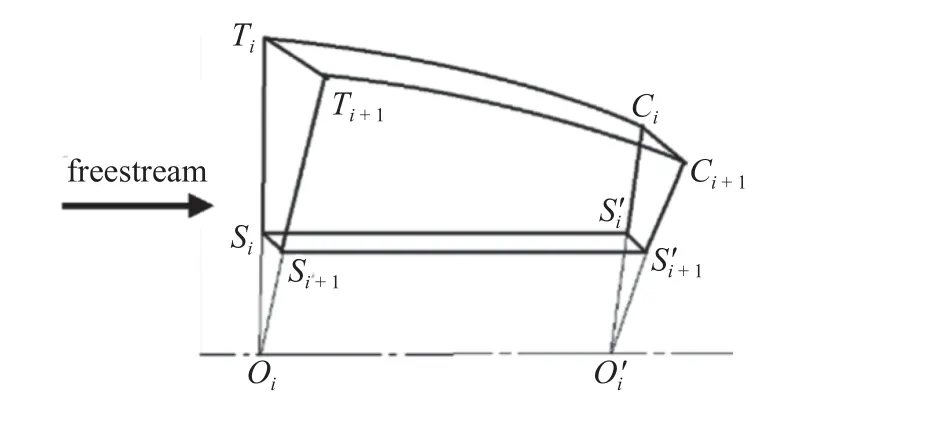
图4 流管立体结构Fig.4 3D structure of streamtube

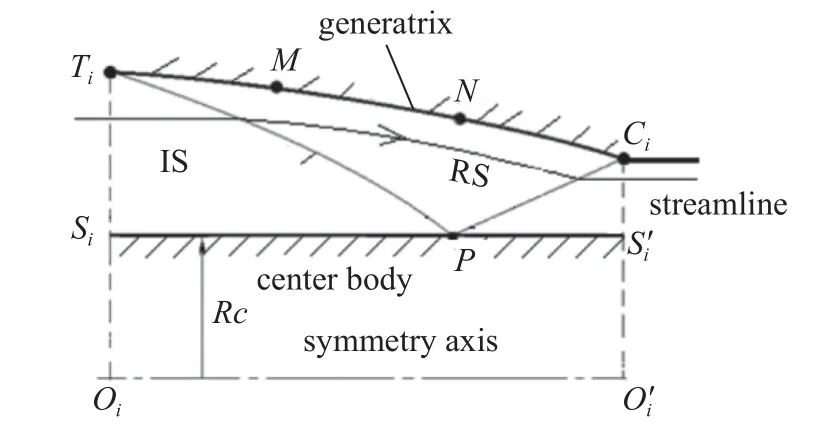
图5 虚拟的轴对称流场Fig.5 Virtual axisymmetric flowfield

1.2.2 流管匹配方法

为确保进气道流场中流管的存在性,流管之间应该完全没有横向流动,即相邻的轴对称流动中的一个必须是另一个的子集.由于每个轴对称基准流场的中心体半径与长度的比例不同且入射激波是向内弯曲的,不同中心体半径的轴对称流场并不相似,因此不能保证相邻两个轴对称流动中的一个是另一个的子集,所以流管间存在横向流动.然而,轴对称内收缩流场的入射激波仅在靠近中心圆柱的一小段区域才会显著弯曲,同时每个流场的长高比接近,所以入射激波后的大部分远离中心圆柱的区域横向压力梯度不显著,仅在靠近中心体反射点处有所增强.横向压力梯度最大的位置在初始激波的反射点处,即图5 中的P点.因此,在组合流管时使所有P点的x向位置相同,远离P点的区域流动的二维性增加,压力梯度会自动减弱.最终,这些流管的外缘就组成了进气道的型面.

1.3 前体/进气道一体化气动融合设计

一体化布局与飞行器的具体任务及其所搭载的动力系统相关,很难说某一种前体会具有压倒性的优势.乘波前体具有较高的升阻比,来流通过乘波体的预压缩会变为非均匀流,因此选取锥导乘波体作为前体来验证方法的可行性.前体/进气道一体化设计的难点在于二者压缩方式通常不同;就乘波前体/内转式进气道而言,经过前体压缩后,气流的方向转变为外锥流动,而内转式进气道需要将前体压缩后发散的流动转变为内收缩流动.外乘波前体与内转式进气道的一体化流场是一个三维流场,除对称面以外,流线不会在任何一个平面内,因此传统的基于均匀来流的流线追踪设计方法及其变体在解决二者气动融合问题时将遭遇困难.

本文将前体和进气道视为一个广义的进气道,首先选取前体压缩角为 4.4°,在Ma6.5 的来流条件下基于圆锥外流和流线追踪技术生成锥导乘波体,如图6 所示.

图6 锥导乘波体Fig.6 Cone-derived waverider

在已知前体流场的基础上,将文献[24]所述的基于均匀来流的二维(轴对称)设计方法拓展为三维设计方法,将待设计的流场拆分成一族背靠背的三维流管,然后逐一对每个三维流管进行设计.在图7中,A1A2A4A3-B1B2B4B3 是上述的一个三维流管在捕获面内的投影,A1A2B2B1 是外乘波体的被流管划分出的一部分,A2A3B3B2 是内转式进气道的主压缩面被流管划分出的一部分;A4E1F1B4 是唇口被流管划分出的一部分;A1A4B4B1 是捕获面被流管划分处的一部分,A3E1F1B3 是转平的进气道出口面积被流管划分出的一部分.在已知前体流场的基础上首先可以直接得出A1A2B1B2 的几何形状.使A1A4B4B1 的面积与A3E1F1B3 的面积之比等于进气道的总收缩比,由此,点A3,A4,B3,B4,E1 和F1 在捕获面内的坐标已知.接下来优化设计确定A3,A4,B3,B4,E1 和F1 的坐标.优化目标是总压恢复及唇口反射激波A4B4B3A3 在隔离段起始处(肩点)消波,由此获得此流管的三维外形.优化设计从对称面开始,依次向远离对称面的方向进行,每个优化设计所得流管都与即将优化设计的流管有一个共有流面,因此,每个待设计的流管只需设计一个新的未知流面.重复上述过程,待所有的流管设计完成后,将流管按照上述提到的方式匹配.即得到待设计的进气道外形.

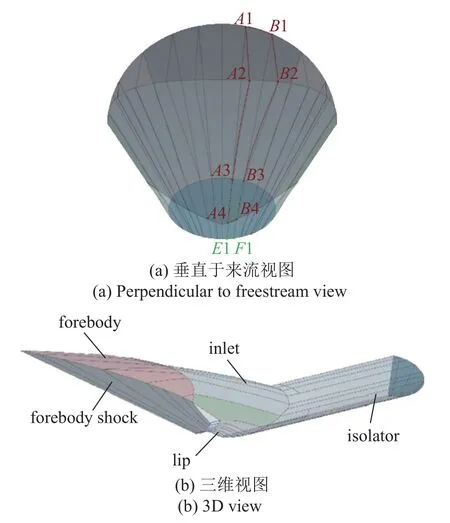
图7 三维流管的划分Fig.7 Division of 3D stream tube

获得的一体化构型如图8 所示.其中绿色的部分为外锥乘波前体,蓝色部分为进气道.进气道的捕获型线为非规则多边型曲线.由于完全基于非均匀来流设计,进气道的入口在对称面呈现类剪刀型.进气道出口为椭圆形,入口到出口的过渡完全符合气动规律.为了增强自起动能力,进气道内收缩段布置了抽吸腔,布置抽吸腔是工程上最常用的提升进气道起动及抗反压能力的手段.由于优化过程中直接考虑了黏性作用,因此无需对构型进行边界层修正.这也是该设计方法的一个优势.边界层修正的方法可在一定程度上规避黏性对性能的影响,然而,边界层的发展十分复杂,目前修正的手段多基于经验公式,该设计方法在优化的过程中,以“黑匣子”的方式计入了黏性的影响,因此不需要对构型进行额外的修正.

图8 一体化构型三视图Fig.8 Three views of forebody/inlet integrated configuration

2 性能研究

2.1 数值方法

采用有限体积法求解流场,对流采用二阶迎风格式,通量分裂采用AUSM 格式.气体物性参数采用分段多项式拟合,黏性系数采用Sutherland 公式,湍流模型选用k-wSST.使用ICEM CFD 生成四面体-三棱柱混合网格,边界层网格共28 层,首层厚度为0.01 mm,总厚度为30 mm.计算区域为对称模型的一半,如图9 所示,网格数量为270 万.入口条件为压力远场,出口条件为压力出口,前体、进气道及隔离段为无滑移绝热壁面.本文综合以往的经验,对前缘进行了3 mm 的钝化处理.进气道的攻角、反压特性及起动特性等都是工程上较为关注的性能,本文基于数值模拟方法初步考察Ma5,Ma6 和Ma7,攻角-2°～ 6°范围内一体化的性能.由于研究的目的是初步验证所提出一体化方法的有效性,因此暂不关注进气道的性能边界.此外需要说明的是,文中所给出的总压恢复、压比和马赫数等都是隔离段出口参数.隔离段是吸气式发动机的重要部件,它可以有效隔离燃烧室产生的反压,进而拓展进气道的工作裕度.从进气道出口到隔离段出口,即使进行消波设计,黏性损失也是不可避免的.因此,隔离段出口的性能参数才最具备参考意义.本文的主要目的是对设计方法的初步验证,一体化构型尺寸较小,网格数量相比于文献[25-26]较少,但是从文献[5]和文献[27-28]看,该数量级的网格可用于研究一体化构型的基本性能和捕捉波系结构.此外,本文所采用的数值模拟方法已经在超声速流动中得到了广泛应用[29-31],在此不做额外验证.

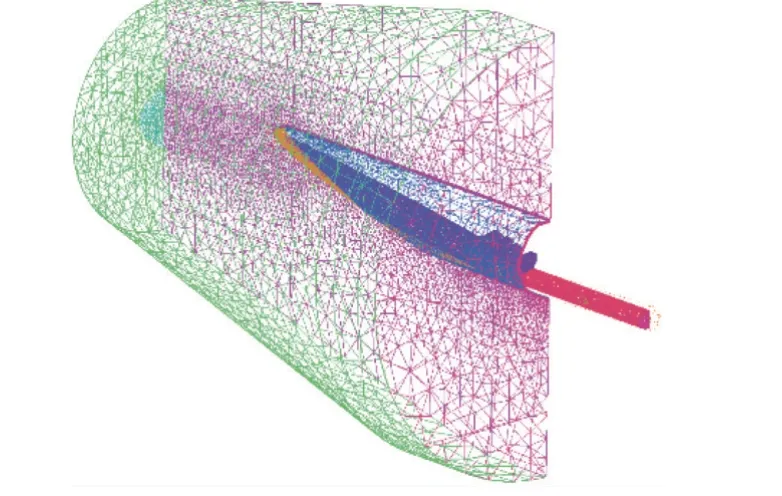
图9 计算域及计算网格Fig.9 Computational domains and computational grids

2.2 通流特性

图10 和图11 分别为来流Ma6.5 和攻角0°时一体化构型的流场结构.前体激波为轴对称外锥激波,进气道初始激波为非轴对称弯曲激波.在设计点,唇口会有少量的溢流,如果设计点激波封口,来流马赫数大于设计马赫数时,激波会打在唇口下游,诱发激波/边界层干扰,恶化进气道的气动性能.肩点的消波设计阻止了激波在隔离段内的反射,提高了压缩系统的总压恢复.隔离段出口的总压恢复为0.464,隔离段内未见激波的反射结构.由于进气道的设计完全以前体压缩后的流场为来流条件,前体激波与进气道的激波是完全匹配的,来流的非均匀性对进气道性能的影响已被考虑在内.抽吸腔泄除了约1%的低能流,设计点流量捕获率可达0.945,出口马赫数为3.13.前体激波和进气道初始激波相交于V 型唇口,一体化构型呈现出良好的多重乘波特性.隔离段出口未发展出较厚的边界层,核心流占比大,尽管没有给出边界层的物理模型,设计之初将边界层考虑在内而不是设计之后再修正,可以提升一体化构型的性能.对称面流场波系结构初步验证了本文所提出的一体化方法的有效性.

图10 对称面流场结构Fig.10 Symmetrical plane flowfield structure

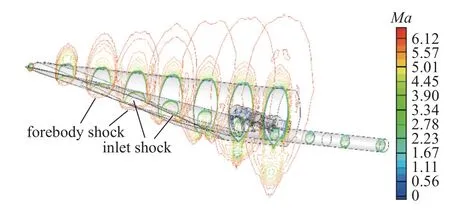
图11 轴侧图的马赫数云图Fig.11 Contour of Mach number in flowfield isometric view

为详细描述流场结构,现沿着流向截取11 个流动切片加以分析.如图12 所示,切片S1 和S2 位于前体,用以观察前体激波;切片S3,S4 和S5 位于进气道外压缩段,用以观察进气道初始激波和前体激波的复合乘波特性;切片S6 在V 型唇口尖端附近,用于观察进气道初始激波在唇口处的汇聚特性;S7 和S8 位于进气道的内收缩段,用以观察进气道反射激波特性;S9 和S10 用以观察隔离段内的流动特性,S11 用于观察隔离段出口特性.

图12 流向切片位置Fig.12 Location of slices along x-direction

图13 是上述11 个流向切片的流场结构.从切片S1,S2 和S3 可见,前体乘在圆锥激波上.S4 位于V型唇口前缘,与内收缩段的顶面、侧板和唇口相交,可见进气道初始激波为非轴对称的凹面,进气道激波与前体激波在唇口附近交汇.S5 进一步显示出进气道激波的一般形状,相比于上游的内转激波,该处激波内凹程度增大,并在唇口附近汇聚为一条竖直的激波反射线,从S6 可以看到这一趋势.进气道初始激波的形状进一步说明了发展基于非均匀来流一体化设计方法的必要性.非均匀来流影响下的进气道激波呈现复杂的三维特性,与均匀来流条件下的激波形状截然不同.初始激波经过反射后成为非轴对称的三维曲面,将向内收缩的三维流场一次转平并送入隔离段,这个三维反射激波被切片S7 显示.S8 和S9 展示隔离段内部的流动特性,可以看出核心流占比大.从S10 和S11 可见流向对涡结构,流向涡是内转式进气道特有的流动结构,其起源于喉道,由于存在横向流动,在横向压力的作用下,边界层向两侧偏转,在出口处形成对涡.在对涡附近,马赫数相对较低.图14 给出了隔离段出口的展向速度、纵向速度与轴向速度的比值.气流基本与隔离段平行,y方向受到流向涡的影响,偏转角的绝对值最大为5°左右.除了隔离段上侧气流角展向偏转较大外,大部分区域都基本接近0,而纵向偏转角十分均匀,基本接近0,这实现了反射激波将来流转平送入隔离段的设计初衷.

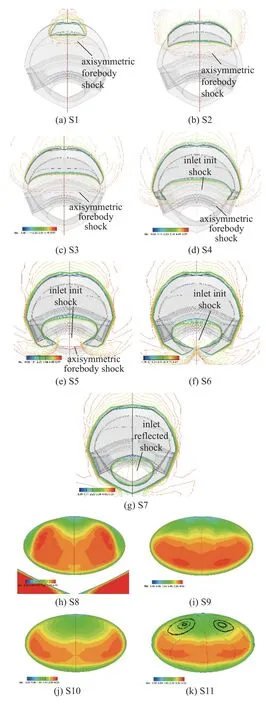
图13 设计点x 向切片流场结构Fig.13 Flowfield structure of slices along x-direction

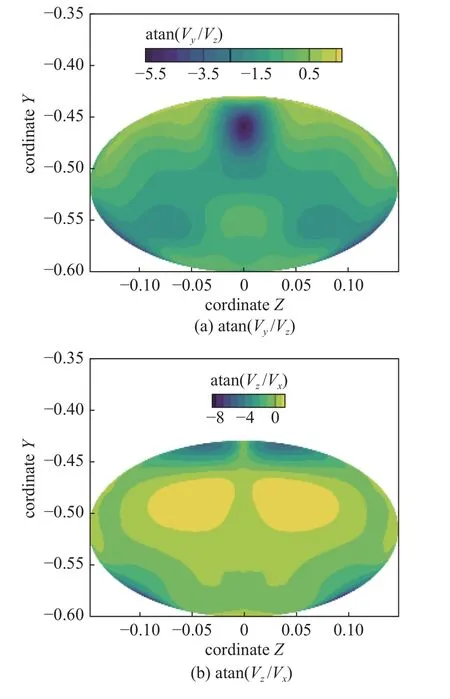
图14 隔离段出口气流速度角Fig.14 Air velocity angle at the isolator exit

2.3 攻角特性和侧滑特性

一体化构型的攻角特性是决定其工作裕度的关键因素.为了考察该设计方法的工作裕度,攻角及侧滑角特性的考察没有加入泄流槽.攻角特性与波系配置相关,在一体化设计中,如若忽略来流均匀性的影响,攻角状态下的性能更无法控制,因此,前体流场与进气道流场的匹配尤为重要.为此,初步考察了一体化构型在不同马赫数的攻角下的流场形态和性能.图15 和图16 分别为Ma5 和Ma7 条件下攻角范围内的流场结构.从来流Ma5 及不同攻角条件下的流场波系结构和流线形态可以看出,低马赫数条件下,激波被抬起,造成了唇口溢流,肩点在攻角为6°条件下有些许分离,但是分离规模很小,没有达到改变进气道波系结构的程度.进气道隔离段内在该攻角范围内均未见到明显的激波反射,且流动均匀.

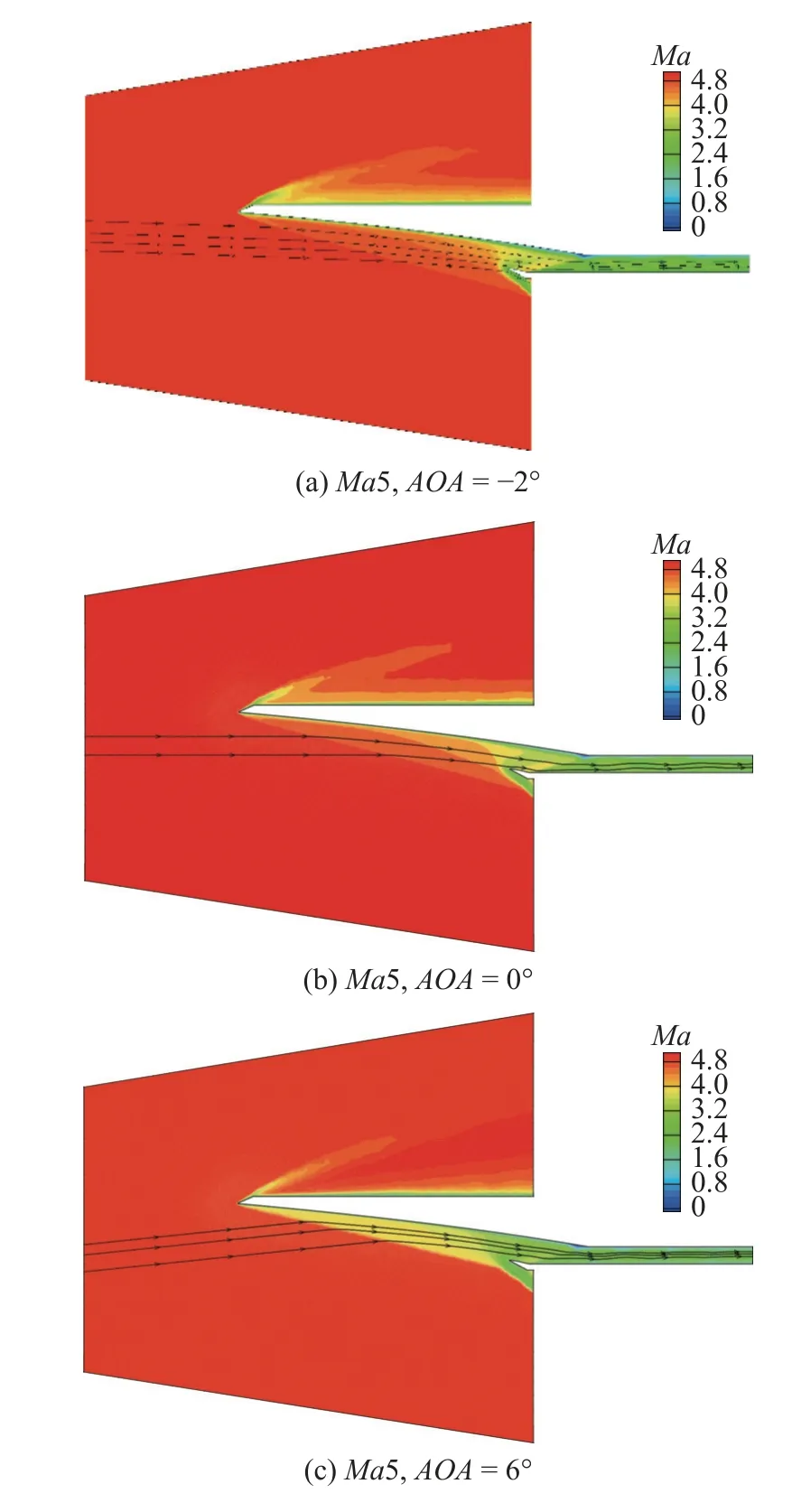
图15 Ma5 不同攻角下的马赫数云图Fig.15 Contour of Mach numner under different AOA at Ma5

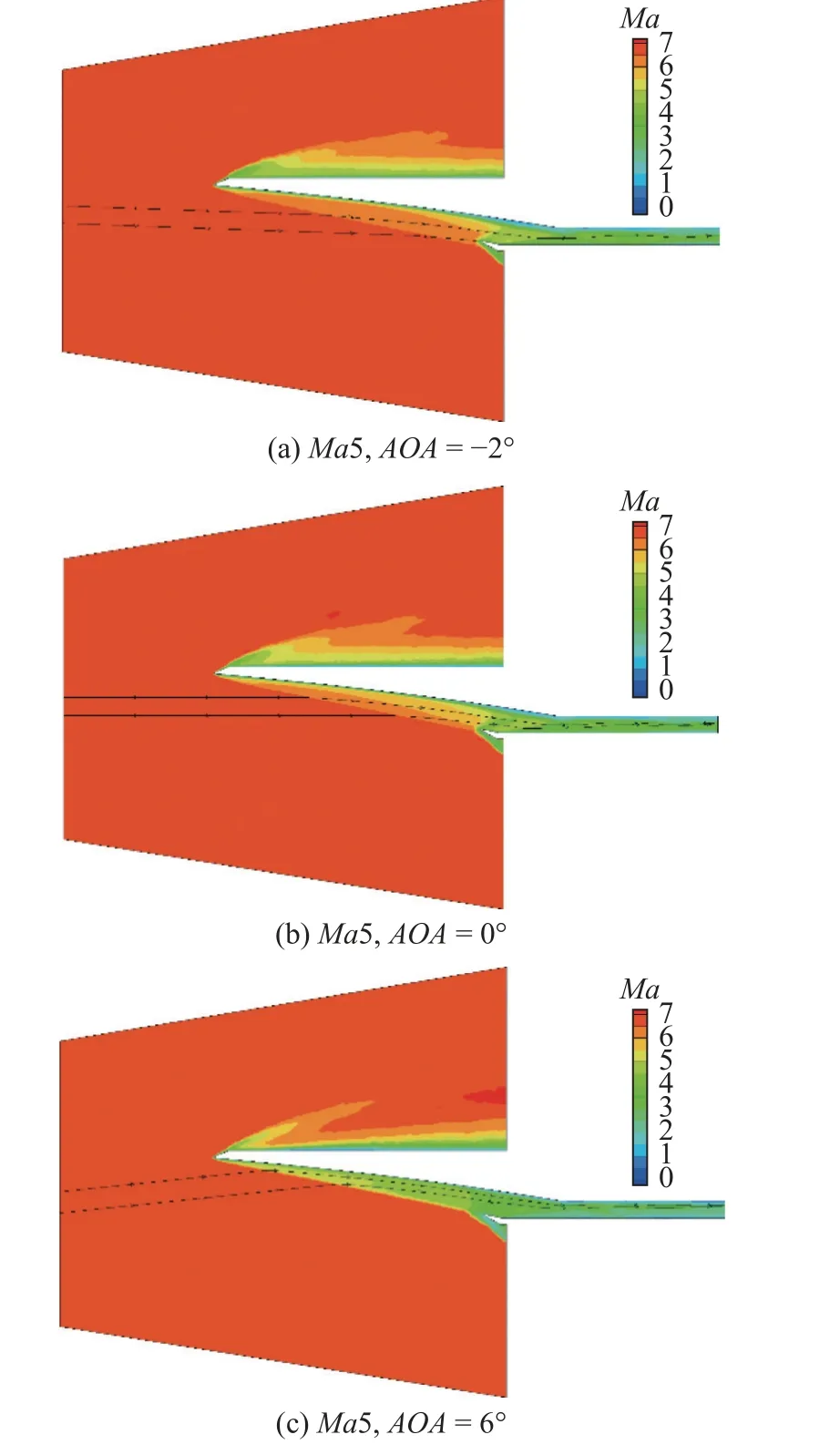
图16 Ma7 不同攻角下的马赫数云图Fig.16 Contour of Mach numner under different AOA at Ma7

在Ma7 条件下,激波进一步靠近唇口,肩点处溢流量减小,但是激波没有打到唇口下游,肩部小分离区消失,这说明了在设计点留有溢流窗的设计理念有利于提升进气道的工作裕度.由于激波强度增加,相同攻角下,压比相对于Ma5 状态下有所增加,总压恢复有所下降.该进气道的宽域性能良好,非设计点状态下,进气道仍能保持良好的波系结构,而且低马赫数条件下流量捕获特性依然能满足发动机的流量需求.

图17 给出了Ma5 时攻角状态下隔离段出口的速度偏转云图.在AOA=-2°时,y方向速度偏转与设计状态下相似.在流向涡的影响下,隔离段出口偏上的位置偏转较大,但相比于设计状态有所减小,出口偏下的位置偏转角比设计点有所增大,但是基本低于3°.而z向的偏转非常小,隔离段偏上的位置偏转稍大,其绝对值为6°左右,说明攻角下,进气道出口的气流特性依然未大幅度偏转设计状态.

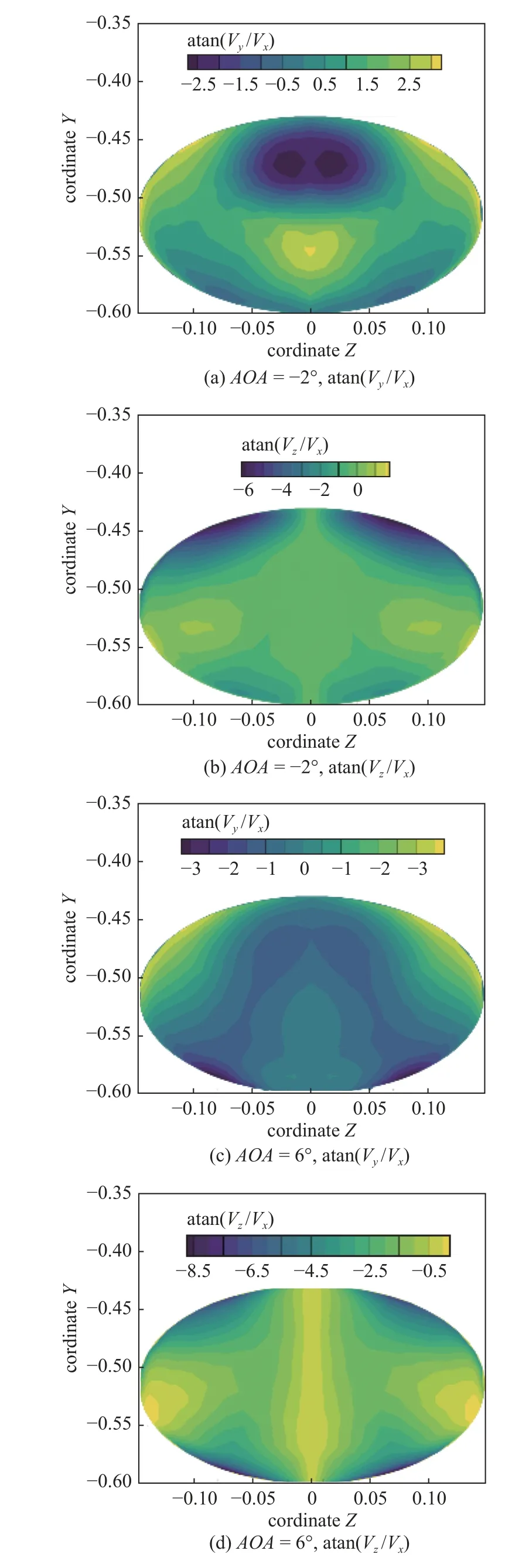
图17 Ma5 隔离段出口速度偏转角Fig.17 Deflection angle at isolator exit when Ma5

表1～ 表4 示出了Ma5～Ma7 下,攻角-2°～6°范围内,前体/进气道一体化构型的压比、总压恢复、出口马赫数及捕获率的数据.相同马赫数下,攻角越大,压比越高,出口马赫数越低,这是由于攻角越大,经过一体化构型的气流转折角越大,激波强度越强.总压恢复随攻角变化不是单调的,按照设计,0°攻角往往具有最大的总压恢复.同时,由于抽吸造成的流量损失,使得进气道的总压恢复由攻角和抽吸同时主导,变化较为复杂.流量系数在攻角变化范围内始终保持在较高的水平.该一体化进气道的攻角特性说明,本文所提出的一体化方法规避了来流不均匀对进气道性能的影响,所获得的构型具有较高的工作裕度.

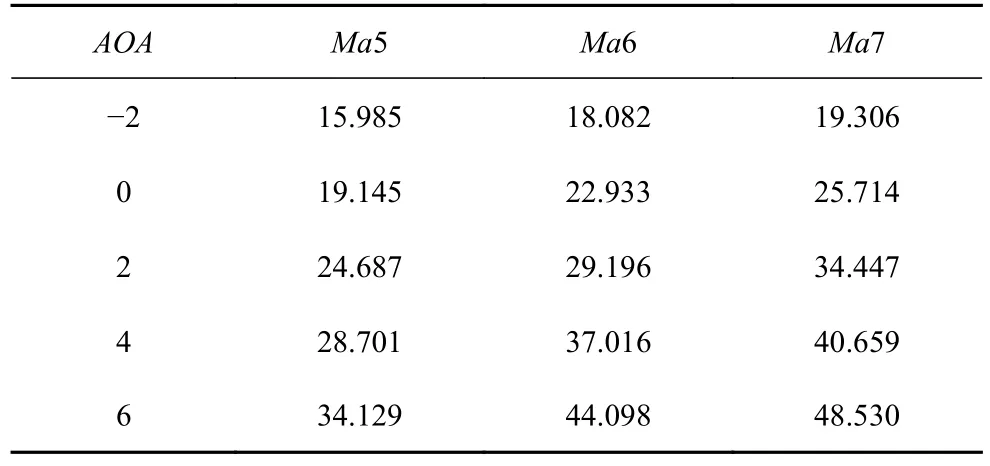
表1 Ma5～ Ma7 来流条件下,攻角-2°～ 6°一体化构型的压比Table 1 Pressure ratio of the forebody/inlet configuration when Ma5～ Ma7,AOA=-2°～ 6°

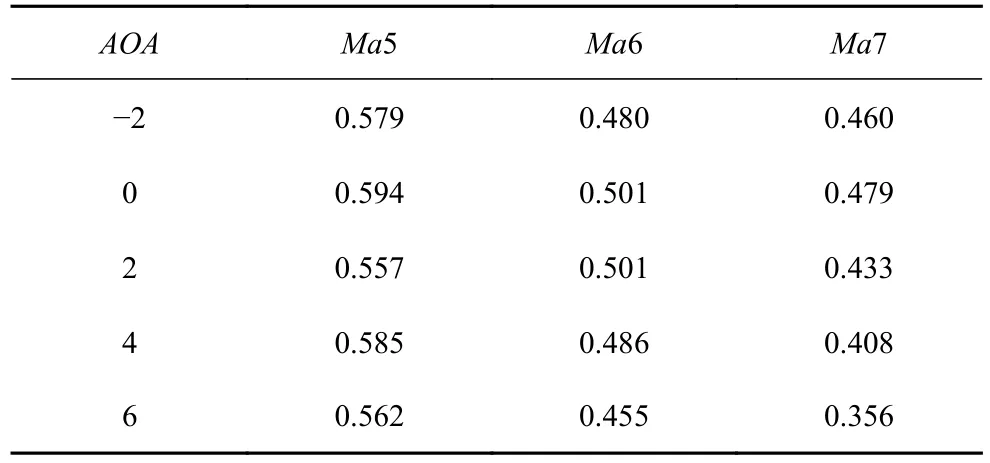
表2 Ma5～ Ma7 来流条件下,攻角-2°～ 6°一体化构型的总压恢复Table 2 Total pressure recovery of the forebody/inlet configuration when Ma5～ Ma7,AOA=-2°～ 6

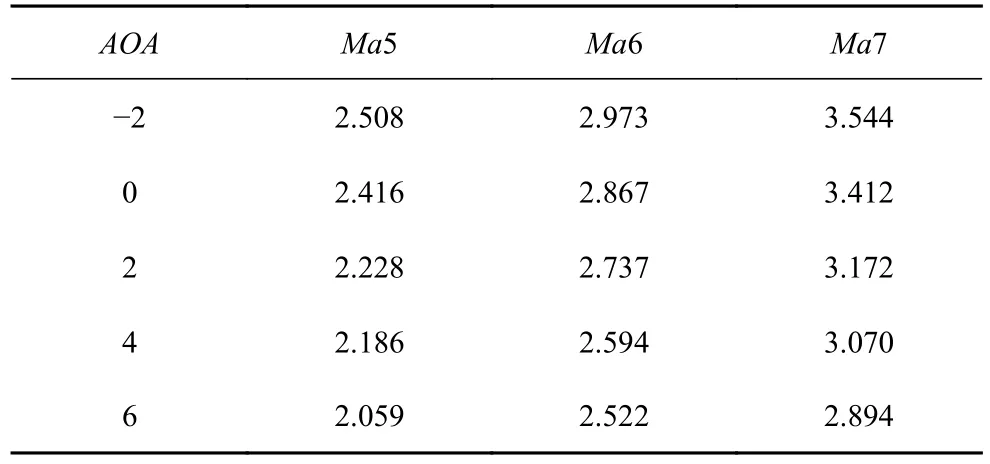
表3 Ma5～ Ma7 来流条件下,攻角-2°～ 6°一体化构型的出口马赫数Table 3 Mach number of the exit of the forebody/inlet configuration when Ma5～ Ma7,AOA=-2°～ 6°

表4 Ma5～ Ma7 来流条件下,攻角-2°～ 6°一体化构型的流量捕获Table 4 Flow mass capture of the forebody/inlet configuration when Ma5～ Ma7,AOA=-2°～ 6°

前体/进气道一体化侧滑角性能也是一体化设计过程中必须要考虑的问题,一体化构型的两侧过度下凹会导致在侧滑状态下的流量捕获率下降.为此,本文考察了一体化的侧滑性能,表5 列出了4°侧滑角状态下进气道的气动特性,可以看出,流量捕获率没有因为侧滑而大幅下降,可满足发动机工作的基本需求,同时出口马赫数和压比的表现说明,该状态下,进气道可达到理想的压缩量,总压恢复也可达到要求.

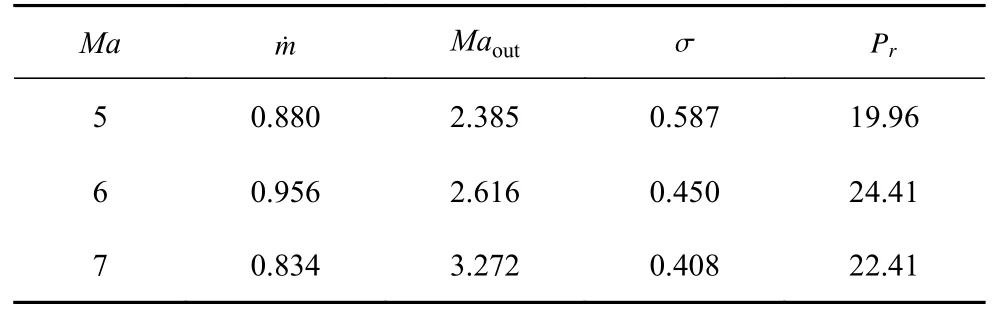
表5 侧滑状态下前体/进气道一体化性能Table 5 Integrated performance of the forebody/inlet under sideslip conditions

2.4 起动特性和反压特性

针对一体化构型的起动特性,采用数值模拟的手段,首先使来流马赫数下降到2.6 得到不起动流场,再以0.2 个马赫数为间隔逐渐增加来流马赫数,采用定常计算观察进气道内的低能流动是否消失.从图18(a)可以观察到,当来流马赫数为2.6 时,进气道被大尺度回流区封住,处于不起动状态,随着来流马赫数的增加,大尺度回流区的体积不断减小,在来流马赫数达到3.4 之前,回流区减小的程度并不明显.当来流马赫数超过3.4 后,回流区体积迅速减小.当来流马赫数达到4.0 时,回流区基本消除,进气道处于起动状态,来流马赫数达到4.2 时,低能流完全消除.因此得出结论,进气道可以在Ma4.0 实现自起动.

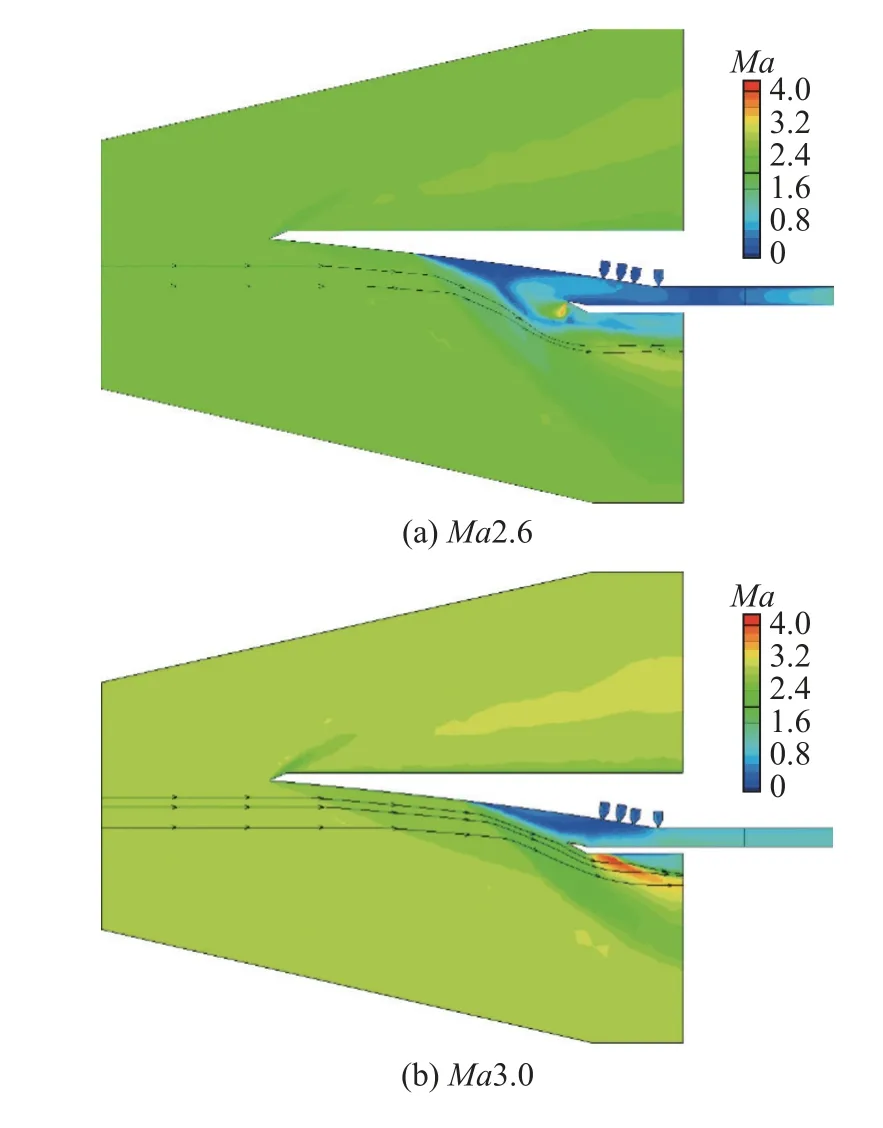
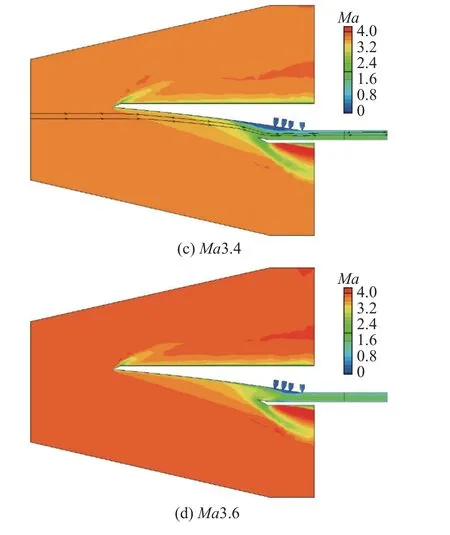
图18 前体/进气道一体化的自起动过程Fig.18 The self-starting process of the integrated configuration

针对前体/进气道的一体化构型,对其抗反压特性进行初步研究,尽管进行了一系列的数值模拟,由于仅是测试抗反压极限,图19 仅列出了200 倍反压条件下对称面的马赫数云图.可见,由于对涡的存在,使得隔离段上侧抵抗反压的能力不及下侧,反压推至第二道内通道抽吸槽,经过充分迭代后,结构保持稳定.因此得出结论,该进气道在此状态下可以承受200 倍反压.200 倍反压条件下,隔离段内可以观察到拟正激波串结构.然而该反压条件并没有破坏进气道唇口处的波系结构,仅仅是减少了隔离段的核心流占比.同时可以发现,适当的边界层抽吸不仅可以削弱肩部流动分离,增大核心流面积,还可以提高模型的抗反压能力.当然,前体/进气道一体化气动融合设计,合理的波系配置是提升进气道性能的先决条件.

图19 200 倍反压下前体/进气道一体化构型对称面流场结构Fig.19 Symmetrical flowfield in the integrated configuration of the forebody/inlet under 200 times backpressure

3 结论

基于等收缩比处处一致的思想,文章提出了前体/进气道一体化气动融合设计的新方法.实现了前体与进气道的气动融合、符合气动规律的变截面流道设计及流道出口参数均匀.并依托该方法设计了锥导乘波体/内转式进气道一体化构型,数值考察了一体化构型的性能.数值模拟初步研究了一体化构型的性能,设计点Ma6.5 的隔离段出口马赫数3.13,总压恢复0.464,捕获率为0.745,压比为24.3.进气道在来流Ma3.6 下实现自起动.计算表明进气道在-2°～ 6°,侧滑角4°范围内正常工作,并给出了压比、总压恢复、捕获率和出口马赫数随攻角的变化规律.