考虑压力敏感影响确定低渗透油藏有效注采井距

陈民锋，秦立峰，赵康，王艺文

（1.中国石油大学（北京）油气资源与探测国家重点实验室，北京 102249；2.中国石油大学（北京）石油工程学院，北京 102249；3.中国石油塔里木油田公司泽普采油气管理区，新疆 库尔勒 844800）

油田开发实践和相关理论研究表明，低、特低渗透油藏，普遍具有明显的启动压力梯度和压力敏感效应。由于启动压力梯度的影响，低渗透储层渗流规律不符合传统的达西定律[1-4]；而压力敏感即油藏开发过程中，储层压力降低，上覆岩层的压实作用导致储层孔隙喉道变小，渗透率降低，并且随着有效应力减小渗透率不能恢复至原始渗透率[5-9]。在油藏开发过程中，不可避免地出现储层压力变化，由于启动压力梯度和压力敏感的双重影响，使得油藏中流体的渗流特征和储量动用规律更为复杂。

考虑启动压力梯度对注采井距影响时，前人通过研究注采单元中驱替压力梯度与有效驱替范围的变化关系，建立注采单元内流体可驱动范围的计算方法，并由此来确定考虑启动压力梯度的水驱开发有效注采井距问题[10-11]。在考虑压力敏感效应和启动压力梯度对低渗透弹塑性油藏极限半径影响的研究表明，启动压力梯度增加了渗流阻力，降低了流体在介质中的流动能力，使得储量能够有效动用的范围明显缩小；而压力敏感的影响，主要体现在油井近井区域压力下降导致渗透率降低，使得储层启动压力梯度增大，进一步增加了储层流体的流动阻力[12-14]。

对于此类低渗透油藏合理注采井距的理论研究，一方面应考虑启动压力梯度、压力敏感在不同生产阶段的变化；另一方面应综合考虑注水井、采油井生产过程中在不同区域、地层压力不同变化带来的影响。而目前针对低渗、压敏储层有效开发的有关研究，大多没有全面考虑以上因素的综合影响[4-21]。

基于经典渗流理论，同时考虑启动压力梯度和压力敏感的影响，建立典型注采条件下渗流方程，使用“逐次稳定迭代法”计算方法，首先，定量确定出油、水井生产过程中，在储层压力变化区域内，由于压力敏感效应导致的渗透率变化，以及相应的启动压力梯度变化；然后，基于变化的渗透率和启动压力梯度，定量分析开发过程中地层压力的分布规律，进而计算不同因素对产量变化的影响，以确定满足要求的低渗透压敏油藏合理注采井距。

1 油藏压力变化过程及渗流方程

1.1 注采井间压力分布变化及其影响

对于低渗透压力敏感油藏，储层渗透率和相应启动压力梯度随地层压力的变化而发生变化，并使得地层压力分布呈现明显的不均衡性。

在图1 所示的示意图中，Ⅰ井为注水井，Ⅱ井为采油井；曲线1、2 分别表示井Ⅰ、井Ⅱ引起的地层压力随距离变化曲线，曲线3 表示2 口井压力变化叠加后的变化曲线。

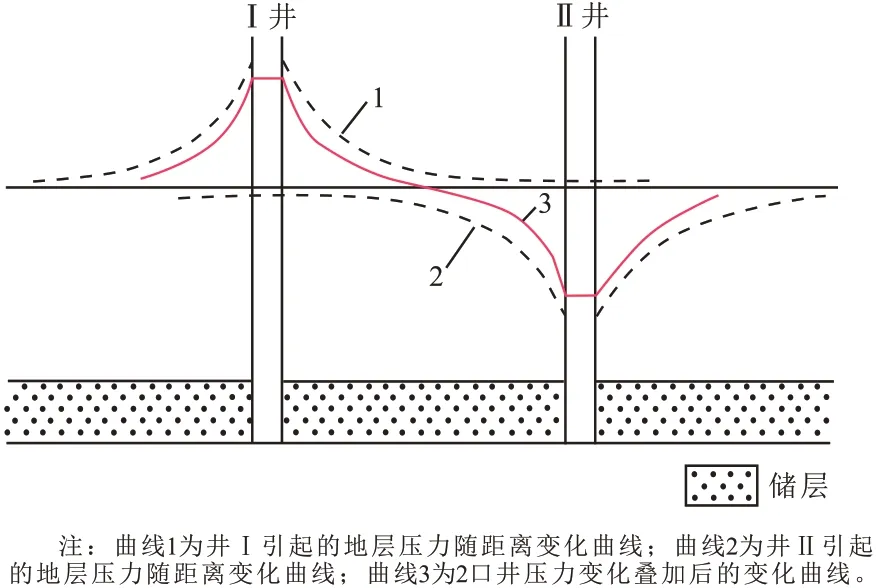
图1 注采井间地层压力分布示意图Fig.1 Pressure distribution between injection and production wells

根据图1 所示可进一步分析注采开发过程压力变化及其影响，采油井生产使得地层压力下降，而注水使得地层能量得到补充。对于注水井，在近井区域压力由原始地层压力逐步升高至注入压力，则在该区域范围内的渗透率由于介质变形（孔喉扩大）而提高，相应的储层启动压力梯度降低；对于采油井，在近井区域压力由原始地层压力逐步降低至井底流压，则在该区域范围内的渗透率由于介质变形（孔喉收缩）而降低，相应的储层启动压力梯度增大。该注采物理模型综合考虑了压敏效应（介质随压力变化而变形）在注水井端和生产井端的影响，因此，可以更精细地进行油藏开发设计。

1.2 基本渗流方程的建立

1.2.1 启动压力梯度与压力敏感表达式

室内岩心实验测试表明，低渗储层启动压力梯度满足以下变化关系：

式中：G为启动压力梯度，单位MPa/m；K为储层渗透率，单位µm2；μ为地层原油黏度，单位mPa·s；a、b为系数，其中a=0.032、b=0.601（取自XC 低渗油藏岩心测试实验统计结果）。

一般低渗透储层渗透率随压力变化遵循指数变化规律，由于升压、降压过程对储层的影响不同，因此，在升压、降压过程中介质压力敏感变形系数的取值不同。其表达式为：

式（2）—式（3）中：αu、αd分别为反映升压和降压阶段储层压力敏感影响的介质变形系数，单位MPa-1；K、Ko分别为储层目前、初始渗透率，单位µm2；p、pe分别为目前、原始地层压力，单位MPa。

1.2.2 基本渗流模型

对于图1所示的一注一采单元，设注采井中心坐标为（x=0，y=0），注水井位置坐标为（x=-d/2，y=0，其中，d为注采井距，单位m），采油井位置坐标为（x=d/2，y=0）。

考虑启动压力梯度和压力敏感效应的影响，基于单相不可压缩流体稳定渗流理论模型，建立典型低渗透油藏渗流方程，如下所示：

式中：r为距井距离，单位m；G为启动压力梯度，单位MPa/m；t为生产时间，单位d；re为供给半径，单位m；pwf为生产井井底压力，单位MPa；pe为地层压力，单位MPa；rw为井筒半径，单位m；Q为日产量（油水井），单位m3；μ为液相黏度，单位mPa·s；h为储层有效厚度，单位m。

1.3 渗流方程求解

1.3.1 基本求解思路

同时考虑启动压力梯度和压力敏感影响的渗流方程难以直接解析求解，采用“逐次迭代”计算方法来求解上述渗流问题。

1）对于给定条件、连续性（t）的非稳态生产过程，可以离散为多个时间段生产过程的组合（t＝Δt1＋Δt2＋...＋Δti＋...）。在每个时间段Δti内，渗流过程可以看作是相对稳定的，可以采用“压降叠加原理”处理注采生产导致的压力变化。

2）在每一个时间段Δti内，基本参数认为是不变的；而随压力变化的参数（渗透率等），取上一步计算结果，如第i段的计算参数值从第i-1步取得，直到计算至极限生产半径处。

对于每增加一个时间段Δti，传播距离就相应扩大Δri，则整个传播距离（半径）为r＝Δr1＋Δr2＋...＋Δri＋...。因此，计算步长可以具体由传播距离增幅Δri来实现，然后根据定生产压差（供给压力、井底压力给定）的方式进行计算。

由于井底附近压力等参数变化快，为了使计算结果更加精确，在近井区域的计算步长较小，后续适量增加计算步长。

1.3.2 压力分布计算表达式

以采油井为例，对于式（4），在地层中任一点Z，与采油井间的距离为r1（压力为p1），在rw～r1间压力分布表达式为：

式（5）左右两边对距离r取导数，可得驱动压力梯度为：

考虑启动压力梯度和应力敏感的影响，储层渗透率、启动压力梯度变化根据式（1）—式（3）确定，在Z处流体渗流速度表达式为：

由上式可得到产量计算公式为：

进而得到地层中压力分布表达式：

在生产过程中，储层渗透率、启动压力梯度都是压力、距井位置（距离）的函数。

则由于采油井生产导致的压力降为：

同理，在Z处（距离注水井为r2），可得到由于注水井生产导致的压力降为：

根据压降叠加原理，可得到一注一采条件下地层某点处压力表达式为：

式（5）—式（12）中：v为渗流速度，单位m/s；A为截面积，单位m2；pwi为注水井注入压力，单位MPa；d为注采井距，单位m；r1、r2分别为地层中某点距采油井、注水井的距离，单位m。

1.3.3 具体求解步骤

注采井间的压力分布计算具体步骤如下：

1）基于初始条件，如油层参数、给定产量（注采压差）、注采井距等，按照迭代计算步长（传播距离增幅Δri），根据式（12），计算当前传播半径ri下储层中压力的分布。其中，ri＝Δr1＋Δr2＋...＋Δri。初始第一步Δr1和后续距离增幅Δri可根据储层条件适当取值，一般可取10 m，如果储层渗流阻力小可以适当增大，这样可以在保证计算精度的条件下尽可能提高计算速度。

2）计算随压力变化的渗透率、随渗透率变化的启动压力梯度值；后续每个计算步长下储层参数取上一步计算结果，分别从采油井和注水井井底向外逐级迭代计算压力变化。

3）判断在当前传播半径下的驱替压力梯度dp/dr是否大于启动压力梯度G；如果满足，下一步增加传播距离（增幅Δri），继续迭代计算；如不满足，减少距离增幅Δri进行迭代计算，使得dp/dr＞G。在减少距离增幅Δri时，可以采取二分法的方式进行处理。即取增幅为Δri/2 进入下一步迭代计算，如果下一步满足计算条件，则继续往下计算；如果不满足，则增幅进一步二分，直至满足计算截止条件。

4）继续或截止计算条件判断。当生产井压力波传播到距离采油井rmo处，若此处驱替压力梯度等于启动压力梯度，则采油井极限动用半径为rmo；当注水井压力波传播到距离注水井rmw处，若此处驱替压力梯度等于启动压力梯度，则注水井极限动用半径为rmw。如果注采井距d＜rmo＋rmw，返回第一步进入下一步计算。如果不满足则跳入第五步。

5）当注采井距d＝rmo＋rmw时，完成求解压力场分布的完整步骤；然后输出满足条件下的计算结果——注采单元中压力场分布。

2 储层压力敏感性对开发的影响

在后续研究中，主要参数结合实际数据区间取值。其渗透率为（1～10）×10-3µm2，原始启动压力梯度为0.01～0.05 MPa/m，储层介质变形系数为0.01～0.10 MPa-1，原始地层压力为20 MPa，初定注采压差为10 MPa。

2.1 压力敏感对注采单元压力场的影响

基于以上建立的方法，在典型一注一采单元中，对比分析在相同条件下，有无压敏效应影响下的压力场分布，结果如图2所示。

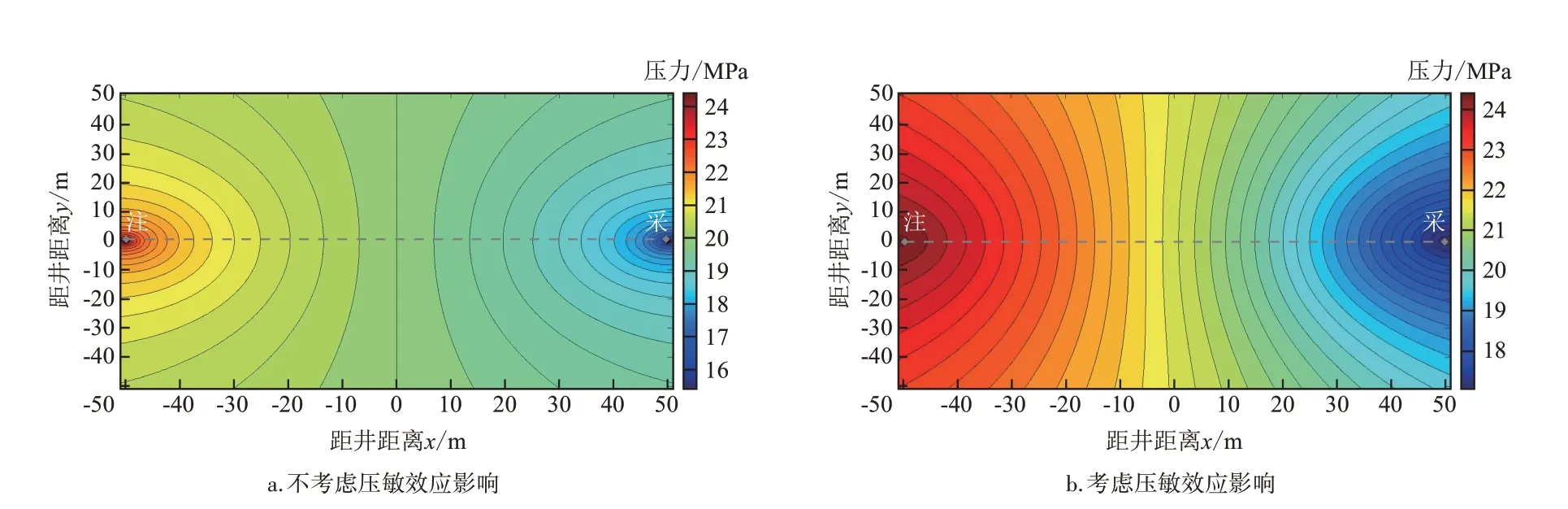
图2 有无压敏效应影响的注采压力场对比Fig.2 Comparison of injection-production pressure fields with/without pressure sensitive effect

图2 为有无压敏效应影响的注采压力场对比。色标中红色越深、反映相应的压力值越大；蓝色越深，反映相应的压力值越小，压力单位为MPa。

可以看出：不考虑压敏效应时，注采单元压力场等值线沿注采中间线左右对称，中间线处的压力等于20 MPa（原始地层压力）；当考虑压敏效应时油藏时，由于在油井压力下降区储层渗透率降低，该区域压力损耗增大，导致注采单元压力场等值线沿注采中间线左右不再对称。

根据注采单元中压力场分布，可以进一步分析不同条件下注采连线上的压力、渗透率变化规律，为油藏有效注采井距的确定奠定基础。

2.2 不同条件下注采井间压力分布变化

计算不同初始启动压力梯度和介质变形系数下（注采压差10 MPa、井距200 m 时），井间地层压力分布变化，结果如图3所示。

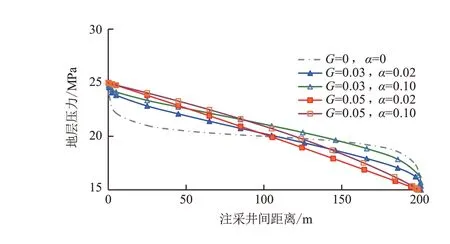
图3 不同条件下注采井间地层压力变化Fig.3 Formation pressure variation between injection-production wells under different conditions

在图3 中，坐标原点处为注水井点，横坐标右端200 m 处为生产井点。启动压力梯度G的单位为MPa/m，储层介质变形系数α的单位为MPa-1；其中G＝0、α＝0，表示储层中没有启动压力梯度和压力敏感的影响，作为基准对比条件。

从图3可以看出：不考虑启动压力梯度和压力敏感影响时，主流线上压力分布呈“S 形曲线”形态；启动压力梯度增大，会使“S 形曲线”形态特征减弱，逐渐变为线性；储层介质变形系数增大，会使井间压力曲线提升，且生产井附近压力升高值高于注水井附近压力升高值。

地层压力变化后，由于压力敏感的影响，储层渗透率相应发生变化，井间地层渗透率分布变化结果如图4 所示。其中，渗透率变化幅度K/K0，表示随压力变化后的渗透率K与储层初始渗透率K0的比值。

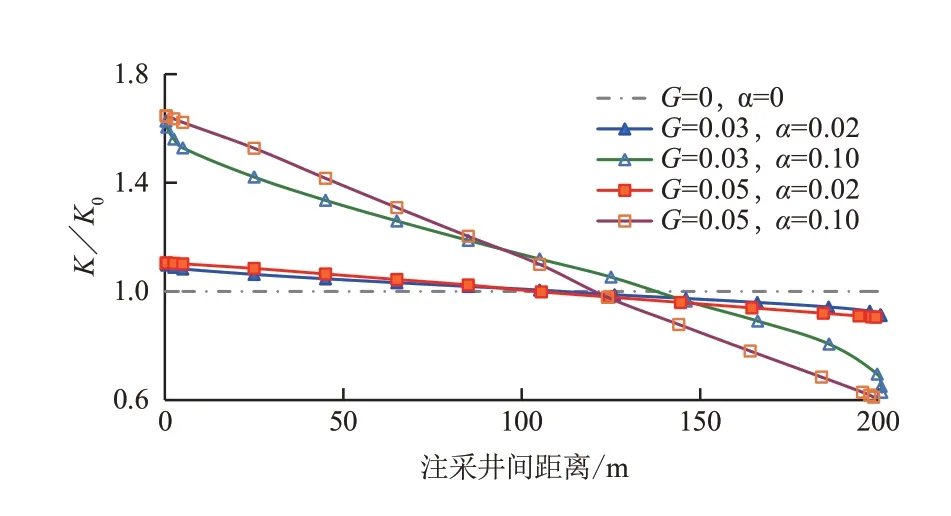
图4 不同条件下注采井间渗透率变化Fig.4 Permeability variation between injection-production wells under different conditions

从图4 可以看出：不考虑压力敏感影响时，地层渗透率保持不变。考虑压力敏感影响时，生产井区域压力下降，压力敏感影响使得生产井附近地层渗透率下降；注水井区域压力升高，注水井附近地层渗透率提高；且介质变形系数越大，注水井对地层渗透率提高的影响距离越远，生产井使地层渗透率下降的影响距离越短，“S形曲线”形态特征越强。当介质变形系数较小时，启动压力梯度对渗透率变化的影响较小；介质变形系数较大时，启动压力梯度越高，渗透率分布的线性规律越强。

2.3 不同条件下产量与注采井距变化

考虑不同条件下，油田产量与注采井距的变化关系曲线，如图5所示。其中启动压力梯度为0.03 MPa/m、储层介质变形系数为0.02 MPa-1作为计算示例取值。

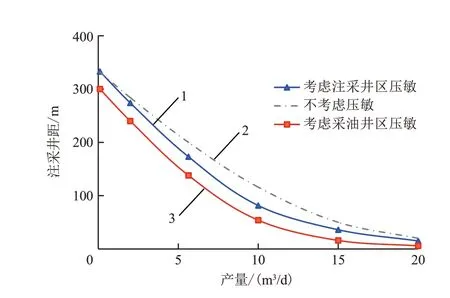
图5 不同条件下注采井距与产量变化Fig.5 Injection-production well spacing and production yield variation under different conditions

其中，曲线1 考虑注采井区压力敏感影响，表示综合注水井区压力升高、采油井区压力下降，引起相应区域储层渗透率和启动压力梯度变化带来的影响；曲线2 不考虑压力敏感影响，表示区域储层渗透率和启动压力梯度没有变化；曲线3考虑采油井区压力敏感影响，表示只考虑采油井区压力下降，引起相应区域储层渗透率和启动压力梯度变化带来的影响。

从图5可以看出：注采井距与产量呈非线性变化关系，不同条件下曲线的变化趋势相仿；不考虑压力敏感影响时，在相同产量要求下，计算的注采井距最大；只考虑采油井区压力敏感时，由于只有采油井区渗透率下降的影响，计算注采井距最小；而综合考虑注水井区、采油井区压力敏感影响，能够最接近真实反映注采开发过程中的变化，得到的注采井距最为合适。

以同时考虑注采井区压力敏感影响计算结果为基准，相比不考虑压力敏感影响、只考虑采油井区压力敏感影响，在同等条件和产量下，注采井距计算结果差别分别为+9.8%、-20.6%。

对比产量变化可以进一步推论压力敏感油藏合理开发策略：应实施早期、同步注水，油藏地层压力应尽可能保持在原始地层压力水平上；制定合理生产压差，以避免压力下降范围内出现较大的介质变形（渗透率明显下降），而造成较大的产能损失。

3 XC油藏有效注采井距的确定

根据上述方法，基于目标油藏实际情况，计算满足开发要求的有效注采井距，作为油藏开发井网部署的依据。所谓有效注采井距，就是满足油田单井最小产能（产量）要求，可以实现收支平衡时对应的注采井距。

XC 低渗油藏储层渗透率为3.58×10-3µm2，地下原油黏度为3.2 mPa·s，原始地层压力为20.0 MPa，设计开发方案中储层有效厚度为40 m；测试原始启动压力梯度为0.03 MPa/m，储层介质变形系数为0.02 MPa-1；考虑压力敏感的影响，初期注采压差为10 MPa，后期可适当放大。

综合考虑注水井区、采油井区压力敏感带来的影响，计算不同初始启动压力梯度和介质变形系数下，油井日产量（产能）与注采井距之间的变化关系，结果如图6所示。

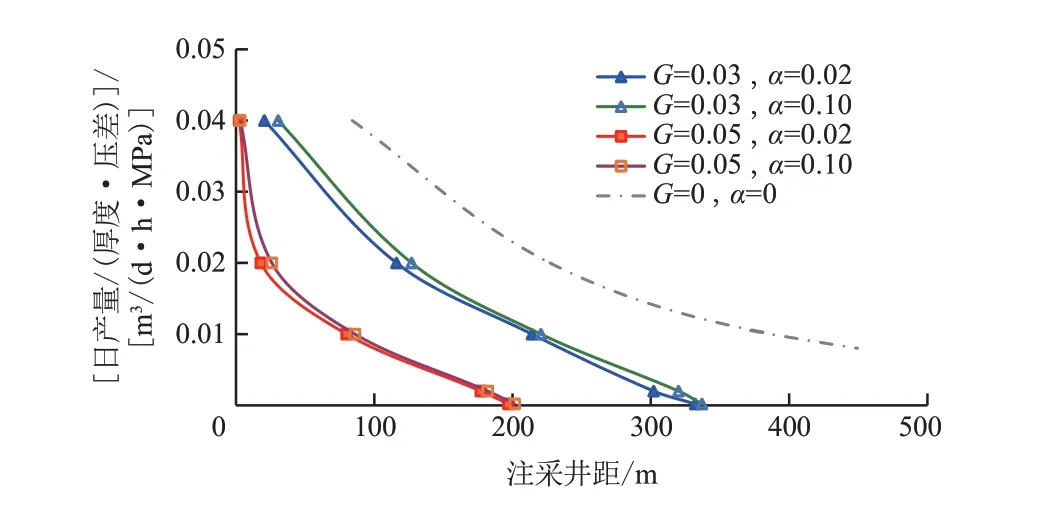
图6 不同条件下生产能力变化曲线Fig.6 Curve of production capacity under different conditions

为消除有效厚度、注采压差取值大小的影响，图6纵坐标为单位厚度下的产能Q/（Δph），等于单位厚度、单位注采压差下的产量。

从图6 可以看出：随注采距离增大，油井单位厚度下的产能呈非线性降低的态势，不同启动压力梯度、储层介质变形系数下的变化规律相仿。与不考虑启动压力梯度和压力敏感影响相比，启动压力梯度的影响显著；启动压力梯度越大，产能降低幅度越大。由于注水井处压力升高的作用，随着储层介质变形系数的增大，在相同注采距离下，产能略有增大。

当单位厚度下产能为0时，对应的开发井距为极限注采井距；当油田对经济极限产能有不同要求时，通过图6可得到相应的有效注采井距。对于目标XC油藏，产量为0 时极限注采井距约为330 m，当要求经济极限产能为0.01 m3/（d·h·MPa）时（实际初始油井产量为4.0 m3/d），相应有效注采井距为210 m左右。

考虑产量界限要求确定的有效注采井距，明显小于极限注采井距，一般条件下（原始启动压力梯度小于0.03 MPa/m，储层介质变形系数小于0.02 MPa-1），在单位厚度下产能界限小于0.01 m3/（d·h·MPa）时，有效注采井距约为极限注采井距的0.7～0.9倍。

4 结论

1）基于经典渗流理论建立了综合考虑启动压力梯度和压力敏感影响的典型注采井渗流方程，求解得到不同条件下注采井间压力变化规律，研究表明，启动压力梯度的增强会使注采井间压力分布的“S 形曲线”形态特征减弱，线性特征增强，注采井间的压力敏感效应会使井间压力变化曲线抬升，随着储层介质变形系数的增大，注水井影响范围增大。

2）综合考虑注水井区、采油井区压力敏感影响，能够最接近真实反映注采开发过程中的变化，得到的注采井距最为合适。以同时考虑注采井区压力敏感影响计算结果为基准，相比不考虑压力敏感影响、只考虑采油井区压力敏感影响，在同等条件下，注采井距计算结果差别分别为+9.8%、-20.6%。

3）对于给定产量要求的有效注采井距，相比于极限注采井距可以更好地指导低渗压力敏感油藏开发井网的合理部署，一般条件下有效注采井距约为极限注采井距的0.7～0.9倍。实例应用表明，方法简便有效、可操作性强。