考虑重力作用的垂向双洞窜流试井模型
徐燕东,陶杉,何辉,万小勇,邹宁,袁鸿飞
(1.中国石化西北油田分公司,新疆 乌鲁木齐 830011;2.中国石化碳酸盐岩缝洞型油藏提高采收率重点实验室,新疆 乌鲁木齐 830011;3.西安华线石油科技有限公司,陕西 西安 710065)
顺北油气田位于塔里木盆地顺托果勒低隆北部,油气资源丰富,属于断控岩溶背景的缝洞型碳酸盐岩油气藏[1-2]。顺北断溶体油藏垂向深度深,储层结构复杂,且具有很强的非均质性[3-5]。试井分析作为油气藏动、静态资料评价的重要方法,在此类油气藏中具有广泛应用[6-7]。
对于缝、洞连续分布且尺度较小的缝洞型油气藏[8],普遍使用以达西定律和连续性假设为基础的WARREN-ROOT 双重孔隙介质模型[9]以及在此基础上改进和扩展的多重孔隙介质模型[10-11]。而针对大尺度的缝洞型油气藏,一些学者认为缝洞中流体具有极高的流动性,压力可以瞬间传到溶洞边界并形成拟稳态流,由此建立了不同缝洞组合关系的等势体缝洞试井解释模型。刘洪等[12]和尹洪军等[13]建立了井钻遇溶洞试井解释数学模型,其中溶洞为等势体模型,溶洞外储层为双重孔隙介质模型。彭小龙等[14]、常宝华等[15]和段宝江等[16]建立了大尺度溶洞裂缝型油藏等势体试井分析模型,其中裂缝考虑为一维拟稳定流模型。熊钰等[17]根据地质特征,建立了井打在大尺度裂缝上的缝洞型试井模型和串联双洞型试井模型,实例解释结果与地质模型和钻井数据有着较好的一致性。
少数学者在大尺度缝洞型油气藏的试井解析理论研究中考虑了重力因素。徐燕东[18]结合顺北油田断溶体储层纵向分布深的特征,建立了考虑重力因素的断溶体储层“井-洞-缝”试井模型。马国锐等[19]将溶洞与裂缝组合系统视作联立的圆柱形区域,建立了一种考虑重力因素影响的单洞型断溶体储层试井解释方法。DU 等[20]综合考虑了流动和波动对溶洞压力变化的影响,建立了波动与流动耦合方程,进一步将重力作用修正到附加压降中并结合外部地层渗流方程形成了新的缝洞型油藏试井模型。
综上所述,在缝洞型油气藏的解析试井模型研究中,普遍忽略了重力因素的影响。少数学者在断溶体储层试井模型中考虑了重力作用,模型种类较少,仍需扩充完善,以便更好地适用于复杂地质特征。针对顺北油气藏缝洞储层垂向深度深的特征,建立了考虑重力作用的双洞窜流试井模型。利用Laplace 变换方法对模型进行解析求解,并给出部分参数变化的典型特征图以及应用实例。
1 试井解释模型
1.1 模型假设
大溶洞1 和大溶洞2 均为圆柱体,分别位于圆形封闭储层1和储层2中心,直井钻遇大溶洞1,产量恒定;大溶洞1 和2 在储层纵向分布,通过窜流通道连接,大溶洞具有无限导流能力(等效压力点分别取在大溶洞1 和2 的中部位置),流体在窜流通道中的流动为非稳态流;储层1、2是由小尺度裂缝构成的裂缝性储层,流体流动符合达西渗流;储层1、2 之间无流体交换,并分别向大溶洞1、2 供给流体,大溶洞2 中流体通过窜流通道流入大溶洞1,总系统中流体都经大溶洞1 流入井筒;岩石及流体微可压缩,且压缩系数为常数;考虑溶洞储集效应,考虑重力作用(图1)。

图1 物理模型示意图Fig.1 Physical model diagram
1.2 数学模型
根据渗流理论可建立储层1控制方程:
式中无因次变量的定义如下:
式中:p1D为储层1无因次压力;rD为无因次径向距离;tD为无因次时间;k1为储层1 渗透率,单位10-3µm2;h1为储层1 厚度,单位m;q为流量,单位m3/d;μ为黏度,单位mPa·s;B为体积系数,单位m3/m3;pi为初始压力,单位MPa;p1为储层1 压力,单位MPa;r为径向距离,单位m;L为参考长度(通常以井径作为参考),单位m;t为时间,单位h;φ1为储层1孔隙度;Ct1为储层1综合压缩系数,单位MPa-1。
储层2控制方程:
式中无因次变量的定义如下:
式中:p2D为储层2 无因次压力;σ21为储层2 与储层1的导压系数比;p2为储层2 压力,单位MPa;k2为储层2 渗透率,单位10-3µm2;φ2为储层2 孔隙度;Ct2为储层2综合压缩系数,单位MPa-1。
窜流通道控制方程:
式中无因次变量的定义如下:
式中:pfD为窜流通道无因次压力;zD为无因次垂向距离;cD为流体压缩系数与无因次压力转换系数的比值;gD为考虑重力作用时的无因次附加压力;σf1为窜流通道与储层1 的导压系数比;pf为窜流通道压力,单位MPa;kf为窜流通道渗透率,单位10-3µm2;φf为窜流通道孔隙度;Ctf为窜流通道综合压缩系数,单位MPa-1;CL为流体压缩系数,单位MPa-1;ρ为流体的密度,单位kg/m3;g为重力加速度,单位m/s2;z为垂向距离,单位m。
根据物质守恒及窜流通道与大溶洞1 连接处压力相等条件:
式(4)—式(5)中无因次变量的定义如下:
式(4)—式(5)中:pv1D为溶洞1 无因次压力;rv1D为溶洞1 无因次半径;rfD为窜流通道无因次半径;hv1D为溶洞1 无因次中心点高度;h2D为储层2 无因次厚度;ωv1为溶洞1 储容比;LfD为窜流通道无因次长度;mf1为窜流通道与储层1 的流度比;pv1为溶洞1 压力,单位MPa;rv1为溶洞1半径,单位m;rf为窜流通道半径,单位m;hv1为溶洞1 中心点高度,单位m;h2为储层2厚度,单位m;Lf为窜流通道长度,单位m;Ctv1为溶洞1综合压缩系数,单位MPa-1;φv1为溶洞1孔隙度。
根据物质守恒及窜流通道与大溶洞2 连接处压力相等条件:
式(6)—(7)中无因次变量的定义如下:
式(6)—(7)中:pv2D为溶洞2 无因次压力;rv2D为溶洞2 无因次半径;hv2D为溶洞2 无因次中心点高度;ωv2为溶洞2 储容比;m21为储层2 与储层1 的流度比;pv2为溶洞2 压力,单位MPa;rv2为溶洞2 半径,单位m;hv2为溶洞2中心点高度,单位m;Ctv2为溶洞2综合压缩系数,单位MPa-1;φv2为溶洞2孔隙度。
储层与溶洞连接条件:
储层外边界条件:
式(8)—式(10)中无因次变量的定义如下:
式(8)—式(10)中:re1D为储层1无因次半径;re2D为储层2 无因次半径;re1为储层1 半径,单位m;re2为储层2半径,单位m;。
系统考虑重力时,储层、溶洞以及窜流通道中初始时刻的压力均是垂向距离z的函数:
式中:下标1,2,v1,v2,f分别表示储层1、储层2、溶洞1、溶洞2、窜流通道。
1.3 模型求解
基于tD对式(1)—式(11)作Laplace变换,并结合初始条件和边界条件求解可得Laplace 空间井底压力解为:
式(12)—式(19)中:u为无因次时间tD对应的Laplace变量;I0、K0分别为改进的零阶第一类修正贝塞尔函数和零阶第二类修正贝塞尔函数;I1、K1分别为改进的一阶第一类修正贝塞尔函数和一阶第二类修正贝塞尔函数;CfD、f1、f2、b1、b2、bf1、bf2均为中间变量。
2 典型图版及参数敏感性分析
2.1 典型图版
图2 为无因次压力降落典型曲线。根据其特征可分为9 个响应段:①大溶洞1 拟稳态流段,由于溶洞1的储集效应,无因次压力及其导数曲线前期基本呈斜率为1 的直线;②窜流通道线性流与储层1 径向流叠加响应段,无因次压力及其导数曲线斜率介于0~0.5;③大溶洞2 过渡流与储层1 径向流叠加响应段,溶洞2 流体通过窜流通道进入溶洞1,无因次压力导数曲线缓慢下降;④大溶洞2 拟稳态流与储层1径向流叠加响应段,由于溶洞2 的储集效应,无因次压力导数曲线缓慢上升;⑤储层1 径向流和储层2 径向流叠加响应段,无因次压力导数曲线后端基本呈水平线;⑥储层1 拟稳态流段,压力波传播至储层1边界,储层1 的供给作用逐渐减弱,无因次压力导数曲线开始上翘;⑦储层2 过渡流段,储层2 的供给作用逐渐增强,无因次压力导数曲线下掉;⑧储层2 径向流段,无因次压力导数曲线后端基本为水平线;⑨储层2 拟稳态流段(封闭边界控制流段),储层2 的供给作用逐渐减弱,无因次压力导数曲线上翘,后期基本呈斜率为1的直线。
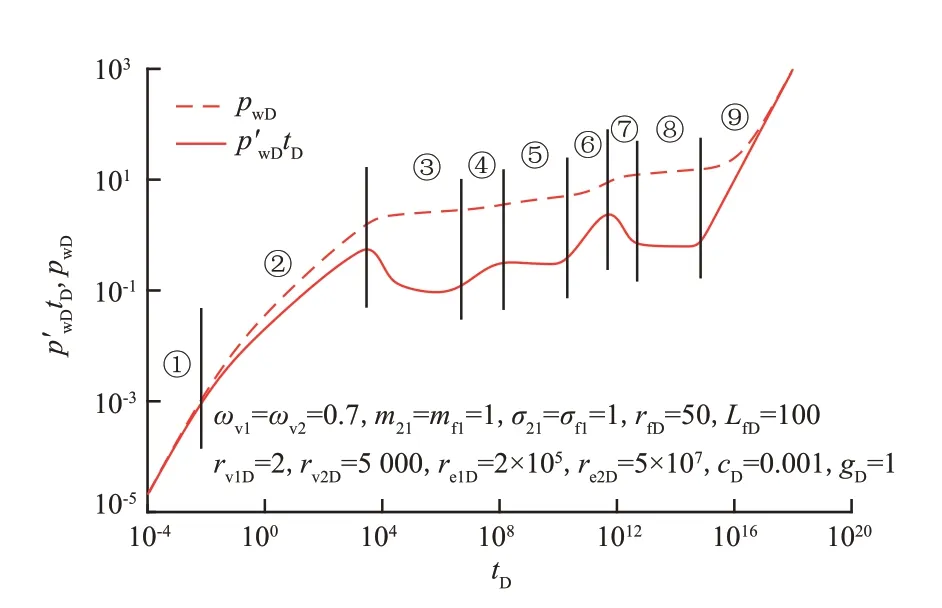
图2 无因次压力降落典型曲线Fig.2 Typical curve diagram of dimensionless pressure drop
图3 为不考虑小尺度裂缝储层渗流作用的无因次压力降落典型曲线(令储层1 的半径等于溶洞1 的半径以及储层2 的半径等于溶洞2 的半径即可实现)。典型特征图可分为4 个响应段:①大溶洞1 拟稳态流段,无因次压力及其导数曲线前期基本呈斜率为1 的直线;②窜流通道线性流响应段,无因次压力及其导数曲线斜率基本呈斜率为0.5 的平行线;③大溶洞2过渡流响应段,无因次压力导数曲线出现快速下掉;④大溶洞2 拟稳态流响应段,无因次压力导数曲线呈斜率为1的直线。
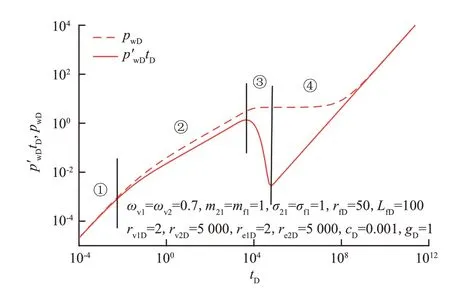
图3 无因次压力降落典型曲线(不考虑小尺度裂缝储层渗流作用)Fig.3 Typical curve of dimensionless pressure drop(without considering the flowing effect of small-scale fractured reservoir)
2.2 参数敏感性分析
图4 为考虑重力作用时的无因次附加压力变化响应特征。无因次附加压力主要对无因次压力降落图的中期及后期影响较大。当无因次附加压力越大时,流体受重力影响越大,系统中流体流动需要克服的阻力也越大,相应的无因次压力及其导数曲线位置也越高。
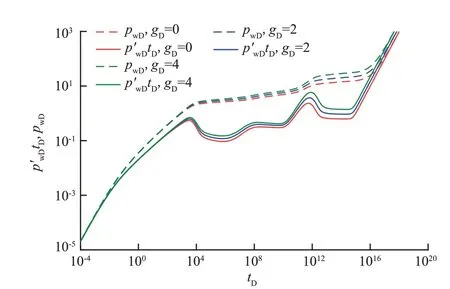
图4 无因次附加压力变化响应特征Fig.4 Response characteristic diagram of Dimensionless additional pressure change
图5 为窜流通道无因次长度变化响应特征。窜流通道无因次长度主要对无因次压力降落图的中期影响较大。窜流通道无因次长度增大时,窜流通道线性流与储层1 径向流叠加响应持续时间延长。同时,流体通过窜流通道时间增加,消耗能量增多,由溶洞2及储层2流向溶洞1的阻力增大,因此,相应的无因次压力及其导数曲线位置靠上。
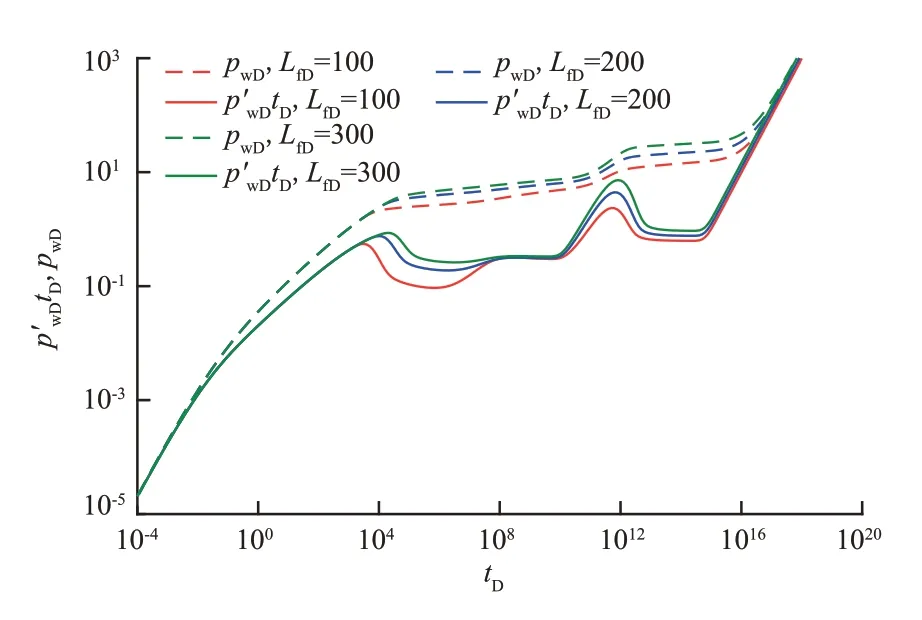
图5 窜流通道无因次长度变化响应特征Fig.5 Response characteristic diagram of dimensionless length change of channeling channel
图6为溶洞1无因次半径变化响应特征。溶洞1无因次半径主要对无因次压力降落图的前期影响较大。溶洞1 无因次半径越大,溶洞体积越大,所具有的弹性能量越大且储存流体越多,因此,拟稳态流持续时间也越长。

图6 溶洞1无因次半径变化响应特征Fig.6 Response characteristic diagram of dimensionless radius change of cave 1
图7为溶洞2无因次半径变化响应特征。溶洞2无因次半径主要对无因次压力降落图的中期影响较大。溶洞2 无因次半径越大,溶洞体积越大,所具有的弹性能量越大且储存流体越多,因此,溶洞2 拟稳态流与储层1径向流叠加响应持续时间越长,导数曲线上翘特征出现越晚。
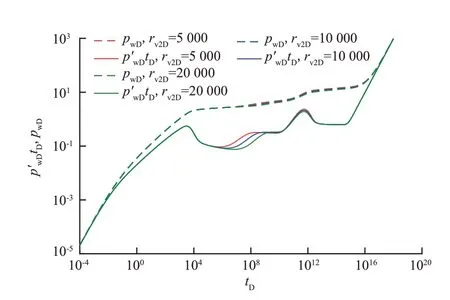
图7 溶洞2无因次半径变化响应特征Fig.7 Response characteristic diagram of dimensionless radius change of cave 2
3 实例分析
X 井为顺北油田5 号断裂带上的一口开发井,钻井过程中漏失1 400 kg/m3的泥浆25.45 m³,酸压投产后随即进行关井压力恢复测试。关井测试前7 mm油嘴日均产油量约为326.0 m3,等效稳产时间113.2 h,关井有效测试时间为251.0 h。油体积系数1.58 m3/m3,油黏度0.33 mPa·s,储层综合压缩系数3.17×10-3MPa-1,孔隙度0.1,测试井段储层1 有效厚度10.0 m。实测恢复压力差及其导数曲线如图8所示,前端无明显的线性流与经向流叠加特征,表明窜流通道的导压系数可能较大,很快地达到拟稳态流阶段。前期下凹段持续时间相对较长,表明溶洞2 和储层1 的储集体规模不大。后期导数曲线缓慢下掉主要是因为测试前生产时间相对较短,未探及储层2 的边界所致(若探及储层2的边界,则导数曲线会快速下掉)。

图8 顺北油田X井拟合成果Fig.8 Fitting results diagram of X well in Shunbei oilfield
结合测试前高产、钻井漏失以及实测数据双对数曲线图的特点,应用模型对该实例井进行拟合分析,解释结果为:储层1 渗透率6.58×10-3µm2,大溶洞1半径4.2 m,大溶洞2 半径18.21 m,储层1 外边界60.00 m,窜流通道长度30.20 m,拟合压力80.355 MPa。同时,应用商业软件Saphir中的径向两区复合模型进行拟合分析,解释结果为:井储系数0.59 m3/MPa,表皮因子-4.20,内区渗透率293.79×10-3µm2,内区边界31.72 m,拟合压力80.394 MPa。对比发现,从拟合效果(图8)上来看,垂向双洞窜流模型与Saphir 的径向两区复合模型拟合效果均较好,但结合现场地质背景情况,径向两区复合模型明显不符合使用条件,垂向双洞窜流模型能较好反应储层特征。因此,选用垂向双洞窜流模型解释的结果与现场生产动态情况也更为吻合,可靠性相对更高。
4 结论
建立了考虑重力作用的大尺度缝洞试井模型,应用数学物理方法对模型进行解析求解并绘制了模型典型特征图版及参数敏感性分析图版,给出了应用实例,主要结论如下:
1)考虑重力作用时,流体流动需要克服更大的阻力,因此无因次压力及其导数曲线中期及后期位置更高,表明考虑重力作用的必要性。总体曲线特征和不考虑重力作用相似。
2)考虑小尺度裂缝储层渗流作用时,窜流通道线性流与储层径向流叠加特征表现为无因次压力及其压力导数曲线斜率介于0~0.5。大溶洞过渡流与径向流叠加特征表现为无因次压力导数曲线缓慢下降。大溶洞拟稳态流与径向流叠加特征表现为无因次压力导数曲线缓慢上升且斜率小于1。
3)不考虑小尺度裂缝储层渗流作用时,窜流通道线性流特征表现为无因次压力及其压力导数曲线斜率接近0.5。大溶洞过渡流特征表现为无因次压力导数曲线快速下掉。大溶洞拟稳态流特征表现为无因次压力导数曲线斜率接近1。

