基于T-LSTM 模型的线路故障诊断方法及迁移性研究

吴俊宏，张 印，李 莎，周 杰，吴 松，王金磊

（雅砻江流域水电开发有限公司二滩水力发电厂， 四川 攀枝花 617000）

目前将深度学习技术引入电力线路故障诊断领域已经取得了一定的成效[1]。然而，对深度学习模型进行训练需要用到大量的故障数据，如果用于训练的故障数据不能满足要求，将会导致模型的性能严重下降[2]。近年来，随着深度学习的广泛应用，迁移学习也受到了越来越多的关注[3]。迁移学习可以把深度学习模型在某一领域中学习到的知识迁移到另一相关领域中，这样可以使深度学习模型在数据不足的情况下仍能在新领域具备良好的性能[4]。为了使训练出的LSTM 故障诊断模型具有良好的可迁移性，本文将结合迁移学习的理论和LSTM 深度学习模型，提出了基于迁移LSTM（T-LSTM）模型的电力线路故障诊断方法。

1 迁移学习相关理论

在现实生活中，想要获取如此多数量的带标注的数据是十分困难的，即使能够获取，也需要花费大量的人力物力。除此之外，不同应用场景下的数据分布是存在一定差异的，想要用一个通用的深度学习模型来满足不同应用场景下的使用需求是非常困难的。即使拥有足够用于训练的标注数据，但是要从头训练一个复杂的深度网络模型是十分耗时的。因此，为了解决标注数据缺乏、数据分布差异和训练过程耗时的问题，提出了迁移学习的概念。在迁移学习中，对“域”和“任务”的数学定义分别如式（1）和式（2）所示：

式中，x表示域中样本的特征空间，P（X）表示边际概率分布，其中，X满足X={x1，x2，...，xn}∈x；y代表标签空间，f（g）为目标预测函数。

所谓的迁移学习，就是将深度学习模型从一个或者多个源域Ds的任务Ts中学习和提取到的有用知识和经验用在新的目标域DT的任务TT上。简单来说，就是将对于某一个问题训练好的模型通过对其进行简单地调整，使其同样能够在一个新的问题上表现出良好的性能。

2 源线路与目标线路故障数据的相似性计算

当对模型进行迁移学习时，其中一个关键的问题就是负迁移。负迁移不仅不会对迁移模型在目标域任务上的表现有任何帮助作用，反而会影响其在目标域任务上所表现出的性能。因此，在进行迁移学习之前，对源域数据和目标域数据的分布进行相似性计算是非常有必要的。

本文将用来对模型进行预训练的线路称为源线路，将应用迁移训练后的模型进行故障诊断的线路称为目标线路。为了检验源线路与目标线路故障数据分布之间的相似性，本文使用最大均值差异（MMD）的方法来计算源线路与目标线路故障数据分布之间的相似性。然后，选取与目标线路故障数据相似性最大的源线路对应的预训练模型，并对其进行迁移训练。

对于一个满足p分布的样本集X={x1，x2，...，xn}和一个满足q分布的样本集Y={y1，y2，...，yn}，通过寻找在样本空间上的映射函数f，计算出两个分布的样本在函数f上的均值，通过将两个均值相减，即可求出两个分布对应于f的均值差异。当找到某一个f使得这个均值差异有最大值时，就得到了MMD 值。MMD 的计算表达式如式（3）所示：

式中，sup（g）表示求上界，Ex～p和Ey～q表示均值，F表示在样本空间上的函数集合。

设源线路的故障样本和目标线路的故障样本分别对应分布p和q，X和Y则分别表示从源线路和目标线路上采集得到的两个短路故障数据集，数据集的大小分别为m和n。可以得出MMD 的经验估计表达式如式（4）所示：

V'MMD[X，Y]的值越小，就表示源线路的故障数据和目标线路的故障数据分布相似性越大，当V'MMD[X，Y]=0 时，则表示两个数据集来自同一分布。反之，当V'MMD[X，Y]的值越大时，则表示源线路的故障数据和目标线路的故障数据分布差异越大。

3 基于T-LSTM 的故障诊断方法

3.1 基于LSTM 模型的故障诊断方法

在对线路故障诊断的研究中，本文提出了基于LSTM 深度网络模型的故障诊断方法[5]。用于线路故障诊断的LSTM 深度网络模型的结构见图1。

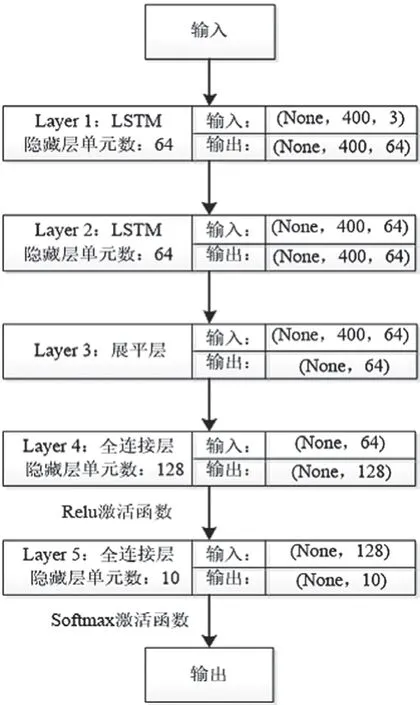
图1 LSTM 深度网络模型的结构

该模型包含了2 个具有64 个隐藏单元的LSTM层。在LSTM 层后设置了一个展平层，用于从LSTM层到全连接层的过渡。展平层可以获取LSTM 层最后一个记忆单元的输出并将其平铺成一维向量。在展平层后设置隐藏单元为128 的全连接层，使用ReLU函数作为该层的激活函数。最后使用一个隐藏单元为10 的全连接层作为分类层，使用Softmax 函数作为激活函数输出0 到1 的值，实现对线路故障的诊断。

在深度网络模型的训练过程中，对于有q个样本的训练集，将前向传播迭代输出的向量Y'i与故障样本真实的标签向量Yi的均方误差值作为损失函数的函数值J，其计算公式如式（5）所示。

然后，使用基于梯度下降的Adam 优化算法[6]，将损失值和损失函数的梯度反馈到网络以更新权重和偏差，从而达到训练深度网络的目的。

为保证训练时网络能够更好的收敛到最优值，这里使用指数衰减学习率[7]，使学习率随着训练的迭代轮次增加而减小，其表达式如式（6）所示：

其中：η0表示初始学习率；RD为衰减率；NB为一个训练批次中的样本数；ST为训练迭代的轮次；q为训练集总的故障样本数；η表示经过ST轮训练后的学习率。

其训练和验证过程中损失值与正确率的迭代图如图2 所示。

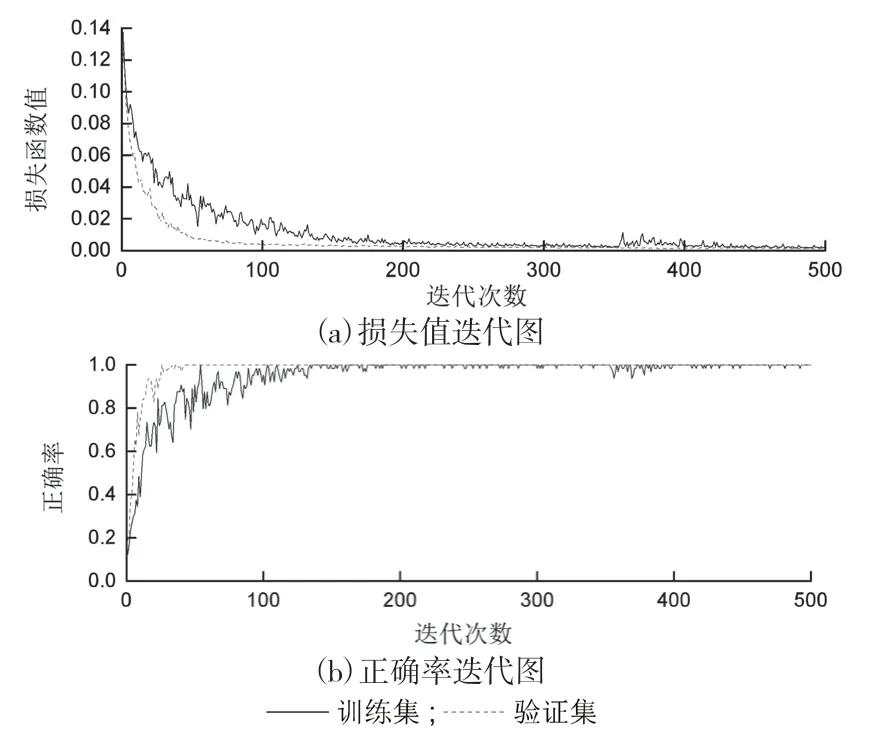
图2 模型训练过程中的损失值与正确率迭代图

从图2 中可以看出，算法在训练集和验证集上的损失值均在下降，故该模型没有出现过拟合的现象。此外，在经过500 个迭代周期的训练后，总体的识别准确率均可以稳定在100%。

3.2 T-LSTM 故障诊断模型的理论框架

根据迁移学习的相关理论，本文在LSTM 模型的基础上，提出了使用经过迁移训练的LSTM（T-LSTM）模型来对输电线路短路故障进行故障诊断的方法。T-LSTM 故障诊断模型的原理框图如图3 所示。

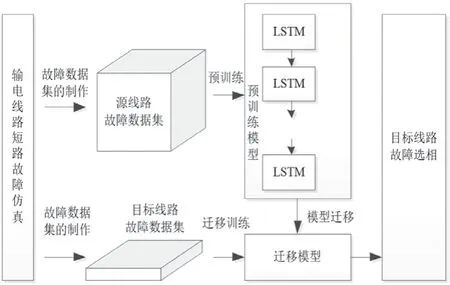
图3 T-LSTM 故障诊断模型的原理框图

根据图3 可知，基于T-LSTM 模型的故障诊断方法主要包含了以下3 个步骤：

（1）在仿真平台上搭建电力线路仿真模型，通过改变电力线路中的电压等级、线路长度和线路单位长度的电阻、电感、电容等参数，分别建立起源线路和目标线路的仿真模型。再分别对源线路和目标线路在不同工况下进行短路故障仿真，来分别获取源线路的故障样本和少量目标线路的故障样本，并将其制作成数据集；

（2）根据本文第2 节中所提到的方法计算每条源线路和目标线路的故障数据分布的相似程度，选择与目标线路相似度最大的源线路，并使用该源线路的故障数据集对LSTM 模型进行预训练，从而得到经过预训练后的LSTM 故障诊断模型；

（3）使用少量目标线路的故障样本来对经过预训练后的LSTM 模型进行迁移训练，来获得经过迁移训练过后的LSTM（T-LSTM）模型，并将T-LSTM模型用于对目标线路进行故障诊断。

4 实例验证及可迁移性分析

4.1 源线路与目标线路的故障数据生成

利用仿真平台搭建输电线路故障仿真模型，分别建立起源线路和目标线路的仿真模型。本文分别搭建了3 条源线路和1 条目标线路的仿真模型，每条输电线路的具体参数如表1 所示。

表1 源线路和目标线路的系统参数

根据表1 中的参数搭建起输电线路的仿真模型后，在各条源线路和目标线路的仿真模型上，对不同故障类型、不同故障位置、不同故障阻抗和系统两端电源不同相位差的各种参数组合进行故障仿真，来分别获取源线路的故障样本和少量目标线路的故障样本，并将其制作成故障数据集。这里采集的故障数据同样是故障发生后一个周期内三相故障电流序列，采样频率为20 kHz。

由于源线路和目标线路的故障数据分布存在一定的差异，为了防止在迁移训练的过程中出现负迁移的问题，使用本文第2 节所述的MMD 来计算每条源线路和目标线路故障数据分布的相似程度，选择与目标线路故障数据相似度最高的1 条源线路，并对使用该源线路故障样本预训练后的LSTM 模型进行迁移训练。

4.2 T-LSTM 模型的测试和微调率对性能的影响

在对LSTM 模型进行预训练的过程中，源线路的短路故障样本为1 350 组，目标线路的故障样本为540 组。由于本文中的3 条源线路和目标线路故障数据之间的MMD 值相近且数值较小，不存在负迁移的问题，故选择源线路L1的故障样本对模型进行预训练。在预训练模型的基础上，使用少量的目标线路的短路故障样本对模型进行迁移训练，最终得到T-LSTM 模型。并使用目标线路的测试集样本对T-LSTM 模型的性能进行测试。

在T-LSTM 模型的整个训练过程中，预训练的迭代次数设置为500，迁移训练的迭代次数设置为100。除此之外，迁移训练中使用的目标线路的故障样本数量会对模型最终的诊断准确率产生较大的影响。这里将用于模型迁移训练的目标线路故障样本数量与用于模型预训练的源线路故障样本数量的比值称为微调率。图4 展示了在不同的微调率下，T-LSTM 模型在目标线路的测试集上故障诊断正确率的变化情况。

图4 不同微调率下T-LSTM 模型诊断正确率的变化

从图4 中可以看出，当微调率为0 时，即没有对模型进行迁移训练时，模型在目标线路上的故障诊断正确率仅为81.11%。随着微调率的升高，T-LSTM模型的故障诊断准确率也随之得到提升。当微调率达到10%时，T-LSTM 模型在目标线路上的故障诊断正确率能够达到100%。由此可以得出，和没有经过迁移学习的LSTM 模型相比，T-LSTM 故障诊断模型具有更好的可迁移性，能够在新的目标线路的故障诊断问题上表现出更加良好的性能。

4.3 实例验证

为了更好地验证本文所提出的故障诊断模型在实际线路故障时的诊断准确率，这里使用了某大型水电站某线路发生单相接地故障时的故障录波数据对该故障诊断模型的性能进行验证。该线路发生故障时的故障录波波形如图5 所示。

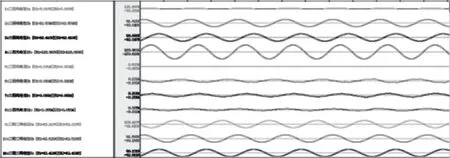
图5 某水电站线路发生单相接地故障时故障录波波形

截取该线路故障发生后一个周期内的三相电流信号作为故障特征信号，经过前向传播计算，故障诊断模型输出一个表示短路故障类型的多维向量。针对该线路的故障，经故障诊断模型计算后，输出的向量 为Y'=[0.99 0.00 0.00 0.00 0.00 0.01 0.00 -0.01 0.01 0.00]。其中，输出的十维向量Y'中，不同的数字代表该故障诊断模型将此故障诊断为10 种故障类型时分别对应的概率。

通过输出的向量可以看出，故障诊断模型将该线路故障诊断为A 相接地故障的概率为99%，因此，诊断该线路故障类型为A 相接地短路，与线路实际故障情况一致。

经过实例验证，该方法能够对实际电力线路的故障类型准确地进行诊断。

5 结论

本文阐述了基于T-LSTM 模型的故障诊断方法，并对其进行了可迁移性研究。首先，结合迁移学习的相关理论，提出了使用T-LSTM 模型来对目标线路进行故障诊断的方法。在对LSTM 模型进行迁移训练的过程中，提出了使用MMD 算法来对源线路和目标线路故障数据的相似性进行计算，选出与目标线路相似性最高的源线路所对应的预训练模型，并使用目标线路的训练集样本对其进行迁移训练。然后，使用目标线路的测试集故障样本对T-LSTM 模型进行测试。通过实验验证，当迁移训练的微调率为10%时，T-LSTM 模型在目标线路上的故障诊断正确率能够达到100%，并且能够对实际电力线路的故障进行准确地诊断；而当微调率为0 时，即没有对模型进行迁移训练时，传统的LSTM模型在目标线路上的故障诊断正确率仅为81.11%。因此，表明了在目标线路故障样本较少的情况下，T-LSTM 仅需少量目标线路的故障数据对预训练模型进行微调，即可构建适用于目标线路的故障诊断模型。