基于惯性传感器阵列的行人导航发展综述
罗 肖,刘 磊,曹立佳,2,3,王 喆
(1.四川轻化工大学 自动化与信息工程学院, 四川 自贡 643000; 2.人工智能四川省重点实验室, 四川 自贡 643000; 3.企业信息化与物联网测控技术四川省高校重点实验室, 四川 自贡 643000; 4.四川腾盾科技有限公司, 成都 610037)
0 引言
全球卫星导航系统(global navigation satellite system,GNSS)信号拒止下,完成行人导航的主要方法为惯性导航,但由于惯性传感器存在测量误差会使导航误差不断累积,严重影响导航精度[1-2]。基于惯性传感器阵列的行人导航系统,通过惯性传感器阵列与零速修正(zero velocity update,ZUPT)相结合,可以有效地抑制随机噪声偏置不稳定性[3],并抑止累积误差的积累[4]。还可以通过对传感器输出数据的检测实现故障检测和隔离的功能[5-6]。由此产生了不同构造的惯性传感器阵列与融合算法研究。
惯性传感器阵列类型分为陀螺仪阵列,加速度计阵列以及二者组合形成的阵列。加速度计阵列根据离心力与角速度二次方成比例关系[7],用加速度计可以估计物体的比力和角加速度。但估计角速度需要对角加速度进行积分,增加了额外的积分步骤[8-10]。陀螺仪阵列,通过对陀螺仪测量的角速度进行处理,达到抑制陀螺仪随机漂移测量误差的目的[11-16]。但陀螺仪阵列只能完成姿态角度的测量,不能完成导航系统的全部功能。综合二者的优点,陀螺仪与加速度计组合的阵列,成为惯性传感器阵列研究的重点。此外,对于某些配置的阵列,角加速度可以直接估计,利用传感器的空间分离,动态测量范围可以扩展到超出单个传感器的范围[17-18]。
如何将阵列中多个惯性测量单元(inertial measurement unit,IMU)的数据进行融合是整个导航系统的关键,数据融合问题主要是在GNSS/IMU组合导航的框架内进行研究的[19-20]。数据融合框架可以大致分为2类:估计域融合与观测域融合[21-22]。观测域融合先将传感器数据进行融合,因此,过滤器只能“观测”融合之后的输出数据。优点是运算量小,但也无法观测到单个IMU的误差特性。估计域融合将N个单独的局部状态估计器产生的状态估计和相应的协方差矩阵进行融合得到最终的估计结果。其相对于观测域融合可以观测到单个IMU的误差特性,但也增加了运算量。惯性导航在长时间的工作下,即使采用惯性传感器阵列对测量误差进行了抑制,但累计误差仍是很大的。所以引入零速修正算法对基于惯性导航具有十分重要的意义[23]。零速修正算法通过对加速度,角速度等进行检测对导航过程产生的累计误差进行修正[24-25]。
本研究对惯性传感器阵列的构造与数据融合以及修正算法进行讨论,组织结构为:第1节论述惯性传感器阵列的主要类型,重点介绍不同阵列的误差建模。第2节讨论惯性传感器阵列的两种主要融合框架。第3节介绍零速修正算法的构成,主要分析零速探测器的工作原理。第4节总结归纳了基于惯性传感器阵列的行人导航系统目前存在的问题和未来的发展趋势。
1 惯性传感器阵列的构成
1.1 加速度计阵列
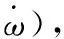
GF-IMU的模型来自于对经典刚体动力学的直观应用。科里奥利公式将刚体上任意离散点的加速度,与刚体整体的运动学联系起来,在由多个空间分离的加速度计组成的阵列中,不仅可以从加速度计的测量中提取关于平移运动的信息,还可以提取阵列的旋转运动。假设由N个微机电系统(micro electro mechanical systems,MEMS)组成的阵列,传感器是理想的,除了一个附加的测量噪声。如图1所示的MEMS阵列中的加速度计的测量值建模为

(1)
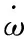
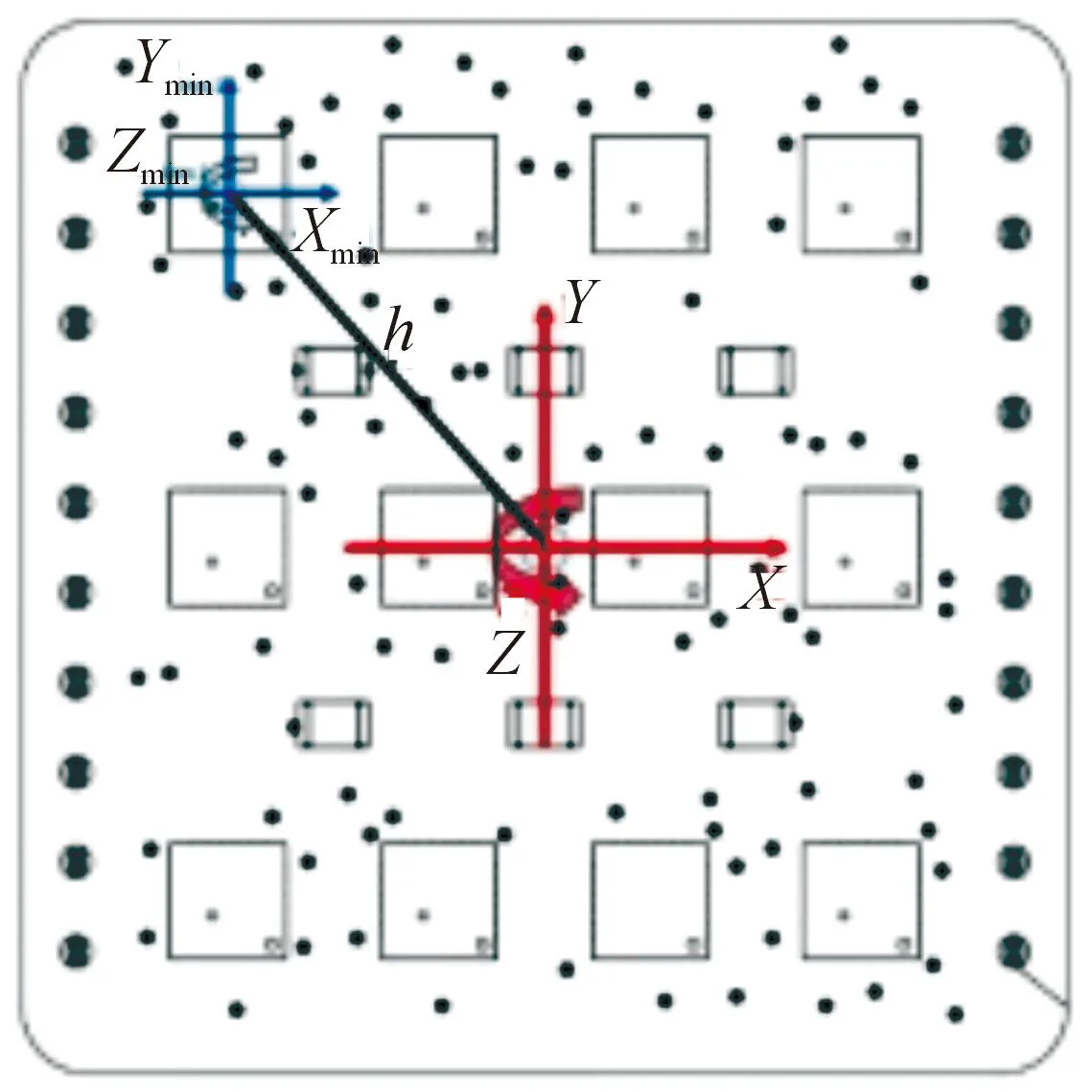
图1 MEMS阵列分布图
在加速度计阵列中角加速度还必须进行时间积分,以准确地估计角速度的大小[32],这增加了一个额外的时间积分步骤。给加速度计阵列提供了关于角速度和角加速度的信息,因此它在原则上可以取代陀螺仪进行方向估计。因为早期MEMS陀螺仪的性能低且能耗高,所以人们忽略了MEMS中陀螺仪的使用。然而,GF-IMU不能唯一地确定瞬时角速度,对于较低的动态旋转运动,角速度的估计误差是较高的[31]。
1.2 陀螺仪阵列
如何有效地抑止陀螺仪漂移是保证陀螺仪精度的关键所在。陀螺漂移一般分为系统漂移和随机漂移。通过使用适当的数学模型和漂移补偿计算,可以消除系统漂移对精度的影响。随机漂移是一个缓慢的时变弱信号,容易受到一些不确定因素的影响,如外部环境噪声等。因此,简单的随机漂移补偿方法是无效的。随机漂移误差包括漂移不稳定性、速率随机游走和角度随机游走。理论上,漂移不稳定性和测量的真实速率可以视为由白噪声驱动的随机游动过程[33]。在MEMS陀螺仪设计与制造过程中,如果要实现精度的显著提高,往往将会耗费大量的时间和经济成本。利用陀螺仪构成的阵列,采用信息融合技术对陀螺仪阵列进行处理,是降低陀螺仪的漂移噪声,提高精度的有效措施。可以采用一个具有代表性的陀螺仪随机误差模型来描述速率信号与陀螺仪输出之间的关系[12, 34-40]:
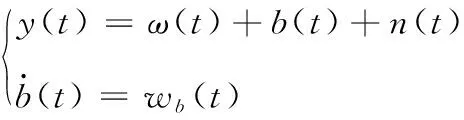
(2)
式(2)中:y表示陀螺仪的输出;ω表示角速度信号;b表示由速率随机游动wb引起的偏置偏移;n是角度随机游动的白噪声。给定一个有N个传感器的陀螺仪阵列,该陀螺仪阵列的模型可以写为

(3)
其中
然而,陀螺仪阵列只能量化和减轻测量误差的影响[41-45],如果要完成惯性导航功能,仍需加入加速度计。
1.3 加速度计和陀螺仪阵列
由加速度计和陀螺仪组成的阵列,将不再严格要求传感器的数量和配置方式,且可以解决加速度计阵列角速度正负方向模糊的问题,但如何将阵列中的传感器测量信息进行融合成为了研究的重点。特别是在由相同型号的加速度计和陀螺仪组成的阵列中,加速度计之间的距离可以忽略不计,测量误差可以被量化和减小其影响[46]。由不同量程的陀螺仪构成的阵列,可以扩大阵列的量测范围和测量精度[47]。增加陀螺仪后,额外的积分步骤将可能增加一个数量级,这对于加速度计和陀螺仪阵列的某些配置形式,产生的非线性常微分方程(ODE)可能是不稳定的[48],这个问题可以通过将加速度计置于复杂的配置形式中来解决[49]。针对如何将阵列中的传感器信息进行融合的问题,2016年Skog等提出了一种最大似然(ML)估计器[31],通过最大似然估计将多个传感器的测量值进行了融合。2022年Skog等提出了4种不同的状态空间模型,使用不同的基本假设,通过仿真和实际实验,利用李群扩展卡尔曼滤波对模型进行了评价[50]。通过融合加速度计和陀螺仪的测量值,可以显著降低测量误差,提高导航精度。此外,测量精度还与阵列的几何形状与传感器的配置方式有关,可以利用Skog提出的Cramér-Rao bound计算方法来提高[31]。
2 惯性传感器阵列信息融合
2.1 信息融合方法
多惯性传感器阵列数据融合方法可以分为2类:观察域融合和估计域融合[19, 31]。观测域融合将多个惯性传感器的测量值通过加权求和的方式融合为一个测量值。采用传统的单个IMU传感器估计器,并将其估计值作为数据融合的估计值。这是惯性传感器阵列数据融合问题的最常用的方法,也是目前研究最为广泛的方法[19]。这种方法的不足是当传感器具有不同的规格且需要精确的定时,很难解释单个传感器的偏差和误差特性。图2为观察域融合原理图。
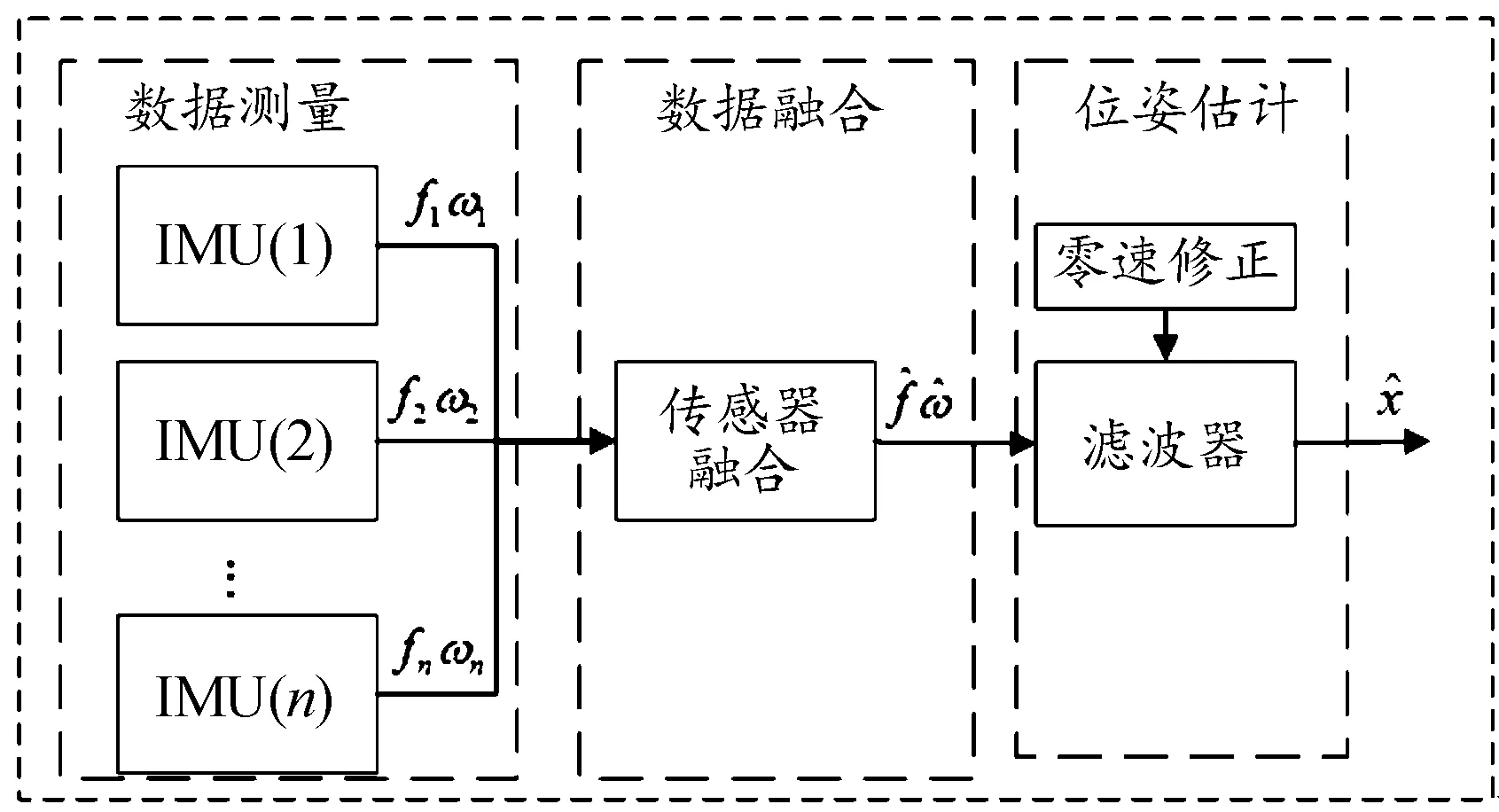
图2 观察域融合原理图
估计域融合,也被称为状态空间域中的融合,它将从多个子滤波器得到的位置姿态估计合并为一个状态的估计。如图3估计域融合原理图。

图3 估计域融合原理图
估计域的主要优点是,每个传感器的统计量和误差特征可以单独解释,因为每个估计已经对每个局部滤波器中的偏差和其他误差进行了修正。多个IMU的估计域融合框架可分为:集中式和联邦式,其中联邦式方法更为常用[31, 51]。
2.2 观测域信息融合
大量相关研究都致力于将加速度计阵列作为MEMS阵列的信息融合的基础,也有不少算法可以应用于观测域MEMS阵列信息融合。例如,无陀螺仪IMU模型可以采用如下算法进行信息融合算法。让Ωa表示Ωab=a×b的3个元素向量a的斜对称矩阵。将方程(1)写为

(4)
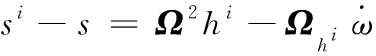
(5)
将每个测量定义为yi为噪声ni,测量方程可以写成N个三元方程:
Y=XR+N
(6)
其中对矩阵的定义为

(7)
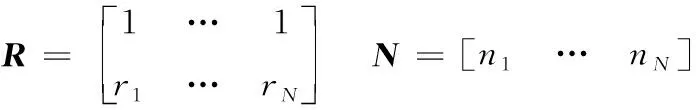
(8)
X的最小二乘估计为
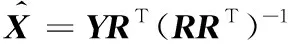
(9)
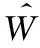

(10)

(11)
但角速度的正负存在符号模糊,即ω×ω=(-ω)×(-ω)。为了解决这个问题可以在GF-IMU中加入陀螺仪[52]。也就是将加速度计提供的角速度与陀螺仪的角速度进行融合。
2.3 估计域信息融合
估计域融合一般基于卡尔曼滤波或其他相关滤波器如扩展卡尔曼滤波,容积卡尔曼滤波等构成,可用于INS/GNSS组合导航信息融合[53]。估计域融合通过一个“主滤波器”将多个IMU的输出数据进行融合,通常是将不同局部滤波器融合成一个组合滤波器。本文中基于集中式架构进行介绍,集中式架构通常由“块”或“堆叠”滤波器组成,在单个块对角线结构中计算单个不相关的状态估计:
δxk+1=Φk,k+1δxk+ωk
(12)
δzk+1=Hk,k+1δxk+ηk
(13)
其中

(14)

(15)

(16)

(17)

3 行人导航修正算法
零速探测器的最佳参数调整依赖于对行人步态的分析,例如用户的步态速度。而如何正确设计一个鲁棒的零速探测器仍然是一个有待解决的研究问题[54]。零速修正中常用的滤波算法为卡尔曼滤波,但卡尔曼滤波只能处理部分线性问题。为此,Foxlin采用扩展卡尔曼滤波器作为ZUPT算法的融合滤波器。此外,零速检测还可以借助惯性传感器之外的传感器。目前,标准的足装惯性导航系统包括:① 惯性导航方程,用于积分惯性传感器测量值,从而提供位置、速度和方向信息。② ZUPT,用于纠正这些位置、速度和方向估计,从而减少误差漂移。③ 零速度探测器,用于检测零速时刻。
3.1 状态-空间模型的公式化
结合惯性导航方程f(·)和零速检测函数h(·),零速的伪测量值yk0,以及零速探测器D0,k→{0,1}可以建立起零速测量模型。零速测量模型仅适用于零速探测器取值为1的采样样本,即当传感器单元是静止时,可采用如下模型表示[24]:
xk+1=f(xk,uk)+wk
(18)
yk=h(xk)+ek∀kDθ,k=1
(19)
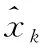
3.2 零速检测器
零速检测器Dθ,k能否准确检测到零速区间,直接关系到整个修正算法正确性,常用的零速检测探测器有[59]:


(20)


(21)
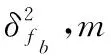
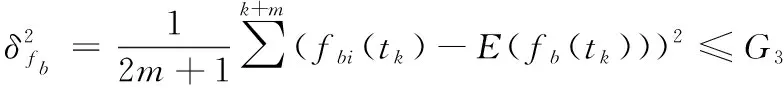
(22)

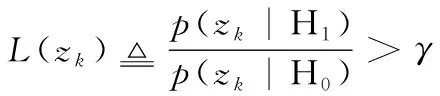
(23)
式(23)中,γ表示指定的阈值。广义似然比检验在零速检测上的应用也促进了姿态假设最优检测器的使用,该检测器使用加速度计、陀螺仪等多种惯性传感器信息进行零速探测,比只使用一种传感器信息的探测器具有更高的准确率[64]。因此通过使用多种传感器测量信息进行互补,可以有效提高零速检测准确率。
4 结论
基于惯性传感器阵列的行人导航系统,通过运用不同的惯性传感器阵列与建模,不同的阵列融合框架与融合算法,能够实现抑制传感器随机误差,提高测量精度的目的。当前传感器阵列的研究趋向于将陀螺仪与加速度计共同组成的阵列结构。引入陀螺仪可以提高加速度计阵列估计角速度的精度,陀螺仪阵列可以有效抑止陀螺仪的随机漂移。由于构成阵列的MEMS为同型号的传感器,它们的传感器误差具有相关性,采用观测域的融合框架更加适合于阵列的融合。结合行人步态的特征,运用零速修正算法,能够抑止行人导航中产生的累积误差,而选取合适的阈值则是零速修正算法精度的关键。
惯性传感器阵列未来的发展趋势:
1) 结合自适应算法,用于状态估计、故障检测和不确定性评估,可以将惯性传感器阵列推广到无人机,机器人等领域。
2) 探索新的误差建模方式与融合算法。
3) 开发自动在线阵列校准工具,实现包括不同传感器信号的时间同步。
4) 探索与其他具有不同动态范围、带宽、误差稳定性特性和采样频率的传感器数据融合方法。这些是惯性传感器阵列领域的研究人员当前和未来的挑战,也是利用新惯性传感器硬件和系统带来的新机遇的先决条件。

