基于最小二乘法的对称分数延迟滤波器设计

邹 正,胡 进,陈 宇

(中国船舶集团有限公司第八研究院,南京 211153)

0 引 言

可变分数延迟(Variable Fractional Delay,VFD)滤波器在数字信号处理中应用广泛,例如任意采样率转换、分数阶微分器设计、数字波束形成[1]等。现有的 VFD有限脉冲响应(Finite Impulse Response,FIR)滤波器算法可分为2类:时域插值算法和频域优化算法,其中前者基于多项式插值,如 Lagrange、Hermite[2-3]等,计算简单,但其高频响应较差;后者因在大带宽下仍能保持良好的幅频响应而受到青睐,常用的优化准则包括最大平坦(MF)[4]、加权最小二乘(WLS)[5-6]和极大极小准则(MM)[7]等。这些分数延迟滤波器存在的主要问题是应用过程中对于硬件资源的消耗巨大。

本文提出一种基于最小二乘法的对称分数延迟滤波器设计方法,可以大幅减少资源消耗,进而降低硬件实现难度。

1 系数对称

首先推导FIR VFD滤波器存在的系数对称性性质,然后利用系数对称性开发一种新的WLS方法来设计VFD FIR滤波器。与现有的WLS方法相比,所提出的基于加权最小二乘法的对称性方法只需要滤波器总阶数的一半抽头系数参与运算即可完成滤波功能。

设计VFD 滤波器的目的是找到一个可变的传输函数H(z,p),使其在指定的通带区域内尽可能准确地接近所需的可变频率响应[8],即

Hd(ω,p)=e-jωp

(1)

式中:ω∈[0,απ]为归一化角频率,0<α≤1是指定通带的一个具体数值系数;p∈[-0.5,0.5]为所需的可变分数延迟。

为了通过有限冲击响应实现Hd(w,p),假设VFD FIR滤波器的传递函数为[9]

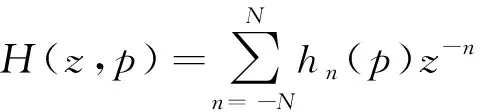
(2)

将系数hn(p)表示为参数p的多项式:

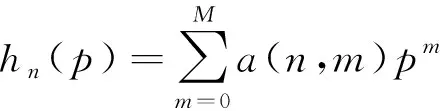
(3)

代入式(2),得到可变传递函数:

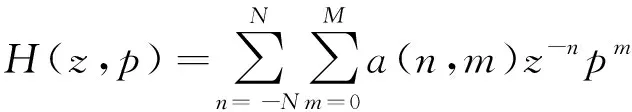
(4)

其可变频率响应为

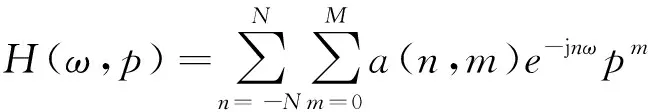
(5)

目标是找到最佳系数a(n,m),使可变频率响应的加权平方误差最小。

(6)

式中:W(ω,p)为一个非负的加权函数;e(ω,p)为实际可变频率响应与期望可变频率响应之间的复值误差,且

e(ω,p)=H(ω,p)-Hd(ω,p)

(7)

在公式处理WLS设计问题之前,推导出式(4)中存在的有用的系数对称性,如式(8)～(13)所示。

式(5)可以进一步改写为

对上式中下划线部分的索引进行置换n′=-n,可得

由于期望的可变频率响应即式(1)满足

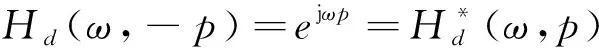
(9)

其中[·]*表示[·]的复数共轭。

则最优H(ω,p)也应该满足

H(ω,-p)=H*(ω,p)

(10)

如果式(6)中的加权函数W(ω,p)对于p来说是对称的,则

将上述划线部分等价,可以得到

a(-n,m)=(-1)ma(n,m)

(12)

而式(12)对于n=0也是成立的,即

a(0,m)=(-1)m·a(0,m)

因此,如果n≠0,

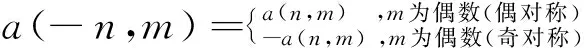
(13)

如果n=0,则a(0,m)=0,m为奇数。

为求得满足需求的VFD滤波器系数,将式(13)的对称系数代入式(8)中,可以得到

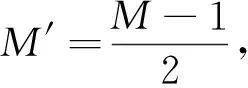
c=[1 cos(ω) cos(2ω) … cos(Nω)]t

s=[sin(ω) sin(2ω) … sin(Nω)]t

Pe=[1p2p4…pM-1]t

Po=[pp3p5…pM]t

(15)

式中:下标e、o分别代表偶数和奇数。

式(14)可以表示成矩阵形式:

H(ω,p)=ctBePe-jstBoPo

(16)

频率响应误差式(7)为

只须找到最佳的系数矩阵Be,就能找到最佳的滤波器系数a(n,m),而Bo则是通过最小化误差函数来实现:

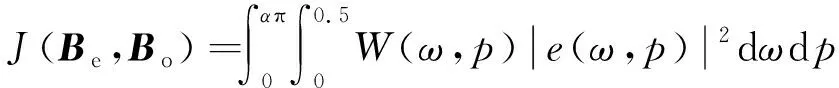
(18)

其中只有区间p∈[0,0.5]需要进行积分。

2 闭合形式的误差函数

本节详细推导闭式误差函数。首先,在式(18)中展开|e(ω,p)|2。由式(17)可得

其中:

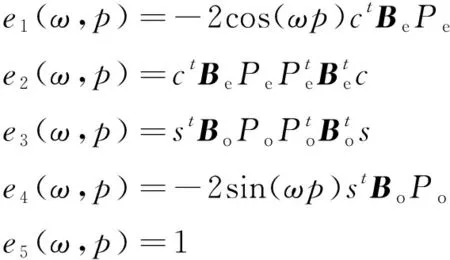
(20)

将式(19)代入式(18),得到

其中:

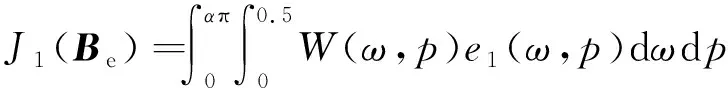
(22)

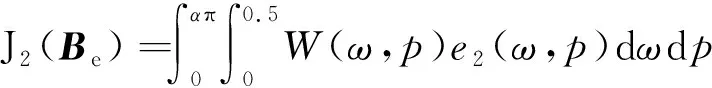
(23)

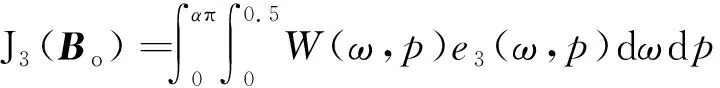
(24)

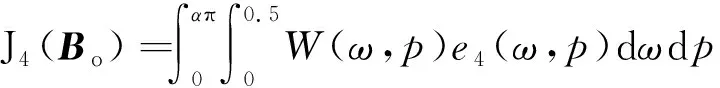
(25)

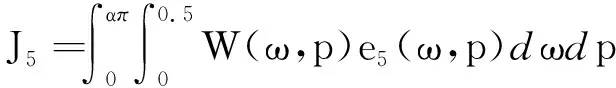
(26)

为了得到闭合形式的J(Be,Bo),假设加权函数W(ω,p)是可分离的,即

W(ω,p)=W1(ω)W2(p)

(27)

此外,W1(ω)和W2(p)分别被假定为ω、p的分段常数函数。将式(20)分别代入式(22)～(26),得到闭式误差函数:

J5=constant

(28)

其中:

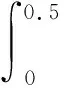
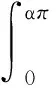
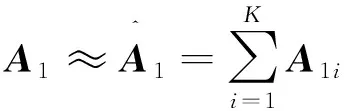
(29)

而且

矩阵A6可以近似为

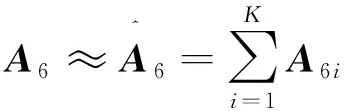
(30)

而且

因此,可以由闭合形式的误差函数式(21)得到

3 最优解决方案

为了得到最佳系数矩阵Be和Bo使式(31)最小化,必须对J(Be,Bo)求对于Be和Bo的微分,然后将微分设为零,即

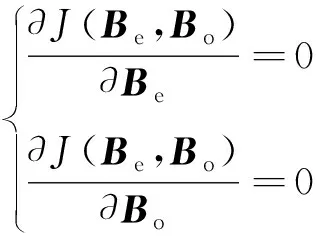
(32)

矩阵A2、A3、A4和A5是对称的,可以得到

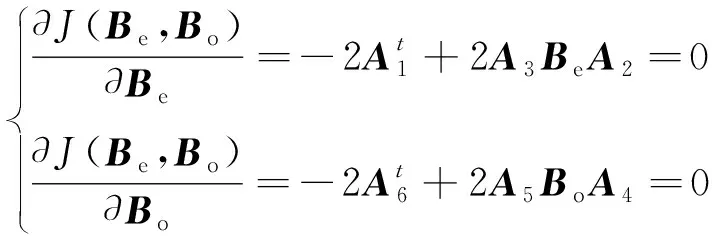
(33)

因此可以通过下式确定最佳系数矩阵:

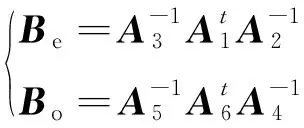
(34)

4 设计实例

理想的可变频率响应为Hd(ω,p)=e-jωp,通过使用变量传递函数式(4),令α=0.9计算出近似可变频率响应的结果。在近似计算过程中假设N=34,M=7,K=10,ω∈[0,απ],以απ/200的步长均匀采样,且分数延迟范围p∈[-0.5,0.5],可以通过以下几个参数评估VFD滤波器的设计精度。可变频率响应的幅度最大绝对误差和最大群延迟偏差(单位dB)分别为

εMax=max{20log10|e(ω,p)|,ω∈[0,απ],p∈[-0.5,0.5]}

εpMax=max{|τ(ω,p)-p|,ω∈[0,απ],p∈[-0.5,0.5]}

其中:τ(ω,p)为实际群延,是频率ω和理想群延p的函数。

图1给出了VFD滤波器在不同频率和延迟值下的幅度误差,其中x轴(p∈[-0.5,0.5])为延迟值,单位为采样周期;y轴(ω∈[0,απ])为归一化的频率值;z轴为可变频率响应幅度误差绝对值,最大为-107.5 dB。图2为图1中粗线标识的最大值的二维平面。

图1 可变频率响应的幅度误差

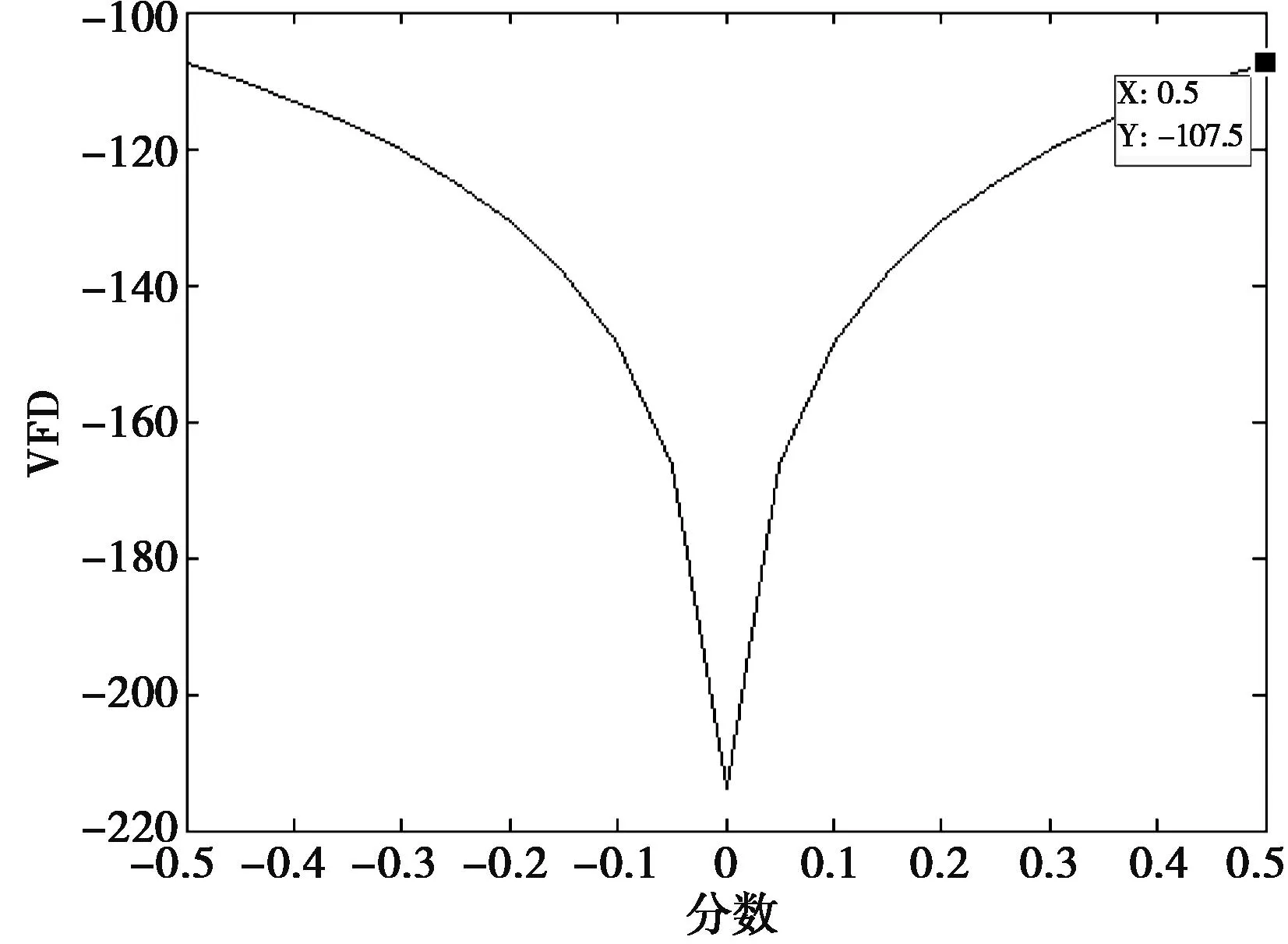
图2 可变频率响应的幅度误差值

实际VFD的延迟值如图3所示。群延迟误差如图4所示,坐标值同图1,表明已经获得了非常平坦的连续可变VFD响应,其最大误差为0.000 377 3。图5为图4中粗线标识的最大值的二维平面。表1为可变频率响应的幅度最大绝对误差和最大群延迟偏差的坐标。

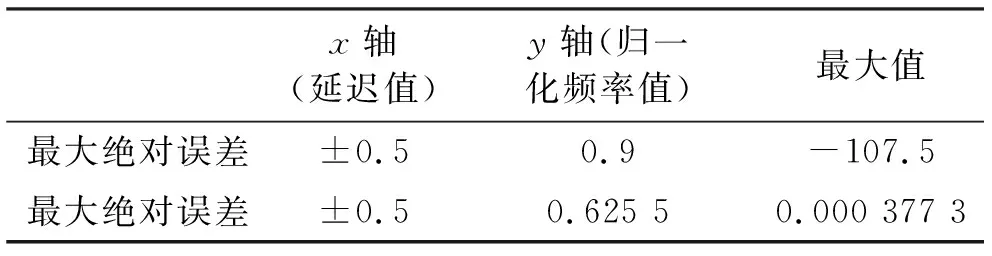
表1 幅度最大绝对误差和最大绝对误差统计表

图3 VFD延迟值

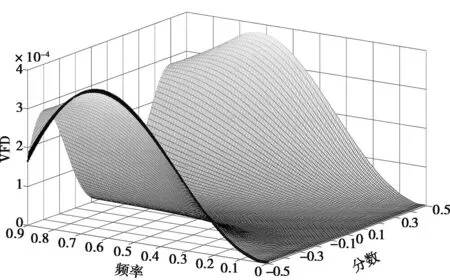
图4 VFD群延迟误差

图5 VFD群延迟误差最大值

5 结束语

利用滤波器的系数对称性可有效设计VFD FIR滤波器。与现有的非对称系数WLS方法相比,本文提出的基于对称性新型WLS滤波器设计方法只需要VFD滤波器系数50%的存储量和乘法器运算资源,因此可以显著降低计算和存储资源,并降低滤波器的硬件成本。同时,在推导闭合形式的误差函数时,由于使用了Taylor级数,可以完全去除数值积分,加快了设计过程,并保证最终系数解的最优性。