不锈钢管悬伸长度对车削颤振稳定性影响分析*
李和伟,梁 利,孙兴伟,杨赫然
(1.沈阳工业大学 机械工程学院,辽宁 沈阳 110870;2.辽宁省复杂曲面数控制造技术重点实验室,辽宁 沈阳 110870;3.沈阳工业大学 软件学院,辽宁 沈阳 110870)
0 引言
细长不锈钢管由于其质量轻、结构紧凑等特点,广泛应用在航空、军事等高精密领域,但细长结构件均存在长径比大、刚性差的问题,在不锈钢管切断过程中,造成切削系统颤振,降低了不锈钢管的切割断面质量[1]。在车削加工过程中,切削颤振是影响车削系统稳定性的重要因素,而切削厚度发生变化会导致再生型颤振[2]。Chen等[3]根据细长结构件的特性,利用欧拉伯努利梁建立振动模型,分析了工件切削颤振的影响因素,并求解了工件在不同装夹条件下切削加工稳定性极限的数值解。Petrakov等[4]使用奈奎斯特图在时域和频域中模拟切削过程,开发了一种预测车削颤振的新技术。鲁燕等[5]揭示了工件长径比和切削三要素对振动响应的影响规律。邵明辉等[6]研究了在不同车削参数下的车削振动情况。
本文基于车削再生理论,研究316L细长不锈钢管悬伸长度对车削稳定性的影响,绘制车削颤振稳定性叶瓣图,结合时域仿真法,验证稳定性叶瓣图预测的准确性。
1 细长不锈钢管车削动力学分析
1.1 细长不锈钢管车削动力学模型
细长管的轴向长度远大于其径向尺寸,因此细长管的刚度远小于刀具系统刚度。假定刀具系统刚度足够,建立的工件切断加工再生型颤振系统动力学模型如图1所示。
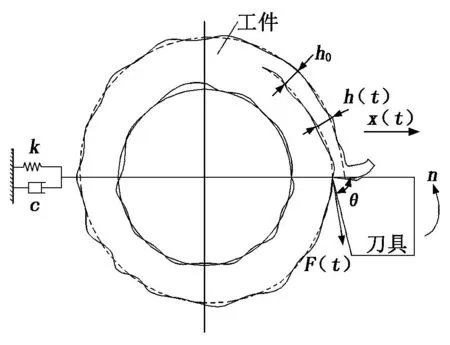
图1 工件切断加工再生型颤振系统动力学模型
图1中,k为工件等效刚度,N/mm;c为等效阻尼,N·s/mm;n为刀具转速,r/min;h0为理论切削厚度,mm;h(t)为动态切削厚度,mm;x(t)为工件振动位移,mm;F(t)为动态切削力,N;θ为切削角度。
(1)
其中:m为工件的等效质量,kg。
动态切削力F(t)可表示为:
F(t)=kfbh(t).
(2)
其中:kf为切削刚度系数,N/mm2;b为切削宽度,mm。
工件上一转的振动位移与本次的振动位移存在差值,切削厚度h(t)将随时间不断发生变化,进而影响切削力F(t)的变化,不断变化的切削厚度h(t)可表示为:
h(t)=h0-[x(t)-x(t-T)].
(3)
其中:h0为理论切削厚度,mm;T为刀具绕工件旋转一周的时间,s。
联立以上公式并整理,可得系统切削颤振方程为:
(4)
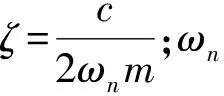
1.2 车削过程的稳定性预测分析
对式(3)、式(4)进行拉普拉斯变换可得:
h(s)=h0+(e-sT-1)x(s).
(5)
x(s)=Φ(s)F(s)=Φ(s)·kfbh(s).
(6)
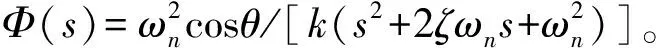
结合式(5)与式(6),可得切削厚度系统的闭环传递函数:
(7)
式(7)中,分母为闭环传递函数的特征方程,传递函数的稳定性取决于其特征方程的根s=σ+jω,由Nyquist稳定判据可知,当特征根s的实部σ=0时,切削颤振系统处于临界稳定状态。将特征根s=jω代入特征方程,并结合欧拉公式整理可得:
(8)
其中:λ=ω/ωn,ω为切削振动系统的颤振频率。
将刀具转速n=60/T代入式(8),并解该方程组,整理可得刀具转速n及极限切削宽度blim的表达式为:
(9)
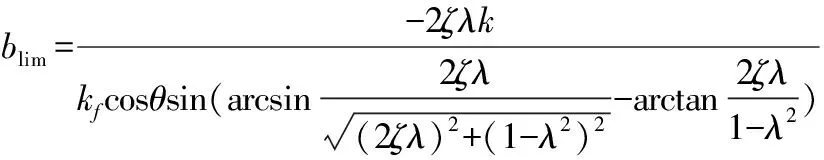
(10)
式(9)中,i=1,2,3,…。根据式(9)和式(10)即可绘制出车削系统稳定性叶瓣图,预测切削系统的稳定性。
2 车削颤振系统稳定性极限分析
2.1 车削颤振系统稳定性极限预测
在细长不锈钢管的车削动力学参数中,切削刚度系数kf=350 N/mm,阻尼比ζ=0.015,切削角度θ=80°,设置工件的模态参数如表1所示。
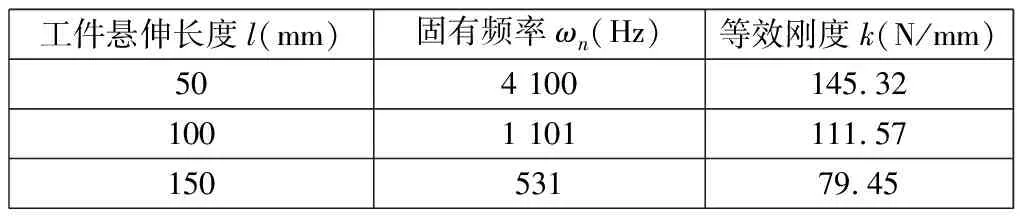
表1 工件的模态参数
将车削动力学参数代入式(9)、式(10),利用MATLAB编写程序绘制的叶瓣图如图2所示。由图2可见,随着悬伸长度l增大,稳定性极限切削宽度值blim减小。
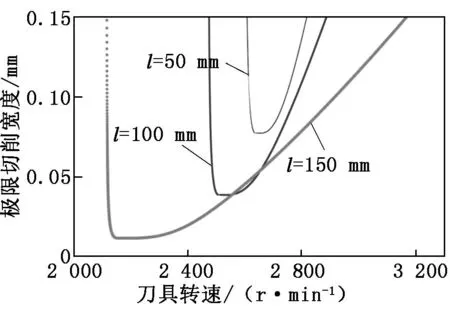
图2 随工件悬伸长度变化的车削系统稳定性叶瓣图
2.2 车削颤振时域仿真
利用MATLAB中的Simulink模块搭建车削时域仿真平台,如图3所示。
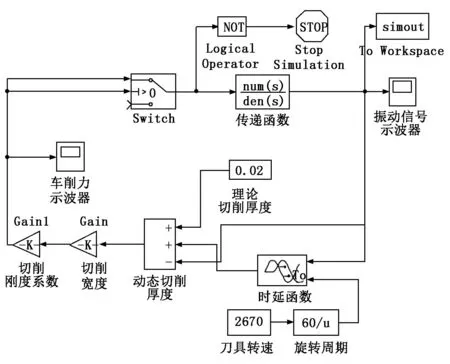
图3 车削时域仿真平台的搭建
结合切削颤振稳定性叶瓣图,在刀具转速为2 670 r/min时,选取切削宽度在0.05 mm~0.08 mm之间的6点基于搭建的仿真平台进行分析,得到工件不同悬伸长度下的时域仿真结果,如表2所示。
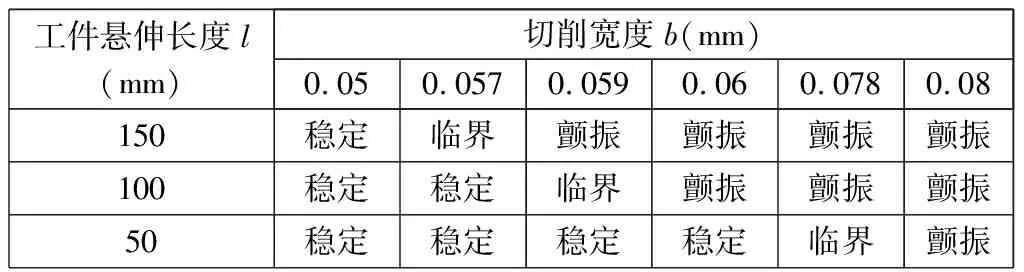
表2 工件不同悬伸长度的时域仿真结果
以表2的切削宽度数值作为时域仿真的输入,得到悬伸长度为150 mm时随时间变化的振动信号,如图4所示。由图4可知:当切削宽度在切削颤振稳定性叶瓣图耳垂线以下的区域时,振动信号经衰减后变得收敛,趋于平衡状态;当切削宽度在切削颤振稳定性叶瓣图耳垂线处的区域时,振动信号以较小的幅值发生振动,系统处于临界稳定状态;当切削宽度在切削颤振稳定性叶瓣图耳垂线以上的区域时,振动信号发散,系统产生振动。通过时域仿真与稳定性叶瓣图预测曲线对比,验证了细长管车削颤振稳定性预测模型的可靠性。
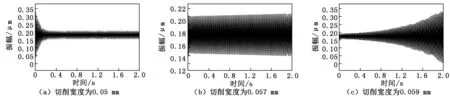
图4 悬伸长度为150 mm、不同切削宽度时的振动信号
由表2可以发现:当工件悬伸长度越长时,系统稳定对应的切削宽度越小,越容易发生振动。将切削宽度为0.08 mm、3种悬伸长度分别输入时域仿真平台中,得出切削宽度为0.08 mm的振动信号,如图5所示。由图5可知:在同一切削宽度条件下,工件悬伸长度越长,其振动信号的幅度变化越大,可见工件悬伸长度越大的切削系统稳定性越差。
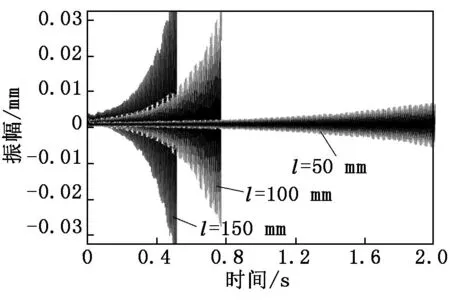
图5 切削宽度为0.08 mm、不同悬伸长度时的振动信号
3 结论
针对细长不锈钢管的结构特点,建立切削颤振系统的数学模型,在此基础上,通过编写程序绘制切削颤振系统稳定性叶瓣图,预测切削工艺参数对切削系统稳定性的影响。搭建时域仿真平台进一步分析工件不同悬伸长度对切削系统稳定性的影响,并验证切削颤振系统稳定性叶瓣图的可靠性。采用时域仿真方法,结合稳定性叶瓣图可知,细长不锈钢管在加工过程的悬伸长度越短,极限切削宽度值越大,越有利于切削系统平稳加工。本文研究可为细长不锈钢管切削工艺参数的选取提供理论指导。

