大型多组分天然气管网系统稳态组分分布模型

薛向东，宋永红，张 博，朱 峰，阎 涛

1.西安交通大学软件学院，陕西西安 710049

2.国家管网集团科学技术研究总院分公司，河北廊坊 065000

3.国家管网集团建设项目管理公司，河北廊坊 065000

天然气管网系统的稳态组分占比计算是指，在稳态工况下，以水力仿真所得气体体积流量与流向参数为基础，通过稳态组分跟踪模型求解管网内各节点与任意管道处的每种组分的占比。天然气管网的组分跟踪在管网调控中具有重要意义。多气源混输管网是未来天然气管网的发展趋势之一[1-2]，由于不同气源的气体组成不同，这意味着管网内将发生频繁的组分掺混，管网中组分占比也难以确定。由于天然气中组分的变化会导致气体热值的变化，因此需要进行组分占比计算以确保用户用气质量的稳定。此外，某些组分如H2与H2S等会对管道造成氢脆或腐蚀等危害[3-4]，同样需要计算这些组分在管网中所有管道内的占比以确保管道安全。因此，天然气管网稳态组分占比计算对于管网调控具有重要意义。

目前，国际上关于多气源管网的组分与热值占比仿真已经取得一些成果。2001 年，德国在PSIG 年会上报告了一种在VNG-Verbundnetz 天然气股份公司和天然气进口商中应用的管道热值模拟方案，作为管道热力计费的依据[5]。FLUENT 也可以实现对多气源混输管网的组分分布的稳态仿真[6]。除此之外，还有一些国外学者进行了多气源混输管网组分分布的研究。比如，Pellegrino[7]研究了稳态工况下向天然气管网中混输绿色燃料（比如氢气或生物甲烷等）的管网仿真模型；该模型的一个特点是定义了一个名为“伪电导”的参数，将管道内流体流动的动力学问题用电流来模拟；但是，该方法需要分别对管道、压气站、调压站建模，因此模型较为复杂。同时，该模型在求解时需要不断迭代各节点压力、温度与各节点组分，当初始值选取不当时极易出现不收敛的情况，因此数值稳定性差。Cavana[8]等采用Pellegrino 提出的框架研究了稳态工况下小型燃气管网中混输生物甲烷的气体质量跟踪方法；与Pellegrino 相比，其简化了非管道元件的建模，但是，求解流程并没有做出简化，依旧需要依次迭代管网内压力、组分与温度参数并最终达到平衡。Abeysekera[9]通过两个步骤完成分布式注入燃气管网的稳态模拟，即首先建立一个名为“节点流分析顺序”的算法模块用以存储管网中各节点的分支数量与流向，并对每个分支编号；在计算程序处，调用“节点流分析顺序”模块进行气体组分计算、热值计算、气源占比计算与压力分布计算，并最终输出结果；这种方法可以保证对复杂管网连接信息的提取，因此适用于复杂管网的计算，但存储空间较大。Chaczykowski 等[10-12]研究了不同气质、气源天然气注入管网时气体的组分跟踪方法，可以跟踪管道出口热值、某些气体组分（如C2H6、CO2等）的变化。该方法可以用于管网瞬态组分仿真，但是对于大型管网来说，仍需要一种可以精确、简便、快速的求解方法。相比之下，国内管网仿真软件对于气体成分、热值仿真与气源跟踪领域存在不足。在稳态管网组分仿真模型研究方面，童睿康[13]在传统天然气管网水力、热力模型的基础上，通过补充稳态工况下气体组分方程、热值方程与气源比例方程构建了多气源混输天然气管网的数学模型，并采用节点-节点法来创建管网结构数组，从而描述管网的拓扑结构；然而，通过这种方法构建的管网组分分布计算模型逻辑上较为复杂，且对于大型复杂管网来说计算时间长，效率不高。

本文提出了一种稳态天然气管网组分占比计算模型，该模型基于管网节点掺混方程与管道组分约束方程，对管网整体建立求解矩阵，并采用直接LU 分解的方法进行求解。采用此方法建立的模型不仅可以求解任意结构管网的组分占比，且由于是对管网整体进行直接求解，因此在应用于大型复杂管网时具有模型简明、计算效率高、求解速度快的特点。采用国外某商业软件进行检验，验证了模型的准确性。模型可以用于大型稳态天然气管网的组分占比计算。

1 稳态组分分布计算模型

1.1 基本假设

对于稳态工况，管网中所有流体处于平衡状态。同时，可以将管网内每条管道中的流体看作一整个含有恒定组分的大批次。因此，对于稳态管网，可以做出3 个基本假设[14-19]：其一，各个气源的组分不随时间发生变化；其二，每条管道内的天然气组分保持一致；其三，管道内的天然气在节点处均匀混合后从节点流出。

1.2 约束方程

在稳态管网组分占比计算模型中，约束方程共有两类：一类是内部节点（除气源点外的管网节点）的组分掺混方程，用于计算管网内部节点的组分分布；另一类是管道元件的组分约束方程，用于计算管道元件中的组分分布。

1.2.1 管道元件组分约束方程

对于稳态模型，可认为管网中每条管道内组分恒定不变，因此对于每条管道只需要一个约束方程来约束其组分。由于管道与节点连接，且流体是连续的，因此认为与节点相连的所有下游管道内的组分分布一致。可以得到元件组分约束方程，针对P个管道元件可以建立P个约束方程：

式中：αP,λ为第P个管道元件中λ组分的摩尔分数，αupP,N(E),λ为第P个管道元件中的上游节点N或上游非管道元件E处λ组分的摩尔分数。

1.2.2 节点掺混方程

对每一个内部节点采用组分完全掺混假设，可以得到组分掺混方程：

式中：αN,λ为节点N中λ组分的摩尔分数；QP为流入管道P的体积流量，m3/s。

1.3 闭合关系

除了管道中的组分约束方程和节点中的掺混方程外，还需要补充边界条件方程和非管道元件的约束方程，以使方程组闭合。一方面，各气源点中各组分的摩尔分数为已知量，该条件可以作为边界条件方程；另一方面，还需要引入第E个非管道元件的约束方程，针对第E个非管道元件可以建立E个约束方程，即：

式中：、分别为第E个非管道元件的上游、下游节点处λ组分的摩尔分数。

1.4 矩阵构建

对于一个管网系统，假设其具有n个节点（其中有s个气源点），e个非管道元件，p个管道元件，则对于组分i，基于管网整体可以联立出s个边界条件方程、（n-s）个内部节点掺混方程、p个管道组分约束方程与e个非管道元件约束方程，并表示为如下矩阵形式：

Q为流量系数矩阵，其阶数为（n+p）×（n+p），Q矩阵组成如下：

式中：Qj,k表示第j行第k列节点的流量。

如果节点m为气源点，则：

如果节点m为非气源点时，假设为非管道元件E的下节点，则：

式中：下标f为以节点m为下节点的非管道元件E的上节点。

如果节点m为非气源点时，假设k管道为节点m的上游管道，则：

式中：qm,k为与m节点相连的k管道中的体积流量，m3/s。

当n+1≤i≤p+n时，Qi,j表示管道的流量矩阵元素，则：

α为待求稀疏矩阵，为一个（n+p）阶列矩阵，其组成为：

式中：αiNn表示节点n中组分i的摩尔分数，αiPp表示管道p中组分i的摩尔分数。

b为（n+p）阶列矩阵，其组成为：

式中：下标m表示矩阵中的列。

当1≤m≤n时，表示的是节点中组分i的b元素值；当n+1≤m≤n+p时，表示的是管道中组分i的b元素值。当1≤m≤n且m为气源点时，若m节点即为气源点j，则等于aij，aij为气源j中组分i的摩尔分数。

1.5 矩阵求解

对于上述管网组分分布矩阵，可以采用直接LU 分解的方法对Q矩阵进行求解，分解求解公式如下：

式中：αij为原矩阵中的元素，这里为流量系数矩阵Q中的元素。因此，可以将原流量系数矩阵分解为：

式中：L和U分别为一个下三角矩阵和一个上三角矩阵，即：

再通过如下步骤进行求解：

式中：y为采用直接LU 分解法求解时的一个中间矩阵。

式（17）与式（18）为矩阵向量表示的形式，因此将其改写为：

式（13）、式（19）与式（20）即为该稳态组分分布计算模型的求解公式。

2 案例研究

2.1 案例分析

以图1 所示的8 节点管网为例。假设该管网的水力工况如表1 所示；假设有节点1 与节点6 两个气源点，其组分构成如表2所示。

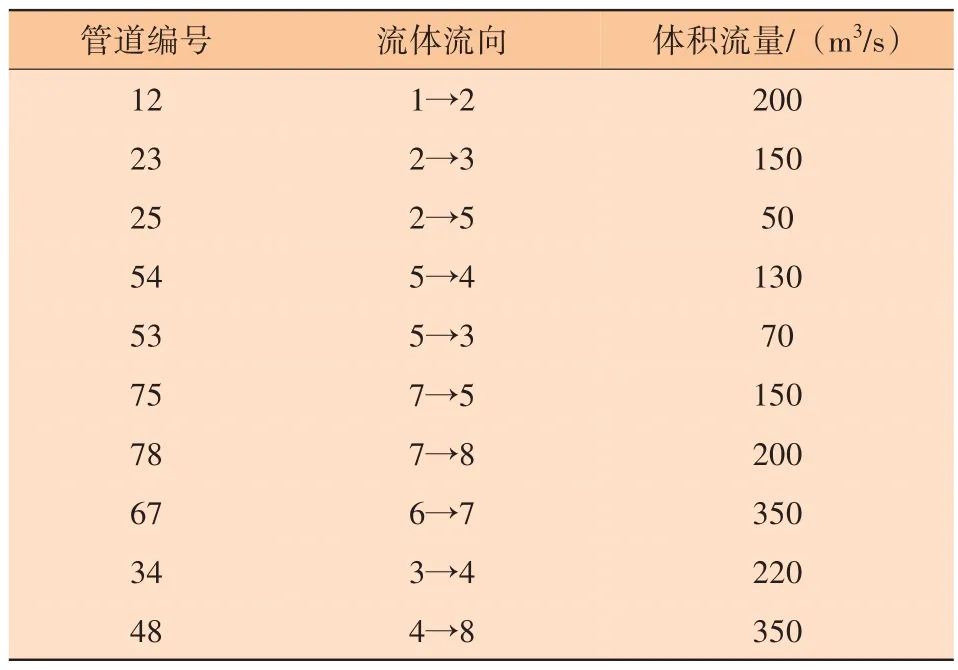
表1 案例管网水力工况

表2 案例管网气源组分构成

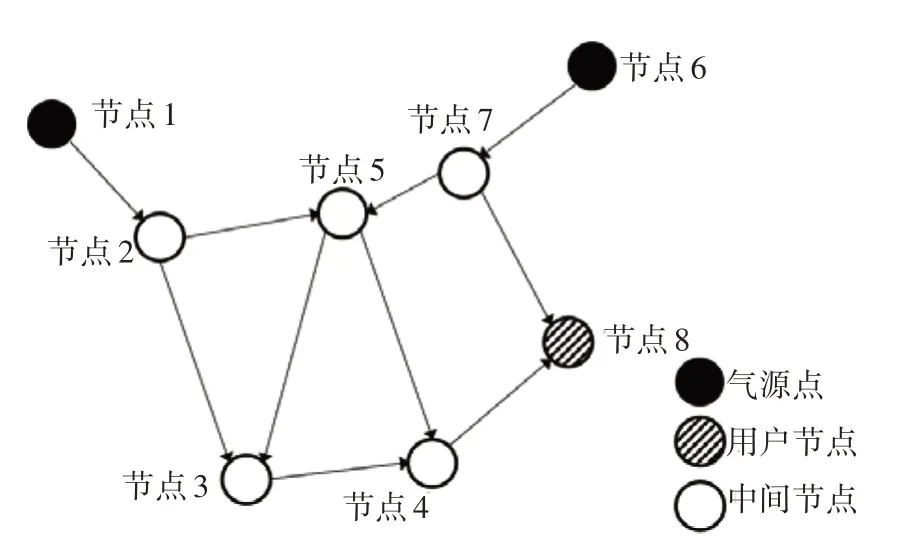
图1 案例管网示意

2.2 模型验证

基于C#语言逻辑，以本文提出的稳态管网组分占比计算模型为理论基础，采用微软公司开发的Visio_Studio 编程软件编写8 节点任意结构管网组分占比计算程序。

采用某商业软件建立模型，分别利用如上8节点任意结构管网组分占比计算程序与某商业软件按照表1 与表2 的工况进行求解，对本文提出的稳态天然气管网组分占比计算模型进行验证，某商业软件模型建立结果如图2 所示。由于节点2 与节点7 分别和气源点1 与气源点6 通过单根管道相连，因此节点2 与气源点1 的组分一致，节点7 与气源点6 的组分一致。因此，在采用某商业软件建立模型的过程中，省略气源点1 与气源点6，将节点2 与节点7 当作气源点进行初始组分参数的设置。

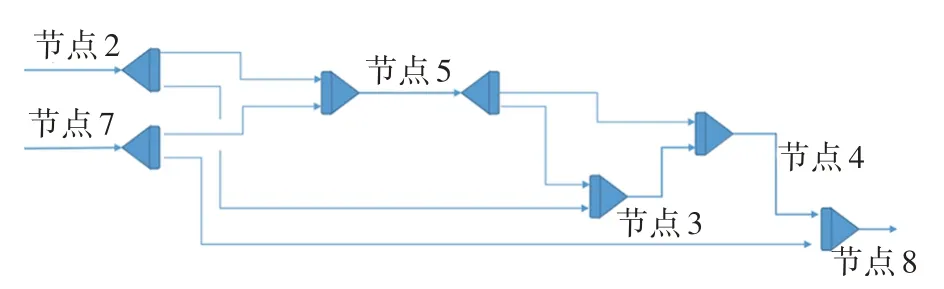
图2 案例管网采用某商业软件建立的模型

除节点1、节点2、节点6、节点7 属于单一输入源的节点，其组分分布与设定组分一致外，其余节点的组分验证结果如表3所示。

表3 组分跟踪模型验证结果

从表3 中可以看出，采用本文提出的稳态天然气管网组分占比计算模型分别计算包括节点3、节点4、节点5、节点8 在内的四个掺混节点的组分分布，与某商业软件模拟的误差均在1%以内。其中，四个掺混节点CH4组分的平均计算误差为0.041%，四个掺混节点C2H6组分的平均计算误差为-0.397%，四个掺混节点C3H8组分的平均计算误差为-0.504%，误差均在可接受范围内，故此认为本文提出的模型具有可行性。

2.3 结果分析

基于本文提出的稳态管网组分占比计算模型，采用8节点任意结构管网组分占比计算程序对案例管网进行求解，得到天然气管网稳态工况下各节点与管道中的组分占比（摩尔分数），求解结果如表4所示。

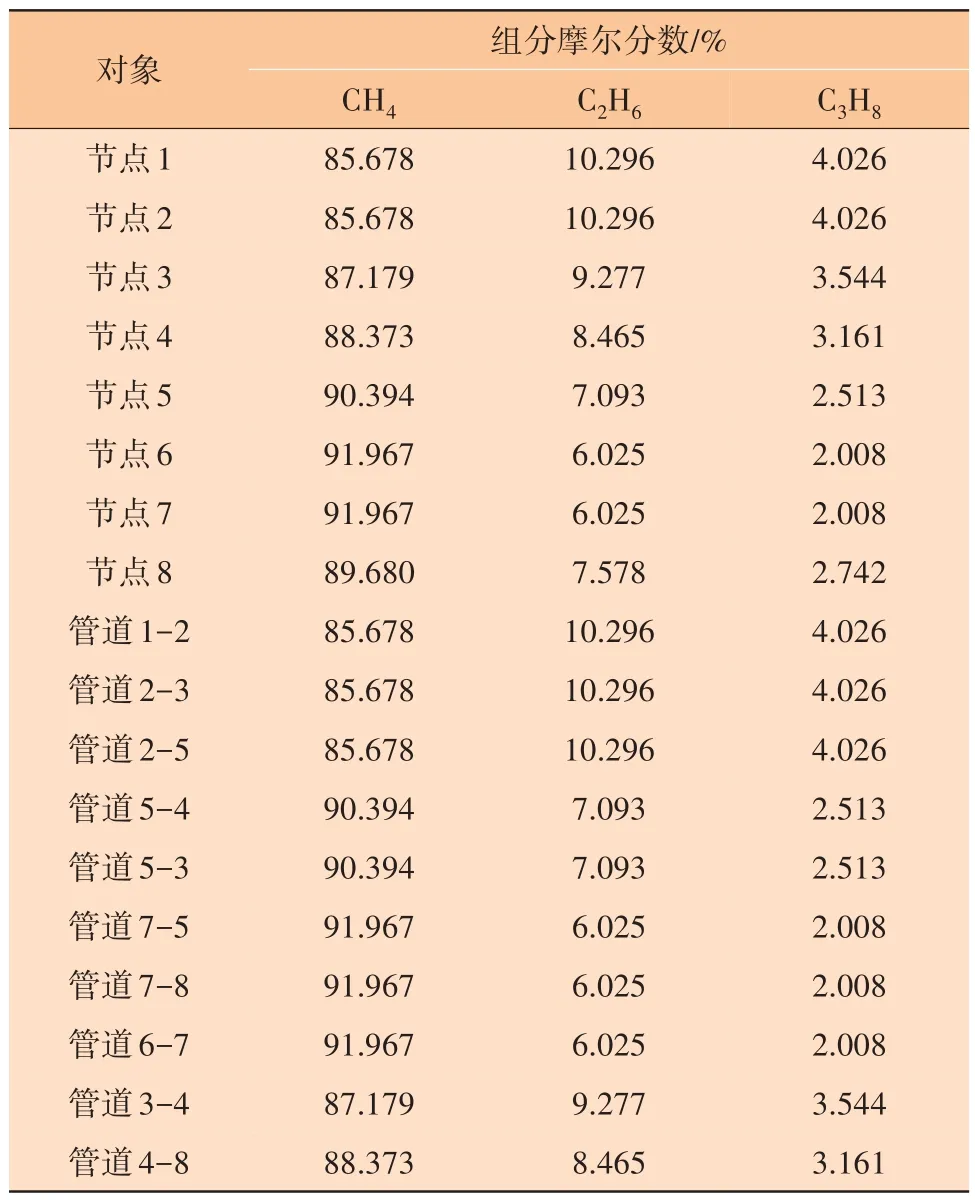
表4 组分占比模拟结果

从表4 可以看出，除气源点外，节点5 的甲烷占比最高，节点8 与节点4 中的甲烷占比次之。这是因为节点5 中气源6 的比例最高，而节点8 与节点4 的气源6 占比次之，而在案例工况中气源6 的甲烷组分浓度高于气源1中的甲烷组分浓度，因此当内部节点的气源占比构成中气源点6的占比较高时，其甲烷组分的浓度就较高。

从表4 还可以看出，管道3-4 的组分构成与节点3一致；管道5-4、管道5-3的组分构成与节点5一致；管道4-8与节点4的组分占比构成一致。

从图1 中可以看出，节点3 是管道3-4 的上游节点；节点5 是管道5-4、管道5-3 的上游节点；节点4 是管道4-8 的上游节点，这符合管道元件的组分约束。

通过如上分析，证明该模型可以正确地表示任意结构管网中的拓扑结构。

3 结论

本文提出了一种天然气管网稳态组分占比计算模型，基于上述模型编写任意结构8节点管网组分占比计算程序，并采用国外某商业软件针对一个管网案例进行模型验证。本文得出以下结论。

1）提出了一种稳态天然气管网组分占比计算模型。模型在基于水力计算结果的基础上，以管网整体为对象，构建管网组分分布矩阵，并采用直接LU 分解的方法进行求解，得到任意结构稳态天然气管网中各节点与管道元件内每种天然气组分的摩尔分数。

2）利用国外某商业软件通过一个管网案例进行了模型验证，模型求解结果与某商业软件求解结果间相对误差均低于0.6%，具有可行性。

3）本文提出的稳态管网组分占比计算模型可以用于任意结构、任意规模的稳态天然气管网组分占比计算。在应用于大规模稳态天然气管网的组分分布计算时，该模型具有求解速度快、泛用性强、逻辑清晰、内存占用低的特点。

建议在后续研究中，进一步开展对瞬态工况下管网组分跟踪模型的研究。