基于空间映射法的微带滤波器设计方法

李平宇,臧 恒,王 康

(中国船舶集团有限公司第八研究院,南京 211153)

0 引 言

为了满足现代雷达系统小型化需求,对微带滤波器进行了折叠缩小,从而引入了更多的参数,若直接利用传统全波电磁仿真工具进行优化,虽然可以得到较好的结果,但是耗费的时间成本和硬件资源很高,无法快速完成滤波器设计。电路仿真软件也可以快速完成仿真,但无法保证设计精度。

John W Bandler等人于1994年提出的空间映射法巧妙融合了电路仿真的快速性和电磁仿真的准确性[1],广泛用于各种滤波器设计。本文提出一种基于空间映射法的微带滤波器快速设计方法,将电路仿真模型作为粗糙模型,全波电磁仿真模型作为精准模型,通过误差函数建立两者参数之间的映射关系,不断迭代优化,在10次全波仿真后得到滤波器尺寸参数,并开展了实物测试验证。

1 基本理论

1.1 四分之一波长短路短截线带通滤波器

四分之一波长短路短截线组成的带通滤波器拓扑图如图1所示[2]。

图1 短路短截线微带滤波器

短截线和连接线长度均为λg0/4,其中λg0对应中心频率f0时的波导波长。对于一个n阶的短截线滤波器,短截线和连接线的特性导纳分别为Yi,i=1,2,…,n和Yi,i+1,i=1,2,…,n,共同决定带通滤波器频率响应。特征导纳可以由以下公式得到[3]:

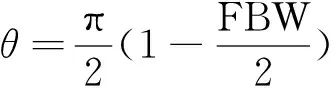
(1)

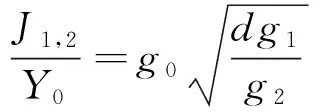
(2)

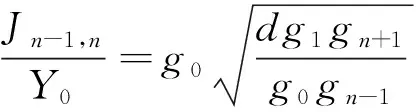
(3)

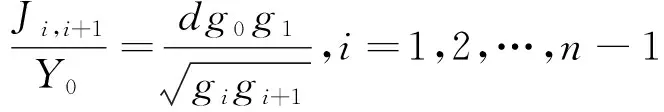
(4)

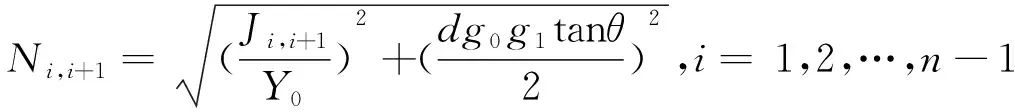
(5)

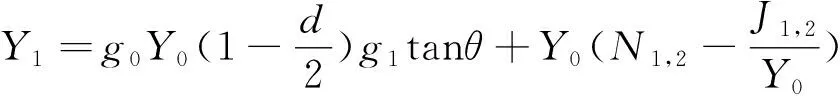
(6)

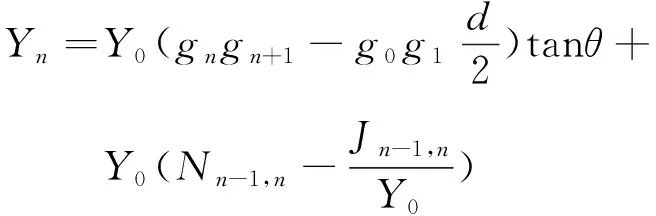
(7)

i=2,3,…,n-1

(8)

(9)

式中:FBW为滤波器的分数带宽;d=2为一个无量纲的常量;gi,i=1,2,…,n为低通原型滤波器的元件值,给定归一化截止频率为Ωc=1。

计算得到各短截线和连接线的特性导纳,再结合介质基板的参数计算出微带线宽度[4],微带线长度为中心频率处波导波长的四分之一。以此作为滤波器初始尺寸,通过仿真软件进行优化,就可以得到较好的S参数性能。

1.2 空间映射法

空间映射法通过建立粗糙模型和精确模型之间的参数映射关系,从而获得合适的替代模型,即校准后的粗糙模型,该替代模型的仿真速度远快于精确模型,且至少拥有粗糙模型的准确性。在具体实施过程中,粗糙模型可以进行快速更新和优化,而只须将优化结果代入精确模型中验证,从而将众多优化工作代入粗糙模型中完成,以最少的精确模型仿真次数来获得满意的优化结果[5]。一个优化问题的数学求解通常可以表示为

(10)

式中:R为随频率变化的电路响应函数;x为一个n阶矢量设计参数;U为目标函数;x*为所要求的最优解,假设解具有唯一性。

将粗糙空间和精确空间的设计参量分别表示为xc、xf,其对应的空间响应结果矢量分别表示为Rc(xc)、Rf(xf)。假设存在矩阵P对应两个模型之间的映射关系,可以得到以下表达式:

xc=P(xf)

(11)

Rc(P(xf))≈Rf(xf)

(12)

将粗糙空间响应向精确模型的响应逼近,求出粗糙空间的设计值,可以表示为

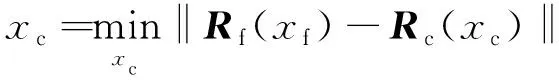
(13)

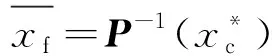
(14)

空间映射法的一种应用方式是通过多个仿真软件进行设计参数提取。例如,使用电路仿真软件AWR作为粗糙空间模型,在AWR中根据具体电路要求设置好优化目标,通过电路仿真快速得到一个初步最佳设计值,将其定为理想值,然后将该设计值代入精确空间模型中进行仿真(如全波电磁仿真软件HFSS),判断结果是否满足要求。如果不满足,则将HFSS得到的S参数导出为S2P文件,在AWR中进行曲线拟合,使得粗糙模型结果逼近精确模型结果,此时对比粗糙模型结果与理想值之间的差距,调整精确模型,多次迭代,使精确模型优化至相应目标。

2 微带滤波器设计

2.1 滤波器结构

利用空间映射法设计滤波器须要建立两个仿真模型,即电路仿真软件AWR中的粗糙模型和全波电磁仿真软件HFSS中的精确模型。本文所设计的四分之一波长短截线滤波器拓扑结构如图2所示,同时也是滤波器的精确模型,该滤波器结构左右对称。所采用的介质基板为Rogers 3003C,基板的相对介电常数εr=3,厚度h=0.254 mm。

图2 滤波器几何结构

该滤波器对应的粗糙模型即电路模型,该模型左右对称,其中连接线采用折叠线以减小电路尺寸,共有10个优化参数,分别对应短截线和连接线的长度、宽度。

2.2 滤波器设计

设定滤波器的中心频率为10 GHz,带宽为4 GHz,通带内反射系数小于-20 dB。首先在AWR中优化滤波器电路模型,得到滤波器电路模型初始最优值响应,此时优化参数值见表1,S参数如图3所示,该优化值下的S参数满足滤波器的设计要求。

表1 电路模型优化参数最优值(单位：mm)

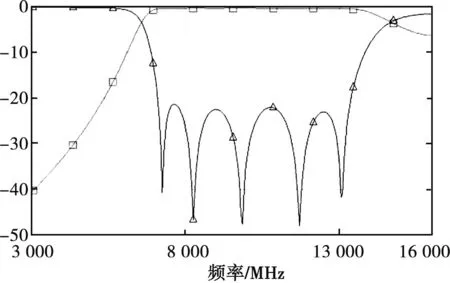
图3 滤波器理想电路模型结果

此时将该优化值作为其初始值传递到精确模型即HFSS中进行建模,基于此建立的HFSS模型往往与电路模型的S参数有所不同。为了修正粗糙模型和精确模型的映射关系,将HFSS模型的S参数导出为S2P文件,再将S2P文件导入AWR软件中,使用电路模型拟合该S参数,优化过程可由图4表示。

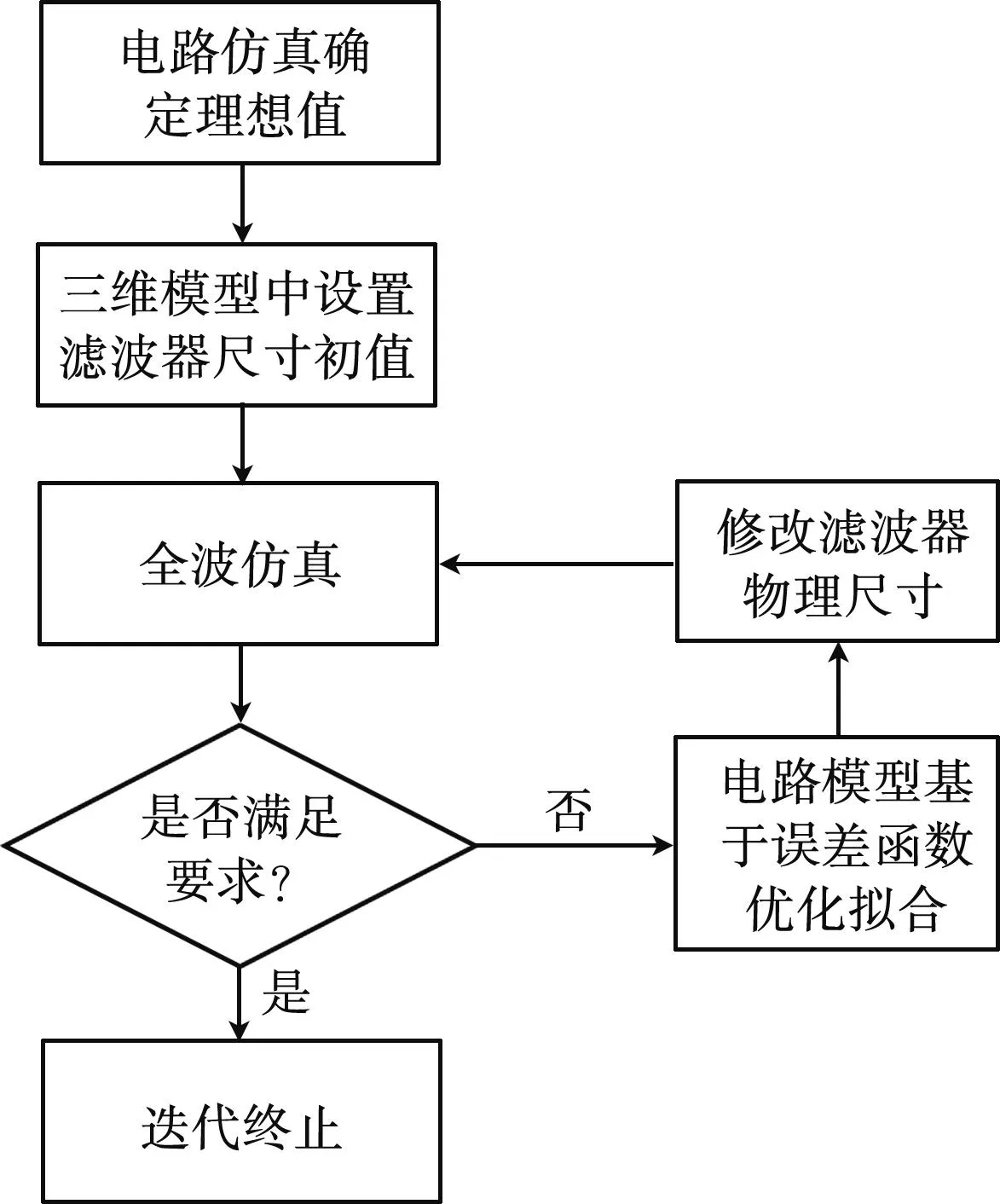
图4 空间映射法优化过程

优化工程中最重要的是误差函数的选取,误差函数用于将粗糙模型的响应向精确模型的响应逼近,好的误差函数可以加快逼近速度,而差的误差函数收敛速度较慢,甚至导致无法收敛。

3 滤波器优化过程

滤波器优化过程快慢取决于误差函数的选取,误差函数用于将电路模型的仿真结果拟合到全波仿真结果,从而实现粗糙模型到精确模型的对应关系。本文将HFSS模型仿真得到的S参数导入回AWR中,通过误差函数使得AWR仿真结果向HFSS结果逼近。在选取误差函数时,由于S21变化较小,所以选取S11作为拟合曲线,而S11曲线极小值位置变化敏感,不适合作为误差函数拟合点,因此误差函数采用分段的方式建立。对于本文的滤波器S11曲线,选取其极大值周围区域作为误差函数分段区间,在AWR中设置误差函数,如图5所示。

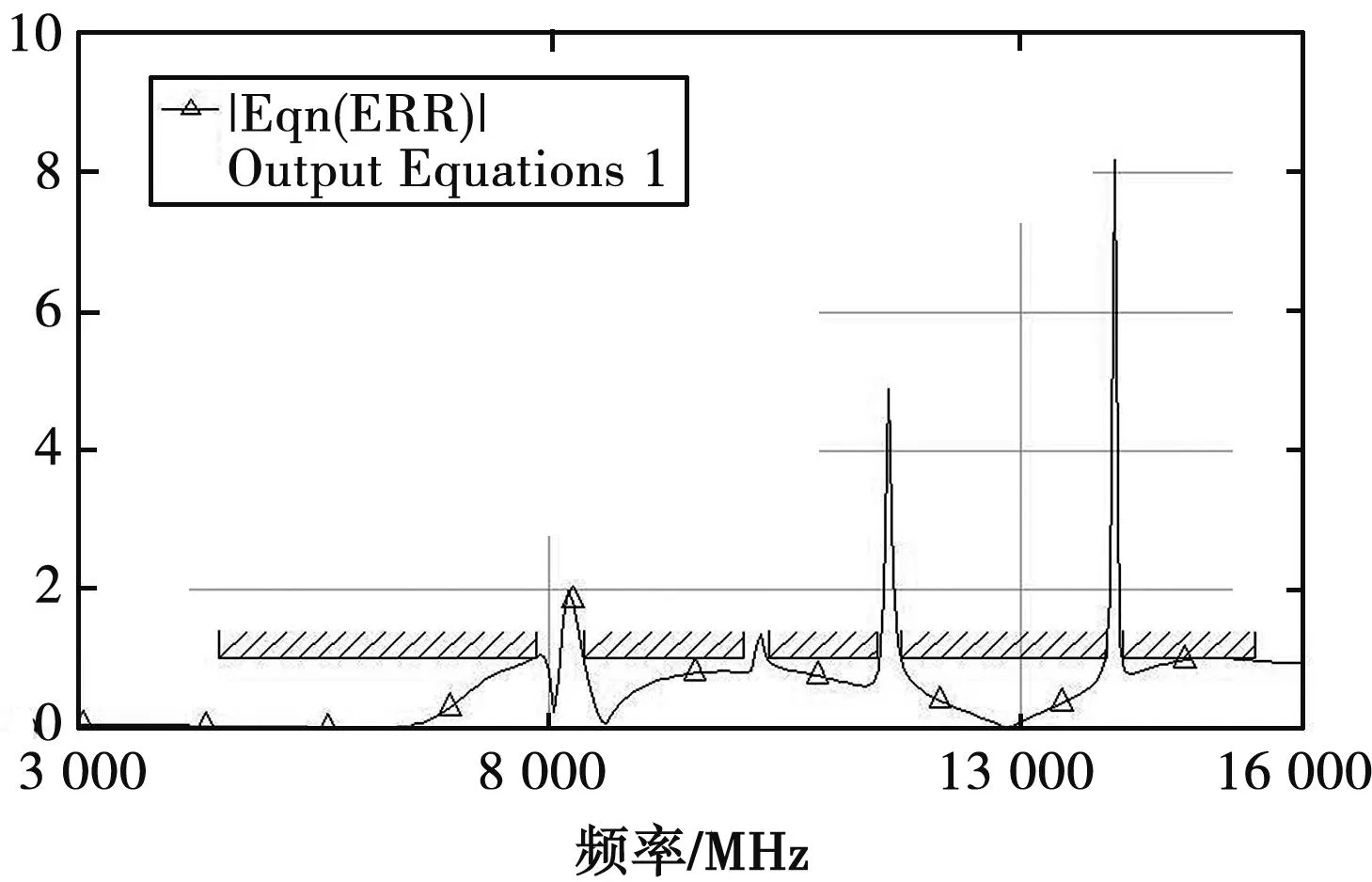
图5 误差函数分段区域

图中拟合曲线已完成收敛,误差较大位置为S参数极小值处,若不分段设置误差函数,该位置将难以收敛,直接影响拟合速度。在拟合完成后,通过对比此时电路模型各参数值与最优值的差距,可以大致判断全波仿真模型各参数值是偏大还是偏小,从而无须进行全波仿真的扫参,也能在多次迭代后得到最优参数。由于本文采用的折叠线参数较多,共进行10次全波仿真,得到满足条件的滤波器物理尺寸,如表2所示。

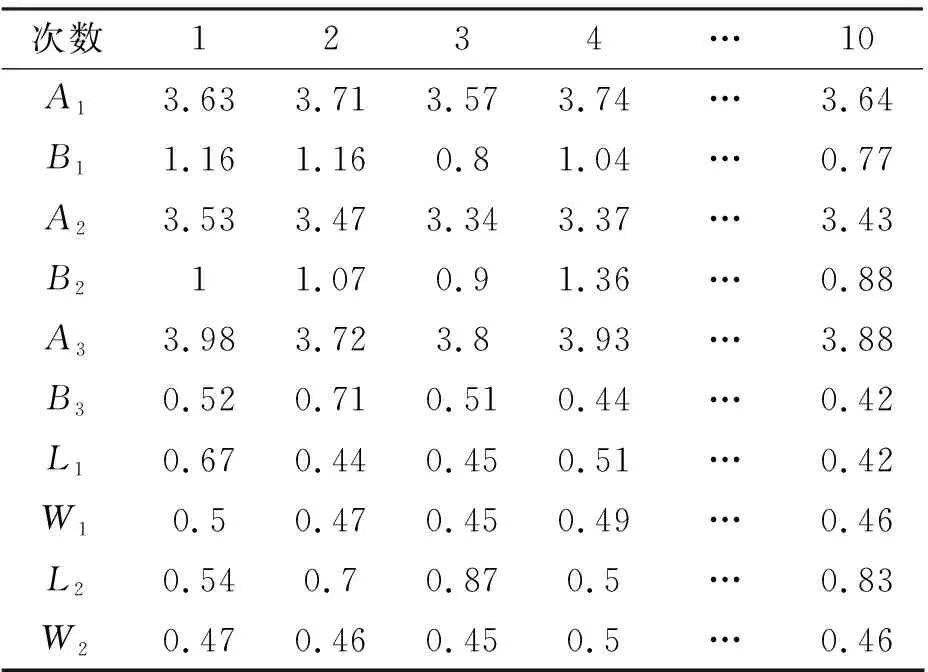
表2 滤波器尺寸优化过程

在第10次全波仿真时得到的S参数满足要求,结果如图6所示。

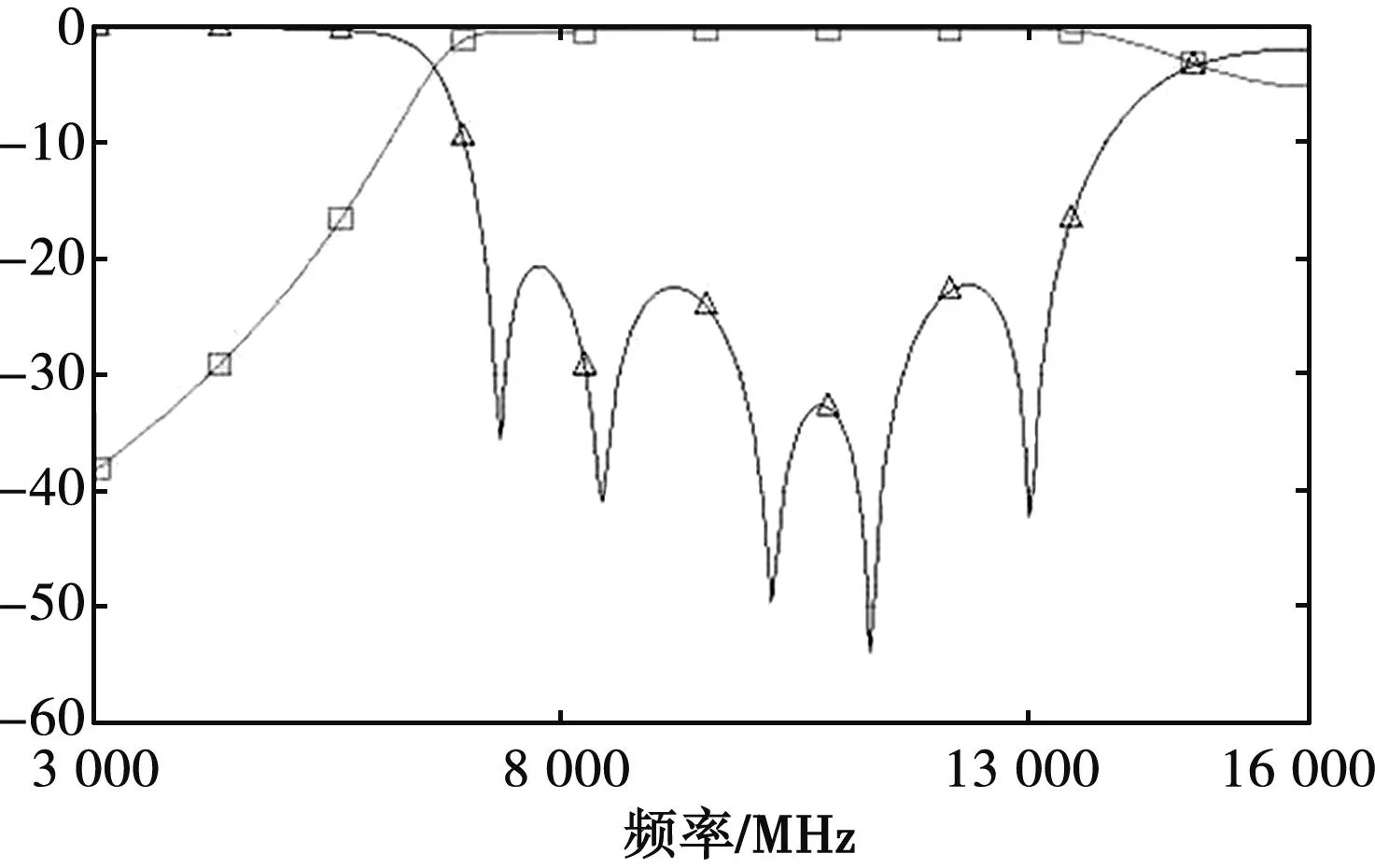
图6 全波仿真模型优化结果

4 滤波器实物测试

根据优化后的最终结果设置X频段微带滤波器尺寸,基于此完成实物制作,其实物和测试结果如图7、图8所示。

图7 滤波器实物图

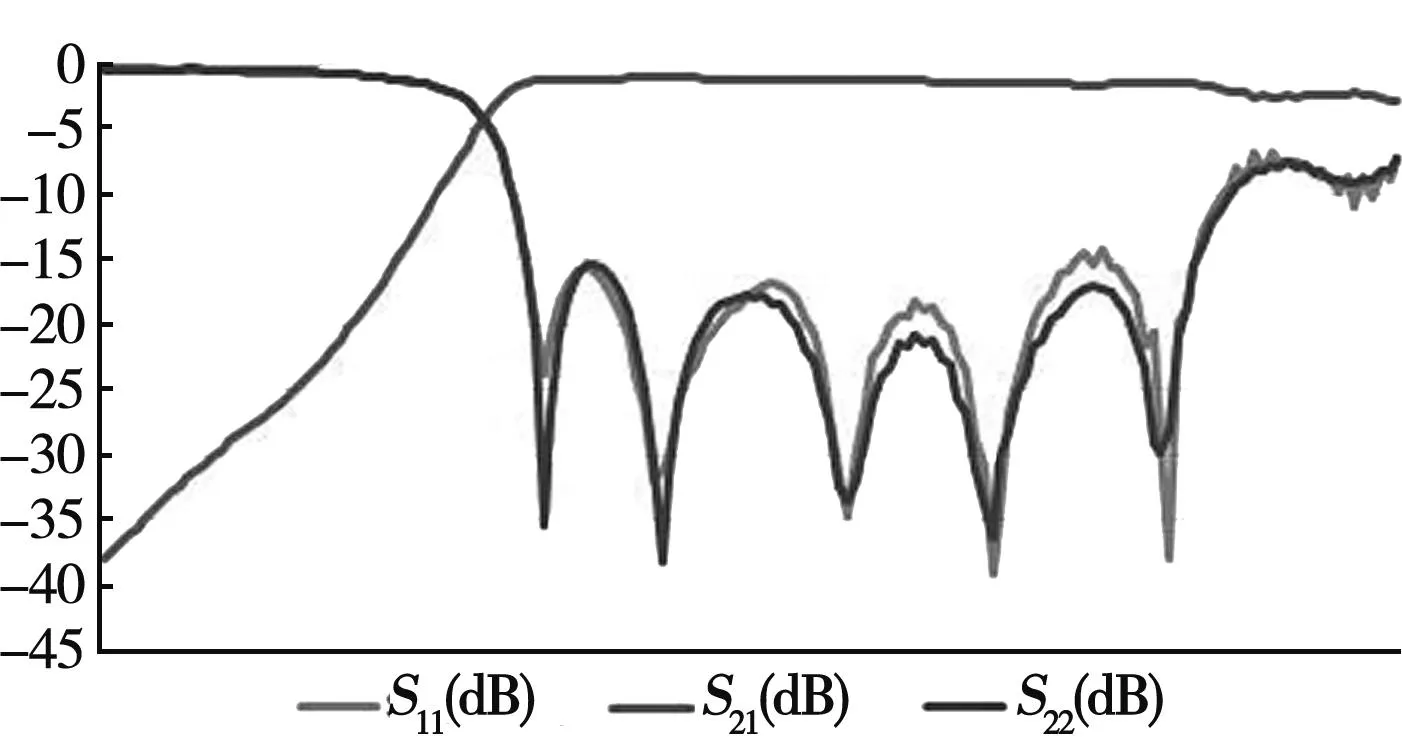
图8 滤波器实测结果

实测通带内插损小于1 dB,回波损耗小于-14 dB,实测结果比仿真结果插损偏大,且高频处反射参数恶化,这是因为在实物测试时,滤波器两端装配有SMP连接器,从而带来损耗,且会引起反射参数变化,同时加工误差以及人工组装不成熟也会引入一定的误差。

5 结束语

本文采用空间映射法设计了一款X频段微带滤波器,选用HFSS软件进行建模作为其精确模型,AWR软件建模作为其粗糙模型,两者相结合,从而快速优化得到合适的滤波器物理尺寸,并制作出实物,给出其实测结果,满足工程需求。