基于NOFRFs的非等温CSTR同步周期操作的评估优化
张亚东, 史洪岩
(沈阳化工大学 信息工程学院, 辽宁 沈阳 110142)
一直以来,化学反应器的周期操作是否能够提高化学反应过程的性能(转化率提高、可选择性增加等)受到研究者的广泛关注[1-5].至今,对周期操作的研究已经覆盖了很多不同类型的反应体系,如聚合反应、气固催化反应和电化学反应等.一般通过在稳态输入上加上强迫幅值、频率和波形等策略开展实验和仿真研究,研究目标主要是如何选择操作参数并证明其有效性[1].研究表明:相较于最优稳态操作,周期操作在一定条件下可以改善系统的时均性,对选择性、转化率和产量等有不同程度的提高[2-3].特别是对于非线性系统,这种非稳态操作可能产生比最优稳态操作更好的性能[4-5].连续搅拌反应釜(continuous stirred tank reactor,CSTR)本身具有显著的非线性,因此对CSTR周期操作的评估和优化成为现阶段工业应用亟待解决的关键问题.
英国Shiefld大学Lang等[12]从Volterra级数出发提出了非线性输出频率响应函数(nonlinear output frequency response functions,NOFRFs)概念.该方法允许以分析线性系统的方式分析非线性系统,能在一维空间上清晰准确地反映出系统输出频谱和非线性参数之间的关系,从而方便用图表进行分析,已被广泛应用于系统故障诊断等领域[13-14].Shi等[15]研究将NOFRFs应用于化学反应器单变量周期操作的评估与优化中,证明该方法能够快速有效地进行系统评估.付宥铭[16]过水吸收二氧化碳反应的实验验证了NOFRFs方法对二氧化碳吸收量估值的准确性.然而,实际化工过程都是多变量的非线性系统,且变量之间往往存在复杂的耦合关系,如何对多输入的非线性化工过程进行有效评估成为新的研究热点.
基于NOFRFs方法的优点,本文将通过同步操作入口浓度和入口温度两个参数,对非等温CSTR的输出浓度进行多变量周期操作,并和NFR方法以及单变量NOFRFs方法进行比较.结合遗传算法对神经网络拟合得到的函数进行寻优,找到全局最小值来进行系统设计,从而指导反应器的高效运行.
1 多输入非线性系统NOFRFs理论及同步周期操作评估方法
1.1 多输入非线性系统NOFRFs理论
对于稳定在零平衡的多输入非线性系统,假设xi(t)(i=1,…,m)和y(t)分别是非线性系统的输入和输出,系统输出的Volterra级数形式为:
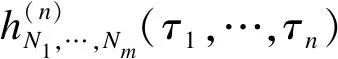
(2)
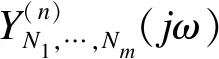
exp[-j(ω1τ1+…+ωnτn)]}dτ1…dτn
(3)
表示非线性系统的广义频率响应函数(general frequency response functions,GFRFs);
(4)
基于式(2),Peng等[17]定义多输入非线性系统的NOFRFs为
(5)
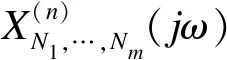
(6)
显然,利用多输入非线性系统的NOFRFs概念,式(2)可以写成
(7)
进一步将式(7)展开成多项式的形式为
(8)
多项式每阶项数为
C(n,m)=(m+n-1)…(m+1)m/n!,
n=1,…,N.
(9)
基于此,非线性系统的输入输出关系表示为
(10)
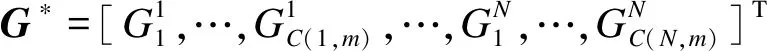
1.2 基于NOFRFs的同步周期操作评估
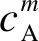
假设非线性系统的最高阶为2N,围绕稳态值xs、zs建立同步输入谐波
x(t)=xs+Acos(ωFt) ,
(11)
z(t)=zs+Bcos(ωFt+φ).
(12)
对由公式(1)表示的非线性系统1进行同步周期操作,系统输出频率响应可以表示为基波、无穷项高次谐波和非周期项的Volterra级数形式.
(13)
yDC是非线性输出响应y(t)的直流分项,是非线性化工过程周期操作评估的衡量指标,由输入单独作用和交叉效应的直流项组成,可以通过NOFRFs在零频时由系统非线性引起的输出响应来表示.
yDC=yDC,x+yDC,z+yDC,xz=Y(0)-ys.
(14)
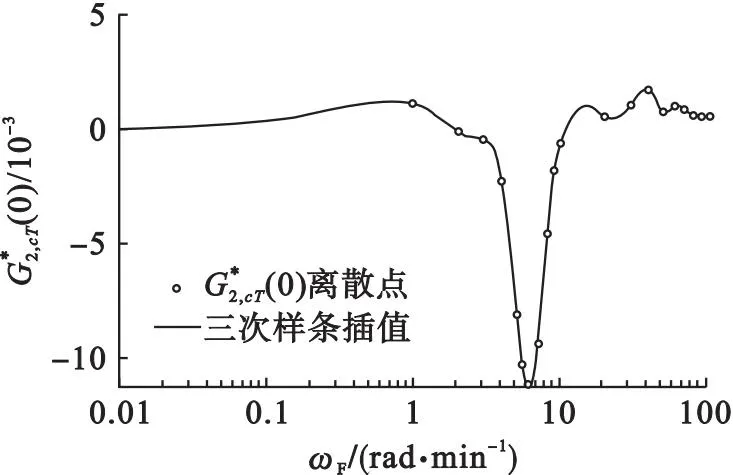
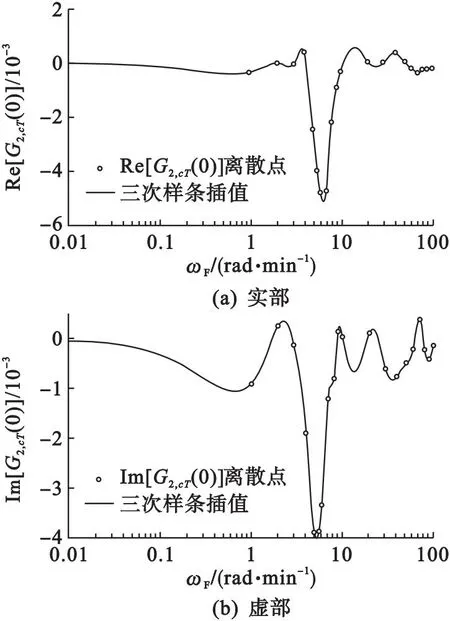
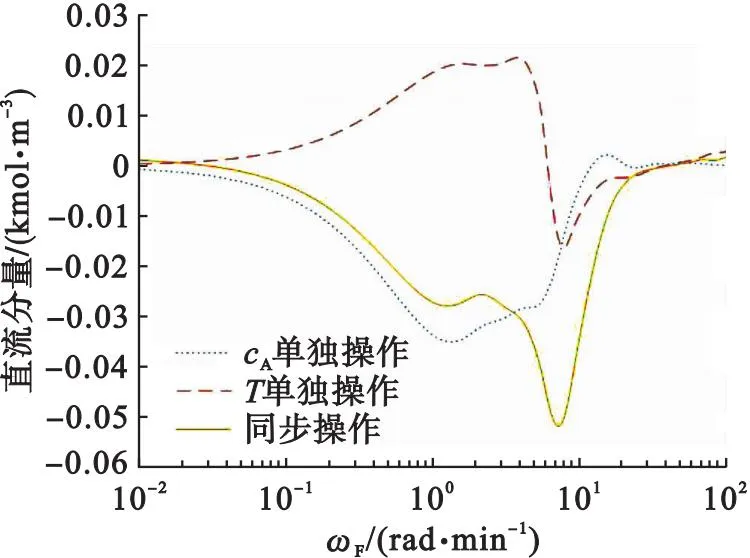
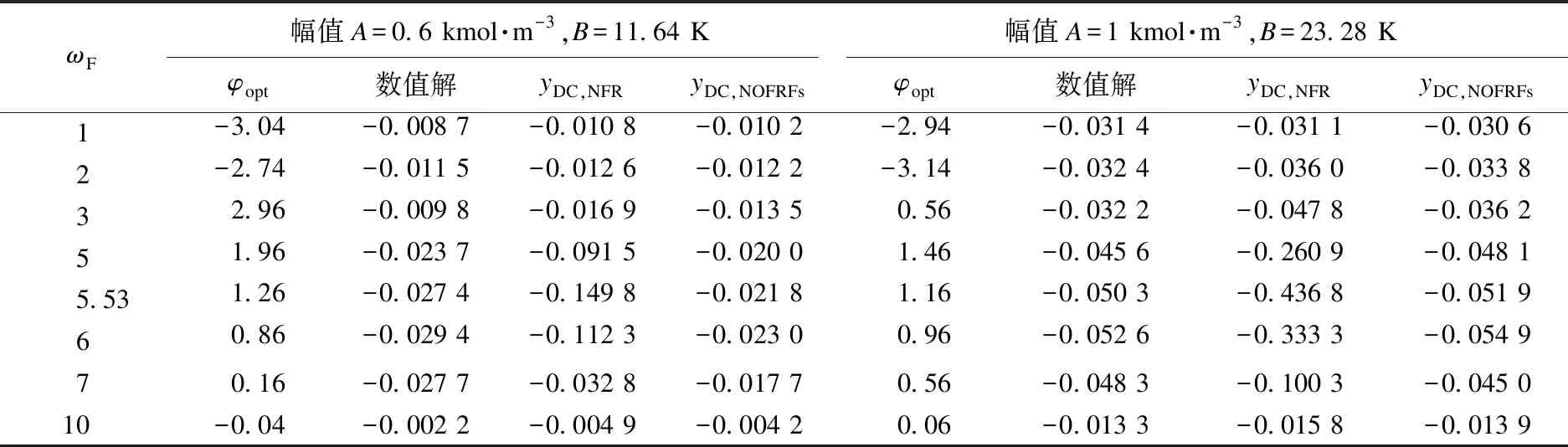
在M组不同幅值(A,B)谐波的激励下,其中M≥C(2,2)+C(4,2)+…+C(2N,2),且0 yDC=U*G*. (15) 式中:yDC=[yDC,1,yDC,2,…,yDC,M]T; U*= (16) G*=(U*TU*)-1U*TyDC. (17) 根据G*的函数关系,可以对式(17)进行最小二乘法求解.这种方法可以外推到具有3个或更多输入变量的非线性系统.基于NOFRFs的同步周期操作评估流程如图1所示. 图1 基于NOFRFs的同步周期操作评估流程 (18) 考虑一个典型的非等温CSTR中的非线性n阶反应A→product,物料和能量平衡方程为: (19) (20) 模型参数参见文献[18].入口浓度cA,i和入口温度Ti围绕先前建立的稳态cAi,s和Ti,s以余弦谐波形式进行同步周期操作. cA,i(t)=cAi,s+Acos(ωFt), (21) Ti(t)=Ti,s+Bcos(ωFt+φ). (22) 从A∈[0.2,2] kmol·m-3、B∈[3.23,48.45] K中选取幅值,在ωF∈[0,100] rad/min的范围内对由公式(19)和(20)表示的非线性系统进行同步周期操作,得到各阶NOFRFs.考虑4阶及以上的各阶NOFRFs对系统的影响很小,可以忽略不计.与出口浓度相对应的入口浓度和入口温度单独贡献的2阶零频NOFRFs与对数频率ωF的关系如图2所示.在5.78<ωF≤10.68 rad·min-1的频率范围内,G2,c(0)<0,G2,T(0)<0,二者的单独贡献为负,表明性能的提高可以通过引入单变量周期操作运行来预期. 图2 与出口浓度对应的入口浓度和入口温度单独贡献2阶NOFRFs 图3 与出口浓度对应的入口浓度和温度交叉效应的总的2阶NOFRFs sinφIm[G2,cT(0)]}. (23) 图4 与出口浓度对应的入口浓度和温度交叉效应的2阶交叉项NOFRFs的实部和虚部 图5给出了当A=50%、B=20%时,入口浓度和入口温度单独操作和同步周期操作的出口浓度评价指标直流分量的数值仿真的比较结果.在5.18<ωF≤25.25 rad·min-1的频率范围内,同步操作的出口浓度直流分量值明显小于入口浓度或者入口温度的单输入操作,说明同步操作的效果较好. 图5 入口浓度和入口温度单独操作和同步周期操作的出口浓度评价指标直流分量的数值仿真结果比较 表1给出了本文所提出的在入口浓度和入口温度同步周期操作下NOFRFs方法与NFR方法[11]的数值结果比较.从表1可以看出:基于NOFRFs的方法得到的结果与数值解吻合更好,说明了基于NOFRFs的新方法的准确性. 表1 同步周期操作下NFR和NOFRFs数值结果比较 表1的评估结果表示关于周期操作参数A、B、ωF和φopt与yDC,NOFRFs之间的离散关系,为了更好地指导实际操作,需要拟合得到在约束条件下关于周期操作参数A、B、ωF和φopt与yDC,NOFRFs之间函数关系,进而对系统进行优化设计.为得到非等温CSTR入口浓度和入口温度的同步周期性操作的最大转换率,需要找到周期性操作A、B、ωF和φopt之间的最优值.当入口浓度和入口温度进行周期性同步操作时,分别选择ωF∈[1,10] rad·min-1作为与yDC负值相关联的有效频率范围的频率边界,分别选择A=10%和B=1%作为有效振幅范围的最小输入振幅,选择A=100%和B=15%作为有效振幅范围的最大输入振幅.基于多输入非线性系统的NOFRFs的离散数据,通过神经网络拟合得到了yDC与周期运行参数A、B、ωF和φopt之间的函数关系f(A,B,ωF,φopt),具体算法如下: (1) 数据集:以A、B、ωF和φopt为输入数据集,NOFRFs方法得到的yDC为输出数据集; (2) 验证和测试数据,训练数据集为样本70%,验证和测试数据集各15%; (3) 神经网络体系结构.神经网络包含三个层次,输入层有4个单元,设置拟合网络隐藏层的神经元的数量为10,输出层有1个单元; (4) 采用Levenberg-Marquardt训练算法训练数据集,得到一个参数数据集的MATLAB函数. 表2给出了神经网络拟合结果,均方误差接近于0,R值接近1表示密切,说明基于多输入非线性系统的NOFRFs的离散数据具有很好的拟合度. 表2 神经网络拟合 基于遗传算法对神经网络拟合得到的函数进行寻优,找到全局最小值,函数为 minf(A,B,ωF,φopt), (24) 基于式(24)得到全局最小值yDC,min,反应物的稳态转换率δA,s、周期操作的最大转换率δA,pmax以及转换率增量ΔδA定义为: (25) 表3给出了最优值yDC,min和转换率的结果.结果表明:与稳态操作相比,周期操作下反应物的转化率有了明显提高. 表3 入口浓度和入口温度同步周期操作的最优值和转换率的结果 本文提出了一种基于多输入同步周期操作的NOFRFs的方法.该方法运用了多输入非线性系统的NOFRFs的思想,对非等温CSTR入口浓度和入口温度同步周期操作进行了快速评估.与NFR和单变量NOFRFs的方法进行对比,证明了该方法的快速性和准确性.此外,利用神经网络与遗传算法对本文方法产生的同步周期操作输入输出数据进行了优化设计,结果表明与稳态运行相比,优化参数使周期运行下反应物的转化率有了明显提高.

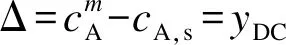
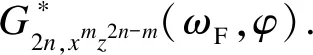
2 仿真结果与分析
2.1 非等温CSTR同步周期操作的NOFRFs分析

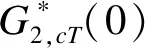
2.2 仿真结果
2.3 基于NOFRFs的优化设计


3 结 论

