基于动态故障树理论化工企业事故危险性分析

高梓涵, 张福群

(沈阳化工大学 环境与安全工程学院, 辽宁 沈阳 110142)

在我国,化工已经被视为国家经济的命脉之一.随着我国经济的逐步发展、化工产品的普遍化,人们对化工产品的依赖也逐渐增强,大到军事用品、航空材料,小到我们的生活日用品等[1].化工产品消费的提高,使得化工行业快速成长.但是传统化工行业的生产工艺复杂、安全隐患大,使得化工企业的事故预防工作十分复杂.只有全面分析和管理化工行业的风险,进一步研究和完善已建立的化工事故风险评估体系,才能有效地预防事故的发生[2].传统故障树需要准确了解潜在事件的发生概率,并且对具有动态特征的故障无法评估,而实际化工系统具有模糊性和动态性,传统的故障树方法已不适用于现代工业系统的故障诊断,因此,需要与其他技术方法相结合以提高该方法的适用性[3].为了描述和分析动态系统,弗吉尼亚大学的Dugan教授于1992年扩展了静态故障树(SFT)模型,用于空间站和空中交通管制动态系统的可靠性分析,并提出了动态故障树(dynamic fault tree,DFT),弥补了静态故障树应用范围较窄的不足.运用安全分析的科学方法和基本原理,使企业的安全管理向科学化、规范化、有序化的方向发展,确保经济安全稳定运行和可持续发展.

本文采用动态故障树分析法,对合成氨工艺中存在的中毒事故危险因素进行分析,通过分析确定底事件相对于顶层事件的重要度及影响,精确计算事故发生的概率,并进行有效预防.通过对繁琐故障树的简化,在不影响最终结果的前提下,极大地减少了计算量.与传统的故障树方法相比,动态故障树分析法适用范围更广.

1 动态故障树方法简介

动态故障树方法(DFTA)是指至少包含一个动态逻辑门的故障树,并在传统故障树基础上进行扩充.它结合了故障树分析和马尔可夫链方法的优点,是解决具有动态特性系统可靠性分析的有效方法.二叉决策图(binary decision diagrams,BDD)是近年来开发的一种新的故障树分析方法,它源于Shannon定理.BDD方法在解决一些复杂的故障树问题以及计算顶事件概率方面非常有效,比其他方法快得多,并且可以有效地解决原始故障树分析所面临的问题.通过将故障树转换为仅包含底部事件而不依赖中间事件的图形,BDD的布尔函数可以直接用于定性和定量分析.首先,对动态故障树进行模块化,以获得独立的静态子树和动态子树;然后,分别通过BDD图法和马尔可夫过程法求解[4].与其他方法相比,动态故障树方法在解决生产过程中动力学复杂、事故种类繁多的化工系统诊断问题上具有更大的优势.因此,本文选择动态故障树分析方法来诊断化工设备的故障.下面以某化工企业中毒事故为例,建立动态故障树模型并进行风险分析.

2 企业中毒或窒息事故危险性分析

确定故障树的顶事件为转化单元发生中毒或窒息事故.该事件是在有毒气体泄漏而未及时控制泄漏事件的情况下发生的.考虑到系统的复杂性,综合多方面的因素,建立毒气泄漏事故的动态故障树,该故障树由静态逻辑门的与门和或门以及动态逻辑门优先与门(PAND)组成(见图1).

T—中毒或窒息; G1—泄漏; G2—未及时控制泄漏事件; G3—腐蚀; G4—未发现; G5—控制失误; X1—存在有毒气体;X2—人失误; X3—材质不合格; X4—催化剂结碳,炉管烧穿; X5—焦炉气中含有硫化氢; X6—副反应生成物中含有二氧化碳;X7—生成物中含有氢气; X8—加入二段炉的空气中有氮气; X9—无报警器; X10—报警器故障; X11—通风条件差;X12—设备故障; M1—动态子树模块; M2、M3—静态子树模块.

2.1 基于BDD的危险性分析

由于M2、M3模块底事件较多,过程比较复杂,因此,需要将原有故障树转化为相应的仅含底事件的BDD,并确定M2、M3的最小割集合,通过这种方法计算顶事件的失效概率.

(1) G3静态子树对应的BDD如图2所示.在BDD中,底事件{X5}、{X6}、{X7}、{X8}为中间节点.通过BDD求解单调关联故障树最小割集的过程如下:

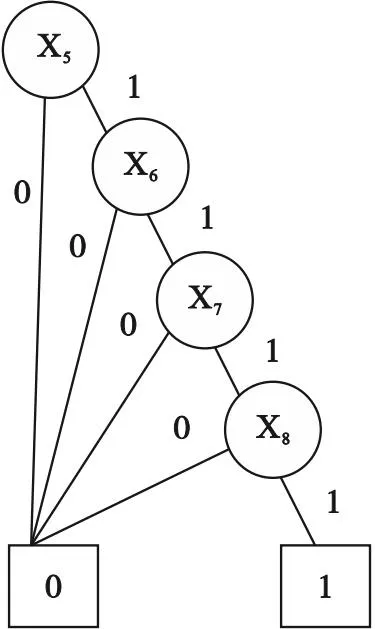
图2 G3对应的BDD

① 搜索BDD中从根节点到叶节点为1的路径,则图2中叶节点为1的路径为X5、X6、X7、X8.

② 对BDD进行分析可得:静态子树G3的割集为{X5}、{X6}、{X7}、{X8}.

由于X5故障概率为3×10-6/h,X6故障概率为10-5/h,X7故障概率为10-3/h,X8故障概率为3×10-4/h,则顶事件G3故障概率为1.01×10-5/h.

(2) M2静态子树对应的BDD如图3所示.在BDD图中,底事件{X2}、{X3}、{X4}、{G3}为中间节点.通过BDD求解单调关联故障树最小割集的过程如下:

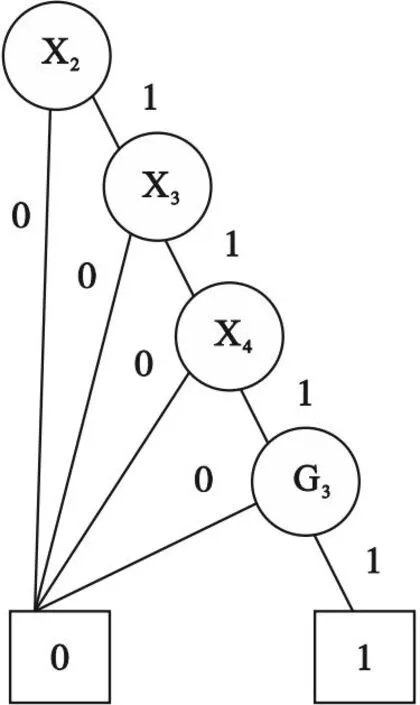
图3 M2对应的BDD

① 搜索BDD中从根节点到叶节点为1的路径,则图3中叶节点为1的路径为X2、X3、X4、G3.

② 对BDD进行分析可得:静态子树M2的割集为{X2}、{X3}、{X4}、{G3}.由于X2失效概率为10-5/h,X3故障概率为3×10-4/h,X4故障概率为10-4/h,G3失效概率为1.01×10-5/h,则静态子模块M2的失效概率为3.21×10-4/h.

(3) M3静态子树对应的BDD如图4所示.底事件{X9}、{X10}、{X2}、{X11}、{X12}为中间节点.通过BDD求解单调关联故障树最小割集的过程如下:

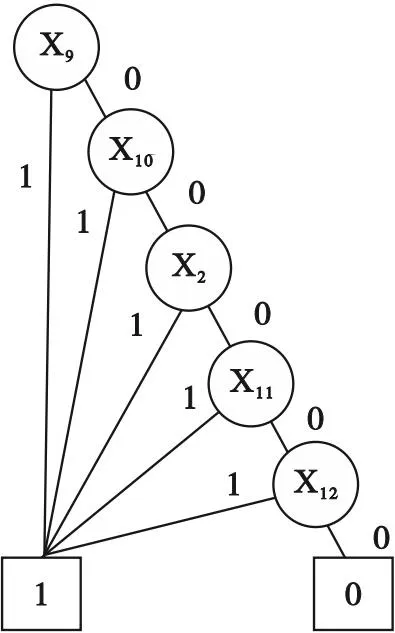
图4 M3对应的BDD

搜索BDD中从根节点到叶节点为1的路径,则图4中叶节点为1的路径为X9、X10、X2、X11、X12,则静态子树M3的割集为{X9}、{X10}、{X2}、{X11}、{X12}.M3失效概率为7.1×10-5/h.

2.2 基于马尔科夫模型的危险性分析

由于转化单元中含有动态逻辑门,所以不能采用传统的故障树分析法进行分析,而是采用构建马尔科夫模型这一方法进行分析.

从图1中可以看出,M2、M3为静态故障子树,M1为动态子树.用马尔科夫链法进行分析,动态子模块M1及相应的马尔可夫转移链如图5所示.利用马尔科夫过程分析图5中的动态故障树,在该马尔可夫链转移图中, 000状态表示正常运行状态, Op表示毒气泄漏事故未发生,Fa表示发生毒气泄漏事故.每次事件都是相对独立的,并且只有Op、Fa两种工作状态.

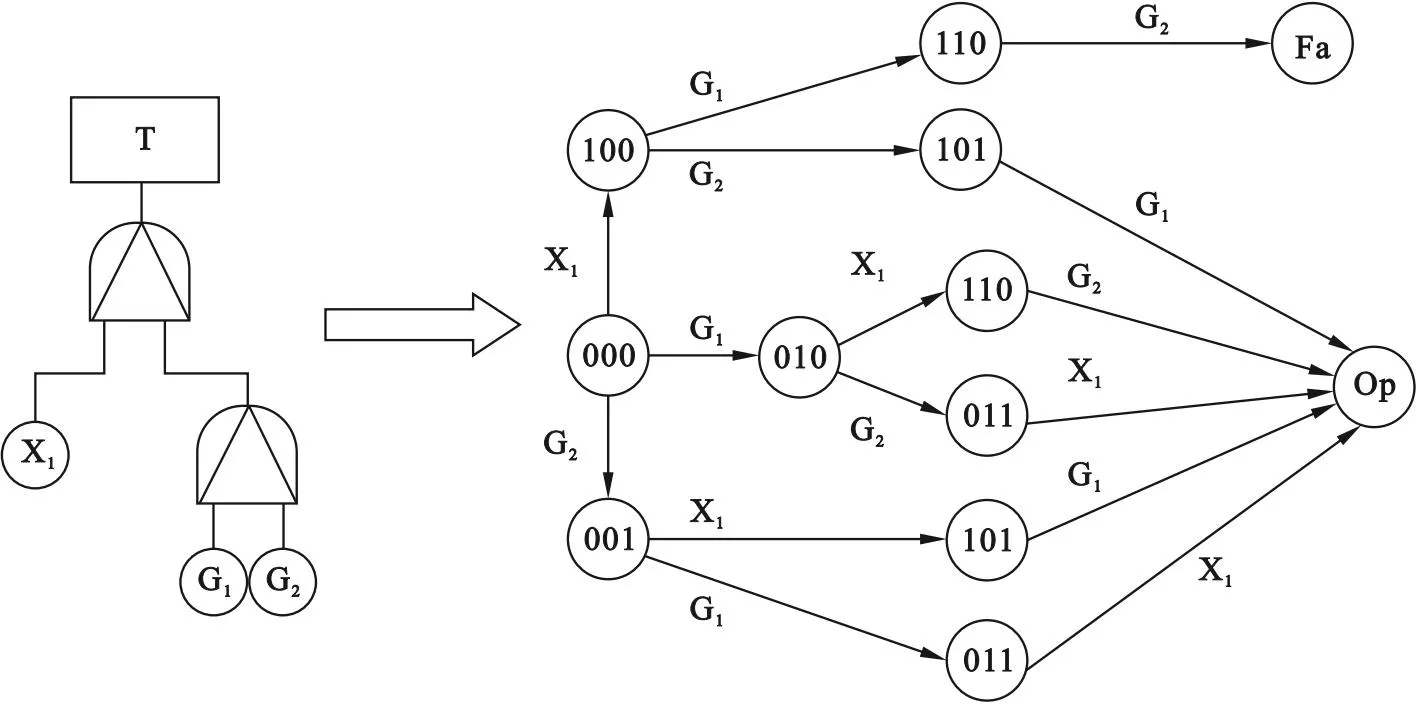
Fa—故障;Op—正常.

在图5中,从故障状态回溯,得到马尔科夫链000→100→110→Fa.

由此得到动态子树的故障模式为

X1→G1→G2.

综合以上结果,对故障子树进行合成运算,针对较为复杂的系统可以使用割序法列出系统的结构函数,运用时间规则得出系统失效模式.

由于X1故障概率为3×10-4/h,G1故障概率3.21×10-4/h,G2失效概率为7.1×10-5/h,则顶事件T发生概率为1.129×10-4/h.

3 结束语

通过上述分析计算可知:首先,将动态故障树进行模块化分解成静态子树和动态子树;然后,分别利用BDD和马尔可夫链进行分析,并通过计算得出各模块在系统中的发生概率,得出该系统的失效模式.由各个模块的BDD及马尔科夫链图分析得出,底事件X1的危险性最大,其次是X2的危险性大,在生产中要特别注意对X1、X2的安全防护.

现代工业生产过程的运行模式种类繁多,运用有效的故障检测技术能够保证生产的正常进行[5].传统故障树作为安全评价方法的一种,有着灵活性、直接性、适用范围广等优点,但是其本身有一定局限性.本文在传统故障树的基础上同时引入模块化的概念,提出构建动态故障树以对化工系统中中毒或窒息事故进行诊断分析.该方法既可以包含传统故障树优点,又能够处理含有动态逻辑门的复杂性故障树问题,能够更好地解决化工行业实际生产过程中出现的各种问题.