数学表达：培养推理意识的关键路径

文∣刘飞 于蓉

数学表达是数学问题思考过程与结论外显的手段。学生数学表达能力的强弱，反映了学生推理意识发展程度的高低。数学表达能力是学生认知能力中的一种。优秀的数学表达能力，能清晰体现学生的良好思维水平，能帮助学生内化思维模式。培养数学表达能力是推理意识发展的重要途径，也是培养推理意识的关键，使学生养成良好的思维习惯。

一、课堂教学中数学表达存在的问题

(一)学生表达意愿的缺失

如果教师抛出数学问题却常常无人作答，这其中主要有两种原因：一是学生不愿思考、不会表达；二是学生愿意思考，却不想或不敢表达。出现这种现象的根本原因是课堂缺乏良好的学习氛围，学生缺乏表达的素材，这些都遏制了学生表达欲望的产生，从而限制了学生推理意识的萌发。

(二)学生表达方法的单一

在课堂上，教师往往采取这样的提问方式“这个问题你来说一说……你说……谁再来说一说……”，学生的表达就在这样的课堂提问状态下结束了。单一的数学表达方式，限制了学生的思维宽度，降低了学生表达的欲望，阻碍了学生推理意识的发展。

(三)教师对学生表达过程的无视

学生在课堂上回答问题时，教师常常会紧抓学生表达结果的正确性，而忽视学生的数学表达逻辑是否清晰、思考过程是否合理等问题，对学生表达中存在的问题缺乏及时的反馈，自然影响学生理性思维的塑造。由于教师对学生数学表达过程的无视，学生无法意识到表达过程存在的问题，也就难以形成缜密的逻辑思维，这就限制了学生推理意识的进一步发展。

二、培养数学表达能力，是发展推理意识的重要途径

(一)激发表达欲望，助力推理意识萌芽

推理是表达的前提，表达是推理的外显。当学生具有强烈的表达欲望时，就会主动思考，积极进行问题的推理，让推理意识萌发。因此，教师要关注学生表达情感的培养，激发学生的表达欲望。教师可在课堂中创设情境、设计有趣的问题，启发学生的思考，激发其表达的欲望，促进其推理意识和学习内驱力的形成和发展。同时，要让学生有话可说，就要让学生有足够的表达素材，素材既可以是教师提供的，也可以是学生主动获得的。

以“圆的认识”教学为例。在教学时，为了让学生感受圆在生活中的广泛应用，可以创设符合学生生活实际的情境并设计有趣的问题，促使学生有意识地推理。

【情境一】

师：为什么车轮都是圆形的呢？有人知道吗？

生1：因为圆形车轮行驶起来更加平稳、舒适。

生2：假如车轮是长方形，车子行驶时就会很颠簸，起起伏伏。

师：我们来做个实验吧！(演示车轮在运动过程中的车轴轨迹)

师：知道是什么原因了吗？

车轮之所以能让车子平稳行驶，同学们知道是圆的什么特征在起作用吗？

生：车轴位于圆心，它到地面的这一段是半径，半径都相等，所以车子行驶起来很平稳。

【情境二】

师：为什么井盖一般都设计成圆形呢？我们也来做个实验。

老师设计了三个不同形状的井口和配套的井盖，请同学到前面来感受一下它们的区别。

图1 不同形状的井盖

师：圆形井盖和其他形状井盖相比，不容易掉，是什么原因？

生1：三角形和平行四边形的井盖，有的地方比较窄，井盖就可能会从井口宽的地方掉进去，这样设计不好。

生2：圆形的井盖宽度比较均匀，所以不容易掉进去。

师：宽度都均匀，也就是什么都相等？

生：圆的直径都相等。

在这一教学过程中，教师通过创设真实的情境，营造良好的课堂氛围，以生活中的井盖等为例为学生提供有价值的表达素材，让学生在说一说、辨一辨、做一做的过程中，有意识地推理车轮、井盖的设计与圆的特征之间的联系。良好的课堂氛围充分激发了学生的表达欲望，促进了学生的思考和表达，使学生的推理意识得到萌发。

(二)注重表达和表征方法，促进推理意识形成

1.注重表达方式多样

数学表达的方式不仅仅局限于“说话”，还包括了倾听、阅读、书写等。[1]因此，要促进学生推理意识的形成，可以将多样表达方式作为驱动，让学生在不同的数学表达方式下有条理地思考。

以“解决问题的策略(从问题想到)”的教学为例，让学生经历倾听同学说、自己说和写一写的过程，通过严谨的推理理清解题的思路。

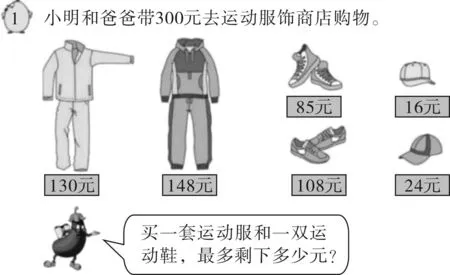
图2 “解决问题的策略”的教学例题

师：要求最多剩下多少元，你是怎么想的？

生1：买的东西要最便宜。

生2：两样物品都买最便宜的就可以了。

师：其他同学还有补充的吗？

生3：带的钱，减掉最便宜的衣服和鞋子钱，就是最多还剩的钱。

师：你能把想到的数量关系表示出来吗？

生1：300元-运动服的130元-运动鞋85元=最多剩下的钱。

生2：300元-(运动服的130元+运动鞋的85元)=最多还剩的钱。

师：请尝试列式解答。

学生在自己说一说和倾听同学说的过程中，逐渐理解题意并完善语言表达，最后通过写一写，建构基础的数学模型，积累推理经验。

2.注重表征方式多元

数学表达是用来表征思维的，而多元的表征方式更能凸显学生的思考过程，帮助学生分析和解决问题。数学表征包含语言、符号和图形等，利用这些表征方式，教师能够在教学中渗透简单的类比或归纳思想，帮助学生推理一些初步的结论。

以“加法交换律”的教学为例。在教学上，让学生通过多元表征，表达归纳发现，得到结论。

图3 “加法交换律”的教学例题

师：要求跳绳有多少人，我们得到了这样两个算式：28+17=45(人)、17+28=45(人)。这两个算式分别是求什么的人数？结果分别是多少？仔细观察，有何相同和不同。

生：相同点是加数和得数一样。不同点是两个加数的位置不同。

师：如果用符号将它们连接，可以用什么符号？(等号)

师：观察这些等式，你有什么发现？

生：加数位置换了，结果一样。

师：你想怎样表示这种规律呢？动手试一试。

生1：我是用图形来表示：○+△=△+○。

生2：我是用字母来表示：a+b=b+a。

生3：我是用文字来表示：甲+乙=乙+甲。

生4：……

师：刚才的规律，我们一般用第二位同学的方式来表示。

师：两个数相加，交换两个加数的位置，和不变。这就是加法交换律。

在表达运算规律时，可以先让学生说一说，再选择自己喜欢的表征方式，学生既可能选择用文字的表征方式，也可能选择用图形或者符号。学生通过不同的表征方式学会梳理发现，从而归纳推理出一般规律，促进了推理意识的形成。

(三)聚表达实质，促推理意识发展

在学生进行数学表达时，教师的反馈既要注重其结论是否正确，也要注重其表达是否规范、思考过程是否严谨。因此，可以从以下角度入手，发展学生的推理意识，提升学生的交流能力。

1.重视结论合理性，发展推理意识

学生在总结发现时，容易忽视结论是否正确，表达也不够缜密。因此，教师有必要通过用心设计，促使学生再思考、再表达，使学生的表达更加理性且严谨，与推理的严谨性相辅相成。

以“用计算器探索规律”的教学为例。在教学这一课时，可以培养学生的质疑精神，使其注重推理结论的合理性。

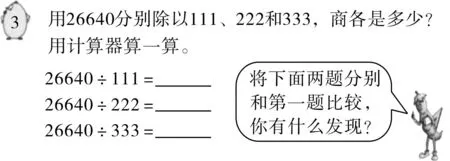
图4 “用计算器探索规律”的教学例题

师：刚才我们通过用计算器计算，发现怎样的规律？

生：在除法计算里，如果被除数不变，除数乘几，得到的商等于原来的商除以几。反过来说，得到的商等于原来的商乘几。

师：那么在其他乘法算式中是否也成立呢？我们应该怎么做呢？

生：我们还要再找一些例子来验证。

师：把例子写下来，用计算器验证。

生1：我举的例子是这样的：600÷5=120、600÷10=60、600÷15=40。

生2：我是这样举例的：26640÷666=40、26640÷555=48、26640÷444=60，和刚才计算的26640÷111=240放在一起比较，符合我们刚才的发现。

师：通过这两位同学的介绍，可以发现他们举的例子都符合这个猜想。你们举的例子也符合这个猜想吗？小组交流，说说发现。

师：有没有谁举的例子不符合这个猜想的？

生：没有。

师：通过进一步探究，看来我们的猜想是成立的。

在这一教学过程中，学生在得到猜想后，教师适时进行干预，判断猜想是否正确，由此激发了学生的进一步探究，让推理更深入，让学生再次表达思考过程，并感悟到任何一个结论都需要经历严谨的推理。

2.重视因果表达，发展推理意识

在数学教学中，教师要帮助学生认识已知条件和未知问题之间存在的因果联系，经历严谨的推理过程，厘清逻辑联系，从而有理有据地表达。以下面问题为例：

一桶水，丈夫独饮可饮14天，夫妻同饮可饮10天，若妻子独饮，则可饮多少天？

师：这个问题怎么解答，需要知道什么？

师：条件中隐含着怎样的信息？

生：我发现这句话中隐含着“丈夫4天所喝的水等于妻子10天所喝的水”这个信息。

生：这道题可以改写为一道等价的题目：丈夫4天饮水的量等于妻子10天饮水的量，那么丈夫14天饮水的量等于妻子多少天饮水的量？或者更简单一点：因为丈夫2天饮水的量等于妻子5天饮水的量，所以丈夫14天饮水的量等于妻子多少天饮水的量？在这种分析下，问题的解决便十分容易了：丈夫14天饮水的量等于妻子7×5=35(天)饮水的量。

师：妻子独饮这桶水，可饮35天。[2]

要解决这道题，必然要厘清条件的隐含信息，通过逐步的推理，学生明确“丈夫4天饮水的量等于妻子10天饮水的量”，推理出“丈夫2天饮水的量等于妻子5天饮水的量”。在解决问题过程中，学生清晰地表达出条件和问题之间的因果联系，让复杂的问题简单化，其表达能力得到了凸显，推理意识也得到了进一步的发展。

低学段学生的语言较为匮乏，思考能力有限，因此，可以重点关注低学段学生数学语言的训练。教师可以借由非常明显的具有因果联系的问题，引导学生使用因果关联词汇，如“因为……所以……”“如果……那么……”等。这些词汇能够帮助学生厘清思路，构建基本的数学语言表达模型，形成“有条理地思考，有根据地表达”的数学素养。[3]

(四)重表达过程，促推理意识生成

学生的数学表达存在着过程被忽视的现象，主要原因在于教师的课堂教学缺乏逻辑性和层次性。教师重结果不重过程，学生表达方面的问题得不到修正，其推理必然缺乏严谨性，推理意识难以在其大脑中落地生根。因此，在教学时，教师要重视学生的数学表达过程不断优化，以此促进学生推理意识生成和发展。

1.表达过程规范

学生在进行数学表达时，常常缺乏规范性的思考过程和表达语序。在教学上，教师要积极渗透各类思想方法，让学生思考时能有迹可循、有法可依。同时，要培养学生数学语言的缜密性，强调前后言语之间的逻辑性、完整性和合理性。

2.表达过程循序渐进

学生表达水平的提高并不是一蹴而就的，需要经历一个循序渐进的过程。不同学段的学生，生活经验和学习经验存在较大差异，所以在学生进行数学表达时，教师要立足学生已有的知识水平，提出满足当前需要的表达要求。同时，在表达过程中，要让学生通过其他同学的讲解、教师的指导等，学会对自己的表达内容进行改进，由浅入深、由易到难地优化表达过程，使推理意识在表达过程中层层递进、层层深化，逐步塑造思考过程，让推理意识作用于整个学习过程。

数学表达的过程伴随着理解性学习、高阶思维、主动倾听等深度学习的特质。[4]注重学生的数学表达，就是关注学生对学习过程的体验，让学生在数学表达的版式过程中，走向更深层次的数学思维，推动数学核心素养推理意识的发展。