基于改进禁忌搜索算法的立体车库搬运器路径优化建模与仿真
赵剑英, 李建国,2*, 薛千树
(1.兰州交通大学自动化与电气工程学院, 兰州 730070; 2.四电BIM工程与智能应用铁路行业重点实验室, 兰州 730070)
平面移动式立体车库采用与立体仓库类似的原理和结构,入/出库过程需要依靠搬运器转运车辆,研究搬运器作业路径与层列组合及顾客到达率关系,有助于提高车库运行效率。
左为恒等[1]以排队论为理论基础,分析立体车库车辆排队过程,根据车辆到达率的变化,采用一种将堆垛机的数量和运行速度综合考虑的调度方式,来降低立体车库的运行能耗;Ly等[2]以最小化运行时间为优化目标,讨论了自动导引搬运器系统(automated guided vehicle system,AGVS)在仓库运营中的存储分配策略和路径规划;Dong等[3]将四向穿梭车式密集仓储系统(shuttle based storage and retrieval system,SBS/RS)建模为离散马尔可夫链,推导出各策略组合下的往返分配,并进一步建立了单命令和双命令操作的预期旅行时间模型;Wang等[4]提出了一种将禁忌搜索和遗传算法相结合的混合算法来优化理论操作时间;改善算法的局部搜索能力的同时也不会损失多样性;Yu等[5]在对自动存取系统 (automated storage and retrieval system,AS/RS)输入输出分析的基础上,提出了一种混合禁忌搜索算法来解决存储分配问题;文献[6-7]分析了自动化导引搬运器(automated guided vehicle, AGV)运行环境,通过改进禁忌搜索算法优化全局搜索能力和收敛速度。文献[8-10]对立体车库和仓库在建设过程中的层列组合方式[8],建设成本[9-10]进行分析研究;文献[11-14]通过遗传算法[11]、改进遗传算法[12-13]以及粒子群算法[14]对立体车库的调度设备运行路径进行优化;许伦辉等[15]提出AGV动态路径优化的时间窗模型,以此避免AGV路径冲突;蔺一帅等[16]提出了智能仓储协同优化框架的求解算法,分析了货位与路径优化之间关系。然而,车库中层列组合的分布影响搬运器运行环境,诸多文献对自动化立体车库路径优化策略进行了不同深度的研究,但是综合考虑车库布局及顾客因素的路径优化方案研究较少。
在建立多条件约束的平面移动式立体车库搬运器最短服务时间调度模型基础上,考虑层列组合及顾客到达率影响因素,提出一种改进禁忌搜索算法,在初始解效率最优库位布局下进一步优化搬运器作业路径,以实例车库顾客泊车历史数据进行可行性验证,为提高立体车库运行效率提供参考。
1 平面移动式立体车库模型
平面移动式立体车库可以根据场地和高度的不同进行参数的设计,其主体部分包括升降机(lift)、有轨导引搬运器(rail guided vehicle,RGV)、钢构框架、载车板、入/出库口(input/output point,I/O)、电气控制系统等,其实体模型如图1所示,以I/O口所在层为分界线分为地上部分和地下部分。
研究对象属于AS/RS系统,其中RGV不仅可以水平移动还可以利用升降机进行跨层移动,入/出库口用于车辆的进出,RGV用于与泊位实现入/出库交换及车辆水平搬运。升降机(lift)主要用于对RGV及车辆进行跨层搬运。通过建立三维坐标系来描述RGV的运行场景,其中x轴表示RGV的水平移动方向,其值表示RGV所在位置的列坐标,y轴用来区分车位所在层,z轴表示RGV的垂直移动方向,其值表示RGV所在位置层坐标。
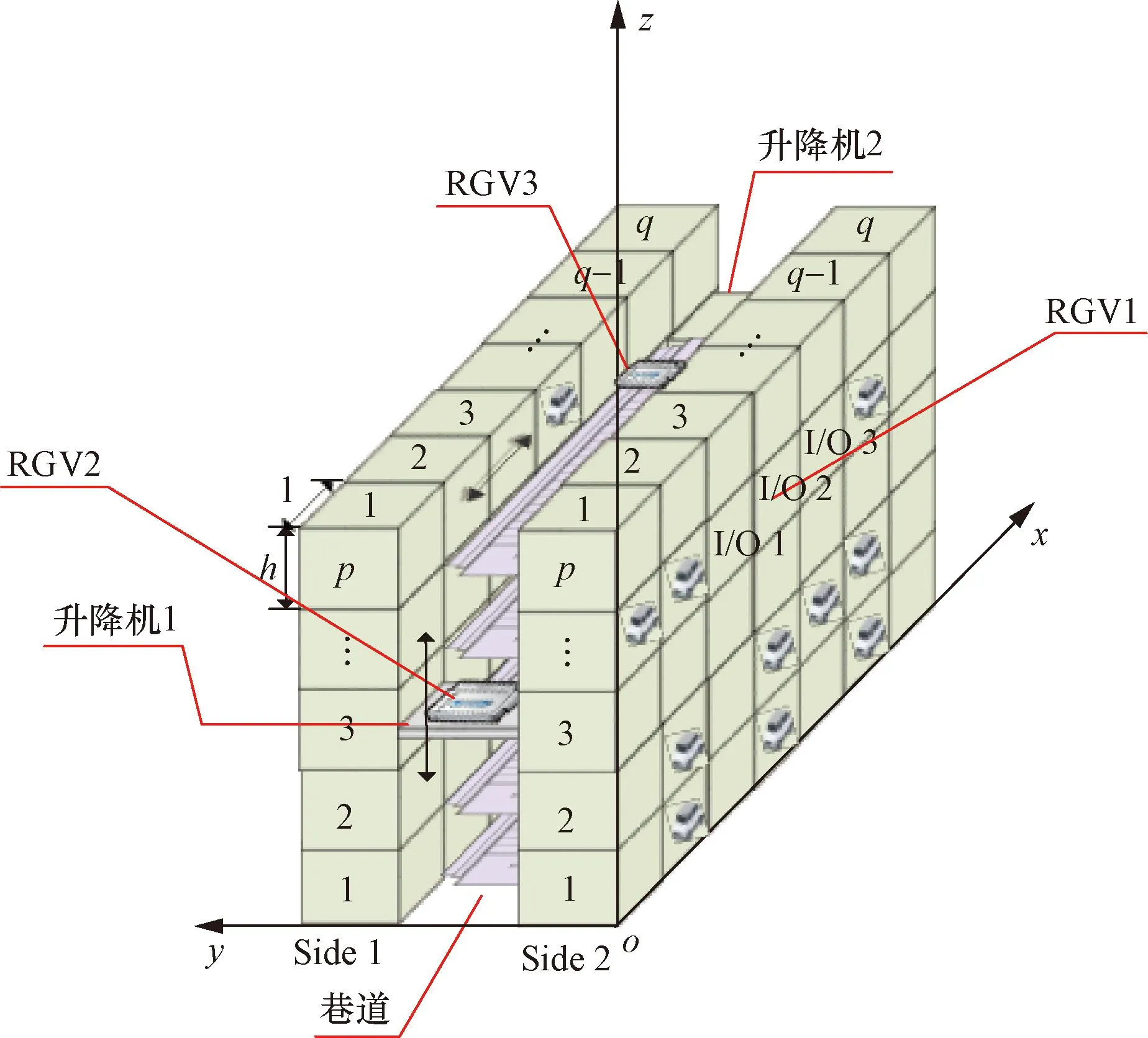
图1 平面移动式立体车库实体模型Fig.1 Solid model of flat mobile stereo garage
2 数学模型建立
2.1 配置条件
为表述方便,结合实际运行情况,以下为所研究平面移动式立体车库的配置条件。
(1) 车库车位分配策略为随机就近分配,即入库过程中为到达车辆选择一个离到达位置最近的空车位。
(2) 空闲RGV待命位遵循原地待命策略,即在未收到新的入/出库任务指令前,RGV停在最后一次入/出库任务的结束位置处。
(3) 车库中RGV、入/出库口及升降机的占用均遵循先到先服务规则。
(4) 忽略RGV、升降机的启动、制动时间及RGV进、出升降机时间。
(5) 同一时刻一个任务仅能调用一个RGV或一部升降机。
(6) 同一时刻车库中的一个路径节点仅被一个RGV占用,若同一时间同一节点发生多个RGV的冲突,则规定先收到指令的RGV先动作,其他进行等待直至其之前所有RGV完成操作。
2.2 基于服务时间最短的RGV调度模型
对于需要跨层搬运的入/出库任务,RGV的运行过程包括水平方向与垂直方向,其中,垂直方向需升降机配合,当升降机处于繁忙或者与当前任务不在同层时,就会增加作业的服务时间。根据RGV不同运行阶段场景及水平、垂直方向的运行时间分析,建立RGV完成入/出库服务所消耗时间最短的调度模型,其目标函数为
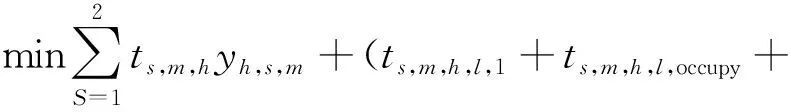
(1)
(2)
(3)
ts,h,l,occupy=ts,m,h,l,waite+ts,m,h,l,actual
(4)
式中:ts,m,h表示编号为m的RGV在任务h的S运行阶段的运行时间;S=1,表示RGV空载运行阶段;S=2,表示RGV负载运行阶段;ts,m,h,l,1(2)表示编号为m的RGV在任务h的S运行阶段自待命位置运行至升降机l所在位置(自升降机l所在位置运行至泊车位置)的运行时间;yh,s,m、zh,s,m为决策变量;ts,m,h,l,occupy表示编号为m的RGV在任务h的S运行阶段占用升降机l的运行时间;ts,m,h,l,waite表示编号为m的RGV在任务h的S运行阶段等待升降机l的时间;ts,m,h,l,actual表示编号为m的RGV在任务h的S运行阶段中升降机l的实际运行时间。
2.3 约束条件
考虑设备配置及安全问题,设置以下约束条件。
(1)RGV进入一段路径的起始时间和离开该路径的结束时间。
(2)每一个顾客任务只能使用一辆RGV。
(3)任务数不超过RGV配置总数。
(4)RGV运行最小安全距离。
计算公式为
(5)
(6)
(7)
(8)
(9)

2.4 改进禁忌搜索算法
禁忌搜索算法(tabu search,TS)基本原理为采用邻近域选优方法,并通过禁忌表记录状态变化,当出现被禁解优于当前最好解时,引入藐视准则,最终通过迭代实现路径寻优。
在2.2节基础上,针对禁忌搜索算法随机生成的初始解容易导致算法陷入局部最优解以及算法收敛速度较慢问题,对其进行改进,以求解立体车库周期最短路径问题。定义立体车库单位工作周期RGV路径转移过程为:RGV从待命位置前往I/O口或泊车位置进行当前任务作业,完成当前任务后前往下一任务起始位置。根据立体车库层列布局,建立C×F矩阵,初始禁忌长度为0,改进方法如下。
(1)以RGV服务时间调度模型构造初始路径Sij的目标函数,将约束条件转化为目标函数的惩罚项,将不符合约束条件的解惩罚,从而生成符合约束条件且服务时间最短的初始解。
(2)邻域结构定义为部分节点(不满足条件约束)与邻近节点互换产生新的邻近域N(Sij,n)。
改进后算法流程如图2所示。
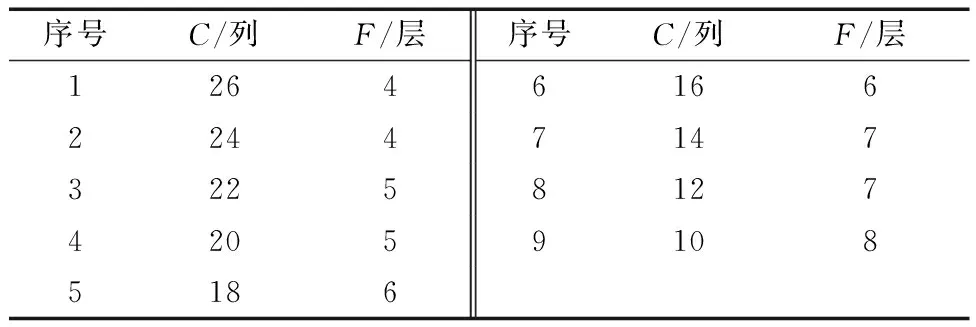
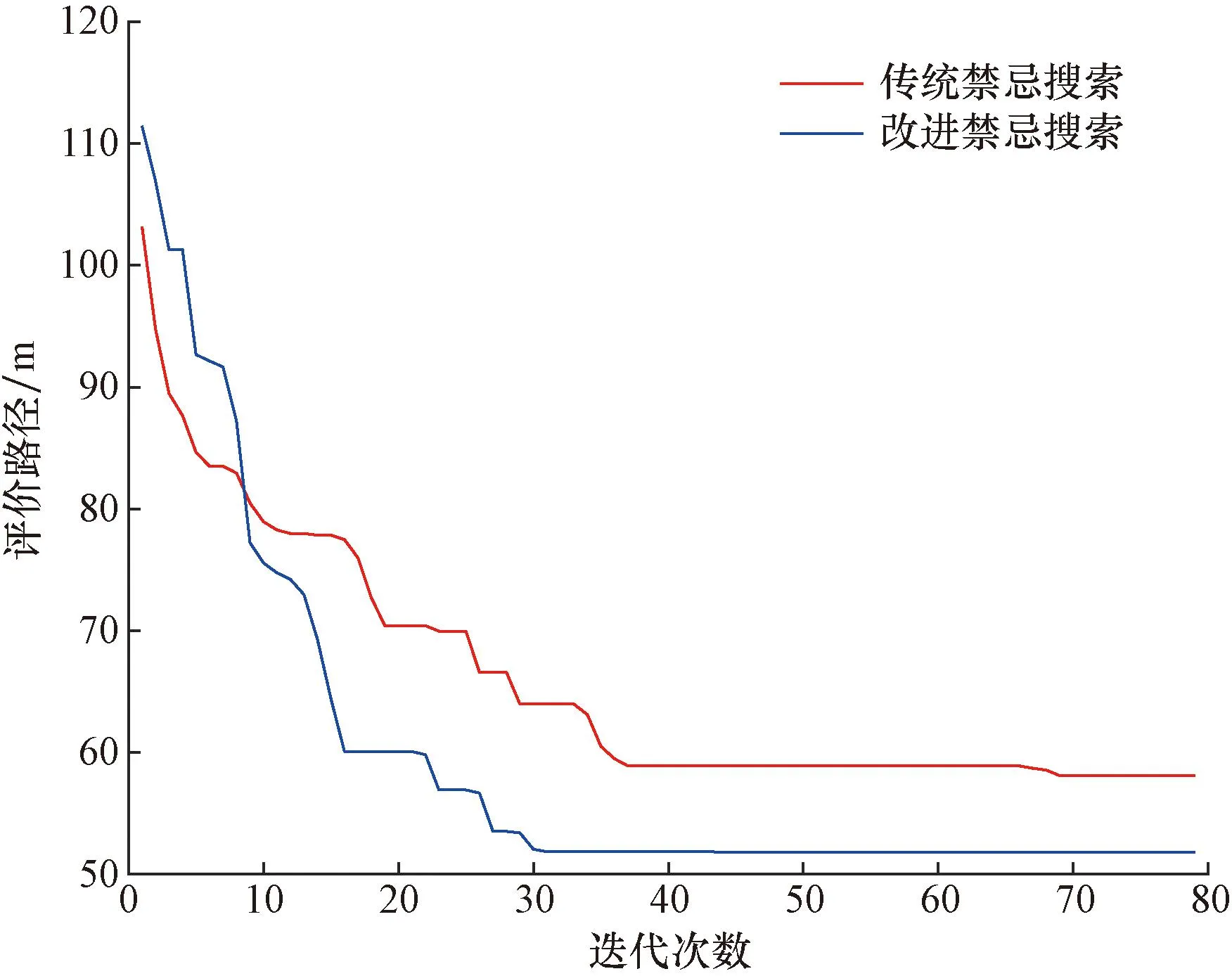
假设任务Oij初始路径Sij上的第n个节点Sij,n处不满足条件约束,主要表现为RGV间无法满足最小安全距离,及路径节点时间窗约束。针对该节点邻近域N(Sij,n)生成候选解Sreg。以式(1)作为评价函数,若Sreg>Sij,则更新最优值,反之,若Sreg 图2 改进禁忌搜索算法流程图Fig.2 Flowchart of the improved forbidden search algorithm N(Sij,n)={N|N=Sij,n+μ*Dm,l} (10) Dm,l∈{-1,+1} (11) 式中:μ为单位步长,其值小于RGV最大前瞻节点数;Dm,l为方向决策变量,由于RGV在轨道双向运行,即定义正方向交换为Dm,l=-1,反方向交换为Dm,l=+1。 以RGV平均服务时间、RGV平均利用率、RGV平均能耗作为运行效率评价指标。 (1) RGV平均服务时间Ts:由服务顾客总数与RGV服务总时间决定,其值越小说明车库的运行效率越高。计算公式为 (12) 式(12)中:Tij为任务Oij自开始服务至服务结束所用时间;N为入库车辆的总数;N′为出库车辆的总数。 (2) RGV平均利用率Tρ:表示车库1 d中RGV的平均繁忙程度,相同规模车库,服务相同的顾客数量,则RGV平均利用率数值小表明入/出库效率越高,对车库运营者越有利,计算公式为 (13) 式(13)中:T′ij为RGV执行任务Oij空载运行阶段时间;T″ij为RGV执行任务Oij负载运行阶段时间;To为RGV执行1次存取所需时间,h为任务Oij的编号;Dij为RGV执行待命任务耗时;Tz为车库1 d中运行总时间,m=1,2,…,M,M∈N+为RGV的编号。 (3) RGV平均能耗TQ:由各RGV运行能耗之和与服务总任务数及RGV总数量有关,表示每个RGV单个任务所消耗能耗,相同数量任务数及RGV总数的情形下,其数值越小表明其调度策略越优,计算公式为 (14) 式(14)中:P1、P2为RGV空载运行牵引功率和负载运行牵引功率。 实验工程参数:RGV水平移动速度为1 m/s;升降机垂直升降速度为0.6 m/s;升降机数量L=2; RGV数量M=3;入/出库口数量为3个且并列排布,车位总列数记为C,车库层高记为F;库位高度为2.5 m,宽度为2 m,RGV入/出库搬运时间为10 s且车辆到达进入、离开车厅总时间固定为30 s。 为研究立体车库层列组合对算法初始解的影响,对不同层、列布局(C×F)的车库模型进行仿真。考虑到车库设备安全性与结构可靠性,以及占地面积,设置车库层数所属区间[4, 8],列数所属区间[10, 26],保证库位数量保持基本一致为依据,得出如表1所示层、列不同组合。 表1 层、列不同情况组合Table 1 Different combinations of layers and columns 依据RGV服务时间最短原则,对上述9种层列组合进行仿真,图3为不同层列组合库位下的RGV平均服务时间及RGV平均利用率反映情况。 观察结果发现,当车库层数由4→8,列数由26→10变化过程中,RGV平均服务时间先减小后增大,而RGV利用率变化为先增加后减小。分析层数与列数之比发现,层与列之比约在1/10→4/10的变化过程中运行效率指标逐步向好变化,在4/10→6/10时又逐步变差,这是由于升降机位于车库巷道两端,跨层作业RGV运行至目标位置距离即为RGV待命位置距配合侧升降机位置与目标层升降机侧位置距目标位置的距离之和,显然,若将车库以列一分为二,当1/2的总列数小于总层数时,可以认为此时影响RGV作业时间的主要因素为升降机,若升降机的使用频率增加,则增加了等待升降机所用时间。以此推断,立体车库中层列比靠近1/2的层列组合方案,有利于RGV路径优化策略。 当层列组合变化为6×16时RGV平均服务时间达到最小,这是由于随着顾客到达率的增加,I/O所在层所容纳车辆数逐渐饱和,当I/O所在层车辆饱和后跨层搬运车辆一方面受升降机状态的影响,另一方面受两RGV运行路径冲突的影响,当车库列即图1中总层数x值小,列总层数y值大时,车辆在同一层的存取过程中,所受路径冲突的影响变大即此时RGV平均服务时间开始增大。 综上分析,当层数为6,列数为16时RGV最短服务时间调度模型生成的初始解效率指标最优。 图3 层列组合方案效率指标仿真Fig.3 Simulation of efficiency metrics for layer column combination scheme 顾客到达率影响RGV路径规划的复杂度,主要表现为不同到达率下RGV利用率及单个RGV单位时间内作业目标位置数量不同,导致平均服务时间不同,为了验证顾客到达率因素对所提算法影响,分别取顾客到达率λ=12,λ=20,λ=40,λ=60 veh/h情形下分两组进行实验,第一组为对照组,无路径优化策略;第二组为本文设计策略组,分析对比结果如表2所示。 根据表2可以看出,当顾客到达率λ=12、20 veh/h时,RGV平均利用率均小于50%,较无优化策略组平均服务时间分别减小8.59%、10.29%;当顾客到达率λ=40、60 veh/h时,RGV平均利用率大于50%,较无优化策略组平均服务时间减小2.92%、1.50%。高利用率下,即随着系统繁忙度增加,两组实验下RGV运行效率指标趋于相等,可以认为在RGV平均利用率小于50%的情形下本文所提RGV路径优化算法表现更优。 表2 不同到达率下RGV运行效率指标Table 2 Operational efficiency index of RGV with different arrival rates 以6×16库位布局建立矩阵地图,取3.2节中λ=12 veh/h顾客到达率水平下某时间段一台RGV位置转移过程。在该顾客到达过程仿真开始之前,设置库位状态如图4所示,黑色标记库位表示占用状态,白色标记库位表示空闲状态,RGV分配遵循就近分配原则。 根据以上库位状态信息及RGV位置信息,采用传统禁忌搜索算法与本文改进禁忌搜索算法进行实验。如图5所示为两种算法下路径长度变化曲线,可以看出,二者初始优化效果相似,但改进禁忌搜索算法收敛速度更快,且最终得到可行性路径长度更短。由此可见,改进禁忌搜索算法在更短的迭代过程下对路径分配的优化效果更佳,适合本文模型的求解。 随机抽取西安某商业立体车库2017年7月连续一周顾客泊车历史数据,在就近车位分配原则下以6层16列库位布局进行可行性验证,绘制RGV运行效率指标,如图6所示,RGV平均服务时间为101.08 s,RGV平均运行能耗为289.54 kJ。 图5 迭代过程路径长度变化曲线Fig.5 Path length change curve during iterations 图6 立体车库运行效率指标Fig.6 Operational efficiency indicators of cubic garage 可以看出,RGV服务时间及运行能耗大部分沿平均值分布且平均服务时间小于120 s,符合3.2节表2中RGV平均利用率小于50%的情形下仿真结果,说明所提路径优化算法在实际工程中有较强可行性。 本文建立了以实际车库入/出库作业过程为基础的RGV当前任务最小服务时间目标函数,提出一种带有多条件约束的RGV服务时间最短调度模型,利用改进禁忌搜索算法对RGV作业路径进行优化,仿真不同层列组合及不同到达率下RGV效率指标,得出如下主要结论。 (1)6×16层列组合库位布局下初始解效率指标趋于最优。 (2)当顾客到达率较小时,即RGV平均利用率小于50%的情形下,算法更有利于车库效率的提高。 (3)综合考虑层列组合及到达率因素,改进后算法收敛速度更快,路径搜索速度显著提升。 (4)以连续一周顾客泊车历史数据进行验证,证明了所提路径优化算法在实际工程中有较强可行性。 本研究对车库综合场景下的效率表现情况均进行了相关实验及结果分析,所提路径优化算法为提高立体车库运行效率提供参考。在本研究基础上,未来将对RGV路径冲突对策进行进一步研究。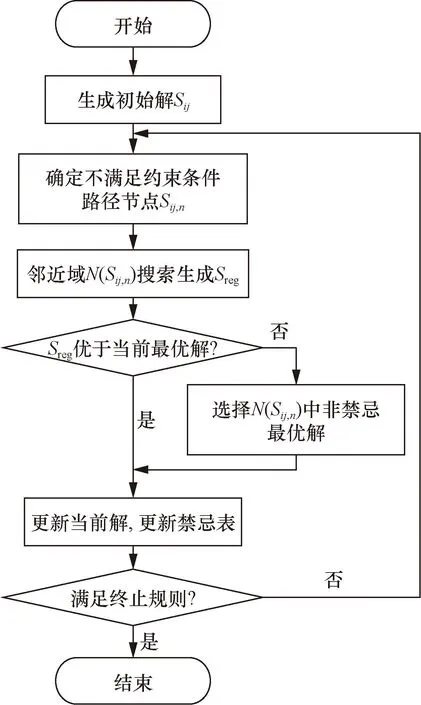
2.5 立体车库运行效率指标
3 仿真实验与分析
3.1 层、列组合影响分析
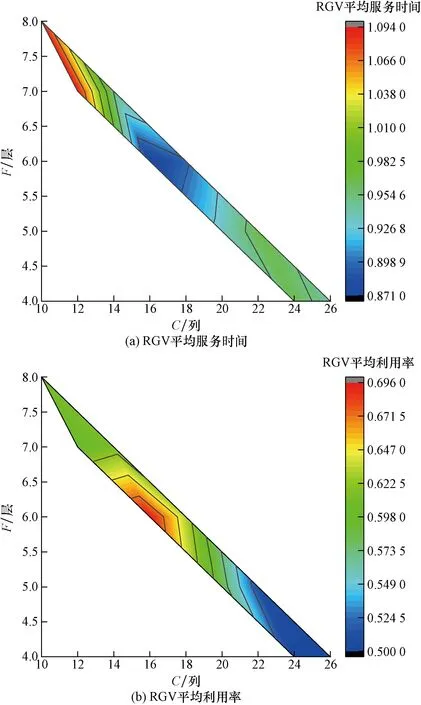
3.2 到达率影响分析
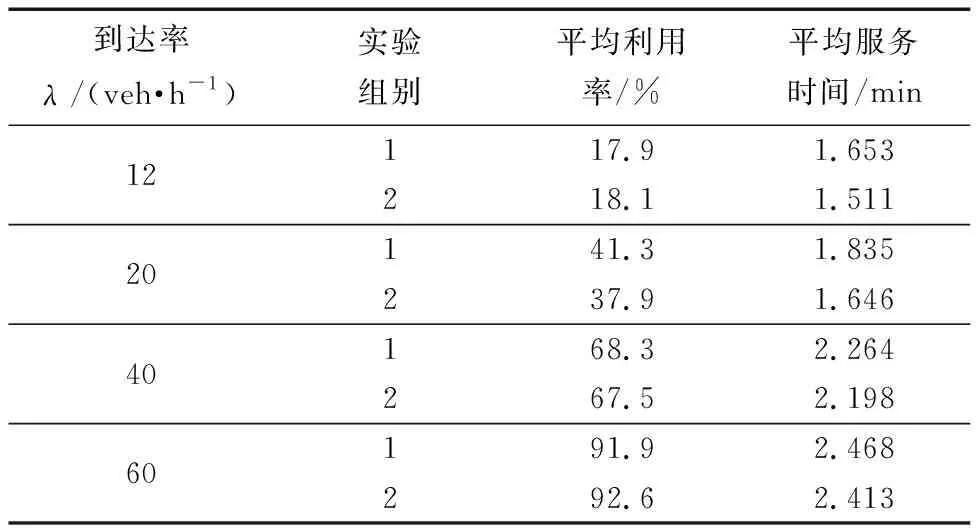
3.3 综合效率评估
3.4 实例验证
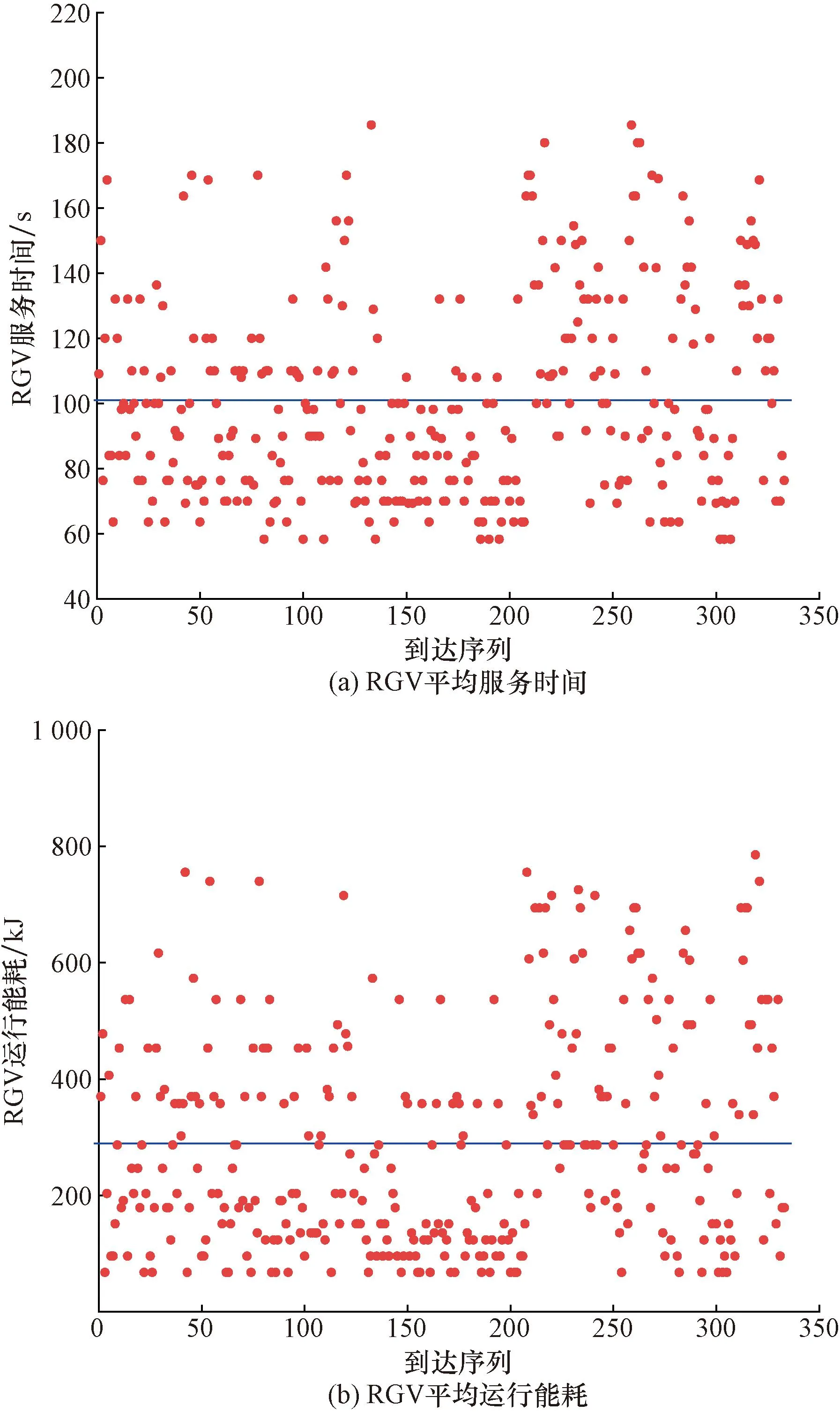
4 结论

