不同滑坡推力模式下新型变截面抗滑桩数值分析研究

曾章波,梅龙喜,裴志勇,崔茂俊

(1中国能源建设集团云南省电力设计院,云南 昆明 650500;2云南大学 建筑与规划学院,云南 昆明 650500)

0 引言

近年来,国家大力在中西部山区进行基础设施建设,须配合大量边坡工程施工,抗滑桩作为其常用的边坡支护结构,得到大量应用。由于边坡工程类型不同,其所需抗滑桩承载力不同,也对抗滑桩的截面有不同的要求。为此,不同的学者对抗滑桩展开了大量研究。颜志雄等[1-3]对实际工程中使用的圆形截面抗滑桩进行模拟,得出缩尺模型的钢筋应力、弯矩、剪力等力学特性规律和桩身裂缝分布及变形情况。其次,不同滑坡推力量值和不同推力模式均会对变截面抗滑桩的承受力产生不同的影响,但目前学者们对这方面的研究相对较少,因此缺乏相关数据和理论研究。基于这一背景,Guo Lei[4]针对变截面桩,提出了其变形计算的新方法。佴磊[5]分析了抗滑桩桩身形变、内力和钢筋混凝土桩的结构设计,并提出在不同的限制条件下,桩身内力、桩身变形的计算公式。李耀华等[6]对比分析了矩形截面桩和圆形截面桩的钢筋应力、剪力等力学性能,通过试验发现,桩身裂缝分布更均匀紧密的是后者;随着锚固段深度的增加,矩形截面桩的应力较圆形截面桩大。郑百录[7]从受力特性、工程施工、工程造价等方面分析了传统矩形抗滑桩和圆形抗滑桩的不同表现得出:矩形截面桩受力特性良好,而圆形截面桩在安全性上则更具有优势。徐展峰[8]对新型变截面抗滑桩进行了研究,采用理论、试验和数值分析相结合的方式,选取了“下圆上方”变截面抗滑桩和方形等截面抗滑桩进行对比。发现“下圆上方”型抗滑桩的桩身最大弯矩值小于方形等截面抗滑桩,且“下圆上方”型抗滑桩的结构受力更均匀。苏培东等[9]以梯形桩与矩形桩为研究对象,利用轴向受压杆件的斜截面应力计算模型,推导梯形桩桩侧土拱拱脚受压区应力状态,并分析了梯形与矩形桩侧土拱极限承载力。张泽宇[10]以模型试验为基础,研究了不同截面的双排抗滑桩。通过对矩形和等效圆形两种截面双排抗滑桩进行模拟试验和配筋计算,总结出实际建设工程中矩形与圆形的截面转化规律。秦浩锋等[11]采用了PFC2D离散元程序,构建了不同桩间净距比的抗滑桩模型,分析圆形与矩形两种典型截面,并通过离心机试验与其中一组模型进行对比,得出桩间净距比会对不同截面抗滑桩土拱效应产生不同的影响。

1 模型实验的建立

采用几何相似比系数C=10,制作某边坡支护工程的抗滑桩试验模型。模型的上部悬臂段矩形截面尺寸为100 mm×150 mm,方形截面尺寸b×h=127 mm×127 mm,下部嵌固段圆形截面直径d=180 mm。模型箱采用装配式钢板箱,其壁厚为3 mm,尺寸为1100 mm×700 mm×1500 mm。除正面可活动放置材,其余周边框架采用角钢焊接,如图1所示。

图1 模型箱设计大样正视图

模型桩采用C20混凝土制作,fc=11 N/mm2,水泥为325 MPa,二级纵向钢筋fy=310 N/mm2,桩长1.15 m,制成方形、矩形、下圆上方和下圆上矩四种截面形式的抗滑桩。混凝土保护层取10 mm,截面为HPB235φ8 mm的钢筋,截面采用对称配筋As=151 mm2(3φ8),箍筋为铁丝,间矩15 cm,由钢丝作为绑筋,贴好钢筋应变片之后支模浇筑混凝土。待模型合格后对模型桩表面贴片部位处理并贴片,并安装在指定位置,与之同时进行土层回填和仪器安装。

2 变截面抗滑桩数值分析

2.1 模型试验有限元模型的建立

2.1.1 本构模型及数值模型相关参数选取

考虑使用材料和计算收敛性对本构模型的影响[12-16]。在填土时,遵照摩尔-库伦准则,在模型实验时,遵照线弹性模型;在数值分析时,采用实体单元模拟了锚固土层和抗滑桩,其次,还使用了印刻法将钢筋刻在抗滑桩内,并以梁单元模拟钢筋。抗滑桩的相关参数已在上文阐述,土层的力学指标则是通过土工试验获得,具体参数见表1。

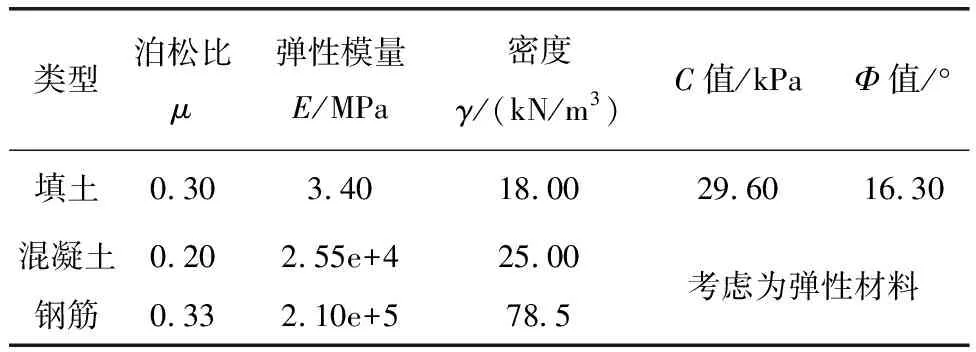
表1 数值模型输入参数表

2.1.2 数值模型计算单元及网格划分

通常实体单元和混合网格生成器可以结合使用,将混凝土和土层进行单元分割,以观察其数值变化。因此本文运用上述工具进行了模型试验,混凝土、土层单元分割尺寸分别为10 mm、100 mm,其接触点范围为10～100 mm。本文印刻在抗滑桩内的钢筋单元分割尺寸为10 mm。数值模型以室内模型试验为原型,建立了4组不同截面的模型。其中X轴表示宽度,Y轴表示长度,Z轴表示高度,同时对模型进行了网格的划分。由于4种截面方法相似,本文仅展示了方形截面,如图2所示。

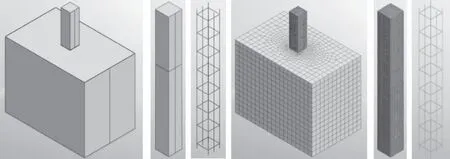
图2 方型截面抗滑桩(含钢筋)数值分析模型及网络划分示意图

2.2 计算结果分析

对数值分析模型经过有限元计算后,得出了方形、矩形、下圆上方和下圆上矩四种不同截面的抗滑桩在三种滑坡推力作用下的计算结果,通过有限元软件提取了各组数值模型的Mise应力云图,并进行直观的分析。

2.2.1 表面及钢筋应力数值结果分析

1)下圆上方形截面抗滑桩

图3为表面应力的结果提取云图及曲线图。通过提取不同荷载作用下的Mise应力云图,发现选取任一荷载作用下的云图均能代表应力变化的规律,因此本文仅选择了6.3 kN矩形荷载、三角形荷载和梯形荷载的应力云图,下文处理亦然。

图3 下圆上方截面抗滑桩应力云图及曲线图

由图3可得如下规律,一是下圆上方截面的桩身应力存在两个较高点,在这两点处均呈现了应力先上升、然后到达该点后又呈下降的趋势(图3(d))。可以看出,应力在变截面处发生了突变现象,应力最大值出现在变截面以上0.01 m处。从图3(e)中的矩形荷载方形边线曲线中得到变截面的圆形部分再次减小,方形部分变化程度在减小。二是桩身应力值在-0.60 m处呈上升趋势,这一趋势持续至-0.70 m。三是抗滑桩的应力值大小依次为矩形荷载、梯形荷载、三角形荷载。

图4为钢筋应力的结果提取云图。可以看出,下圆上方截面在桩身坐标0处也发生了突变,但值得注意的是只在桩身0.01 m处存在一个较高点。尽管在桩身-0.2 m处有凸起,但其应力值与-0.01～0.20 m段的差距不大,因此不能视为较高点。此外,对比发现,钢筋应力变化从桩身0.20 m直至-0.01 m幅度较小。这说明在-0.01～0.20 m范围内受力更加均匀。

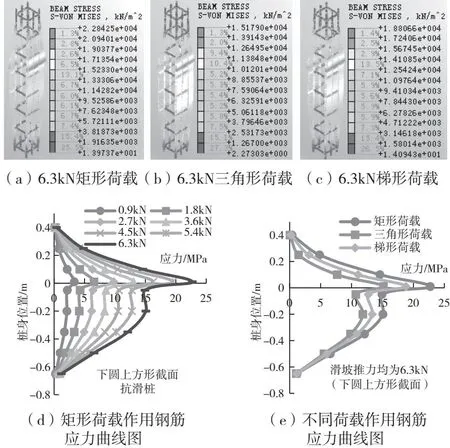
图4 下圆上方形截面抗滑桩钢筋应力云图及曲线图

2)下圆上矩形截面抗滑桩

由于表面应力云图与下圆上方形截面类似,故此处不再展示。图5为表面应力结果曲线图,可以看出,虽然其应力数值与下圆上方形截面不同,但应力变化规律是一样的。

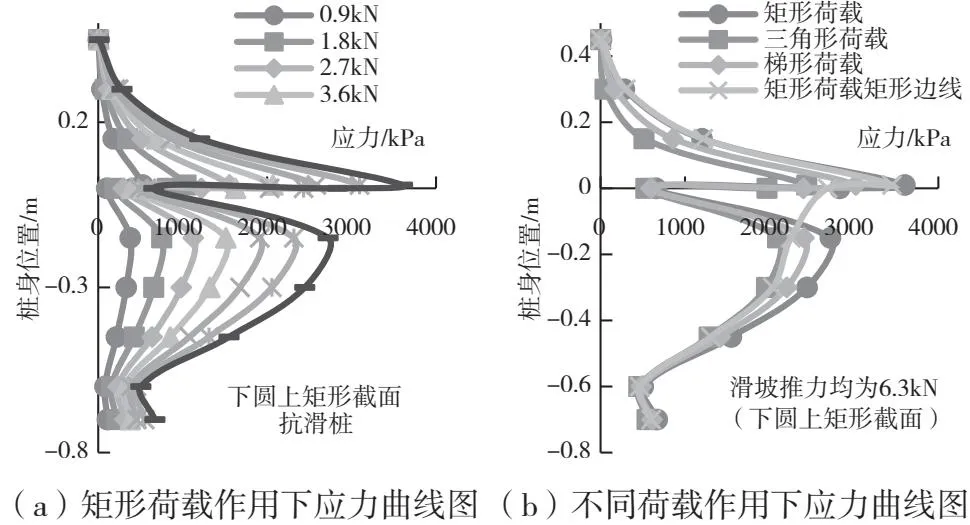
图5 下圆上矩截面抗滑桩应力曲线图

同理,钢筋应力云图也不再展示,仅展示钢筋应力结果曲线(图6)。可以看出,相较于下圆上方截面其在变截面处的突变程度要大很多,即下圆上矩形整体受力不如下圆上方均匀。其余规律与下圆上方截面的规律一致。

图6 下圆上矩截面抗滑桩钢筋应力曲线图

3)方形截面抗滑桩

图7为表面应力结果提取云图及曲线图,可以得出如下有关方形截面的结论:一是不同荷载作用下,其表面应变与荷载呈正相关。二是同级荷载作用下的表面应力数值,由桩底至桩顶数据逐渐变小。三是自0.4 m开始呈上升趋势,于桩身-0.15 m处达到较高点,随后下降直至-0.60 m处又呈上升趋势,其中自-0.60 m处呈上升趋势持续至-0.70 m,其原因也是受到了土体压力的影响。四是较之其他部位,在桩身-0.15 m较高点附近的应力值随荷载增加的幅度更大。五是方形截面抗滑桩的应力数值高低依次为:矩形荷载、梯形荷载、三角形荷载。此外,由钢筋应力数据分析可知,其与表面应力变化规律相似,故不再分析。

图7 方形截面抗滑桩表面应力云图及曲线图

4)矩形截面抗滑桩

由矩形截面抗滑桩的表面和钢筋应力结果发现,除数值稍有差异外,其规律与方形截面的相似,故此处不再分析。

2.2.2 同种荷载作用下不同截面抗滑桩表面及钢筋应力分析

为进一步发现不同截面抗滑桩的表面和钢筋应力的差异,本文选取了同为6.3 kN的荷载大小以分析四种截面的相关应力变化规律。值得注意的是,分析发现下圆上方形在桩身0.0 m处应力出现较大的突变,分析其原因为0.0 m处的取值为中心轴对称处的数据,而由图5可知方形边线中心轴对称处的应力大于0.0 m处的,因此本文去除了0.0 m处的突变值,得到了更为合理的桩身应力的变化情况,如图8所示。

图8 不同截面抗滑桩应力曲线拟合图

由图8和图9可得出结论,等截面抗滑桩的钢筋应力值大于变截面抗滑桩的,且下圆上方形大于下圆上矩形的,进而在可选择抗滑桩截面时,首选下圆上矩形截面,其次选下圆上方形,再次选矩形,最后才选方形。

图9 不同截面抗滑桩内部钢筋应力曲线图

2.2.3 桩周土压力数值结果分析

本文利用X-Z平面将填土层切开用于分析桩前后的土压力变化情况。首先,由于同种截面在不同滑坡推力模式下,任选一种荷载作用下,其变化均能代表变化规律,故本文选取了矩形荷载进行分析。其次,本文选取了同为滑坡推力6.3 kN,不同的荷载形式的土压力之间的差异。最后选取了同一荷载作用,不同截面的土压力变化差异。

1)下圆上方截面抗滑桩

图10为下圆上方截面抗滑桩周土压力云图。由于选取任一级别荷载作用有限元结果,其变化规律均能代表桩周土压力变化,因此本文只选取了滑坡推力为6.3 kN,矩形、三角形和梯形荷载作用下的土压力云图。

图10 下圆上方形截面抗滑桩周边土压力云图

将数值分析获取的数据绘制成如图11、图12的桩周土压力曲线图。重点观察桩前自0.0 m处土压力下降直至-0.5 m处,桩后自-0.7 m土压力开始上升直至-0.5 m处。在荷载大小相同时,桩周土压力大小依次为矩形荷载、梯形荷载、三角形荷载。由数据结果云图及相关曲线发现四种截面抗滑桩的土压力数值不同,但变化规律类似。

图11 矩形荷载作用下桩周土压力曲线图

2)不同截面抗滑桩周土压力对比分析

根据数值模拟的数据绘制在同种荷载下不同截面的土压力变化情况(图13)。可以看出,三种荷载作用下不同截面的桩周土压差异:等截面抗滑桩均大于变截面的;若进一步比较数值,下圆上方和下圆上矩基本相同,方形桩周土压力略大于矩形的。

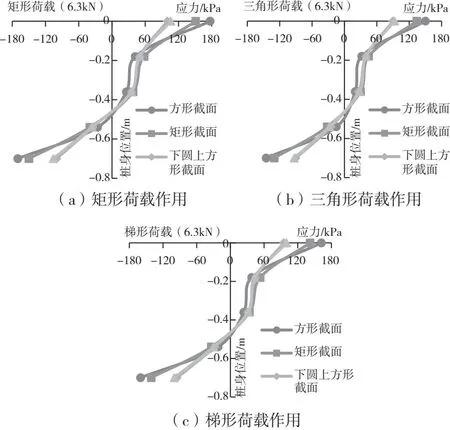
图13 不同截面抗滑桩周土压力曲线图

2.2.4 桩体位移数值结果与分析

1)下圆上方形截面抗滑桩

通过分析有限元结果发现,无论任选一种荷载形式还是任选一种截面,其桩体位移变化均可以代表其他的。因此本文选取推力6.3 kN,荷载形式为矩形、三角形和梯形,截面为下圆上方变截面,绘制了其桩体位移云图及曲线图,见图14。

图14 下圆上方形截面抗滑桩位移云图及曲线图

由图14可知,4种截面抗滑桩的位移与荷载呈正相关,近乎为线性相关。此外,抗滑桩基本绕桩身-0.45 m处转动,说明4种截面抗滑桩均为刚性桩,不同荷载对位移的作用从大到小依次为:矩形荷载、梯形荷载、三角形荷载。

2)不同截面抗滑桩位移比较分析

图15为进一步比较不同截面的位移变化曲线图。可以得出在同种荷载作用下位移大小依次为:矩形截面、两种变截面并列、方形截面。

图15 不同截面抗滑桩位移比较曲线图

3 结论

(1)等截面和变截面抗滑桩的表面及钢筋拉压

应变与荷载呈正相关。不同截面抗滑桩的应变大小均依次为矩形荷载作用、梯形荷载作用、三角形荷载作用。

(2)等截面抗滑桩的表面及钢筋拉压应变的变化规律相似,同级荷载作用下自桩底至桩顶应变逐渐减小,峰值出现在桩身-0.15 m处,随后逐渐增大。变截面抗滑桩表面拉压应变规律为:同级荷载作用下桩身应力存在两个峰值点,其最大点出现在变截面以上0.01 m处;桩身-0.60～-0.70 m段应力值逐渐增大,其原因为该段桩后受到了土压力反压,桩前的桩底承受了土体向上的压力。变截面抗滑桩钢筋拉压应变的变化规律为:同级荷载作用下,变截面处出现峰值,在桩身-0.01～0.20 m段的应力变化幅度较小,桩身在该段受力比较均匀。

(3)桩周土压力数据分析表明,4种截面抗滑桩土压力均与荷载呈正相关;在同等荷载下,桩周土压力为矩形荷载大于梯形荷载大于三角形荷载;在同等荷载大小和荷载形式作用下,桩周土压力最大的是矩形截面,其次为方形和下圆上方形截面,最小的是下圆上矩形截面,但四者数值差距不大,变化幅度均小于10%。

(4)相同荷载作用下,位移最大的是矩形截面,最小的是方形截面,下圆上方截面和下圆上矩截面居中且其变化值基本相同,说明变截面位移控制比矩形截面的好。在可选择抗滑桩截面时,首选下圆上矩形截面,其次选下圆上方形,再次选矩形,最后才选方形。