基于支持向量机的斜拉桥应力可靠度分析

董 曦

(湖南省交通运输厅规划与项目办公室，湖南 长沙 410029)

0 引言

斜拉桥因其造型美观、跨越能力大以及梁体截面尺寸小等特点，近些年来得到了广泛的应用[1-2]。由于斜拉桥往往是区域交通网络中的控制性工程，是地区经济社会的生命线，一旦发生事故，对人民生命安全和地区经济发展均影响巨大。因此，为确保斜拉桥的安全运营，对其可靠度进行研究具有十分重要的意义。

目前，国内外相关研究人员对斜拉桥的可靠度进行了众多研究[3-4]。王涛等[5]采用有限元软件建立了某大跨度铁路斜拉桥的有限元模型，基于损伤理论，采用蒙特卡洛法对该桥在风以及列车动力作用下的可靠度进行了分析；鲁乃唯等[6]根据斜拉桥的结构失效特点建立相应模型，基于神经网络和联合智能算法对某斜拉桥的体系可靠度进行了分析，并探讨了相关参数对结构体系可靠度的影响；刘剑等[7]采用ANSYS建立了某斜拉桥的有限元模型，采用综合分析法对该大跨度斜拉桥的可靠度进行了分析。然而，上述方法有一定的运用环境和限制条件，其中采用蒙特卡洛法需要抽取大量的样本，才能满足精度要求，运算量较大，耗时久；神经网络法在泛化时，易出现对数据进行过拟合的现象，从而影响可靠度计算。

基于此，本文阐述了支持向量机的基本原理，提出了基于支持向量机的桥梁结构可靠度分析方法。以国内某斜拉桥为工程实例，建立了该桥斜拉索应力极限状态方程以及主塔应力极限状态方程，通过基于支持向量机的桥梁可靠度计算方法，得到了斜拉索的应力可靠度以及主塔应力可靠度。

1 基本理论

1.1 支持向量机基本原理

支持向量机(SVM)是一种基于统计学习原理的机器学习算法，其基本原理为超平面上的样本数据线性分类器，可用于处理数据的拟合和预测，且支持向量机可以根据数据样本针对性地改进核函数参数的选择，对于不同类型的数据均有较好的学习性和适应性，对于结构近似功能函数的拟合具有天然的优势[8]。

SVM算法可根据线性可分的假定进行相应的推导，本文通过二维线性回归对其基本原理进行相应阐述，其中回归是指将已得到的样本数据点与响应值进行拟合，再根据拟合得到的拟合函数预测位置样本数据点的响应值，二维线性分类如图1所示，其中矩形点和三角形点分别表示两类不同的训练样本，H为将两类训练样本分隔开来的分类线，H1、H2分别为距离分类线最近并且通过各自训练样本点的线，同时该线平行于分类线H，h为H1与H2之间的距离，称为分类间隔。当分类间隔最大并且使两类训练样本误差率为0的分类线H称为最优分类线，若将其扩展至三维空间，最优分类线即可称为最优超平面。

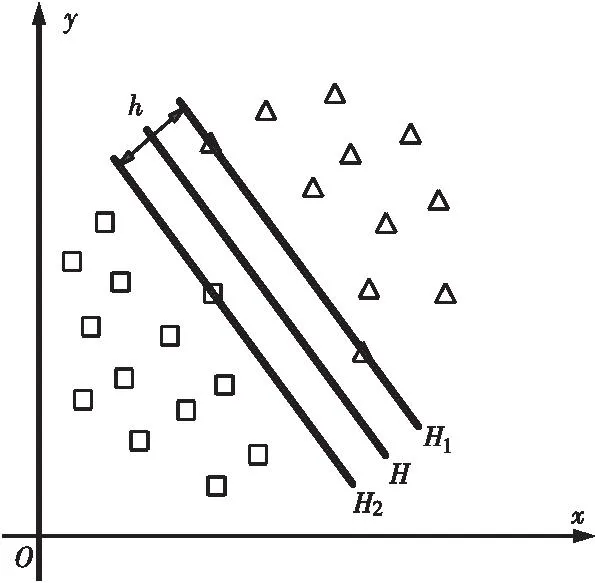
图1 二维线性分类示意

假设存在两类线性可分的训练样本{(x1，y1)，(x2，y2)，……，(xn，yn)}，其中xn∈Rn，xn∈(-1，1)，定义其判别函数如式(1)所示：

y(x)=αx+b

(1)

那么，分类面方程可表示为：

αx+b=0

(2)

将训练样本进行归一化处理，使两类训练样本均满足|y(x)|≥1,即:

yi(αxi+b)≥1,i=1,2,…,n

(3)

通过式(3)即可将两类训练样本正确分隔开，此时分隔间隔h=2/α。为得到最优超平面，分裂间隔h应尽可能大，即α2应取最小值。因此，可将上述问题转化为约束优化问题，如式(4)所示：

(4)

式中：minα2表示目标函数，yi(αxi+b)≥1表示分类超平面。若H为最优超平面，那么处于分H1、H2上的训练样本即为支持向量。

引入拉格朗日函数可将其转化为二次规划寻优的对偶问题，其中定义拉格朗日函数如式(5)所示：

(5)

式中：vi表示拉格朗日乘子，通常情况下vi=0，但若训练样本为支持向量时vi≠0。

令上式对α、b、v的偏微分为0，则可求得拉格朗日函数的最小值。根据二次规划寻优的对偶问题可得：

(6)

对于式(6)，可将其视为函数求极值问题，通过计算推导可得其最优分类函数：

(7)

上述为线性可分情形下采用支持向量机的求解方法，然而在实际应用中非线性可分的情形居多。对于非线性可分的情形，可在线性可分的基础上引入松弛系数ξ求解[9]，即将式(4)转化为式(8)：

(8)

式中：c表示惩罚因子，主要用于减小计算过程中的误差；松弛系数ξi≥0。

1.2 样本的选取

采用支持向量机法对功能函数进行模拟时，通常需要一定数量的训练样本，本文利用拉丁超立方抽样的方法对数据进行抽样，该方法的优点是其具有记忆功能，以使抽样得到的训练样本覆盖较大的范围，从而使样本点分布均匀，避免样本点出现局部集中的情况[10]。对于本文选用的斜拉桥，取训练样本区间为[μ-3δ，μ+3δ]，其中，μ表示随机变量的均值，δ表示随机变量的标准差，此区间已包含绝大部分样本点。

2 可靠度分析方法

桥梁的可靠度是指桥梁结构在规定的条件下、规定的时间内完成预定功能的能力[11]。在实际工程中，可靠度通常用于预测和评估结构的性能，通常可采用功能函数来表示结构的具体状态，如式(9)所示：

Z=g(R,S)=R-S

(9)

式中：R表示结构抗力；S表示荷载效应。

影响结构可靠度大小的因素有很多，例如材料性能、荷载分布情况以及服役环境等，考虑到影响结构可靠度因素的不确定性，可将功能函数式(9)改写为：

Z=g(X)=g(X1,X2,…,Xm)

(10)

式中：X1，X2，…，Xm表示影响结构可靠度的随机变量。

桥梁结构的可靠性概率可以通过式(11)计算得到：

Pr=P(Z>0)=

(11)

通过式(11)直接计算得到结构的可靠性概率十分困难，因此，在计算分析中，通常使用结构的可靠度指标β来代替可靠性概率Pr，它表示结构安全性的度量，可靠度指标β的计算表达式如(12)所示：

(12)

式中：μz、σz分别为功能函数Z的均值和方差，假定功能函数Z服从正态分布。

对式(12)进一步细化可得：

(13)

3 算例分析

3.1 工程概况

本文选取国内某斜拉桥为工程实例，桥梁全长为640 m，跨径组合为(50+95+350+95+50)m，主梁采用预应力混凝土箱梁，C55混凝土；主塔为独柱式桥塔，采用C50混凝土；斜拉索采用聚乙烯高强钢丝拉索。该斜拉桥总体布置如图2所示。

图2 算例斜拉桥总体布置(单位：m)

3.2 有限元模型建立

本文采用有限元软件ANSYS对该斜拉桥进行建模，其中主梁采用BEAM44单元进行模拟，桥塔采用BEAM188单元进行模拟，采用LINK10单元对斜拉索进行模拟，其垂度效应采用ERNST公式进行计算，桥面板采用SHELL63单元进行模拟。

3.3 随机变量的选取

桥梁结构实际建设是一个理论与实际相融合的过程，相关设计人员提供的构件几何尺寸、材料特性等均是在理想条件下设计的。然而，在桥梁的施工过程中，由于施工工艺以及施工技术人员施工水平的差异会导致结构实际所处的状况与理想设计时的状态有所差异。因此，为了定量分析上述差异对桥梁结构的影响，首先需要选取影响斜拉桥可靠度的随机变量。斜拉桥结构复杂，影响因素较多，为了简化计算，本文算例斜拉桥考虑的随机变量主要包括：主梁、主塔以及斜拉索的弹性模量和容重、二期恒载、汽车荷载等。参考相关文献[12]以及相关规范标准[13-14]，本文选取的随机变量取值如表1所示。

表1 随机变量相关参数取值随机变量主梁弹性模量/GPa主塔弹性模量/GPa斜拉索弹性模量/GPa主梁容重/(kN·m-3)主塔容重/(kN·m-3)斜拉索容重/(kN·m-3)汽车荷载/(kN·m-1)二期荷载/(kN·m-1)分布类型正态分布正态分布正态分布正态分布正态分布正态分布极值I型分布正态分布均值35.534.5204262578.532.96112.28变异系数0.10.10.10.10.10.10.120.08

3.4 建立功能函数

3.4.1斜拉索应力失效模式的功能函数建立

由相关规范[14]可知，在正常运营状态下，斜拉索应力的应满足式(13)：

[σ]≤fyk

(13)

式中：[σ]表示斜拉索容许预应力；fyk表示斜拉索屈服强度。

由此可建立斜拉索应力失效的功能函数，如式(14)所示：

Z1=[σ]-σ(E1,E2,E3,γ1,γ2,γ3,q1,q2)

(14)

式中：E1、E2、E3分别为斜拉桥主梁、主塔以及斜拉索的弹性模量；γ1、γ2、γ3分别为斜拉桥主梁、主塔以及斜拉索的容重；q1、q2分别为汽车荷载和二期荷载。

3.4.2主塔应力失效模式的功能函数建立

算例斜拉桥为超静定结构，其主塔为最主要的偏心受压构件，承担着由主梁传递过来的恒载以及活载作用。由于主塔采用的是C50混凝土，故其轴心抗压强度设计值[σ]=23.1 MPa，从而可得到主塔应力失效模式的功能函数为：

Z2=[σ]-σ(E1,E2,E3,γ1,γ2,γ3,q1,q2)

(15)

3.5 可靠度计算

3.5.1斜拉索应力可靠度计算

采用拉丁超立方抽样的方法选取200组数据，其中20组为测试样本，其余为训练样本，各随机变量取值范围为[μ-3δ，μ+3δ]，通过内插法对各随机变量进行相应计算可得训练样本。然后，对训练样本进行归一化处理，在通过支持向量机对其进行学习并拟合功能函数，并从中选择最优结果。最后，根据式(12)可计算得到斜拉索的应力可靠度，如图3所示。由于算例斜拉桥为对称结构，故图3中仅列出了半结构的斜拉索应力可靠度，其中边墩到索塔的斜拉索编号依次为1#～14#，索塔至跨中的斜拉索编号以此为15#～28#。

图3 各斜拉索可靠度

从图3中可以看出，斜拉索可靠度指标整体上符合越靠近主塔，可靠度指标越大的规律，其中可靠度指标最大的斜拉索为15#，最大值达到了7.30；可靠度指标最小的斜拉索为边跨最外边拉索，即1#斜拉索，其值为4.21。根据设计可知，该桥斜拉索规格并不完全一致，共有6种规格，由于离主塔较远的斜拉索可靠度较小，因此，在斜拉索设计过程中，可通过调整斜拉索的规格以使全桥各斜拉索的可靠度分布均匀，从而提高斜拉索的体系可靠度。

3.5.2主塔应力可靠度计算

该桥主塔应力可靠度的计算与3.4.1节类似，故不再赘述。为了分析该斜拉桥主塔各个位置可靠度指标的变化规律，将3#主塔分为24个单元，从3#主塔底部至顶部依次进行编号为1#～24#，其中，5#单元为主塔与主梁相接位置的上部，4#单元为主塔与主梁相接位置的下部，主塔各单元的可靠度如图4所示。

图4 斜拉桥主塔各单元的可靠指标

从图4中可以看出，5#单元的可靠度最小，为4.56，表明其所处位置(即主塔与主梁相接位置上部)的主塔压应力最大；主塔与主梁相接位置的下部各单元的可靠度均较大，其中最大值达到了7.50；而主塔与主梁相接位置上部的可靠度度呈现递增趋势，即距离主塔与主梁相接位置越远，其单元可靠度越大，其中24#单元的可靠度达到了7.05，主塔底部与顶部位置的可靠度均较大。

4 结论

本文阐述了支持向量机的基本原理，基于可靠度理论，得到了基于支持向量机的桥梁可靠度分析方法。以国内某斜拉桥为工程实例，建立了该桥斜拉索应力极限状态方程以及主塔应力极限状态方程，通过基于支持向量机的桥梁可靠度计算方法，得到了斜拉索的应力可靠度以及主塔应力可靠度及以下结论：

1)越靠近斜拉桥的主塔，斜拉索的应力可靠度越大，其中最大值达到了7.30，最小值为4.21。在实际工程中，可通过调整斜拉索的规格使全桥各斜拉索的可靠度分布均匀，从而提高斜拉索的体系可靠度。

2)主塔与主梁相接位置上部的可靠度呈现递增趋势，距离主塔与主梁相接位置越远，主塔单元的可靠度越大。

3)主塔应力可靠度最小值出现在主塔与主梁相接位置上部第1个单元，表明此处主塔压应力最大，主塔与主梁相接位置下部各单元的可靠度均较大。