大数据背景下基于PCA-DELM 的入侵检测研究

王振东，王思如，王俊岭，李大海

（江西理工大学 信息工程学院，江西 赣州 341000）

0 引言

随着互联网的普及和计算机技术的更新发展，网络中产生的数据规模愈发庞大，其中存在着大量的网络攻击行为威胁互联网环境和网络安全。再加之5G、云计算和物联网等技术的广泛应用，数据在互联网中的传输速度极大提高，大数据时代来临，其集中化、高透明、大规模的特征为信息安全维护带来了巨大挑战。因此，大数据背景下的网络信息安全是目前各界聚焦的关键难题。为应对上述问题，防火墙作为一种安全设备被广泛应用，通过管理员们所制定的安全规则防止某些数据流的传播，提高了接收数据流的准确性。然而，仅凭借防火墙自身无法辨别出正常数据流和异常数据流，入侵检测（Intrusion Detection，ID）作为具有主动防御能力并能动态检测入侵行为的一种新型安全机制，已逐渐成为大数据时代下网络安全的关键技术。传统入侵检测方法对检测效率、检测规模、检测体系结构等存在某些限制，而智能入侵检测技术应用模糊信息识别、规则产生式专家系统、数据挖掘、机器学习及深度学习等技术，极大提高了入侵检测率和检测速度，最大可能地防御病毒入侵。

当前，入侵检测技术相关研究大多聚焦在以下3 个方面：①基于数据挖掘的入侵检测，如王意洁等［1］基于同一网络威胁行为的预警间存在特定关系这一思想，应用数据挖掘算法寻找隐匿在数据分布背后的关系，并依据所发现的关联信息数据对威胁行为序列进行重构；②基于机器学习的入侵检测，Martins 等［2］提出对抗性机器学习方法被应用于入侵及恶意软件检测场景中，实验结果表明，该方法在恶意软件及入侵检测中有效；③基于神经网络的入侵检测，Yang 等［3］将改进的卷积神经网络（Convolutional Neural Networks，CNN）算法应用于无线网络模型，并进行相应的入侵检测，该算法优化的模型与其他机器学习算法相比，在执行效率和分类准确率等指标上均有良好效果，相比于传统入侵检测分类模型有明显提升。Yang 等［4］针对物联网安全问题，结合LM 算法优化速度快、鲁棒性强的特点，提出LM-BP 神经网络模型，并将其应用于入侵检测系统，该模型通过LM 算法对传统BP 神经网络的权值阈值进行优化，再利用BP 算法对数据集进行分类，具有更高的检测率和更低的虚警率，但学习速率较低。Wang 等［5］利用深度卷积神经网络（CNN）学习网络数据流量的低层空间特征，然后利用LSTM 网络学习高层时间特征，设计出一种新型网络入侵检测模型HAST-IDS，该模型通过多组基准测试，其结果表明HAST-IDS 在准确率、检测率等方面均优于其他已有方法，提高了入侵检测实时性。

深度学习是神经网络的进一步发展，也是对人工智能技术的加强，它通过模仿人脑机制分析处理数据，利用深度神经网络，将模型处理得更为复杂，从而使模型对数据的理解更加深入，例如图像、声音和文本［6］。深度学习已经在控制领域［7］、自然语言处理［8］、情感分析［9］等领域取得成效，这些成果也证明了深度学习是具有实用性的分类识别工具。在入侵检测领域，Khan 等［10］提出两阶段深度学习模型，第一阶段将网络流量分为正常和异常两类，第二阶段将第一阶段得到的特征状态作为检测的附加特征，该模型的优点在于从无标记的网络数据中提取有用的特征表示。Su 等［11］在注意力机制与双向长短期记忆（BLSTM）的前提下，设计了交通异常检测模型BAT，该模型可快速有效地提高异常检测能力。Lee 等［12］开发了基于事件分析的人工智能系统，用于处理数据并更好地运用不同的人工神经网络方法。

综上，虽然上述模型在入侵检测过程中展现出优越的性能，但在大数据时代下，数据流量的高速传输和庞大规模这两个特性要求入侵检测模型必须具有良好的实时性，若不能及时处理高速传输的网络流量，模型将出现严重时滞现象，无法抵御实时网络的安全威胁。因此，上述模型还存在以下问题：①两阶段深度学习模型中第一阶段在面对海量的网络数据时会大幅增加时间成本；②仅在一个数据集上的测试结果不能展现模型的泛化性和可移植性；③模型评价指标系统单一，没有其他评价指标进行交叉分析，不够全面。对此，本文在大数据背景下提出了一种轻量级神经网络的入侵检测模型（PCA-DELM），模型首先使用主成分分析方法（Principal Component Analysis，PCA）对含有正常或攻击的网络数据进行降维处理，这在庞大的数据集上能大幅减少时间成本，加快分类速率。鉴于极限学习机优秀的表征能力，将其引入到入侵检测领域，结合自动编码器（Auto Encoder，AE）对数据进行监督分类，再在UNSW-NB15 数据集上进行二分类和多分类实验，测试其入侵检测性能并验证模型可移植性，最后在实时网络流量CIDDS-001 数据集上模仿验证该模型在实际复杂的网络中对入侵行为的检测能力。以上实验均通过多个评价指标交叉分析本文分类模型与传统分类算法、经典机器学习分类器分类结果，实验结果表明，本文所提出的智能入侵检测方法在准确率、精确率、真正率等指标上有显著提高。

1 深度极限学习机

1.1 极限学习机

极限学习机（Extreme Learning Machine，ELM）［13］是一种针对于单隐层前馈神经网络（Single-hidden Layer Feedforward Neural Network，SLFN）［14］的机器学习算法。与传统的SLFN 算法不同，ELM 可随机选择输入层权重和隐藏层偏置，输出层权重通过最小化由训练误差项和输出层权重范数的正则项构成的损失函数，依据Moore-Penrose 广义逆矩阵理论计算求出［15］。相比于传统神经网络需人工设置大量参数，极限学习机训练参数更少、学习速度更快、泛化能力更强。

给定有N个标记样本数据的训练集，k(xi，ti)，xi=[xi1，…，xin]T∈Rn表示第i个样本示例，ti=[ti1，…，tim]T∈Rm是每个样本示例所对应的标签，n表示训练数据集的特征个数，m表示训练数据集的类别个数。若样本xj对应第k类，则将标签xj的第k个值设定为1，剩余(m-1)个值设成-1。如图1所示，ELM 的网络结构和单隐层前馈神经网络相似。

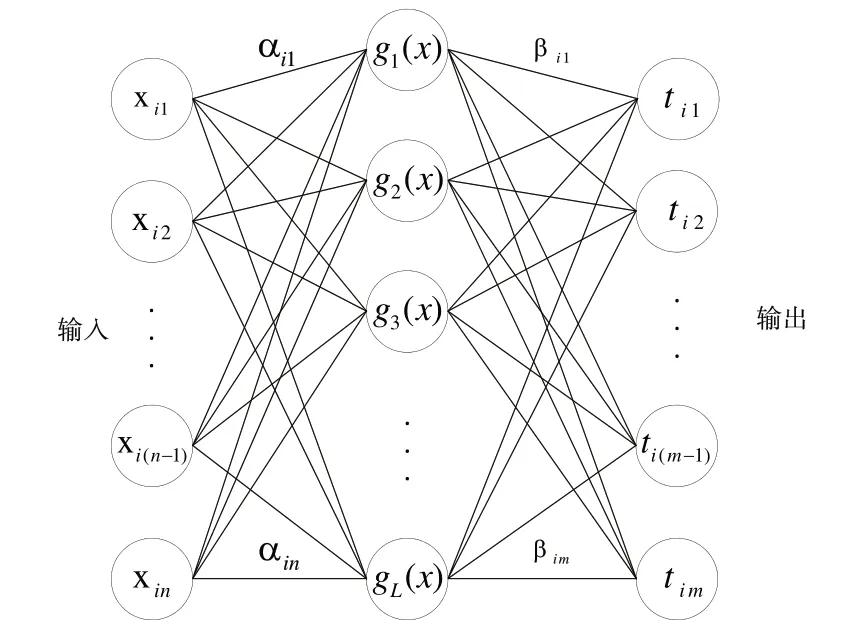
Fig.1 ELM network structure图1 ELM网络结构

包含L个隐藏节点的ELM 表示如下：

βi=[βi1，βi2，…，βi m]T是整个输出层的权重系数，βi1代表g1(x) 和ti1两个神经元之间的权重系数，αi=[αi1，αi2，…，αi m]T是连接输入层和第i个隐含层的输入权重，bi是第i个隐藏层的偏置，G(αi，bi，xj)是第i个隐藏层的输出矩阵。若第i个隐藏层的激活函数为g(x)，则隐藏层的输出为：

式（1）用矩阵形式表示为：

为达到输出数据的期望值，训练网络后需得出参数最优值，使：

深度极限学习机最终是要最小化实际输出和期望输出间的误差，也即最小化损失函数：

ELM 算法中参数(αi，bi)是随机生成，因此也唯一确定。其解决方法可以转化为：

根据文献［16］可知，要求解的范数最小且唯一。为提高模型泛化能力，加入了正则项，求解问题则转化为：

其中，λ是正则化系数，其解如下：

其中，I是单位矩阵。

1.2 基于ELM的表征学习

1.2.1 基于极限学习机的自编码器

自动编码器（Auto Encoder，AE）是一种无监督神经网络模型，它利用输入X自身作为监督，通过训练神经网络模型期望得到一个重构输出X'。因此AE 无需标记训练数据。在ELM 中引入AE 的思想，使ELM 的输入也被视为目标输出，即输出Y=X，引入自编码器的极限学习机ELMAE（Extreme Learning Machineasan Auto Encoder）的网络结构如图2所示。

Fig.2 ELM-AE network structure图2 ELM-AE网络结构

简言之，ELM-AE 类似于一个逼近器，其目标是尽可能让网络的输出与输入相同，同时使隐藏层的输入参数(αi，bi)随机生成后正交。其优势如下：

（1）可将输入数据映射到不同或等维度的空间，实现维度压缩、稀疏表达或等维度的特征表达。

（2）可清除特征之外的噪声，使特征之间分布更为均匀和线性独立，提高系统泛化性。

ELM-AE 的输出可由式（1）转化为式（9）求出。

其中，α是由αi构成的矩阵，b是由bi构成的向量。

针对维度压缩和稀疏表达，隐藏层的输出权重β可由式（8）转化为式（10）求出。

其中，X=[x1，…，xN]是输入数据。

针对同维度的特征映射，权重β可由式（11）计算求出。

由文献［16］可知，βT β=I。

1.2.2 深度极限学习机

基于ELM-AE 的3 种不同的特征表达功能，可以将其作为深度极限学习机（Deep Extreme Learning Machine，DELM）的基础模块。与传统深度学习算法相同，DELM 应用逐层贪婪的方式训练网络，DELM 每个隐藏层的输入权重都用ELM-AE 初始化，执行分层无监督训练。与传统深度学习算法相比，DELM 没有反向微调的步骤。

DELM 的目的是使输出信息无限逼近原输入信息，其基本思想是通过对每一层的训练，最大程度地减小重构误差，最终得到输入信息的高级特性。DELM 模型的主要训练步骤则是将原始输入信息样本X视为下一个ELM-AE的目标输出(X1=X)，从而得到输出权值β1。然后，将DELM 的第一个隐藏层的目标输出矩阵H1，当作下一个ELM-AE 的输入和目标输出(X2=H1)，依次逐步地展开训练，最后一层用ELM 训练，可以使用式（6）求解DELM 的最后一个隐藏的输出矩阵βi+1。DELM 每一层隐藏层的输入权重矩阵为。

2 基于PCA-DELM 的入侵检测算法

2.1 PCA数据降维设计

主成分分析PCA（Principal Component Analysis）是统计学中的一种降维方法，它通过削减特征向量的数量降低矩阵维度。在神经网络中，可以采用PCA 减少输入数据样本的特征维度，从而降低神经网络模型计算量，提升模型计算速度 。假设给定原始数据集A={a11，a12，ai j，…，am n}，其中i代表样本数据，j表示对应样本的特征维度，m和n分别表示样本个数和特征数量，数据集矩阵可用式（12）表示。

PCA 采用线性变换将原始数据变量转变成非线性相关的数据变量。通过求出协方差矩阵的特征向量和特征值，保留累计贡献率超过85%的特征向量，用原始数据矩阵乘以特征向量矩阵得到一个新的特征矩阵，从而降低维度。式（13）定义了数据集中不同维度上的均值μ。

使用式（14）计算样本点在不同维度上的偏差。

数据集协方差矩阵H定义为。

对输入数据集协方差矩阵做奇异值分解（Singular Value Decomposition，SVD）可以得到一组特征值和特征向量(λ1，μ1)，(λ2，μ2)，…，(λn，μn)，它表示协方差矩阵H的n组特征值和特征向量，将原始数据映射到协方差矩阵中k个最大特征值所对应的特征向量张成的子空间中。式（16）给出了k的确定方法。

其中，β是子空间的特征值之和与原始空间的所有特征值之和的比值。选取最大的k个特征值后，可生成一个大小为m*k的矩阵B，按照式（17）将原始数据投影到k维子空间中。

式（12）—式（17）给出了去除不同特征间相关性的具体步骤。分别在两个数据集上调用上述方法实现降维。依据经验将β设置为0.85，并由式（16）在UNSW-NB15 数据集和CIDDS-001 数据集上分别保留前14、前6 个特征向量，这种方法在消除不同维度相关性的同时，还可减少模型在训练过程中的存储开销。

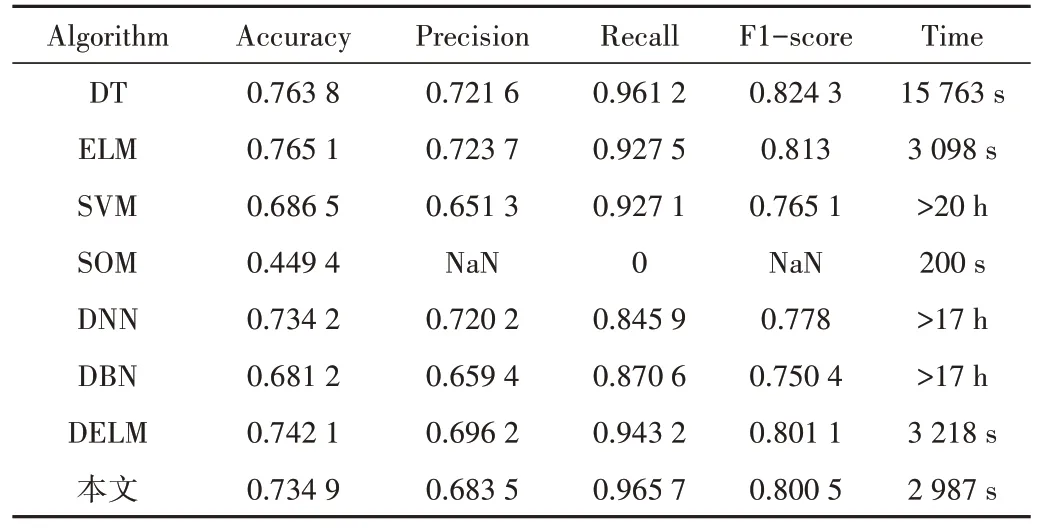
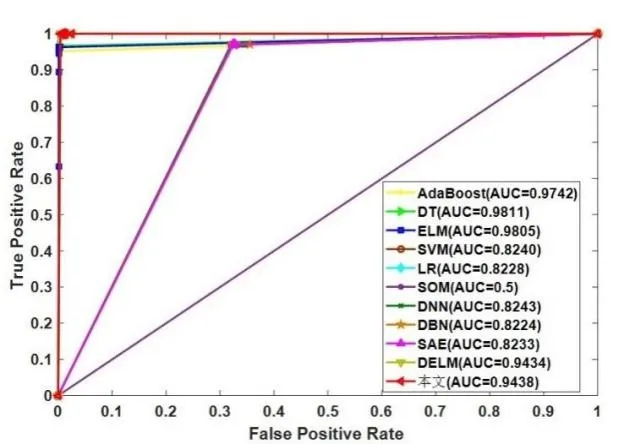
PCA 降维的时间复杂度为O(min(m3，k3))，m是样本数量，k为经PCA 降维后保留的子空间维数。显然，k

2.2 算法流程

本文提出的PCA-DELM 入侵检测算法需通过3 个阶段，检测前先对数据作预处理，然后用PCA 对数据集进行降维处理，最后通过具有深度学习能力的极限学习机（Deep Extreme Learning Machine，DELM）对数据进行监督分类，完成入侵检测过程。PCA-DELM 入侵检测流程包括以下步骤，流程如图3所示。

Fig.3 Flow of DELM intrusion detection图3 PCA-DELM 入侵检测流程

（1）数据预处理。标准化UNSW-NB15 和CIDDS-001数据集，对数据进行归一化处理后得到数值型数据，形成标准化数据集。

（2）定义DELM 神经网络模型参数。根据寻参实验结果可知，网络迭代100 次，隐含层共3 层，在7070-120 时，网络分类性能最佳。

（3）PCA 降维。对预处理后的高维数据集进行降维并得到低维表示的数据。

（4）数据分离。将降维后的数据按比例分为训练集、验证集、测试集。

（5）形成DELM 有监督分类模型，将训练集和验证集数据输入到DELM 分类模型中进行训练，调整模型。

（6）输出最优的DELM 分类模型。

（7）输入测试集数据并输出分类规范化结果。

3 实验设置与分析

本文共做了2 组实验。①在UNSW-NB15 数据集及CIDDS-001 数据集上进行二分类实验，在2 个数据集上验证PCA-DELM 入侵检测算法模型的分类检测性能；②在上述数据集上进行多分类实验，进一步验证该模型的网络分类性能及泛化能力，在实际包含不同攻击的复杂网络中对入侵行为的检测能力进行验证。

UNSW-NB15 数据集包含2×105条数据，共49 个特征。除正常数据外，还包含Fuzzers、Analysis、Backdoors、Dos、Exploits、Generic、Reconnaissance、Shellcode 及Worms 在内的9 种攻击。CIDDS-001 数据集包含6.8×105条数据，是来自于网络中的实时流量，包括在内部服务器（Web、文件、备份和邮件）和外部服务器（文件同步和Web 服务器）上捕获的实时流量，包括14个特征。

3.1 评价指标

为更好地评估本文模型及算法的有效性，在二分类实验中，将数据集中的攻击合并为Abnormal，记为2，正常数据Nornal 记为1。利用入侵检测准确率（Accuracy，Acc）、精确率（Precision，P）、真正率（True Postive Rate，TPR）、假正率（False Postive Rate，FPR）、F 值、召回率（Recall）等指标对二分类实验进行评价。具体计算方法参考文献［17］。

3.2 分类性能分析实验

实验环境为Windows10，64 位操作系统，处理器Intel（R）Core（TM）i5-6500CPU3.20GHz，安装内存（RAM）8.00GB，仿真环境是MatlabR2017b。在进行二分类和多分类实验前为验证PCA-DELM 的分类性能，与ELM、DELM方法在UCI 的Iris 和Wine 数据集上做了分类对比试验。本文提出的PCA-DELM 分类器在所测试的数据集上的分类精度不低于ELM 和DELM 分类器，在Iris 数据集上的分类准确率高达100%，在Wine 数据集上的分类准确率高达93%。

3.3 二分类实验

仿真实验中，使用UNSW-NB15 数据集和CIDDS-001数据集上进行入侵测试，将本文所提出的分类模型PCADELM 与ELM 分类模型、SOM 网络分类模型、深度神经网络分类模型（DNN、DBN）、经典机器学习分类器进行对比实验，通过各种评价指标对算法模型进行比较，验证算法模型的性能。将数据集分为训练集和测试集，进行入侵检测仿真实验，各算法在两个数据集上的二分类测试结果如表1、表2所示。

Table 1 UNSW-NB15 binary classification test results表1 UNSW-NB15二分类测试结果

Table 2 CIDDS-001 binary classification test results表2 CIDDS-001二分类测试结果

由二分类实验结果可知，在UNSW-NB15 和CIDDS-001 数据集上，PCA-DELM 入侵检测模型的测试准确率分别为73.49%、81.76%，在CIDDS-001 数据集上的准确率较高。PCA-DELM 方法在准确率方面十分稳定，波动较小，且处于较高的检测水平。

由表1 可知，在UNSW-NB15 数据集上，除SOM 方法外，其余算法检测准确率均达60%以上，由于该数据集较为分散，分类难度高，故准确率普遍偏低。其中，PCADELM 的准确率、精确率、召回率及F 值分别为73.49%、68.35%、96.57%、80.05%，与较为稳定的SVM 分类器相比分别高出4.84%、3.22%、3.86%、3.54%，在时间方面，PCADELM 用时要少19 h以上。

由表2 可知，DELM 方法的检测准确率最高，为99.25%，接近100%，比效果最差的SOM 高出81.01%，次优的分类模型为DBN，准确率为97.66%，在传统的机器学习分类器中，DT 表现最佳。PCA-DELM 的测试准确率在80%以上，且精确率、召回率为100%，时间为3 872 s，除去效果最差的SOM，时间在其余算法中最少。

综上，SVM 分类器的性能在不同的数据集上能够保持相同的范围，且维持较高的准确率。然而，PCA-DELM 分类模型的准确率与其他方法相比，在两个数据集上均较高且稳定，且高出0%～70.47%。当精确率和召回率发生冲突时，对模型性能的比较会困难得多，但F 值能够兼顾精确率和召回率，因此可看作是调和平均，以更好地对模型进行评价。实验结果表明，SVM 和DT 分类器表现较好，说明SVM 和DT 方法适合二分类问题，但深度神经网络总体性能明显优于经典机器学习算法，在二分类方面颇具优势。

3.4 多分类实验

本文使用的2 个数据集均为非平衡数据集，各攻击之间有所差异，故进行多分类实验，利用各种评价指标进一步分析各算法的入侵检测性能，验证比较算法模型可靠性。表3和表4为各算法模型多分类详细结果。

Table 3 UNSW-NB15 multi-classification test results（1）表3 UNSW-NB15多分类测试结果（1）

Table 4 UNSW-NB15 multi-classification test results（2）表4 UNSW-NB15多分类测试结果（2）

在UNSW-NB15 数据集上，包含正常数据和9 种攻击。对 于Normal，PCA-DELM 与DT 的AUC 值最高，分别为0.823 1、0.848 5，AUC 值最小的是SOM，为0.138 0。SOM、DELM、PCA-DELM 的真正率低于60%，其余算法高于64%，其中最高的是SVM 分类器，高达87.35%，但DT 和PCA-DELM 的假正率很低，分别为5.05%、12.98%。对于Fuzzers 攻击，SVM、DNN、SOM、DBN 的真正率为0%，除DNN 算法的假正率和AUC 值分别为0.5%、49.96%外，上述其余算法的假正率和AUC 值均为0%，ELM 的AUC 值最高，为79.43%。对于Analysis 攻击，除DT 算法的真正率为8.27%，其余算法的真正率均为0%，DT、ELM 的假正率分别为3.31%、0.64%，其余算法的假正率均为0%，各算法的AUC 值均在0.5 左右。对于Backdoors 攻击，DT、DELM、PCA-DELM 算法的真正率分别为24.87%、0.86%、1.21%，其余算法的真正率为0%，各算法的AUC 值均在0.5 左右。对于Dos 攻击，除ELM 算法的真正率最高为44.44%外，其余算法的真正率均低于22%，PCA-DELM 的效果最好，AUC 值最高，为0.783 2。对于Exploit 攻击，PCA-DELM 的真正率为78.1%，AUC 值为0.721 3，对于Generic 攻击，除SOM 算法外，其余算法的真正率均能达到95%以上，其中DBN 最高为96.95%，PCA-DELM 的真正率为96.43%，除SOM 算法外，其余算法模型表现较好，AUC 值均能达到0.8以上。对于Reconnaissance 攻击，所有算法模型的AUC 值均在0.5 以上，其中ELM 的真正率最高，为13.21%。对于Shellcode 攻 击，AdaBoost、DT 的真正率分别为7.14%、52.38%，假正率分别为0.2%、1.11%，其余算法的真正率和假正率均为0%，大部分算法的AUC 值为0.5，包括本文提出的PCA-DELM 模型。对于Worms 攻击，仅DT 的真正率为13.64%，其余算法均为0%，除DT 的AUC 值为0.567 7，其余算法的AUC 值为0.5。

在CIDDS-001 数据集上，对于Normal，PCA-DELM 的真正率高达95.99%，且AUC 值高达0.9649；对于Attackers，DELM 与AdaBoost 算法的AUC 值最高，分别为0.923 1、1，其余算法的AUC 值均在0.5 上下，所有算法的假正率趋近于0%或者为0%；对于Suspicious，除SOM 算法外，其余算法的真正率均达到85%以上，其中DNN 的真正率为100%，PCA-DELM 的真正率为97.31%，AUC 值为0.707 6，模型性能优于大部分其他算法模型；对于Unknown，PCADELM 的真正率仅31.55%，但其AUC 值为0.642 9，假正率低至2.98%，其余算法的AUC 值大部分集中在0.5 左右；对于Victim，DT、SOM 的真正率为100%，DELM 算法的真正率为99.45%，剩余算法的真正率为0%，DT、DELM 的AUC值分别为0.957 5、0.990 5，其余算法均低于0.6。图4 和图5 分别为两个数据集上的ROC 曲线，直观地说明了AUC 及真、假正率之间的联系。表5 为各算法在不同数据集上检测所花费的时间，显然，PCA-DELM 模型检测时间明显少于其他算法，更具实时性，在大数据时代下更具优势。

Table 5 Time execution evaluation indicators表5 时间执行评价指标

Fig.4 UNSW-NB15-Generic ROC curve图4 UNSW-NB15-Generic ROC 曲线

Fig.5 CIDDS-001-Suspicious ROC curve图5 CIDDS-001-Suspicious ROC 曲线

二分类实验及进一步的多分类实验结果表明，在准确性方面，PCA-DELM 模型性能明显优于经典神经网络和经典机器学习算法，在二分类和多类方面都有很大优势，在其他评价指标上也体现出较大优势。

4 结语

本文利用PCA 的降维能力，设计了一种基于主成分分析的强化深度极限学习机分类模型，并提出了PCA-DELM模型。一方面，使用PCA保证模型对数据的特征降维能力；另一方面，利用DELM 保证对数据快速分类的能力。实验结果表明：①PCA-DELM 入侵检测模型的数据分类性能稳定，不管是复杂高维数据，还是攻击类型多数据集，都能实现较优的入侵检测效果，且不敏感于特定数据集；②PCADELM 入侵检测模型成功解决了现有方法（数据挖掘、传统机器学习等方法）存在的准确率、精确率、召回率、真正率等指标偏低的问题；③在2 个网络入侵检测数据集上，PCADELM 入侵检测模型与现有方法相比，在各类评价指标上均具有明显优势。特别是在实时网络数据集CIDDS-001上仍能表现稳定。PCA-DELM 入侵检测模型为车联网、物联网等不同领域的安全问题方面提供全新、可行的解决方案及思路。本文采用的是有监督分类模型，因此对真实网络环境中未知攻击的检测还存在一定局限性。未来工作中，将考虑引入生成对抗网络（Generative Adversarial Networks，GAN）学习正常样本的检测入侵行为且不受限于特定样本的特性，以提升对未知攻击的检测率。