乡村振兴内部系统协同发展及动态演进研究——基于PVAR 模型与Kernel 密度估计方法

周文建，何翠香

(云南民族大学 经济学院,云南 昆明 650504)

改革开放以来，我国农村改革取得一系列重大成就，农业生产、农村面貌、农民生活发生了翻天覆地的变化。进入新时代后，以习近平同志为核心的党中央着眼党和国家事业发展全局、顺应亿万农民对美好生活的向往，提出实施乡村振兴战略。实施乡村振兴战略，是全面建设社会主义现代化国家的重大历史任务，是新时代“三农”工作的总抓手。习近平总书记高度重视乡村振兴战略，指出从世界百年未有之大变局看，稳住农业基本盘、守好“三农”基础是应变局、开新局的“压舱石”[1]，强调巩固拓展脱贫攻坚成果，全面推进乡村振兴，加快农业农村现代化，是需要全党、全国各族人民高度重视的一个关系大局的重大问题[2]，并多次针对乡村振兴的内涵、要求、目标、推进及问题作出具体的论述。乡村振兴有其丰富的内涵，纵向上包括脱贫攻坚阶段、巩固与拓展脱贫攻坚阶段、脱贫攻坚与乡村振兴有效衔接阶段和乡村振兴的进一步推进阶段，横向上则包含了“产业兴旺、生态宜居、乡风文明、治理有效、生活富裕”20 字总要求。

在此背景下，学术界对乡村振兴研究方兴未艾。通过对既往文献进行梳理，相关研究大致可分为两类：第一类为定性研究，主要集中在对乡村振兴理论逻辑梳理[3-6]、核心内涵[7-9]、战略实施途径[10-11]以及同脱贫攻坚相衔接[12-15]等方面。第二类为定量研究，关于此类研究又可以细分为两个方面，一是将乡村振兴同具体产业相结合，探究二者内在机制，进而丰富了乡村振兴战略意义。如何雷华等和张蕴萍等研究了数字经济对乡村振兴的作用机制并指出数字经济对乡村振兴具有赋能效果[16-17]。耿松涛等和申始占等从乡村旅游的视角论述了乡村旅游在助力乡村振兴的作用机制[18-19]。二是根据乡村振兴战略的总要求构建评价体系并对其进行研究，如张旺等测算了2010—2019 年我国乡村振兴水平后使用Dagum 基尼系数、Kernel 密度估计法对其深入探究，研究发现我国乡村振兴水平及各子系统的发展均在区域间存在一定差异[20]。芦风英等则使用 Dagum 基尼系数解析了中国乡村振兴发展的区域差异大小及来源[21]。其结果同张旺等研究结论一致。徐雪等则从乡村振兴水平及各子系统水平的区域差异及演进趋势做了细致研究，研究发现乡村振兴水平存在差异源于区域间差异，而各子系统的区域差异均呈缩小趋势，子系统间的差异也主要来源于区域间差距[22]。另有学者通过人地关系地域系统理论和人地系统科学考察了中国县域乡村振兴水平的空间格局，进而提出了新时代乡村振兴的关键问题及其路径对策[23]。张琦等则在《国家乡村振兴战略规划（2018—2022 年）》已有评价指标体系基础上，对现有乡村振兴评价体系进行了优化[24]。除上述外，学界还从新型城镇化建设角度进行了深入的探讨[25-26]。

现有研究均对乡村振兴战略进行了有益探索。综观现有文献，发现对乡村振兴自身的理论逻辑梳理、核心内涵、战略实施途径以及同脱贫攻坚相衔接等方面的研究居多，关于乡村振兴的评价体系及测度的学术成果亦不少，重点关注在乡村振兴总体评价指标和区域差异方面，鲜有研究乡村振兴系统内部子系统的协同发展与动态演进，且所使用数据主要为省级层面数据。乡村振兴作为一个系统，其每一次发展将“牵一发而动全身”。鉴于此，本文选择2000—2022 年全国各地级市数据，采用熵值法对数据进行指数测算，构建PVAR 模型并结合Kernel 密度估计分析我国乡村振兴及其内部子系统的协同发展和动态演进规律，依托数据的细化以及样本量充足，以期更深入细致地掌握我国乡村振兴水平及其子系统发展水平的变化趋势及差异性，进而提出更加准确的决策支持。

一、研究设计与数据说明

（一）模型构建

Douglas Holtz-Eakin 等人在研究美国两个男性样本中工资和工作时间之间的动态关系时，首次对面板数据中向量自回归系数的估计和检验，并将工具变量应用于准差分方程中进行回归估计[27]，后续由Love 等与Yujun L 等对其进行不断研究拓展[28-29]，由此面板向量自回归（PVAR）模型开始在学界被广泛应用。而PVAR 模型的优点得益于继承和发展了VAR 模型的优势，即在PVAR模型中不需要事先明确变量之间的因果关系，而是通过将所有变量视为内生变量，并分析每个变量及其滞后变量对模型中其他变量的影响关系。同时，PVAR 模型能够有效识别面板数据中个体间的相关性和异质性，因此能够更加准确地捕捉数据间的动态关系[30]。鉴于此，本文选取PVAR模型研究乡村振兴子系统间动态影响关系。构建的PAVR 模型如下所示：

式（1）中，Yit为乡村振兴子系统1×5 阶列向量。包括产业兴旺水平（Thr_i）、生态宜居水平（Eco_l）、乡风文明水平（Civ_v）、治理有效（Eff_g）和生活富裕水平（Pro_l）。下标i为全国各地级市；t为2000—2022 年。j为滞后阶数，Yi,t-j为滞后j阶的变量，Aj为滞后j阶的系数矩阵，βi个体固定效应，γi为时间固定效应，εit为随机扰动项。

（二）变量选取

习近平总书记在党的十九大报告中首次提出了乡村振兴战略，将产业兴旺、生态宜居、乡风文明、治理有效、生活富裕作为乡村振兴战略总要求[31]。学术界对此展开了深入研究；李志龙从乡村振兴战略的总要求出发将乡村振兴划分为上述总要求对应的五个子系统[32]；张挺等则根据既往研究结论及国家政府文件通过德尔菲法以专家打分的方式筛选出评价指标[33]；而张旺等则使用了熵值法对遴选出的评价指标进行测算[34]。基于此，本文借鉴相关学术研究成果及国家政府文件，遴选出16 个维度30 个具体指标来构建的乡村振兴各子系统评价体系，为避免各指标权重主观赋权和数据冗余等问题，采用熵值法对乡村振兴各子系统评价指标进行赋权。详见表1。

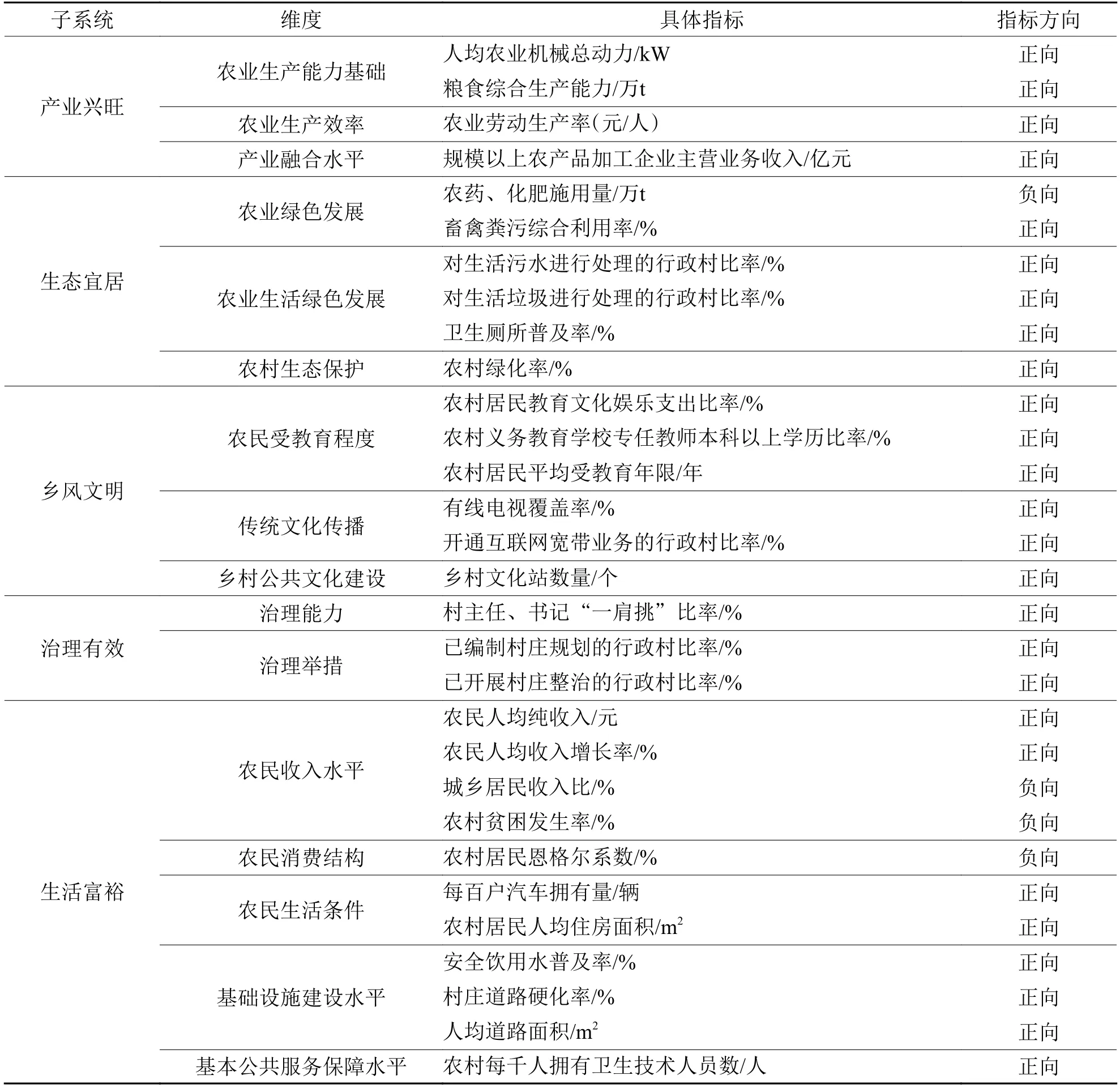
表1 乡村振兴各子系统评价体系

（三）数据来源与描述性统计

鉴于数据的有效性及可获得性，本文主要数据来源为《中国城市年鉴》《中国统计年鉴》《中国农村统计年鉴》《中国人口和就业统计年鉴》《中国第三产业统计年鉴》《中国农村统计年鉴》《中国教育统计年鉴》以及各省市统计年鉴、统计公告，个别缺失数据采用线性差值法补全。将数据梳理、整理后得到2000—2022 年全国各地级市数据（不含港澳台地区）①由于我国香港、澳门特别行政区及台湾地区数据存在明显缺失，本文研究仅选取了部分省市。，凭借此数据对我国乡村振兴内部子系统的影响关系进行系统探究。为避免异方差及序列相关对模型带来的影响，对所有数据进行上下1%的winsorize 处理。表2 为我国乡村振兴子系统各个变量的描述性统计特征，Thr_i为产业兴旺水平，Pro_l为生活富裕，Eco_l为生态宜居，Civ_v为乡风文明，Eff_g为治理有效。

表2 乡村振兴子系统各个变量的描述性统计结果

二、实证研究

（一）平稳性检验与模型最佳滞后期选择

在对模型进行回归估计前，需对模型中所有变量做单位根检验，避免后续模型回归可能产生的伪回归等问题。参照刘志华等人的做法[35]，对模型中所有变量进行单位根检验，检验结果由表3 所示。模型中所有变量均为一阶单整，故可建立面板向量自回归（PVAR）模型进行后续实证研究。

表3 面板数据单位根检验

借鉴连玉君等人的研究方法[36]，使用PVAR2 Stata 程序包，通过AIC、BIC 以及HQIC 信息准则确定PVAR 模型的最优滞后阶数，由表4 结果可知，滞后2 期为模型最优滞后期，因此可建立PVAR（2）模型。

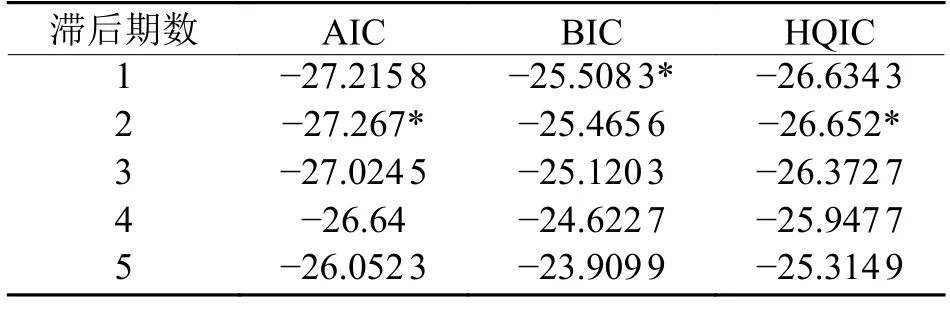
表4 最优滞后期数

（二）PVAR 模型分析

1.PVAR 模型的GMM 估计与稳健性检验

为确保滞后各变量与被解释变量之间正交且与误差项不相关，在选取最优滞后阶数后对模型进行“Helmert procedure”变换。进而利用GMM对模型进行参数估计。表5 为各变量GMM 估计的详细结果。

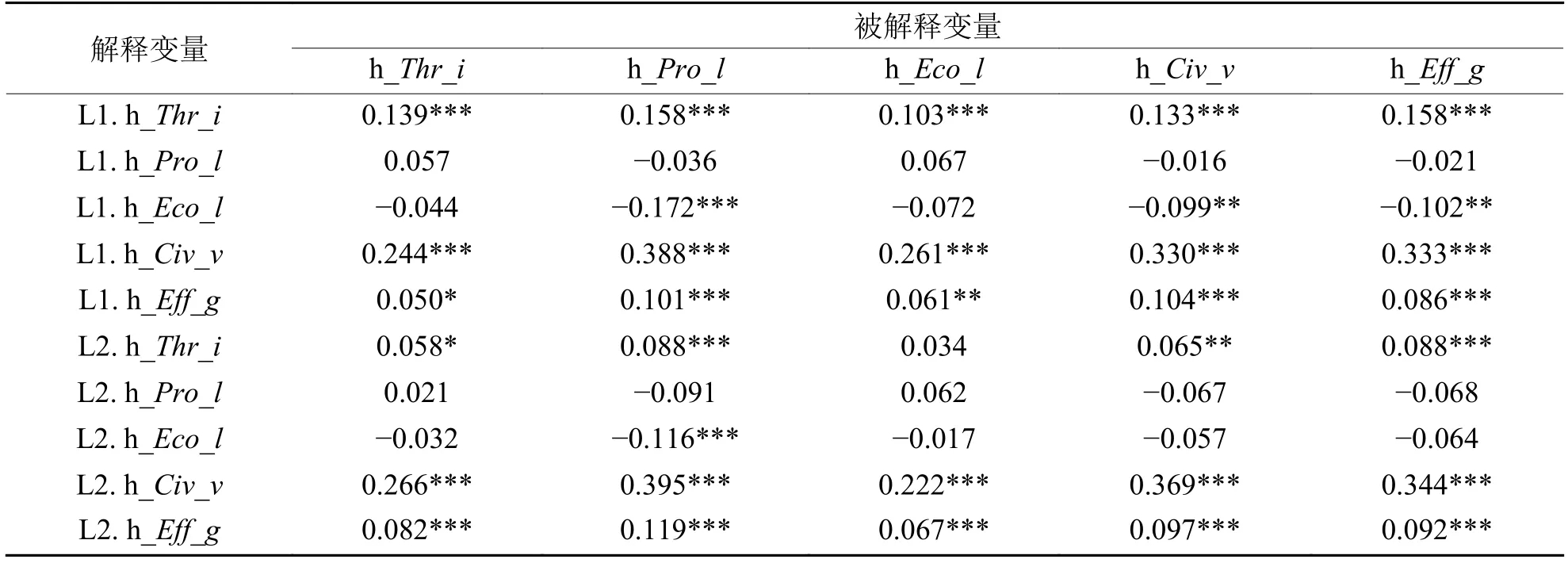
表5 PVAR 模型的GMM 估计结果

第一，从各变量对自身的影响程度看，产业兴旺水平其滞后一阶、二阶回归系数均显著为正，表明产业兴旺作为乡村振兴的重点，其对乡村振兴的影响是持续的，并且在未来一段时间内对其仍具正向影响。而生活富裕水平、生态宜居水平其滞后一阶、二阶回归系数均不显著；乡风文明水平及治理有效水平各滞后一阶、二阶回归系数均显著为正，以上实证结果表明乡村振兴子系统中产业兴旺、乡风文明以及治理有效对乡村振兴的发展都具有持续性的正向作用；对此，应当继续加强对各个子系统间的协同性，切实提高农村居民生活富裕水平，进而完善人居环境水平，使各个子系统能够长期为乡村振兴的发展提供强有力的动力，有效巩固脱贫攻坚成果。

第二，从各子系统的相互影响关系看，当产业兴旺水平作为被解释变量时，乡风文明、治理有效的滞后期均能促进产业兴旺水平发展。而生活富裕与生态宜居的滞后期对于产业兴旺的发展影响却不显著。当生活富裕水平作为被解释变量时，产业兴旺水平、乡风文明水平以及治理有效水平的滞后均对其产生了显著的正向影响，生态宜居水平则负向显著。当生态宜居水平作为被解释变量时，乡风文明、治理有效的滞后期均正向显著，而产业兴旺则滞后一期显著，滞后二期不显著。当乡风文明水平作为被解释变量时，产业兴旺、治理有效的滞后期均正向显著，而生态宜居滞后一期则负向显著，滞后第二期则不显著，同时生活富裕的滞后期则均不显著。当治理有效水平作为被解释变量时，产业兴旺、乡风文明的滞后期均正向显著，生态宜居则滞后一期负向显著，滞后二期不显著，生活富裕则不显著。

为了检验模型的稳定性，通过比较模型的特征根是否都落入单位圆进而来说明模型是否具有较强的稳定性（图1），伴随矩阵的特征根均落入单位圆内（最外围特征根的模为0.991），则证明PVAR 模型是稳定的。

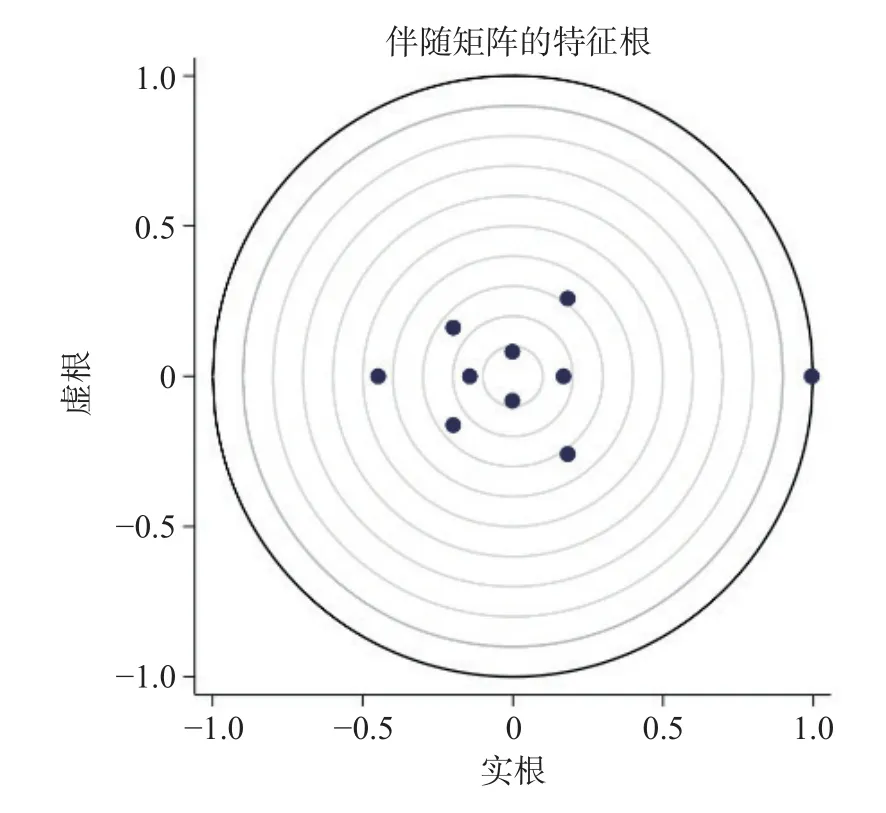
图1 PVAR 模型稳健性检验

2.脉冲响应函数分析

通过上述GMM 估计结果对乡村振兴各子系统之间的静态比较分析，初步探究了乡村振兴子系统间的相互影响关系，为进一步探究乡村振兴各子系统间的相互影响关系，通过Monte-Carlo 法迭代200 次后得到了全国乡村振兴各子系统间的脉冲响应图（图2），横坐标S 表示滞后期数（0～10 期），图中上下两条实线表示95%的置信区间，中间实线则表示了各变量受到1 个标准差的冲击时的响应效果。

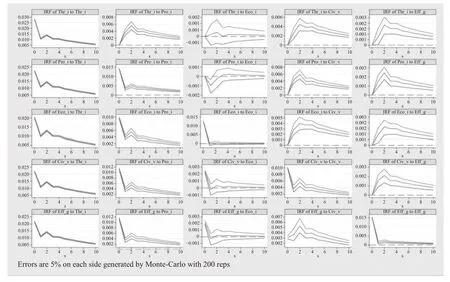
图2 脉冲响应函数图

首先，当产业兴旺水平、生活富裕水平以及乡风文明水平在受到自身1 个标准差冲击时，均在当期达到最大值，滞后1 期时有所下降，滞后2 期时重新达到峰值，随后逐渐回归到0 值附近。表明产业兴旺水平、生活富裕水平以及乡风文明水平均有相应的正反馈调节机制，使其在一段时间内保持一定的偏离状态。当生态宜居水平和治理有效水平在受到自身1 个标准差冲击时，同样也在当期达到最大值，但随后滞后期均回归到0 值附近，表明生态宜居水平和治理有效水平对于自身的发展亦具有较强的持续性作用，并且具有一定的韧性和稳定性。

其次，当产业兴旺水平分别受到各个子系统的1 个标准差冲击时，均在当期达到最大值。随后滞后一期有所回落，滞后两期时重新达到峰值，随后逐渐回归到0 值附近，由此表明产业兴旺水平具有相对稳定的发展态势，能够与各个子系统协调发展并逐步提升乡村产业的竞争力和发展潜力。

当生活富裕水平受到产业兴旺水平的1 个标准差的冲击时，当期并没有反应，滞后一期时开始正向响应，滞后第二期达到峰值，随后逐渐回归到0 值附近，则表明产业兴旺水平对生活富裕的影响有一定的滞后期，但后续发展能够稳定促进生活富裕水平的发展。而当生活富裕水平受到其他3 个子系统的1 个标准差冲击时，同样在当期达到最大值，滞后1 期时有所下降，滞后2 期时重新达到峰值，随后逐渐回归至0 值附近。表明各子系统对促进生活富裕水平的发展能够提供持续的推力。

当生态宜居水平受到各子系统的1 个标准差的冲击时，冲击反应均迅速，但存在略微差异，即当受到产业兴旺水平冲击时，在滞后两期时达到峰值且为正向影响，随后逐渐回归于0 值附近；而当受到生活富裕水平冲击时，在滞后一期达到峰值且为负向冲击，后随滞后期逐渐回归于0 值附近；当受到乡风文明水平和治理有效水平冲击时，均在当前达到最大值，后续回归于0 值附近。表明生态宜居水平与其他四个子系统间存在较强的协调能力，并能持续促进生态宜居水平的发展。

当生态宜居水平在受到各个子系统的1 个标准差的冲击时，均在滞后两期时达到峰值，后随滞后期逐渐回归至0 值附近；治理有效水平受到各子系统的1 个标准差的冲击时亦是如此，表明乡风文明水平与治理有效水平与其他3 个子系统间均能够协调发展。

基于以上分析，乡村振兴各子系统间均趋于协调发展水平，并能共同促进乡村振兴水平的发展。这一结论与徐雪等人的[22]研究结论一致。

3.方差分解结果

为更进一步考察乡村振兴各子系统间的贡献力度，对PVAR 模型进行方差分解（表6），为便于比较，选取滞后10 期、20 期以及30 期来考察乡村振兴各子系统的相互贡献率。

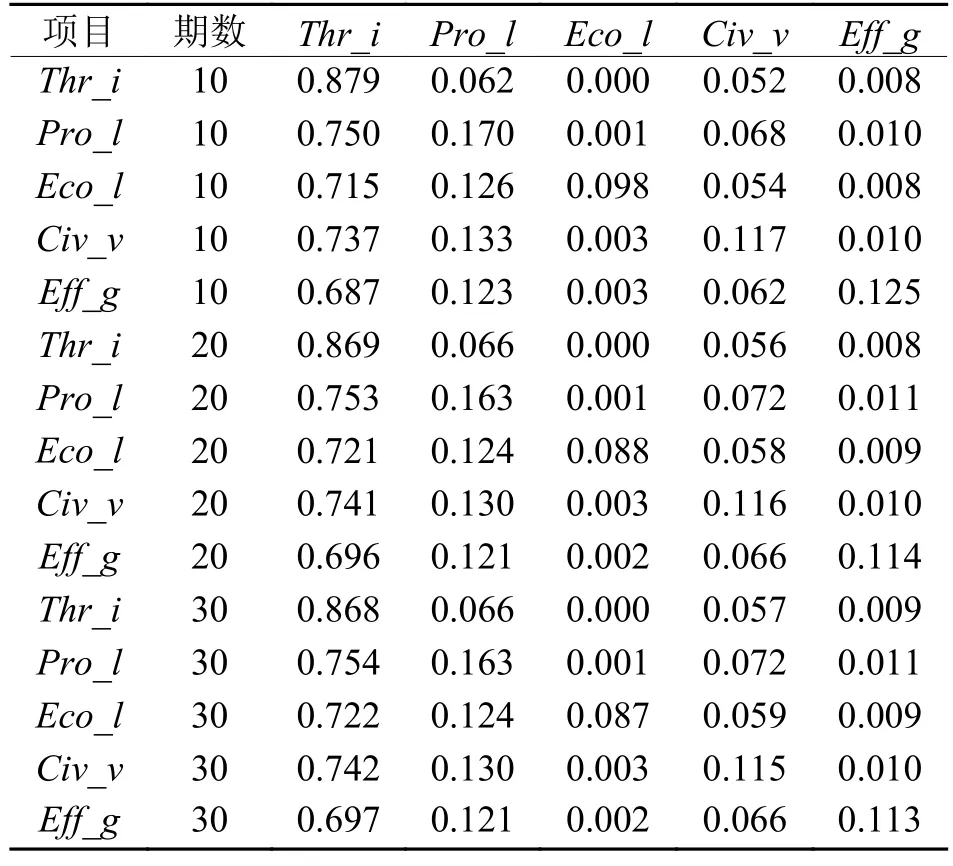
表6 方差分解结果

就各子系统自身而言，其方差贡献率主要均来源于自身，产业兴旺水平在第30 期时受到自身的方差贡献率高达86.8%，而其他4 个子系统在第30 期受到自身的方差贡献率分别为16.3%、8.7%、11.5%、11.3%；

从各子系统间的相互贡献程度看，产业兴旺水平受到其他子系统的方差贡献率比率均较高，且在第20 期后基本稳定。生活富裕水平对于自身的方差贡献率则在第20 期后一致保持稳定于16.3%。生态宜居水平受到其他子系统的方差贡献率则不足1%。乡风文明水平受到各个子系统的方差贡献率在第20 期后基本一致，分别为5.7%、7.2%、5.8%、6.6%。而生活富裕水平受到各个子系统方差贡献率第10～30 期均在1%左右。

三、发展态势、极化现象及延展性分析

为进一步考察乡村振兴各子系统间的绝对差异特征，本文利用MATLAB R2023a 进行Kernel 密度估计并绘制出三维核密度估计图，进而对乡村振兴各子系统在各时点发展态势、极化现象以及延展性做进一步分析。

（一）Kernel 密度估计

借鉴沈丽等的研究方法[37]，首先构建乡村振兴水平函数f（g）如下：

式（2）中，n为模型中所有观测个体数，Gi为独立同分布的观测值，φ为带宽，为均值。K(·)为核函数，核函数表达式如式（3）所示。本文选用高斯核密度函数对乡村振兴子系统进行估计，并令 φ=0.05，绘制出全国乡村振兴发展水平（图3）以及各子系统发展水平（图4）。

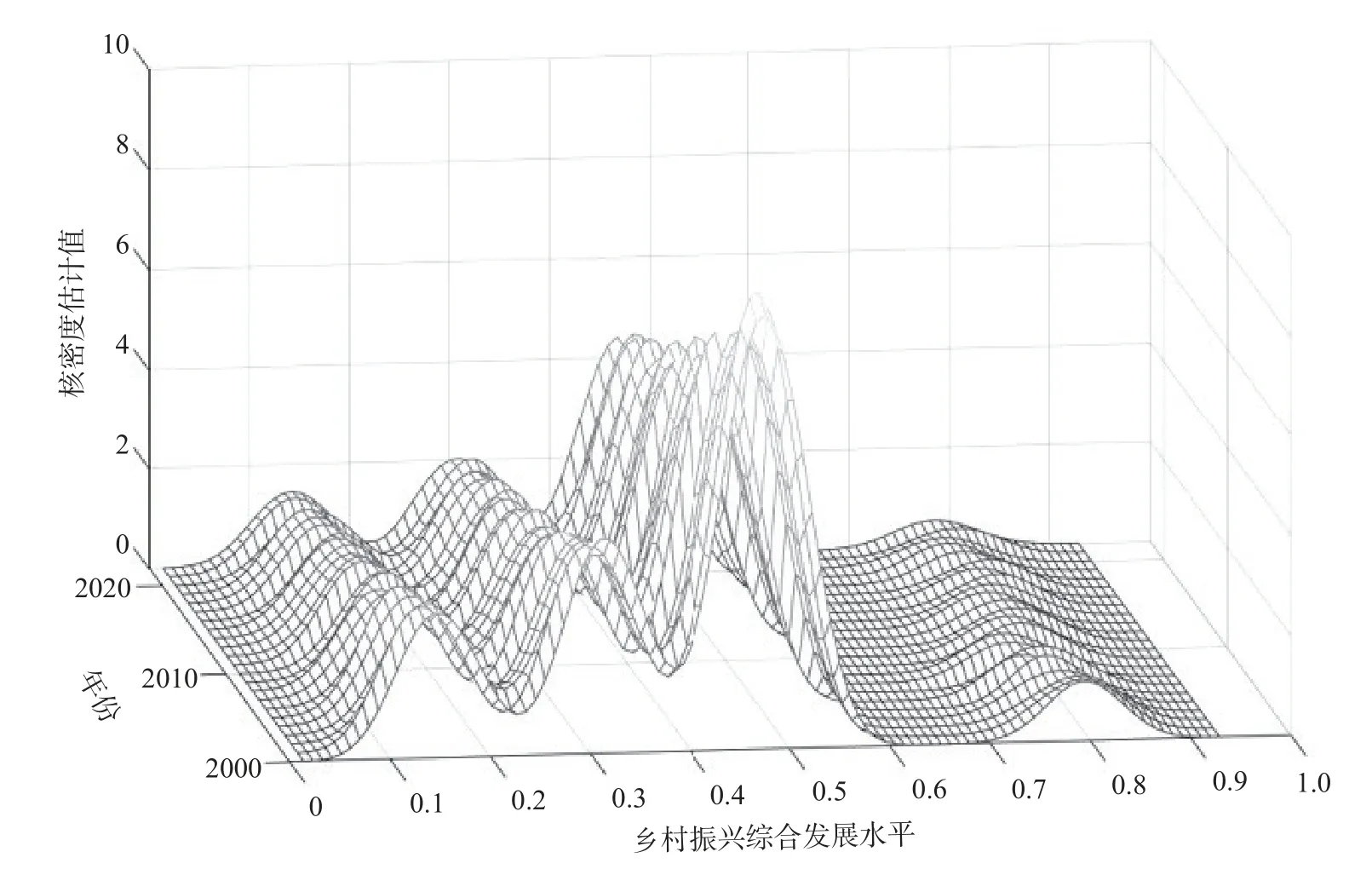
图3 乡村振兴综合发展水平

（二）分布动态演进分析

图3 为我国2000—2022 年全国各地级市乡村振兴综合发展水平的动态演变过程，通过对其分布态势、分布延展性以及极化现象进行分析，可以得到以下结论：首先，从分布态势看，乡村振兴综合发展水平的峰值呈“增大—增大—减小”，主峰宽度则呈“缩小—扩大”；表明我国乡村振兴综合发展水平在2000—2022 年间发展迅速，但随后发展速度有所下降，同时主峰宽度的变化也表明我国乡村振兴综合水平存在区域差异，这一结果也与张旺等研究结论一致[20]。其次，从乡村振兴的分布延展性看，2000—2022 年我国乡村振兴综合发展水平均右拖尾，且在拖尾处还存在较小峰值，表明由于政策时滞或资源禀赋等因素的影响，使得乡村振兴水平在部分地区发展水平更高，最后从极化现象看，乡村振兴水平则呈多峰态，其主要原因可能是我国农村地区分布较为分散，同时由于经济发展水平、资源禀赋等众多影响因素的制约，造成了区域间乡村振兴水平发展的极化现象，这一结果也与徐雪等研究结论一致[22]。

图4 为2000—2022 年我国乡村振兴各子系统的动态演变过程，图4（a）产业兴旺水平以及图4（e）治理有效水平，在其右拖尾处峰值分布差异较为明显，可能的解释为产业兴旺水平大多依托于地方资源或原有产业的发展，同时由于地域、政策时滞等因素也造成了治理有效水平的动态差异。而图4（b）（c）（d）分别为生活富裕水平、生态宜居水平以及乡风文明水平，总体发展态势与乡村振兴综合发展水平一致。因此从以上对乡村振兴综合发展水平及其子系统发展水平的动态分布情况看，我国乡村振兴子系统对整体乡村振兴水平的贡献相对均衡，政策和措施在不同地域、领域的实施相对成功，在我国农村地区的发展和治理取得了较好的效果。

四、结论与政策建议

综上，基于乡村振兴战略的深刻内涵构建了PVAR 模型，并使用2000—2022 年我国各地级市数据从静态和动态两个维度探究了乡村振兴各子系统间的影响关系；为进一步研究乡村振兴各个子系统的发展趋势，又利用Kernel 密度估计法对乡村振兴综合发展水平及其各子系统的动态演进过程进行了比较研究。

（一）结论

第一，从静态、动态两个维度看产业兴旺水平作为乡村振兴的重点，有效促进了各子系统的发展且持续性较强；生活富裕水平作为农村居民生活水平的具体表现，生态宜居水平则对其发展有所制约，但各子系统均能够对其发展提供持续推力；而生态宜居水平对生活富裕水平影响并不显著，但其能有效促进各子系统发展且持续性亦较强；乡风文明水平及治理有效水平则能长期促进各子系统发展。第二，Kernel 密度估计对乡村振兴综合发展水平及其各子系统的动态演进过程所做的比较分析表明，我国乡村振兴综合发展水平总体呈多极化、多峰状且存在右拖尾，各子系统动态演进过程均与乡村振兴综合发展水平动态演进过程基本保持一致，表明各子系统间发展虽存在一定差异，但能够协调发展，共同促进乡村振兴战略进一步发展。

（二）政策建议

（1）产业兴旺作为乡村振兴的重点，应持续发挥其乡村振兴战略“带头”作用，结合当地地域特点、资源、人文等多种因素，因地制宜，因材施教，鼓励农村特色产业建设，并定期给予技术、资金及人才支持，通过产业“带动”效应，提升农村生活水平、居住环境水平，使其能够最大化助推各子系统间的协调发展，进而削弱由地域、资源以及政策时滞所造成的产业极化现象。

（2）鉴于我国脱贫攻坚刚刚完成，农村地区基础建设薄弱，对此应鼓励农村居民就地就业，如积极参加农村特色产业的建设及村庄治理等工作，进而有效完善生态宜居及乡风文明水平，同时应加强农民职业技术培训教育，增加农民就业竞争力，切实促进农民增收，提高农村居民生活富裕水平。

（3）生态宜居与乡风文明相辅相成。在注重农村产业建设及生活富裕水平提高的同时，应当协调好生态环境的治理工作以及加强农村地区的思想文化教育、社会风尚等工作，巩固好、稳定好生活富裕水平的发展，进而完善农村产业建设，有效促进农民增收，最终确保乡村振兴战略的长期可持续性。

（4）当地政府、村委会应强化其职能，引导和监督好乡村振兴战略的有效实施，同时，由地域特征、地区资源等因素造成的政策时滞，则应给予相应的补贴或帮扶政策。进而协调好乡村振兴各个子系统间的相互影响关系，共同助力乡村振兴战略在我国农村地区的有效实施。