基于Sobol法的阮桥闸安全影响因素敏感性分析
刘德高,刘向宇,胡林生,王亚妮
(1.水发规划设计有限公司,济南 250014;2.淮安市水利勘测设计研究院有限公司,江苏 淮安 223005)
0 引言
水闸是建在河流或渠道上的低水头水工建筑物,通过水闸控制流量和调节水位。水闸在抵御上游洪水、保障下游生产生活用水安全等方面均扮演着极其重要的角色。然而,由于存在防洪标准低、水闸混凝土结构老化或严重损坏等问题,会对水闸的安全运行和效益发挥造成严重影响,水闸一旦失事将会严重影响当地社会经济的发展与稳定。因此,对水闸结构安全性进行研究显得十分必要。
对水闸结构安全性的研究分为确定性分析与不确定分析。在对水闸结构的确定性分析中,马飞等[1]对水闸安全性分析时,考虑了水闸自重、水压力、扬压力、浪压力和风荷载;曹邱林等[2]通过有限元软件对闸室结构的应力应变情况进行了研究,考虑结构自重、回填土荷载和水荷载。考虑水闸结构的不确定性,许萍等[3]考虑钢筋混凝土容重、上下游水位、底板与地基之间的摩擦系数对水闸结构安全的影响;张俊芝等[4]将水闸底板与地基土间的摩擦系数、钢筋混凝土的容重、上下游水深作为影响因素,分析了影响因素不同概率分布形式下的闸室稳定可靠度。
在对水闸安全分析时,考虑影响因素的不确定性十分有必要。水闸在其运行过程中,水位等外部因素受降雨、蒸发、温度等影响,水位变化呈现出一定的规律性变化。钢筋混凝土的变形模量等内部因素也并非始终保持不变,而是会随着材料的老化而逐渐降低,甚至可能因材料的屈服而发生突变。因此,无论是外部环境还是内部材料都会因其自身的不确定性而影响水闸的运行状态。
1 水闸安全评价指标及其计算方法
《水闸设计规范》(SL 265-2016)规定,水闸安全应满足以下要求[5]:①水闸沿基底的抗滑稳定安全系数应大于规范规定值;②最大基底应力应小于地基允许承载力的1.2倍;③最小基底应力应小于地基允许承载力。 因此,根据以上规范对水闸安全的要求,选定抗滑稳定安全系数、最大基底应力以及最小基底应力作为水闸安全评价指标。根据《水闸设计规范》(SL 265-2016),各个安全评价指标计算公式如下:
(1)水闸抗滑稳定安全系数计算:
(1)
式中,Kc为抗滑稳定安全系数;∑G为竖向荷载;φ为基底与地基间的摩擦角;C0为基底与地基间的粘聚力;A为基底面的面积;∑H为水平荷载。
(2)水闸最大基底应力与最小基底应力计算:
(2)
(3)
式中,Pmax与Pmin分别为最大基底应力和最小基底应力;∑M为所有荷载对于基底面垂直水流方向的形心轴的力矩;W为基底面对于垂直水流方向的形心轴的截面矩。
2 水闸安全影响因素选取
依据《水闸设计规范》(SL 265-2016),水闸安全计算工况及其对应的荷载组合见表1。
如今,广州“好教育”这颗星在持续发光、发亮,基础教育、高等教育、职业教育、民办教育及特殊教育全面布局,并且都得到了长足发展;一大批义务教育特色学校走上前台;师资流动更加科学,教育均衡成果显著,择校热大幅度降温……与此同时,5年来,好教育的推进使得一大批家门口的好学校脱颖而出,还培养了578名“卓越校长”,出现了一个个杰出校长群落,涌现出了一大批优秀教师典型代表,也出现了一大批全面发展、特长突出的好学生。

表1 水闸安全计算工况及对应的荷载组合
根据水闸安全评价各指标计算公式和所考虑的荷载,总结归纳出以下10个影响因素:钢筋混凝土容重x1、上游水深x2、下游水深x3、淤沙浮容重x4、上游泥沙淤积厚度x5、淤沙内摩擦角x6、风速x7、风区长度x8、地基土摩擦角x9和粘聚力x10。水闸安全评价各指标所涉及的影响因素见表2。
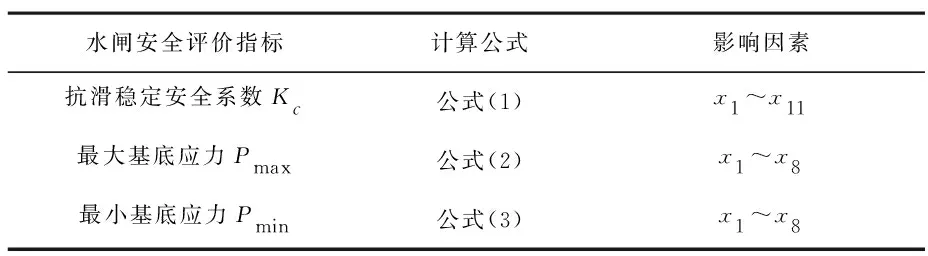
表2 水闸安全评价指标及其影响因素
3 Sobol法原理
Sobol法是由俄罗斯学者于1993年首次提出的一种全局敏感性分析方法[6]。Sobol法的核心思想是通过将模型进行分解,形成单个参数及参数之间组合的函数形式,并分别计算单个输入参数或参数集对输出方差的贡献,从而确定参数的重要性和交互作用。Sobol法通常适用于非线性、非单调函数模型,能够快速地计算出各个输入参数对响应值的一阶、高阶以及总阶系数,目前在水利、环境领域得到广泛应用[7-8]。
Sobol法假设模型结构表示为函数u=f(x),其中模型参数x=x1,x2…xn,可视为n维离散点,u为标量输出。假设函数f(x)可积,xi在[0,1]上服从均匀分布,且f(x)满足:
(4)
式中,k=i1…is。
则函数f(x)的方差分解表达式可以表示为:
(5)
式中,1≤i1 类似地,模型的总方差也可以分解为单个参数和多个参数相互作用的组合: (6) 将上式归一化即可得到各参数之间相互作用的敏感性: (7) (8) (9) 式中,Si表示参数xi单独作用时是敏感度;Sij表示参数xi与xj相互作用的敏感度;STi为参数xi和其他参数共同作用的敏感度;D~i表示除参数xi外其他参数共同作用产生的方差;其余变量含义同前所述。 拉丁超立方抽样[9]是一种高效的随机抽样方法,用于在多维空间中均匀抽取一组样本点。拉丁超立方抽样通过将每个维度分成若干等分,然后在每个等分内随机抽取一个样本点,保证了每个维度上的样本点分布均匀且互不重复。同时,拉丁超立方抽样还通过对不同维度的样本点进行组合,产生多个不同的样本组合,从而提高了采样的效率和可靠性。拉丁超立方抽样常用于模拟实验、优化问题、参数估计等领域,是一种非常有用的随机采样方法[10-11]。拉丁超立方抽样的步骤如下: (1)确定样本点数量和样本维度:确定需要抽取的样本点数量和样本维度。 (2)分割样本空间:将每个维度分割成相等的区间,得到一个二维的格点矩阵。 (3)随机抽取样本点:在每个维度的每个区间内随机抽取一个样本点,保证每个维度上的样本点分布均匀且互不重复。 (4)组合样本点:将每个维度上的样本点随机组合,得到多个不同的样本组合,从而提高了采样的效率和可靠性。 (5)应用样本点:将得到的样本点投入使用。 阮桥闸地处江苏省金湖县前锋镇,上游白马湖,下游宝应湖,设计流量69.3 m3/s。阮桥闸主要承担防止白马湖地区发生内涝和通航等功能。水闸为钢筋混凝土结构,本工程等别为Ⅲ等,永久性主要建筑物级别为3级,次要建筑物级别为4级,临时建筑物级别为5级,水闸地基土质主要为堤身填土。水闸底板顺水流向长为11 m,垂直水流向宽15.2 m,厚度为1 m,水闸底部高程为3 m,顶部高程为12 m。该水闸顺水流方向剖视图如图1所示。上游设计水位为6.50 m,下游设计水位为5.70 m。 图1 阮桥闸结构顺水流方向剖视 根据阮桥闸的相关工程资料,10个水闸安全评价指标影响因素概率分布的统计特征参数如表3所示,假定各个影响因素均服从正态分布且相互独立。 表3 影响因素的统计特征参数 首先,依据表3中各个影响因素概率分布的统计特征参数信息,采用拉丁超立方抽样方法对其抽取6000组样本;然后,利用水闸安全评价指标计算公式分别计算出每一组样本对应的安全评价指标值;最后,利用Sobol法对阮桥闸各项安全评价指标影响因素的敏感性大小进行定量评估,影响因素对安全评价指标的影响程度大小一般由总敏感性系数来衡量。阮桥闸安全评价指标影响因素的敏感性大小分析结果如表4所示。 由表4可知:对于抗滑稳定安全系数,上游水深的总阶敏感性系数为0.936,在所有影响因素中最大,表明上游水深对抗滑稳定安全系数影响程度最大,下游水深次之;对于最大基底应力,上游水深的总阶敏感性系数为0.874,在所有影响因素中最大,表明上游水深对最大基底应力的影响程度最大,下游水深次之;对于最小基底应力,下游水深的总阶敏感性系数为0.484,在所有影响因素中最大,表明下游水深对最小基底应力的影响程度最大,上游水位次之,总阶敏感性系数为0.407。 本文选取水闸抗滑稳定安全系数、最大基底应力与最小基底应力作为水闸安全评价指标,根据安全评价指标计算公式与所考虑的荷载总结出10个影响水闸结构安全的因素,采用Sobol法对阮桥闸的安全性影响因素进行敏感性分析。分析结果表明:对于抗滑稳定安全系数,上游水深对其影响最为明显,其余因素对其影响均不明显;对于最大基底应力而言,上游水深对其影响最为明显,其余因素对其影响均不明显;对于最小基底应力而言,下游水深与上游水深对其影响较为明显,其余因素对其影响均不明显。本文分析成果可为水闸安全运行提供有价值的参考。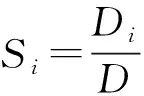
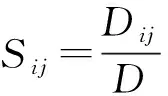

4 拉丁超立方抽样原理
5 工程实例
5.1 工程概况


5.2 敏感性分析结果
6 结论

