消费资本资产定价模型与“股票溢酬之谜”——基于我国资本市场的实证分析

储成兵

(安徽财经大学 会计学院,安徽 蚌埠 233030)

一、引言

自20世纪30年代以来,消费行为始终是经济学研究的焦点。凯恩斯[1](P79)于1936年开创性地提出了绝对收入理论,认为消费是由当期的可支配收入决定的,即随着即期收入的增加,人们往往会提高消费,但由于边际消费倾向递减规律,通常会导致更高比例的收入被储蓄而不是被消费。Modigliani[2](P146)基于生命周期假说,认为理性的消费者为了实现其一生效用最大化,在其拥有的总收入约束下追求消费的平稳。Friedman[3](P92)认为消费者的消费取决于其所预期获得的永久性收入,暂时性收入对其消费的影响不大。20世纪70年代后期,学者们将消费选择的研究从确定性状态拓展到不确定性状态,有关消费理论的研究更接近于实际情况,如,随机游走假说、流动性约束假说等等。其中一个重要的研究方向是Breeden提出的基于消费的资本资产定价模型(CCAPM)。CCAPM的核心思想是:风险资产所提供的超额收益率与其消费贝塔成正比。在CCAPM模型中,由于消费者的选择对象除了消费、无风险储蓄,还包括具有不确定性收益的风险资产,因此消费者跨期最优化选择是在一个不确定性的条件下作出的,理性消费者在其预算约束条件下在消费和投资之间作出选择,这样最优解既包括消费者均衡时的边际替代率,也包括资产的均衡价格,从而投资者通过考虑风险和收益的关系来确定资产定价。但CCAPM同时也带来了“股票溢酬之谜”,Mehra等[4](P145-161)利用1890—1979年美国的数据进行实证研究发现:美国股票市场平均年化收益率比同期无风险收益率高约6%,在同一时期,消费增长的标准差为0.036,股票市场超额收益率的标准差为0.167,二者之间的相关系数为0.40,消费增长与股票市场收益率的协方差为0.002 4。按照CCAPM模型,美国代表性投资者的相对风险规避系数应该为25(0.06/0.024)时,才能解释股票市场的超额报酬。但合理的风险规避系数一般在3左右,这就产生了著名的“股票溢酬之谜”。较大的股票升水难以符合家庭最优化决策,因此,“股票溢酬之谜”引发了大量的研究,许多学者从不同的角度,如:习惯形成[5](P3009-3063)[6](P67-70)、消费财富比[7](P28-36)[8](P35-39)、市场摩擦[9](P97-112)[10](P771-792)[11](P161)、长期风险[12](P52-69)、巨大灾难[13](P823-866)及市场结构[14](P145-158)等方面,进行了实证研究并提出不同解释。而胡召平[15](P51-58)从效用成本的角度对股权溢价之谜进行解释,认为基于资产的风险效用成本是导致股权溢价的主要原因。朱小能等[16](P1-12)认为生产—现金流贝塔可以较好地解释中国股市股票溢价的差异。但相关的研究均没有从我国资本市场的本质特征出发进行研究,因此本文尝试将我国资本市场划分为“牛市”“熊市”和“震荡市”3个具有典型中国股市特点的市场,对“股票溢酬之谜”进行实证检验。

自 20 世纪 90 年代初我国建立股票市场以来,三十多年来取得飞速发展。从1991年底只有14支上市股票,流通市值仅109.19亿元,发展到 2022 年12月30日,我国A股上市公司已达到5 067家,沪深两市总市值为87.75万亿元①,股票市场已经成为我国企业进行融资的重要场所,同时也成为投资者进行投资的一个非常重要的渠道。经过三十多年的长足发展,我国股票市场在为企业筹集资金、降低企业资本成本、分散风险以及提高居民投资收益等方面发挥着越来越重要的作用。但由于我国股票市场的主要定位是“为企业融资提供便利”,加之众多上市公司不具有长期稳定盈利的能力,以及中国股民普遍不具备长期投资的理念,致使中国资本市场无法给投资者带来长期稳定的收益率。研究者们以1990年底刚刚成立的上证指数100点为基础,计算出中国A股市场截止2021年的年化平均回报率为12%,这和纳斯达克的年化回报率相当。但由此计算结果就认为中国股票市场可以给投资者带来长期稳定的超额收益率,是值得商榷的。因为上证指数从1990年12月19日刚刚成立时的100点快速涨到1992年5月21日的1 429.01点,在这一年半的时间里涨幅高达13.29倍,而在这个阶段参与股票交易的投资者寥寥无几,且股票总体的交易额规模也非常小,和现在每天动辄万亿元的交易额相比,1991年全年的交易额仅是现在每天交易额的几十分之一。因此,要计算A股上证指数的年化收益率,应该以1992年5月的1 400为起始点,截止2022年6月底上证指数为3 398点,年化收益率仅为2.99%,和一年期的存款利率(无风险收益率)相当。由此可以看出,我国股市不存在超额收益率。

本文在对消费资本资产定价模型所产生的“股票溢酬之谜”进行理论分析的基础上,利用A股上市公司2013年7月1日至2022年6月30日的月度数据,将我国资本市场划分为“牛市”“熊市”和“震荡市”3个具有典型中国股市特点的市场,并对此进行了实证检验。鉴于我国农村居民因收入偏低无法通过消费与投资的选择来影响资产收益率,利用城镇居民人均消费支出替代全国人均消费支出来构建一个完全市场框架,从而探索“股票溢酬之谜”。

二、理论分析框架

假设一个代表性的消费者在t时刻的投资只有两种资产:一是风险资产Dt,二是无风险资产Ft,其在t时刻的总资产为Vt,无风险资产的收益率是固定不变的rf,而风险资产在t时刻的价格为Pt,服从如下的几何布朗运动:dPt/Pt=μdt+σdωt,其中,ωt是标准的布朗运动,μ是单位时间内风险资产收益率的均值,σ是单位时间内风险资产收益率的标准差。令α为消费者将其全部的储蓄投资于风险资产的比例,则消费者通过选择最优的资产组合使得其终生效用的贴现值最大化。

(1)

s.t.Vt+1=Dt+1+Ft+1=Rt+1(Dt+Yt-

St-Ct)+Ft+St,

dV=[rfVt-Ct+(μ-rf)αVt]dt+

σαVtdωt,

其中,Rt+1为从t期到t+1期消费者风险投资总的回报率。β为消费的贴现因子,E0为条件期望算子,消费者的劳动收入为Yt,消费者的消费水平为Ct。采用随机动态规划求解消费-资产组合投资问题,可以定义值函数为

(2)

那么最优化一阶条件意味着即期消费减少导致的边际效用损失等于未来消费增加所带来的边际效用收益。

U′(Ct)=Et[(βα(1+Ri,t+1)U′(Ct+1)]。

(3)

将式(3)两边除以U′(Ct)得:

(4)

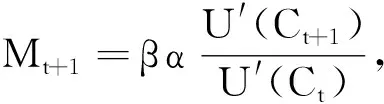
1=Et[(1+Ri,t+1)Mt+1]。

(5)

由于Et[(1+Ri,t+1)Mt+1]=Et(1+Ri,t+1)Et(Mt+1)+Cov[(1+Ri,t+1),Mt+1],则可将式(5)写为

(6)

式(6)对于无风险收益率也是成立的,由于无风险收益率与随机贴现因子之间不存在相关性,故Cov[(1+Rf),Mt+1]=0,从而式(6)可写为

(7)

将式(7)代入式(6)得:

1+Et(Ri,t+1)=(1+Rf,t+1){1-

Cov[(1+Ri,t+1),Mt+1]}。

(8)

在式(8)的两边都减去无风险利率得:

Et[Ri,t+1-Rf,t+1)=-(1+Rf,t+1)×

Cov[(1+Ri,t+1),Mt+1]。

(9)

式(9)表明当随机贴现因子较大时,消费者更倾向于减少本期的消费支出进行投资,从而增加未来的消费支出。

假设收益的对数(ln (1+Ri,t+1))和随机贴现因子的对数(lnMt+1)服从正态分布,并利用定理:若X:N(μ,σ2),则Eexp(X)=Eexp(μ+σ2/2)。

Et[(1+Ri,t+1)Mt+1]=Etexp[ln (1+Ri,t+1)+lnMt+1]=expEt{[ln (1+Ri,t+1)+lnMt+1]+0.5var[ln (1+Ri,t+1)+lnMt+1]}。

(10)

把式(10)代入式(5),并两边同时求对数,式(10)可写为

0=Etln (1+Ri,t+1)+EtlnMt+1+

0.5var[ln (1+Ri,t+1)+lnMt+1]。

(11)

利用公式var(X+Y)=var(X)+var(Y)+2Cov(X,Y),为了简便起见用小写字母表示相应指标的对数值,式(10)可以写为

0=Etri,t+1+Etmt+1+0.5[var(ri,t+1)+

var(mt+1)+2Cov(ri,t+1,mt+1)]。

(12)

由于无风险收益率的方差为0,由式(12)可得:

0=Etri,t+1+Etmt+1+0.5var(mt+1)。

(13)

利用式(12)与式(13)整理得:

Et[ri,t+1-rf,t+1]+0.5var(ri,t+1)=

-Cov(ri,t+1,mt+1)。

(14)

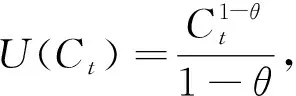
(15)

因此式(5)可以写为

(16)

对式(15)两边取对数,且用小写字母表示相应指标的对数值,可得:

mt+1=lnβ-θVct+1,

(17)

其中,Vct+1=lnCt+1-lnCt。

把式(17)代入式(12)进行化简可得:

0=Etri,t+1+lnβ-θEt[Vct+1]+0.5[var(ri,t+1)+θ2var(Vct+1)-2θCov(ri,t+1,Vct+1)]。

(18)

同理对于无风险收益率rf,t+1为

0=rf,t+1+lnβ-θEt[Vct+1]+

0.5θ2var(Vct+1)。

(19)

利用式(18)和式(19)可得:

Et[ri,t+1-rf,t+1]+0.5var(ri,t+1)=

θCov(ri,t+1,Vct+1)。

(20)

式(20)表明风险资产的期望对数收益率的升水与该资产的对数收益率和对数消费支出增长率的协方差成线性关系,而此协方差往往被称为消费贝塔。

消费资产定价模型将居民消费与投资选择结合起来,研究投资者最大化效用下的投资行为。该模型的成立意味着资产收益与居民消费支出增长间不仅存在着由财富效应造成的单向影响,以居民财产配置选择为主体的消费与投资行为也会引发资本市场中资产收益的波动。

三、实证分析

(一)检验方法

利用广义矩法(GMM)检验标准CCAPM的欧拉方程,GMM检验中的工具变量1包括常数、滞后消费支出增长率(Ct/Ct-1,Ct-1/Ct-2)、滞后利率以及滞后股票收益率。工具变量2包括常数、滞后消费支出增长率(Ct-1/Ct-2,Ct-2/Ct-3)、滞后利率以及滞后股票收益率。运用EVIEWS对β,θ进行直接估计, 其中J- 统计量的自由度为22。

(二)数据来源及处理

实证数据选取的时间为2013年7月至 2022年6月(共 108个月)的月度数据。由于我国资本市场属于典型的资金推动型股市,容易表现出“大起大落”,在资金疯狂涌入股市时,股价表现为持续快速上涨,而当资金离开股市时,股价又常常出现连续暴跌,且投资者在不同的股市周期表现的行为具有较大差异。故本文在进行实证检验时,将时间段分为 “牛市”阶段(2013年7月—2015年6月)、“熊市”阶段(2015年7月—2018年12月)和“震荡市”阶段(2019年1月—2022年6月),这样得出的实证结果更具有实际意义。各数据来源及处理方法如下。

1.股票收益率。我国资本市场成立的时间较短,个股股票价格波动较为剧烈,因此采用上证指数月度加权平均收益率作为股票收益率,数据来源于华安证券系统。

2.无风险收益率。通常选取政府发行的6个月短期国债收益率作为无风险收益率。由于我国发行的主要是中长期国债,短期国债较少,因此选取6个月银行存款利率作为无风险收益率。由于我国银行违约风险较小,且利率市场化程度较低,所以将6个月银行存款利率转换为月度利率作为无风险收益率。

3.消费支出增长率。运用城镇商品零售总额除以城镇月度人口得到城镇人均月度消费额。将1993年1月的价格指数设定为100,作为基准月。利用居民消费价格指数(CPI)的月度数据对消费数据进行调整后得到实际城镇居民人均月度消费额,再根据人均月度消费额计算得出环比月度消费支出增长率。数据来源于国家统计局网站。

表1为2013年7月至2022年6月我国股票收益率及消费支出增长情况。表2为3个子时间段的增长情况。

表1 我国股票收益率及消费支出增长情况 (2013.7—2022.6整个时间段) %

从表2可以看出,由于近年来我国实行宽松的货币政策,无风险收益率逐步走低,而股票收益率在不同区间波动较为激烈,2013年7月至2015年 6月,上证股指从1 946.37点迅速上升到4 277.22点,两年涨幅高达119.78%,呈现出典型的“牛市”特征;2015年7月至2018年 12月,上证股指从4 277.22点快速下跌到2 493.90点,将前两年历经的“牛市”涨幅抹去77%,跌幅达到了41.71%,呈现出典型的“熊市”特征;2019年1月至2022年 6月,上证股指在2 493.90～3 731.49点反复震荡,呈现出典型的“震荡市”特征。

表2 我国股票收益率及消费支出增长情况 (3个子时间段) %

通过比较表1和表2可以发现,2013年7月至2022年6月整个阶段和3个子阶段的股票收益率相比,整个阶段的收益率更平滑,整个阶段的年化收益率和溢酬率分别为4.22%和2.28%。但这看起来比较合理的数据掩盖了股市暴涨暴跌给投资者带来巨大损失的本质。2013年1月至2015年 6月年化股票收益率和溢酬率分别为38.59%和35.69%,体现了在“牛市”中的极高回报率。这只是从指数整体而言,具体到个体投资者,在“牛市”中不赚钱甚至亏损的人也比比皆是。而2015年7月至2018年 12月年化股票收益率和溢酬率分别为-19.42%和-21.19%,平均每个投资者亏损17.8万元,体现了在“熊市”中的巨大亏损效应。在“牛熊”市下,收益率的波动极大。

(三)实证结果与分析

模型估计结果见表3、表4。

表3 CCAPM模型的GMM估计结果(2013.7—2022.6整个时间段)

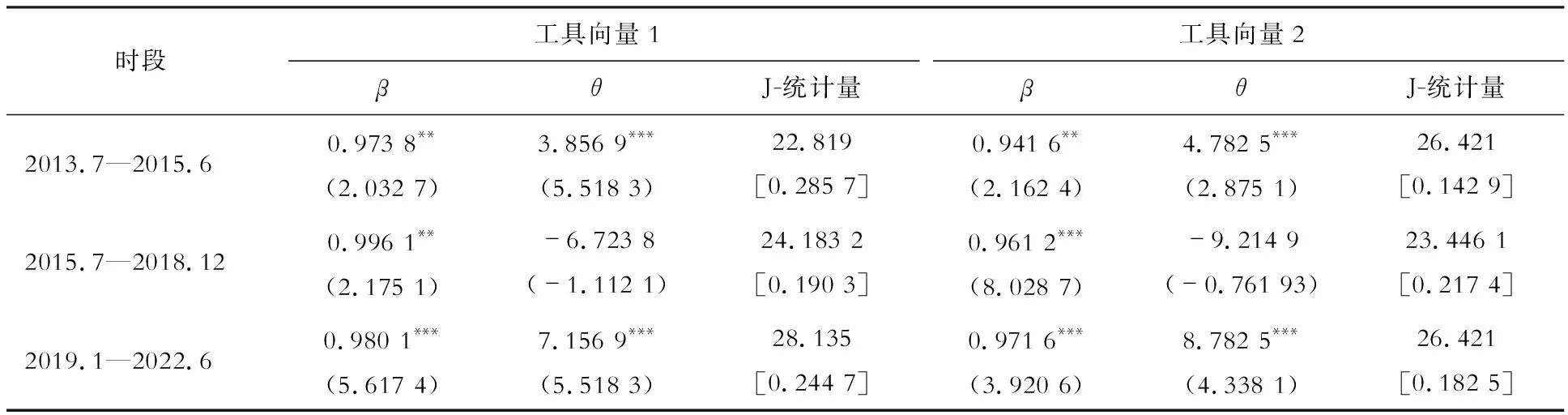
表4 CCAPM模型的GMM估计结果(3个子时间段)

由表3和表4可以看出,2013年7月至2022年6月整个时间段的θ值明显高于3个子阶段,表明利用较长时期(包括了完整的牛熊市)的数据得出的结论是我国资本市场更倾向于存在“股票溢酬之谜”。这是由于较长的时期自动平滑了股市暴涨暴跌的实质,因此得出的结论不具有实际意义。2013年7月至2022年6月整个时间段的年化溢酬率为2.28%。但在实际中,我国股市中存在“1赚2平7亏”的现象,90%的投资者无法在股市中获取稳定的收益,反而是绝大多数投资者在股市中亏损严重。

由表4 可知,在“牛市”和“震荡市”阶段,用不同的工具向量得到的效用折现因子β的估计值为0.941 6～0.996 1,取值符合理论预期,且在 1%或5%的显著性水平下通过检验;相对风险规避系数的估计值为3.856 9～8.782 5,且均在 1%的显著性水平下通过检验。其中使用 2019年 1 月至2022年6月的数据得到的θ估计值有所上升,这可能是由于:一方面,在这个阶段股市市值及交易规模日趋扩大,股市的波动趋于缓和,属于震荡中小幅上升的态势。另一方面,机构投资者增加,个人投资者风险意识上升,投机氛围有所下降。但较低的θ估计值再次证实了我国资本市场并不存在标准消费资本资产模型所带来的“股票溢酬之谜”。“股票溢酬之谜”的本质是股票市场可以给投资者带来长期稳定的超额回报,如,美国道琼斯指数近40年的年化平均收益率为8.6%,纳斯达克指数近40年的年化平均回报率为11.8%。而我国股市出现如此明显与欧美发达市场不同特征的原因是,中国股市的主要功能是“为企业融资”,股指的涨跌主要受到不同时段进入股市资金的多寡影响,且一旦股市行情转暖出现赚钱效应,就会对中小散户形成“吸引”效应,从而使得更多的资金进入股市,推动股指快速暴涨。而一旦行情转冷,各路资金又纷纷杀跌,从而出现短期内股票纷纷出现“跌停板”式的“踩踏”现象,导致股市在短时间内出现暴跌。“追涨杀跌”不仅不能给投资者带来稳定的回报,反而给投资者带来巨大的亏损。θ的估计值在2015年7月至2018年12月的“熊市”出现了不符合模型设定的负值,θ估计值出现负值表明在模型假设中投资者由一个风险规避者变为了一个风险追逐者。从前面的分析可以看出,我国股票市场存在着典型的“牛熊”市特征,股市暴涨暴跌使得资本市场出现混乱,最终导致模型估计结果在“熊市”出现了与预期相反的现象。另外,可以看到参数估计不显著,表明估计值不可信,模型在2015年7月至2018年12月“熊市”的检验结果无法很好地解释我国股票市场出现的异常现象。同时通过计算得出的消费跨期替代弹性估计值为2.146 8～2.876 2,该数值远远大于欧美等成熟资本市场所估计出的消费跨期替代弹性。消费跨期替代弹性高,表明消费者会选择较少的当期消费支出、更多的储蓄,这也与我国居民偏好银行存款、居民储蓄率高的事实相一致。

四、研究结论及启示

本文对标准的消费资本资产定价模型(CCAPM) 进行了实证检验,结果表明,我国投资者的相对风险规避系数远小于成熟资本市场,同时实证结果也不支持我国资本市场上存在“股票溢酬之谜”。我国不成熟的股票市场以及我国居民投资者具有典型的“厌恶损失实现”和“落袋为安”的心理是主要的客观原因。该结果与目前利用我国资本市场数据验证“股票溢酬之谜”的结论基本一致,但本文基于“牛市”“熊市”和“震荡市”3个具有典型中国股市特色的阶段,探索“股票溢酬之谜”,所得出的结论更具有针对性和现实性。

“股票溢酬”从本质上来说是规范的资本市场对投资者风险承受的一种额外补偿,为了促进我国资本市场健康发展,应该建立起长期规范的制度,更加合理地引导居民理性投资股票市场,像欧美等发达资本市场一样能够给予投资者“股票溢酬”,真正起到市场资源优化配置、投资资产保值增值的作用。

实证研究得出我国投资者具有较低的相对风险规避系数,这表明:一方面,由于我国股票市场IPO和监管等制度的不完善,上市公司信息的极度不对称导致内幕交易普遍存在,以及由于资本市场上的交易者长期处于非理性投资状态,股价受到机构和游资操纵严重,典型的“牛熊”市场格局明显,投资者很难在股票市场获取稳定的收益,这也是我国资本市场的一个重要特点。同时,由于我国居民投资渠道狭窄,客观上也加剧了资本市场上股票发行价和交易价格的 “虚高”,从而导致我国投资者投资股票的收益率长期处于低位水平。另一方面,由于我国改革开放后经济持续高速增长,使得居民消费支出的增长速度在过去的十几年间一直高于发达国家。这些典型的新兴经济体的市场特征与欧美等发达资本市场的经济背景有显著的差异,导致了在我国资本市场上不存在“股票溢酬之谜”。这也说明我国证券市场与成熟资本市场相比仍存在差距,特别是在为居民提供长期稳定的投资渠道和投资收益回报方面,差距更为明显。

因此,首先,必须加强资本市场的制度建设,进一步完善我国资本市场的IPO、监管及信息公开等制度,切实实行退市机制,形成“优胜劣汰”的市场生态,让上市公司在资本市场真正能做到“有进有退”,从而提高上市公司的质量;加大对上市公司财务作假的惩处力度,提高其违法成本,使其在违规行为上不敢为、不能为、不想为。其次,上市公司要提高资产质量,扩大资产规模,提升盈利能力和发展能力,增强市场抗风险能力,提高股利支付率,以加大对股东长期持股的回报。最后,加强对投资者的理财教育,引导投资者形成正确的风险防范意识,树立正确的投资理念,坚持长期投资,促进居民财富保值增值,推进经济持续稳健发展。

注 释：

①数据来源:同花顺财经网,2022中国资本市场报告,http://stock.10jqka.com.cn/20221231/c643983740.shtml,2022-12-31。