基于大数据的纯电动客车动力电池安全风险多维度评价

俞蒋彬， 张 欣， 张永涛， 常 亮

（北京交通大学 机械与电子控制工程学院，北京 100044）

新能源电动汽车因其在减少碳排放、降低化石能源消耗和推动电气化交通运输发展等方面发挥重要作用，其产业规模迅速增长，总体发展形势向好［1］.动力电池在使用过程中不可避免的性能衰退会导致车辆运行安全隐患增大，准确评价和预测动力电池安全风险情况是提升电动汽车的安全性、可靠性的重要保证［2］.研究人员从故障触发机制、特征指标变化、反应机理等方面进行了大量探索，形成了初步的理论体系和解决方案［3-4］.然而，在电动汽车实际运行过程中，工况复杂交变，在试验条件下所建立的安全风险评价机制难以应对实车工况下多因素耦合的情况.

随着新能源汽车国家监测与管理平台的建立与发展，大数据技术以其实时性、全局性等优势在车用动力电池系统安全风险预测预警上展现出良好的应用前景.因此，基于电动汽车运行数据，建立大数据视角下的故障风险预测和预警，是目前车用动力电池安全风险领域的热点［5-6］.

何淑波等［7］采用样本卷积和交互神经网络算法实现动力电池关键状态预测，再利用多分类随机森林算法，对动力电池1 min 后的安全风险进行分级预警，经过数据验证该方法的查准率为84%.刘伟霞等［8］对动力电池的5 个维度分别建立风险评估算法并进行线性融合，通过大数据训练算法参数，经过实车验证，该算法提前7 min 预警了电池的热失控.宗磊等［9］针对行驶和充电2 个工况确定了不同电池荷电状态（State of Charge，SOC）、不同温度、不同充放电倍率的电压极差阈值.Hong 等［10］采用改进香农熵和样本熵2 种熵对实车监测和故障报警数据进行分析.研究表明改进的香农熵能够检测出电压异常的单体电池，并有效预测电压异常发生的时间和地点且计算量相对较少.Jia 等［11］搭建卷积神经网络预测模型，经过大数据训练，该模型可以快速准确地预测锂电池在各种工作条件下的短路电阻，平均绝对相对误差为6.75%±2.8%.Jia 等［12］采用专家启发算法、逻辑分类、近邻算法、支持向量机、决策树、随机森林6 个机器学习算法对电池的安全风险进行分类预测，其中支持向量机、决策树、随机森林3 个算法表现出了不错的分类效果.

综上，目前的评价方法主要集中在动力电池的单一维度（温度、电压等）且预警时间较短.本文依托于2022 年数字汽车大赛提供的数据集，提出一种基于大数据的纯电客车动力电池安全风险多维度评价方法.采用多源数据融合处理，得到用于表征电池运行状态的参数，并采用机器学习方法，实现对动力电池的分等级故障预测，最终构建具有动态性、系统性的多维度评价体系，实现了对纯电客车动力电池的多维度安全风险评价.

1 实车运行数据处理

2022 年数字汽车大赛官方所提供的数据是通过国家新能源汽车国家监测与管理平台采集的某品牌10 辆纯电动客车的实车运行数据，10 辆车均在城市内运行，没有固定的路线.每辆车各采集了时间跨度为6 个月的运行数据，采样间隔为10 s.车辆运行特征覆盖长期搁置再行驶、一直行驶、先行驶再搁置等典型用户使用特征，车辆运行环境覆盖全天24 小时以及全年12 个月，具有充分的多样性和广泛性.数据集共计32 个数据采集字段.将数据进行如下的初步处理：①结合文献［13］对数据字段的解释，提取与动力电池相关的20个数据字段，如表1所示.② 偏移处理.在数据矩阵中，部分数据如电压、温度在数据存储和传递过程时为无符号整型，需要进行偏移处理，转化为标准单位下的数值.③ 二次解码.在数据矩阵中，通用报警数据字段采用32 位二进制对通用故障进行编码，其中低19 位有效，其他预留.通过二次解码将通用报警数据转化为19列的故障矩阵.

表1 保留的数据字段Tab.1 Reserved data

数据初步处理完成后，将数据字段划分为数值数据（如电流、电压、温度），状态数据（如充电状态、车辆状态）和故障数据（19 列的故障矩阵）3 类，通过逐一验证各类数据的自洽性，检查不同来源数据之间是否存在矛盾，核实数据反映情况与故障信息是否相符，逐层深入进行数据清洗，数据清洗流程如图1所示.

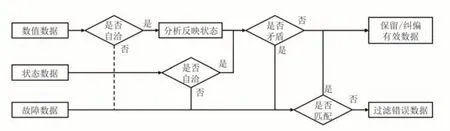
图1 数据清洗流程图Fig.1 Data cleaning flow chart

经过数据清洗，最终获得约510 万条有效数据.为了便于对动力电池故障进行不同角度的研究，对数据进行切分.切分形式包括针对行驶累计里程切分、针对时间维度切分、针对故障等级切分3 种.

1.1 电池包容量估计和SOH 指标计算

电池的性能衰减是电池内部各种失效过程综合作用的结果.电池内部物理化学性质的变化造成了电池外部性能特征的衰减，其主要表现包括开路电压特性变化、电池可用容量减少、电池内阻的增加［14］.本文以动力电池的剩余容量作为电池健康状态（State of Health，SOH）的表征指标，因此需要对动力电池的容量进行估计.

车辆充电通常采用恒流充电，电流几乎稳定，结合时间变化可以对每一时间间隔内的充电容量进行计算.因此，本文以充电片段的电流和时间变化来估算电池组在某时段内的容量增量，并进一步计算得到电池当前最大容量.计算式为

式中：It为t时刻电流大小，A；t0、t1分别为恒流充电片段始、末时刻，Δt为时间间隔，s；SOC0、SOC1分别为恒流充电片段始、末的电池荷电状态，%.根据式（1）估算10 辆车的不同时间的容量，估算散点图如图2 所示.图中不同颜色的散点代表不同编号车辆的容量估算结果.

图2 不同车辆容量估计结果Fig.2 Different vehicle capacity estimation results

图2 中展示了3 个车辆的电池容量变化的线性趋势线，其中数据按时间排序，估算次数越多，使用时间越长.可以发现随着使用时间的增加，车辆的动力电池最大容量逐渐降低，符合客观规律，因此容量估算结果基本合理，能作为SOH 表征指标.

进一步通过分析发现LB47 号车辆累计里程最短，则电池健康状态应较好，可以将其作为初始容量估计的车辆.LB47 号车估算容量的平均值为146.48 Ah，考虑到存在89 km 的累计里程，本文将电池标准的健康容量值设置为150 Ah，并以此计算电池的SOH，计算式为

式中：SOH 为电池健康状态，%；Cmax为当前电池最大容量，Ah；Cfresh为电池初始的最大容量，值为150 Ah.

1.2 单体电池内阻估计和内阻一致性指标计算

根据混合脉冲能力特性（Hybrid Pulse Power Characteristic，HPPC）测试结果表明，内阻在低SOC 区间和高SOC 区间的变化较大［15］，在中部SOC 区间（40%~80%）保持相对稳定，可视作定值［16］.因此，在中部SOC 区间，恒流充电片段中电流切换处估算得到的阻值可基本代表电池内阻的平均水平.计算式为

公式中：Ri表示第i个单体的内阻，mΩ；Ui-A、Ui-B表示充电过程中电流切换前、后第i个单体的电压，V；IA、IB表示充电过程中电流切换前、后的最后时刻的电流，A.根据式（3）估算10 辆车的单体电池内阻，估算散点图如图3 所示.

图3 不同车辆电池内阻估计结果Fig.3 Different vehicle internal resistance estimation results

图3 展示了3 个车辆电池内阻阻值变化的线性趋势，可以发现随着使用时间的增加，动力电池的内阻阻值增加，符合客观规律，因此内阻估算结果合理，可以用于后续电池安全风险评价.

在得到单体电池内阻后，为表征电池的内阻一致性，计算单体电池内阻极差和单体电池内阻标准差，计算式分别为

式中：ΔR表示单体电池内阻极差，mΩ；Rmax和Rmin分别表示电阻的最大值和最小值，mΩ；Rˉ为单体电池内阻的平均阻值，mΩ；N1为单体电池个数；SR表示单体电池内阻的标准差，mΩ.

1.3 电池温度相关指标计算

数据字段中与温度相关的信息包括最高温度、最低温度、单体电池温度列表.为表征电池的运行温度状况和温度一致性，可以通过计算获得固定时刻下的单体电池温度极差、单体电池温度平均值、单体电池温度标准差以及最大单体电池温度变化率.对应的计算式分别为

式中：ΔT表示温度极差，℃；Tmax和Tmin分别表示温度的最大值和最小值，℃；Tˉ表示温度平均值，℃；Ti表示第i个监测点温度，℃；Tt，i表示t时刻第i个检测点的温度，℃；N2表示温度探针总数；ST表示温度标准差，℃；ROCT表示最大的温度变化率，（℃/s）；Δt表示采样时间间隔，s.

1.4 电池电压相关指标计算

数据集中与电压相关的有效信息包括总电压、单体最高电压、单体最低电压、单体电池电压列表.为表征电池的运行电压状况和电压一致性，可以通过计算获得固定时刻下的单体电池电压极差、单体电池电压平均值、单体电池电压标准差以及非正常电压电池占比.对应的计算式分别为

式中：ΔU表示单体电池电压极差，V；Umax和Umin分别表示电压的最大值和最小值，V；Uˉ表示单体电池电压平均值，V；Ui表示第i个单体电池电压，V；SU表示电压标准差，V；PoutU表示超出正常电压范围的电池的数量占比；NoverU表示高于正常电压范围的单体电池个数，NunderU表示低于正常电压范围的单体电池个数.

2 动力电池故障等级预测算法

为确保故障等级预测的及时性和准确性，本文采用机器学习方法对电池故障状态进行预测.将电池故障预测视为多分类问题，通过相关性分析选取合适的算法输入，最终输出预测的风险等级.经过对电池故障等级统计，发现数据集中电池各个故障等级的数量分布不均，这限制了神经网络等要求样本分布均匀的算法应用.因此本文拟采用决策树、随机森林以及近邻算法（K-Nearest Neighbor，KNN）3 个算法进行故障等级预测.

综合考虑预测效果和面对故障采取应对措施需要的时间，本文设定30 min 的预测时长，根据数据切分结果，提取有故障信息、故障前30 min 以及正常行驶的数据条目共计约32 万条数据，作为数据集，并按照7∶3 的比例将数据划分成训练集和测试集，对算法采用十折交叉验证.算法构建流程如图4所示.

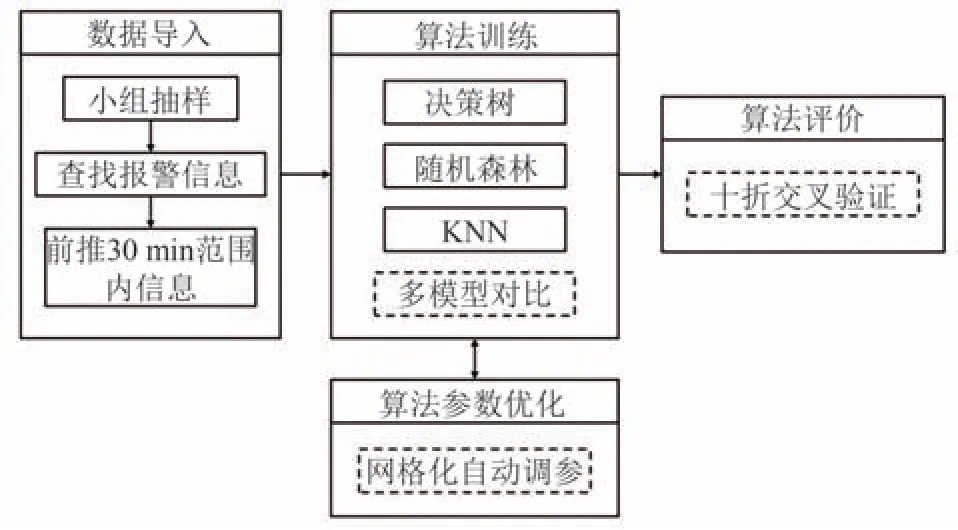
图4 电池故障等级预测算法构建示意图Fig.4 Schematic diagram of battery fault grade prediction algorithm construction

算法参数优化中，不同算法需要优化不同的参数.决策树算法需要优化最大深度、节点可分最小样本数和叶子节点所含最小样本数3 个参数.随机森林算法需要优化决策树数量、树最大深度、节点可分最小样本数和叶子节点所含最小样本数4 个参数.KNN 算法需要优化最近样本数量1 个参数.

2.1 基于相关性分析的算法输入确定

考虑到数据中存在非偏序关系参数如车辆运行状态、充电状态等，本文采用Spearman 秩相关系数进行相关性分析，并对非偏序关系参数采用one-hot编码，保证相关性计算结果的合理性.相关性计算结果如图5 所示.

图5 参数Spearman 秩相关系数热力图Fig.5 Parameter Spearman rank correlation coefficient heat map

最终选取电池包SOH、SOC，最大电阻差，最大温度差，温度标准差，最大电压差，电压标准差，最大、最小温度，最大、最小电压，绝缘阻值和累计里程共计 13 个参数作为算法训练的输入.

2.2 基于性能指标的算法优选

经过网格化自动调参，3 种算法均达到当前最优.不同算法对不同故障等级的预测效果性能指标如表2 所示.其中一级故障指不影响车辆正常行驶的故障，二级故障指影响车辆性能、需要驾驶员限制行驶的故障，三级故障指驾驶员应立即停车处理或请求救援的故障［13］.

表2 3 种算法对不同故障等级的预测效果Tab.2 Prediction effect of three algorithms on different fault grade

通过对比不同算法对不同故障等级预测的性能指标，发现对于无故障、一级故障、二级故障3 种状态，3 种算法均显示出较好的效果.对于三级故障，3 种算法效果没有预测其他几种故障等级时优异，这与三级故障的样本数量较少有关.

综合比较发现随机森林算法，其预测效果综合优于其他算法，同时在运算速度上，本文中的随机森林算法依赖2.59 GHz 的CPU 运算，每组数据耗时5.6 ms，这与30 min 的预测时长相比足够迅速，所以该预测算法的运算速度能够满足及时预测的需求.最终选取随机森林算法作为电池故障等级预测算法.

3 基于AHP-EWM 的电池安全评价

结合数据处理结果和故障等级预测算法，构建了具有5 个维度、14 个指标的电池安全风险评价体系.层次结构如图6 所示.

图6 动力电池多维度安全风险评价层次结构示意图Fig.6 Hierarchical chart of the multi-dimensional safety risk evaluation of power batteries

这5 个维度、14 个指标能够充分体现单体电池状态、单体电池之间交互影响和电池包状态.状态参数类型涵盖电压、温度、电阻.时长涉及实时、短期变化、长期预测.构建的评价体系具备典型性、系统性和动态性特征，能够全面评价电池安全风险.

3.1 数据标准化

为了避免由于不同类型指标量纲和数量级不同，对最终的安全风险评分产生的影响.本文对所有的指标进行了百分制打分处理，使得所有指标均标准化，并采用3σ 多层次筛选算法提取指标的阈值.百分制打分流程如下.

步骤1：利用3σ 多层次筛选算法计算数据集特征阈值.① 对于n维变量X=［x1，x2，…，xi，…，xn］，X服从高斯分布，定义初始变量X0=X，即X0~（μ0，σ0），其中，xi为变量X的第i个取值，μ0为X0均值，σ0为X0标准差.②剔除X0中超出［μ0-3σ0，μ0+3σ0］范围的元素，形成X1，X1中数值满足μ0-3σ0≤≤μ0+3σ（0i∈［1，n］）.③按②迭代计算j次，得到Xj.当满足|μj-μj-1|≤（tt为迭代容差）时，终止迭代.④输出μj+3σj和μj-3σj数值.

步骤2：结合文献［17-18］规定与3σ 多层次筛选算法计算结果，确定阈值.

步骤3：确定0 分和100 分对应的指标数值，中间状态采取线性插值方式打分.

步骤4：对于超出某一指标上、下阈值的，该项指标打分为-1 分，即安全风险总分0 分.

经过标准化处理后的评价指标一定程度上消除了量纲和数量级的影响.同时对超出上下限制的数据采取总分打0 分的方式，有利于提高对可能发生三级故障数据的甄别能力.

3.2 权重矩阵确定

为降低主观因素对权值的影响，本文采用层次分析法和熵权法组合的方法来确定权重矩阵，在发挥各自方法优势的情况下，一定程度上削弱了主观偏差性和客观片面性.

层次分析法（Analytic Hierarchy Process，AHP）可以将专家、决策者的经验引入评价过程［19］.本文采用7 标度对指标进行两两比较，构建比较矩阵，并进一步计算权重矩阵.7 标度法各个标度重要性含义如表3 所示.

表3 不同标度重要性含义Tab.3 Meaning of scale importance

熵权法（Entropy Weight Method，EWM）按照每个指标的信息量确定权重，信息熵可以衡量指标包含的有效信息［20］.熵值越大，说明指标数据之间的变化程度越大，所反映的信息量也越大，其对应的权值也越大.

本文采用层次分析法和熵权法结合确定权重，权重的计算式为

式中：ωj为第j个指标的最终权重；uj为通过层次分析法确定的第j个指标的权重；vj为通过熵权法确定的第j个指标的权重；n为指标总数.最终通过计算，各个指标的权重如表4 所示.

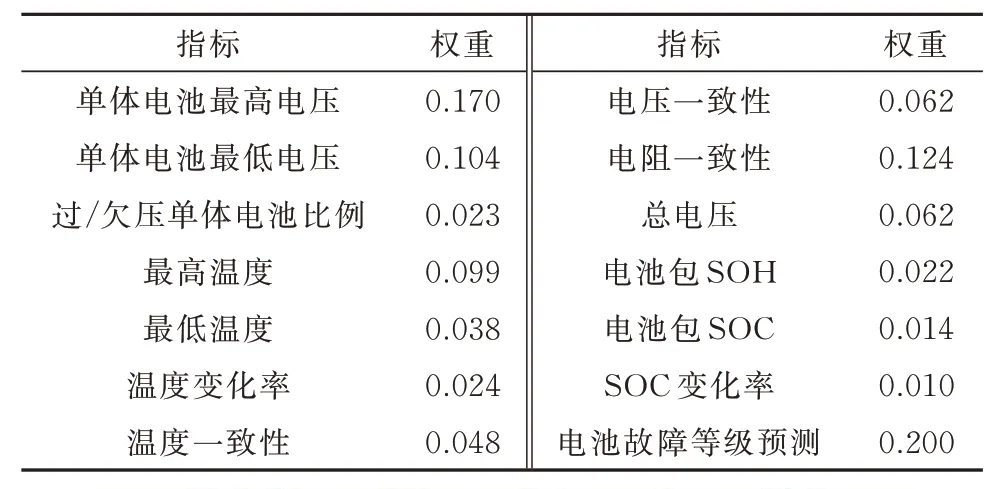
表4 各指标对应权重Tab.4 Each index corresponds to the weight

综上，本文基于多维度安全风险评价体系，对14 项指标进行百分制打分，再将各指标分数乘以对应的权重，最后求和得到对动力电池的安全风险评价分数.对数据集中所有数据进行多维度安全风险评价，统计各个故障不同区间分数的占比情况如图7所示.

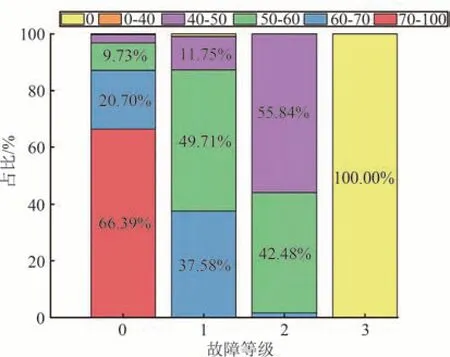
图7 各故障等级评分占比堆积柱状图Fig.7 Accumulation bar chart of the score proportion of each fault

由图7 可知，无故障的评分集中在70 分以上，占比66.39%.一级故障的评分集中在50 分到70 分之间，占比87.29%.二级故障的评分集中在40 分到60 分之间，占比98.32%.三级故障的评分全为0 分，占比100%.分数的集中区间的占比都达到了80%以上，具有一定的代表性，可以通过安全风险评价的分数作为划分安全等级的依据.同时可以发现不同故障等级的分数分布具有一定的层次性，也有利于区别不同等级的故障.

对于存在未在集中分数区间的数据，主要原因有2 个.一是由于实时评价结果容易受到实车数据采集误差的影响，存在部分偶发性的低分.这类数据可通过增加滤波算法或设置故障判定的时间来避免.二是由于算法对故障的提前预测，导致电池的未来安全评分降低，使得安全风险总分降低，分数未在集中分数区间.

4 具体事故应用分析

目前实车所采用的故障检测方法是比对实际运行数据和设定的运行数据正常范围，如果实际运行数据超出正常范围，进行报警.这种方法能够监控的电池状态指标类型较少，只有电压、温度和电流.同时也没有做到提前预警，突然发生故障时留给驾驶员操作和反应的时间不够，不利于妥善处理安全风险问题.本文采用多维度的安全风险评价来对电池进行安全风险评价和故障预警，当电池安全风险评价分数在70 分以上时，视为安全状态，当分数在70~50 之间时，视为一级故障，当分数在60~40 之间时，视为二级故障，对于50~60 这一分数重叠区域，则采用故障预测结果作为故障等级.这种方式能够更好地体现电池安全风险等级的变化情况，并进行提前预测，提高运行安全.本文通过两例具体的故障案例进行分析，来验证本文方案的可行性.

1） 事故1.

编号LB42 的车辆在2020 年4 月11 日，约7 时27 分，故障信息从无故障到三级故障.图8 为应用本文提出的多维度安全风险评价方法后，电池安全风险评价分数和故障等级预测的变化曲线.

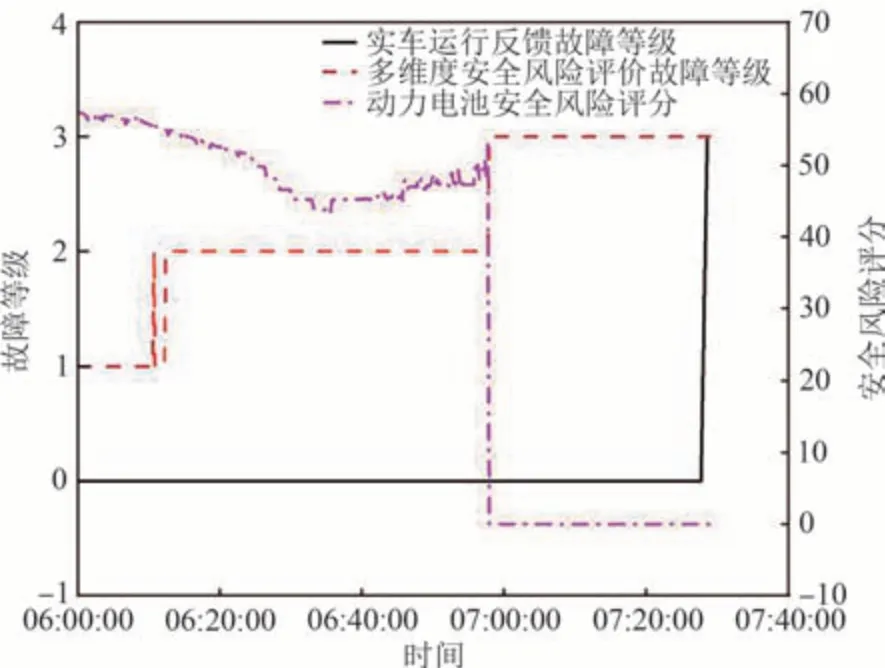
图8 安全风险评价分数和故障等级变化曲线Fig.8 Safety risk evaluation score and fault grade change curves

由图8 可知，电池安全风险评价总分呈下降趋势，中间产生分数上升是由于车辆从熄火状态转换到驱动状态，电池的充放电状态和电流大小更加符合驱动情况下的车辆，导致评分有所升高，但总体评分在40 分到60 分区间，处于二级故障的评分范围.在6：25：00 之前，安全风险评分在50~60 的范围内，根据预测算法的结果，风险等级从一级升到二级，6：57：00 之前安全风险分数在50 分以下，为二级故障，之后则为0 分，为三级故障，多维度安全风险评价得到的故障等级逐渐升高，反映了安全风险在不断升级，相比于实车中突然从无故障到三级故障，更有利于技术人员及驾驶员把握风险情况做出合理的应对措施.同时，本方案向系统报告一级故障的时间，相较于车辆自身报警时间提早约90 min，向系统报告三级故障的时间提早约30 min，避免了故障突发导致技术人员及驾驶人员无法及时做出反应从而引起安全事故.

2） 事故2.

编号为LB79 的车辆在2020 年7 月16 日约17 时42 分报警，故障信息为储能装置欠压.图9 为应用本文提出的多维度安全风险评价方法后，部分相关分指标评分变化的曲线图.

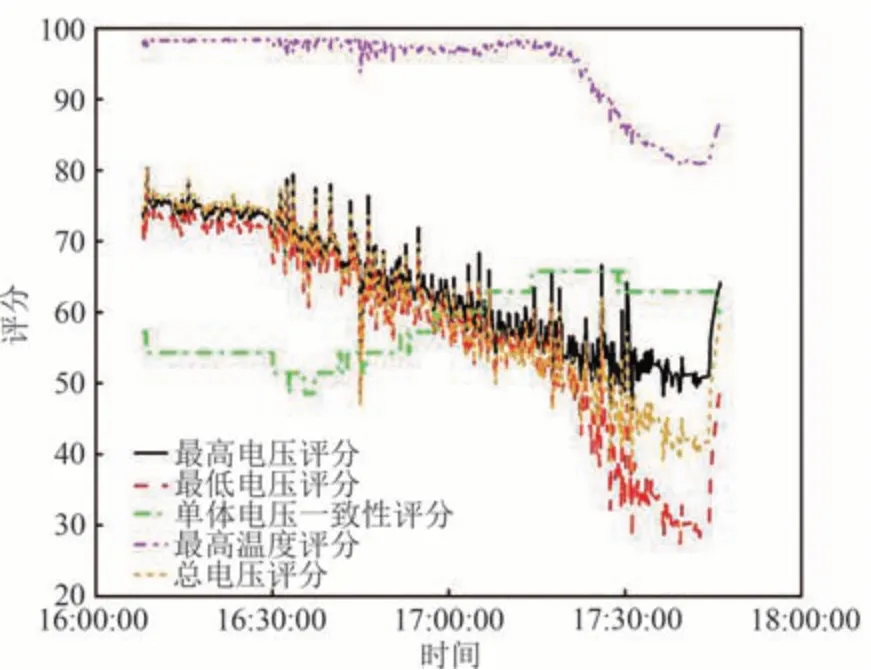
图9 分指标评价分数变化曲线Fig.9 Sub-index evaluation score change curve

由图9 可知，与电压相关的评价指标如最高电压、最低电压、总电压波动幅度很大，整体呈现下降趋势，其中最低电压的评分最低，说明动力电池出现了欠压类型故障，同时电压一致性的评分没有降低的趋势，说明欠压的情况不是出现在小部分动力电池中而是大范围地出现，温度指标变化前期较为平稳，只有在后段呈现下降趋势，推测是由于电压的变化，导致电池产热变化，从而影响温度，说明电池的温度方面并没有出现故障.综上，运用本文的方案，通过分数的大小和变化可以推断出动力电池产生了欠压的故障，相比于单一的故障等级，更加明确地指出了故障的类型.此事故的案例分析说明本文的多维度安全风险评价可以通过分析各指标的评分变化，锁定故障的大致类型，便于技术人员及驾驶员采取相对应的措施.

5 结论

1） 针对目前动力电池安全风险评价维度单一的问题，提出了具有5 个维度、14 个指标的动力电池多维度安全风险评价体系，全面评价动力电池安全风险，通过数据集验证了能够通过分析各个具体指标评分的变化曲线，得到动力电池故障的大致类型.

2） 针对目前电池安全风险预测时间不长的问题，采用机器学习方法预测故障等级.经过性能指标优选，选定了随机森林算法作为故障等级预测算法.可以提前30~90 min 预测故障发生.针对不同的故障等级，本文的预测算法平均预测精准度高达97.25%.

3） 结合数字汽车大赛提供的数据集对方案进行了验证，通过本文的安全风险评价得到的动力电池安全风险分数与原始数据匹配程度高，且分数随着故障等级有层次性.2 个实际安全风险案例的验证结果表明，应用本文的方案能够更早地提示故障的发生，并且能够锁定故障的类型.

本文的方案在预测预警电池安全风险和协助确定电池故障类型上有一定实用价值.但由于本数据集内故障等级和故障类型的数量分布不均匀，在未来可以通过更全面的数据集训练不同的机器学习算法（如神经网络）优化故障预测效果.