高中物理常见“碰撞”模型及其性质分析

王涵

［摘 要］“碰撞”模型是高中物理中十分重要的一类模型，在每年的高考物理题中都会有所涉及。“碰撞”模型中包含诸多问题，每一个模型背后都有着不同的性质，使得学生在解题中具有一定的难度。文章全面、系统地总结了常见“碰撞”模型及其性质，以期为教师引导学生快速解答常见的碰撞类问题提供参考。

［关键词］碰撞；模型；高中物理

［中图分类号］ G633.7 ［文献标识码］  A ［文章编号］ 1674-6058（2023）26-0052-03

“碰撞”作为高中物理中重要的模型之一，在每年的高考物理题中都会出现，除了会出现在选择题中，还会出现在压轴题中。而且在很多情况下，其背景较为隐蔽，学生难以准确发掘，因此解答问题也就较为困难。为了帮助学生快速解答常见的碰撞类问题，笔者结合实际问题，系统性地总结常见题型，分析常见问题。

一、弹性碰撞

（一）一动碰一静

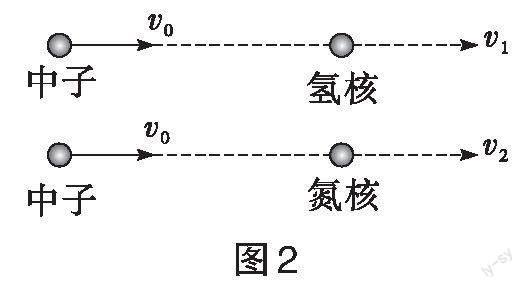
［例1］如图2所示，速度为[v0]的中子与静止的氢核和氮核发生弹性碰撞，碰撞后氢核和氮核速度分别为[v1]和[v2]，则下列说法正确的是（ ）。

[A.]碰撞后，氮核的动量小于氢核

[B.]碰撞后，氮核的动能小于氢核

[C. ][v2>v1]

[D.][ v2>v0]

解析：由题意可知，在碰撞过程中中子、氢核和氮核满足动量守恒和机械能守恒。

综上可得正确选项为[B]。

（二）两动相碰

如图3所示，质量为[m1]、[m2]的小球分别以速度[v1]、[v2]的速度发生弹性碰撞[（v1>v2≠0）]。碰撞后[m1]、[m2]小球以[v′1]、[v′2]速度运动。

静”模型。

不同质量小球碰撞后的运动情况也会有所差异（如表1）。

［例2］质量为[M]的大球和质量为[m]的小球如图4所示进行放置，从高[h]处静止释放，[h]远大于球的半径，忽略空气阻力，则下列说法正确的是（ ）。

[A.]若[M=3m]，则两球碰撞后，小球上升高度为[4h]

[B.]若[M>>m]，小球可无限上升

[C.]若大小球互换位置，且[M=3m]，则小球上升高度为[h]

[D.]若大小球互换位置，且[M=3m]，则大球上升高度为2[h]

二、非弹性碰撞

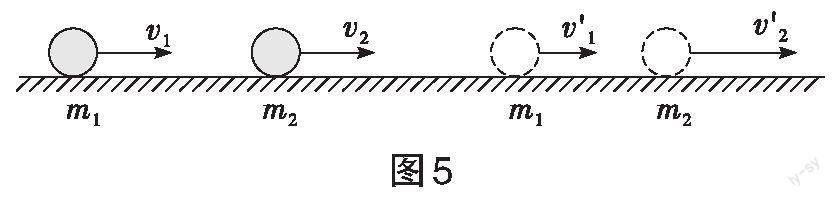
如图5所示，当两物体在发生碰撞后，形状不能完全恢复时，即为非弹性碰撞。此时，碰撞前、后不满足机械能守恒。

［例3］如图7所示，足够长的木板[B]在光滑水平面上，木块[A]放在木板[B]的最左端，[A]、[B]间接触面粗糙，且[mA=mB=m]，初始木块[A]以速度为[v]向右运动，木板[B]速度为[2v]，方向向左，则下列说法正确的是（ ）。

[A.][ A]、[B]最终均静止

[B.][ A]、[B]最终均向左做匀速直线运动

[D.][ A]、[B]减少的动能转化为[A]、[B]摩擦产生的内能

解析：在本题中，木块与木板所构成的系统动

由能量守恒定律可知，[A]、[B]减少的动能转化为[A]、[B]间摩擦产生的内能，则[D]正确。

故正确选项为[B]、[C]、[D。]

三、弹性碰撞和非弹性碰撞的融合

在一些复杂的问题中，往往涉及弹性碰撞和非弹性碰撞两种情况。在解答这类问题时，首先需要学生对过程中的碰撞类型有一个准确的认识，而后结合不同碰撞的特点进行列式计算，进而解答问题。

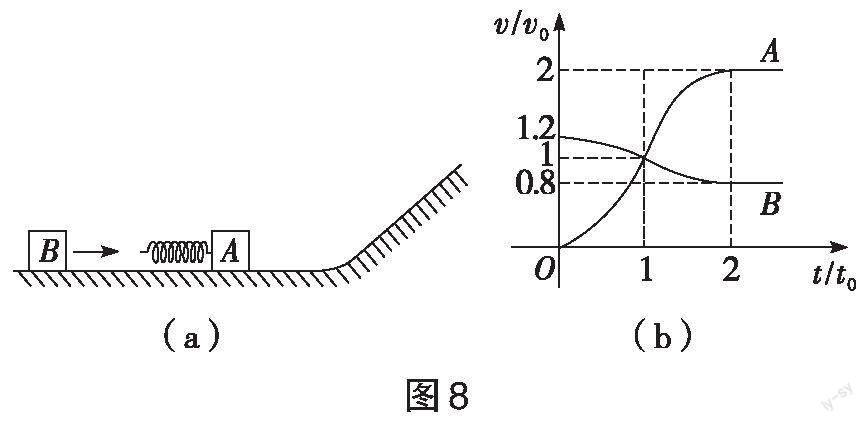
［例4］如图8（a）所示，光滑平面上静止一质量为[m]的物块[A]，与轻质弹簧连接，物块[B]向[A]运动，[t=0]时，与弹簧接触，[t=2t0]时分离，第一次碰撞结束，其[v-t]图像如图8（b）所示，已知[t=0]到[t=t0]时间内，物块[A]的运动距离为[0.36v0t0]。[A]、[B]分离后，[A]滑上粗糙斜面，然后滑下，与[B]再次接触，之后[A]再次上滑，达到的最高点与上次相同。斜面倾角为[θ（sinθ=0.6）]，求：

（1）第一次碰撞中，弹簧的最大弹性势能与最大压缩量；

（2）[A]与斜面的动摩擦因数。

（2）物块[A]第二次到达相同高点，说明第二次分离时，[A]的速度为[2v0]，水平向右。

设[A]第一次滑下斜面的速度大小为[v′A]，向左为

［例5］如图9所示，原本静止在光滑水平面上的小车质量为[M=2 kg]，上表面为光滑曲面，现在有一个质量为[m=1 kg]可视为质点的小球以速度[v0=3 m/s]从左端滑上小车，小球没有翻过曲面，最后从左侧离开。求：

（1）小球离开时，其与小车的速度；

（2）曲面的高度。

即曲面高度应大于等于[0.30 m]。

综上所述，在高中时期，考试中经常遇到的碰撞类问题可以分为弹性碰撞、非弹性碰撞和两者的综合性问题。在实际解答这类问题时，学生一定要准确辨别出问题中的碰撞类型，而后结合不同碰撞模型下的运动特点进行列式计算，从而解答問题。

［   参   考   文   献   ］

［1］  司寿和.摭谈“碰撞类”模型问题的思维认知［J］.中学生理科应试，2023（3）：28-30.

［2］  许文.探究碰撞速度关系 深化碰撞作用模型：碰撞模型的拓展与应用［J］.教学考试，2022（31）：35-38.

［3］  王多平.2022年全国高考乙卷物理压轴题的解法探讨［J］.数理化解题研究，2022（28）：125-127.

［4］  欧其武.动量守恒定律在碰撞类问题中的运用［J］.中学物理教学参考，2022，51（14）：50-52.