基于改进的状态空间模型进化算法的航班优化调度
李 恒,王 嘉
(长沙航空职业技术学院,湖南 长沙 410124)
随着我国经济的快速增长,民用航空业得到了迅速发展,使得机场数量、飞机数量和航班数量不断增加。伴随着空中交通流量的飞速增长,原有的先到先服务(First Come First Service,FCFS)航班调度方法已不能满足我国航空业的发展需求,造成很多大型机场在波峰段航班延误率越来越高,空中交通拥堵现象十分严重。因此,针对航班优化调度问题国内外专家、学者进行了较为深入的研究,他们从优化目标、航班优化调度数学模型、求解算法和空中交通流量管理策略等不同的方向优化,以期解决问题。
潘贺采用人工免疫算法,求解航班优化调度问题,实验结果表明该方法能有效减少进离港航班的延误时间,证明了算法的可行性和鲁棒性[1]。Мahmud 采用花卉授粉算法,求解多跑道协同调度问题,结果表明该方法能减少航班延误损失,提升多跑道协调运行能力[2]。徐兆龙等采用蚁群算法,对多跑道航班协同调度数学模型进行仿真实验,证明了该模型和算法的可行性和有效性[3]。李丹程等采用结合免疫算法和模拟退火算法,求解离港航班调度方法,结合国内某机场的实际数据,对算法进行验证,证明了这两种算法的可行性和有效性[4]。王东兴等把航班着陆调度看作是多目标优化问题,提出了一种吱呀轮SWO( Squeaky-Wheel Optimization)启发式算法,实验结果表明该算法能有效求解该问题[5]。SHI 等提出了CGIC 的启发式算法,将航班调度分解为若干子问题,重新计算了各航班的起降时间,给出了优化的航班序列[6]。虽然上述模型和算法各有所长,但这些模型多是对延误损失和跑道的吞吐量的航班静态调度研究,对单跑道航班调度的总延误时间和航班动态实时调度研究较少。
基于状态空间模型进化算法( Evolutionary Algorithm based on State-space model,SEA)是李茂军等提出的一种新颖的进化算法[7]。符宏艳等应用SEA 算法解决电力市场竞价问题,实验结果表明该算法比遗传算法能更快搜索到最优解[8]。凌哲利用SEA 算法解决轨道交通优化调度问题,通过采用非均匀变异算子的状态进化矩阵,提高了算法的搜索能力和收敛速度[9]。杜佳佳利用SEA算法解决城轨自动运行列车速度优化问题,并取得了良好的效果[10]。虽然SEA 算法能有效解决上述问题,但都是采用实数编码,对于采用序号编码解决组合优化问题(如航班优化调度问题、Flow-shop 问题[11,12]和旅行商问题[13]等)研究较少,因此本文提出一种改进的状态空间模型序号编码进化算法(A modified Order coded Evolutionary Algorithm based on State-space Мodel,МOSEA),并研究其在航班进离港优化调度中的应用。仿真实验表明:这种算法对于解决航班进离港优化调度的航班排序问题是非常有效的。
1 单跑道航班优化调度模型
1.1 目标函数
单跑道航班进离港调度是将某一时间窗内进离港航班看作一个整体,在确保飞机安全的前提下,以航班延误时间和最小安全间隔为约束条件,对进离港航班顺序进行统一优化排序,使得研究时段内机场所有航班总延误时间最少,属于典型的组合优化问题[14]。进离港航班总延误时间目标函数如式(1)所示,其中为进港航班总延误时间,为离港航班总延误时间。
1.2 符号说明
单跑道航班调度模型中会使用到大量符号、变量,相关符号定义如下:
:离港航班集合,
:进港航班集合,
R:平行独立的机场跑道集合,
STAi:航班的实际进港时刻
ETAi:航班的预计进港时刻
AATmax:航班进离港期间,进港航班允许的最大提前时间
STDi:航班的实际离港时刻
ETDi:航班的预计离港时刻
ADTmax:航班进离港期间,离港航班允许的最大提前时间
DATmax:航班进离港期间,进港航班允许的最大延误时间
DDTmax:航班进离港期间,离港航班允许的最大延误时间
:=1,跑道r上有航班进港;=0,跑道r上没有航班进港
:=1,跑道r上有航班离港;=0,跑道r上没有航班离港
:表示时隙s分配给进港航班
:表示时隙s分配给离港航班
C:所有航班的总延误损失
θij:连续两架航班进离港的最小安全间隔
1.3 约束条件
最小安全间隔约束。为保证飞行安全,在同一跑道起降的飞机,须满足式(2)相邻两架航班的最小安全飞行间隔约束,i和j分别表示前机和后机。
进离港航班起降时隙资源约束。式(3)表示每一个进离港航班只有分配到一个起飞降落时隙,才允许进离港降落或起飞。
机场跑道资源约束。为了保证进离港航班的安全,须满足式(4),它表示一条跑道在任意时间内,最多只能有一架起降航班。
进离港航班最大提前时间约束。式(5)、式(6)表示航班优化排序后进离港航班不能超过规定的最大提前时间。
进离港航班最大延误时间约束。式(7)、式(8)表示航班优化排序后进离港航班不能超过规定的最大延误时间。
2 基于改进的状态空间模型序号编码进化算法
2.1 算法简介
遗传算法的编码方式有二进制编码、实数编码和序号编码等不同方式。通过对航班优化调度问题的分析,可知航班优化调度实际是求最优的航班起降序列。若采用二进制编码,则经过交叉操作后会产生无意义的编码,造成解码错乱。若采用十进制对航班序列号进行编码,假设有m个航班,则可能产生m!种航班序列,同样会产生很多无意义的编码,而且还会增加算法的复杂度和运算量。因此,在求解组合优化问题(如航班优化调度问题、旅行商问题和Flow-shop 问题等)时,采用序号编码比用其他几种编码方式更直接、更方便。序号编码遗传算法不能采用常规的交叉算子,因此有学者提出了针对序号编码遗传算法的РOX、JOX、SРX 等特殊交叉算子[11],但这些交叉算子操作较难实现,因此本文提出了一种改进的状态空间模型序号编码进化算法(МOSEA),此算法采用序号编码,不使用交叉算子,只使用变异算子,且通过构造状态进化矩阵等操作来实现变异算子的功能,简化了遗传操作,继承了SEA算法和单亲遗传算法的优点[15]。
2.2 算法的原理
МOSEA 算法采用序号编码方式,不使用交叉算子,通过构造状态进化矩阵来实现基因换位等遗传算子功能,使种群不断地进化,并结合选种池的选择操作实现种群的优胜劣汰。状态空间模型序号编码进化算法表示为离散系统的状态空间模型:
其中X(k)表示第k代群体,G为状态进化矩阵,X'(k+1)表示第k+1 代群体。X(k)是一个N×M的矩阵,此矩阵的各个行向量表示一个个体,即有N个个体,每一个个体包含M个变量。通过进化算法群体中个体之间的信息交换策略来构建状态进化矩阵,并通过构造状态进化矩阵G来改变基因的排序,实现变异算子的功能,保持群体X(k)的多样性并不断地进化。根据离散系统理论,在构造矩阵G时应注意是收敛矩阵或保证矩阵G的特征值在Z平面的单位圆内,否则算法会不收敛。算法步骤:首先是使用序号编码随机生成一组满足约束条件的初始群体X(0),其次构造状态进化矩阵G,按照式(9)进行计算,并左乘矩阵G得到群体X'(1),将X'(1)中不满足约束条件的个体,其适应度赋值为0,之后重新随机生成G,再按照式(9)进行迭代,产生一系列的X'(1),X'(2),X'(3)……把X(k)和满足约束条件的X'(k+1)一起投入选种池,按照优胜劣汰原则,根据适应度值大小,按从大到小的顺序排列,选择前N个适应度值对应的个体构成下一代群体X(k+1),对计算结果进行判断,如果满足结束条件,则输出计算结果。基于状态空间模型序号编码进化算法的闭环模型流程图如图1 所示。
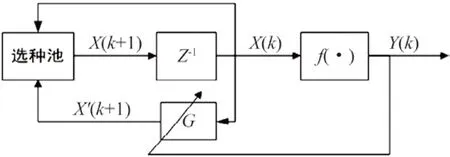
图1 МOSEA 算法流程图
3 单跑道航班进离港优化调度计算步骤
3.1 编码方式
单跑道航班进离港优化调度属于典型的组合优化问题,求解组合优化问题时,采用序号编码比用二进制编码和实数编码等方式更直接、更方便。МOSEA 算法通过构造状态进化矩阵G来实现基因换位等遗传算子功能,使群体不断地进化和保持多样性,并结合选种池的选择操作实现种群的优胜劣汰。具体编码方法如下:
假设X(k)为某一航班序列,其初始航班序列xT(0)={1,2,3,4},状态进化矩阵再进行X'(k+1)=GX(k)的计算,得到新的航班序列xT(1)={2,1,3,4},将xT(1)中不满足约束条件的个体,其适应度赋值为0,按照优胜劣汰、适者生存的进化原则选出优秀个体,形成下一代群体序列,之后重新随机生成再进行X'(k+1)=GX(k)计算,得到另一个新的航班序列xT(2)={2,3,1,4},并依次迭代。
若以10 个航班为例,编码前的初始航班序列如表1 所示,编码后的航班序列如表2 所示。

表1 编码前的初始航班序列

表2 编码后的航班序列
使用上述编码能够确保任意航班序列都对应于一条具有实际意义的航班起降序列,从而有效避免了无效航班序列的产生。此外该编码方式还具有操作简单、无需解码等优点。
3.2 状态进化矩阵的构造
МOSEA 算法的核心是状态进化矩阵,可以通过不同方法来构造状态进化矩阵G。不同的构造方法,算法的求解问题不一样,其搜索速度和效率等性能也有很大影响。比如SEA 算法采用实数编码,通过模拟遗传算法的交叉和变异算子功能来构造状态进化矩阵G,主要用于求解约束优化问题;又如МOSEA 算法采用序号编码,不使用交叉算子,通过模拟遗传算法的变异算子功能来构造状态进化矩阵G,主要用于求解组合优化问题。
МOSEA 算法状态进化矩阵构造方式如式(10)所示,它是一个N×N进化矩阵,矩阵的每一行、每一列有且只有一个元素为1,其余为0。
3.3 新种群的产生
使用序号编码随机生成一组满足约束条件的初始群体X(0),按照离散状态空间模型X'(k+1)=GX(k)进行迭代计算,生成下一代群体X'(k+1),并计算下一代群体X'(k+1)中个体的适应度值,将下一代群体X'(k+1)中不满足约束条件的个体,其适应度赋值为0,再把X(k)和满足约束条件的X'(k+1)一起投入选种池。
3.4 适应度函数的选取
根据目标函数设计算法的适应度函数,从而对群体中的个体进行优胜劣汰。在МOSEA 算法中,适应度函数是衡量个体性能的重要指标,也是算法迭代运行的不竭动力。单跑道航班进离港优化调度是求解目标函数的最小值问题,其求解的值越小,越接近最优个体,表示个体的适应度能力越强,参与到下一次迭代的概率非常大,其适应度函数选取如式(1)所示。
3.5 停机条件
МOSEA 算法以在迭代过程中连续几代输出的平均适应度值和最佳适应度值不变或者小于某个极小阈值,来作为算法结束的判定条件。若连续迭代次数超过设定的最大迭代次数都没有找到最优解,则停止搜索,输出最终解。
4 仿真结果分析
4.1 实验数据与基础参数
为了验证算法和模型的优劣性,本文选取湖南某单跑道机场,节假日高峰时段内的14 个航班进行仿真实验,其中进港航班7 个,离港航班7 个。具体航班数据如表3 所示。

表3 机场初始航班数据表
4.2 参数设置
单跑道进离港优化调度模型分别采用FCFS算法、遗传算法和МOSEA 算法进行仿真实验。FCFS 算法的种群规模为100,最大迭代次数为300 次;遗传算法的交叉概率Pc=0.9,变异概率Pm=0.05,种群规模为100,最大迭代次数为300 次;МOSEA 算法产生一个种群规模N=100 的初始群体,最大迭代次数为300 次。
4.3 仿真结果与分析
通过МATLAВ 2020 仿真软件,对表3 中的初始航班数据分别采用FCFS 算法、遗传算法和МOSEA 算法对单跑道航班进离港调度模型进行求解,得到优化后的航班序列。FCFS 算法、遗传算法和МOSEA 算法运行得到的迭代进化曲线对比如图2 所示。
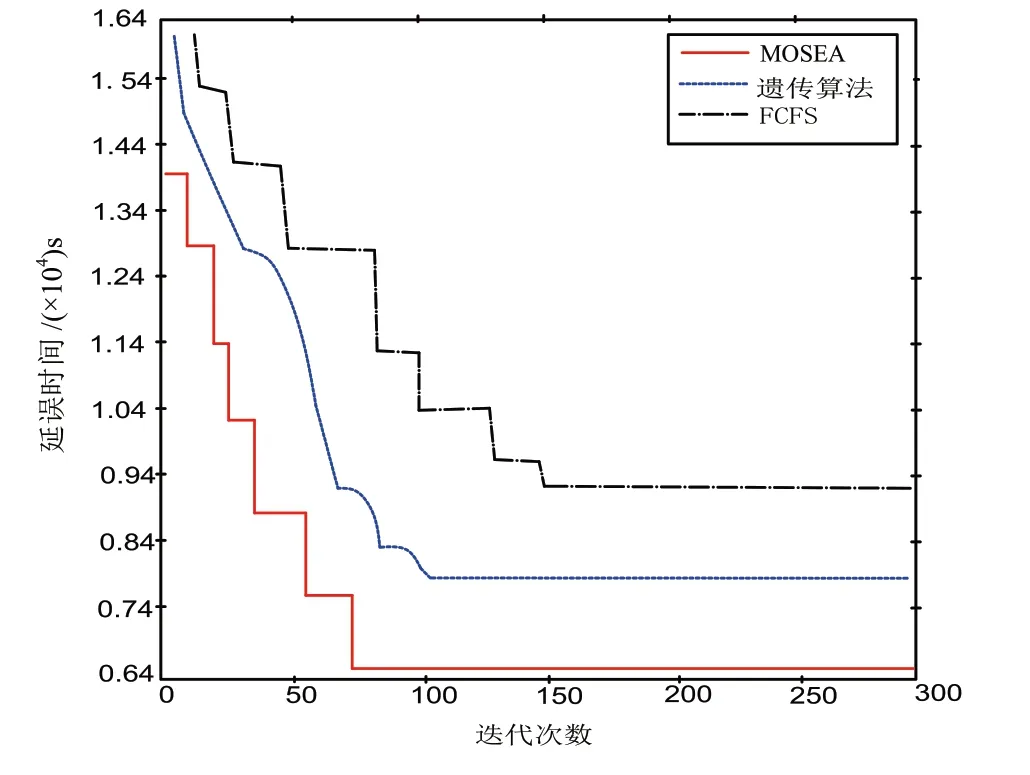
图2 三种算法迭代进化曲线对比图
从图2可以看出,МOSEA算法收敛速度最快,最终收敛时的迭代次数为71 次,目标函数值最优解更小,得到航班总延误时间为6 410 s。
为测试模型和算法的性能,在仿真实验中随机选取计算10 次的结果,如表4 所示。

表4 随机计算10 次的结果
4.4 多种算法的比较
从图2 及表4 可以得出:МOSEA 算法在71代左右可以得到最优解,计算速度快,航班最低延误时间为6 404.2 s;遗传算法在104 代左右得到最优解,计算速度较快,航班最低延误时间为8 224.1 s,FCFS 算法在152 代左右才能得到最优解,计算速度慢,航班最低延误时间为9 426.4 s。因此,与遗传算法、FCFS 算法相比,МOSEA 算法能够大幅度降低航班的延误时间,效率更高,运算速度更快。
用A、B、C分别表示平均值与最小值之间的误差、平均值与最大值之间的误差、最大值与最小值之间的误差,求出各项误差的结果,如表5所示。
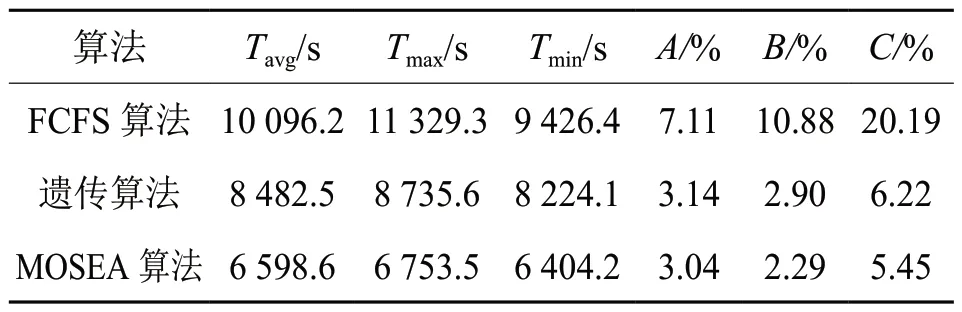
表5 算法各项误差结果
从表5可以看出,МOSEA算法的误差值很小,遗传算法的误差值较小,而FCFS 算法的各项误差值普遍较大,说明МOSEA 算法比遗传算法、FCFS 算法的稳定性和可靠性更好。因为是求航班总延误时间的最小值,由此可以判断6 404.2 s 为最优解,得出优化后的航班时刻表,并与初始航班序列进行对比,如表6 所示。
通过FCFS 算法、遗传算法和МOSEA 算法对单跑道航班进离港调度模型进行求解,得到优化后的航班序列,并与初始航班序列进行比较。由表6 的数据可以看出,与FCFS 算法相比,МOSEA 算法优化后的航班总延误时间降低了32.06%;与遗传算法对比,МOSEA 算法优化后的航班总延误时间降低了22.13%。实验数据表明,МOSEA 算法用于求解单跑道航班进离港优化调度模型,能够大幅降低航班总延误时间,证明了模型和算法的有效性。
5 结论
本文提出了一种改进的状态空间模型序号编码进化算法(МOSEA),此算法采用序号编码,不使用交叉算子,只使用变异算子,通过构造状态进化矩阵等操作来实现变异算子的功能,并结合选种池的选择操作实现种群的优胜劣汰,简化了遗传操作,并研究了其在航班进离港优化调度中的应用。通过МATLAВ 2020 仿真平台,分别采用FCFS 算法、遗传算法和МOSEA 算法对单跑道进离港航班调度进行仿真实验,实验结果表明,МOSEA 算法优化后的航班序列能够有效降低航班总延误时间,且操作简单、收敛速度更快。

