多RIS辅助的多用户上行MIMO系统信号检测算法

万 宇,景小荣,2,3

(1.重庆邮电大学 通信与信息工程学院,重庆 400065;2.移动通信技术重庆市重点实验室,重庆 400065;3.移动通信教育部工程研究中心,重庆 400065)

0 引 言

利用大量低成本无源反射器件设计的可重构智能表面(reconfigurable intelligent surfaces, RIS)[1],具有拓展无线通信覆盖范围、降低系统成本/功耗和提升通信性能的优势[1-2]。RIS作为极具应用前景的创新性技术,近年来广受业界关注。

目前,RIS技术研究主要集中于联合优化RIS单元反射系数及系统相关参数,以提升无线通信相关性能指标。针对多用户多输入多输出(multiple-input multiple-output,MIMO)系统,文献[3]通过联合优化RIS相移系数和发送功率分配,保证各用户的链路预算;文献[4]通过联合优化RIS相移系数和发射波束成形,最小化无线接入点(access point,AP)的发射功率;文献[5]通过联合优化有源和无源波束成形,实现用户加权和速率最大化。针对RIS辅助的毫米波(millimeter wave,mmWave)通信系统,文献[6]提出RIS无源波束成形和信息传输(passive beamforming and information transfer,PBIT)方案,通过对RIS反射元件进行索引调制,在增强主通信的同时,隐蔽地传输RIS私有数据。

上述研究工作中,通常假设系统配置单个RIS模块,希望借助RIS使得多用户系统获得更可靠的通信。然而,在实际多用户通信系统中,由于用户地理位置分布的随机性,当基站(base station,BS)与多用户间的直接链路被严重阻塞时,所形成的低秩BS-RIS信道将无法保证系统中多用户信号均能得到有效传输[7]。因此,在直接链路被严重阻塞的多用户系统中,为保证多用户信号可靠传输并减少信号盲点,可在系统中部署多个RIS模块。多RIS辅助的通信架构尽管有效地解决了多用户系统中信号盲点问题,但又同时面临众多挑战,BS端的信号检测就是其中亟须解决的首要关键问题。

对于多RIS辅助通信系统的信号检测问题,文献[8]针对多RIS辅助的点对点毫米波通信系统,基于多RIS辅助所形成的等价MIMO传输模型,根据期望一致性推理(expectation consistent inference,ECI),给出一种迭代信号检测算法。文献[9]针对多RIS辅助的多用户上行预编码MIMO系统,以最小化均方误差(mean-squared error,MSE)为准则,通过交替来联合优化设计RIS相移、预编码矩阵及线性/非线性接收组合矩阵,从而实现最小均方误差(minimal mean-squared error,MMSE)和非线性MMSE判决反馈均衡(MMSE-decision feedback equalization,MMSE-DFE)接收机设计。

在上述分析基础上,本文针对多RIS辅助的多用户上行MIMO系统,为实现有效的信号检测,以最大化系统和速率为准则,构建了一非凸优化问题。为了对该非凸问题进行求解,利用拉格朗日对偶变换[10]将原问题等价为其对偶问题,以交替优化方式来联合优化信号接收矩阵和RIS相移系数。在交替优化过程中,通过引入二次变换[11]技术来对多比率分式规划(fractional programming,FP)问题进行求解;对于RIS相移系数优化子问题,通过将其转化为二次约束的二次规划(quadratically constrained quadratic program,QCQP)问题,根据其单位模约束条件,采用半定松弛(semi-definite relaxation, SDR)算法实现求解[12],最后实现发送信号矢量恢复。数值仿真结果表明,本文算法可有效解决多RIS辅助MIMO通信系统中的信号检测问题,并且当RIS相移量化比特数为5时,可取得趋近于全精度RIS相移的性能。

1 系统模型

多RIS辅助的多用户上行MIMO系统如图1所示。图1中,上行链路包括一个配备Nd根接收天线的AP,K个用户和R个RIS。

假设第k个用户配备Nk根发送天线,其待传输信号向量用xk∈Nk×1表示,满足同时,假设R个RIS由一智能控制器集中调控其相位,其中第r个RIS由Mr个无源反射单元组成,其对角相移矩阵可表示为

Θr≜diag(φr,1,…,φr,mr,…,φr,Mr)

(1)

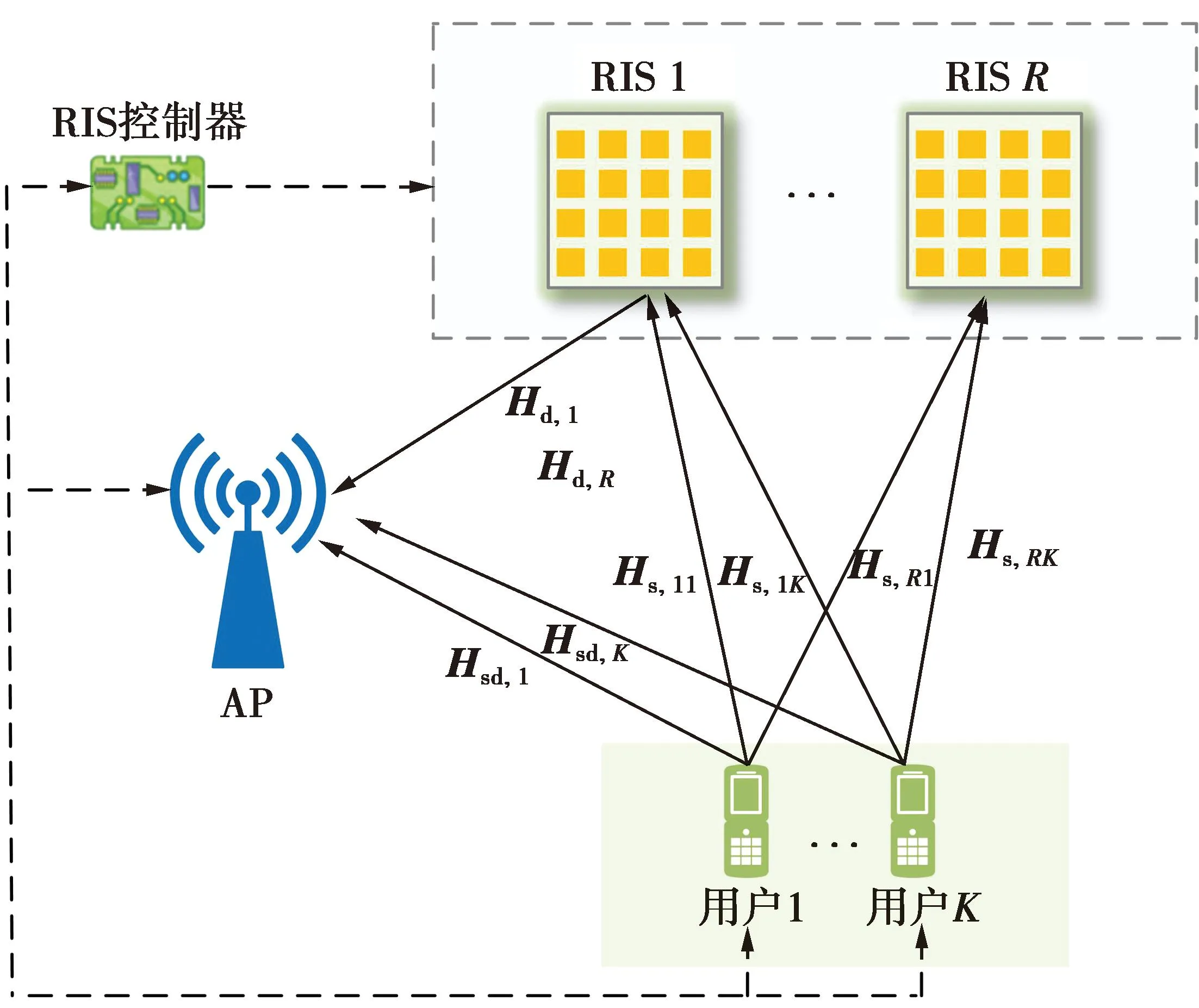
图1 多RIS辅助的多用户上行MIMO系统Fig.1 Multi-user uplink MIMO system assisted by multi-RIS

令Hsd,k∈Nd×Nk,Hs,rk∈Mr×Nk分别表示第k个用户到AP与第r个RIS的基带信道,Hd,r∈Nd×Mr表示第r个RIS到AP的基带信道,则AP处接收信号为

(2)

进一步,考虑准静态平坦衰落模型[9],信道在相干时间内保持不变。

2 问题描述

由(2)式,AP端接收信号为K个用户的叠加信号,对于用户k来说,除噪声外,剩下K-1个用户的信号均属于干扰信号,要实现有效的信号检测,需要同时考虑用户间干扰消除和背景噪声抑制。

(3)

因此,第k个用户的信干噪比(signal-to-interference-plus-noise ratio,SINR)为

(4)

对应地,系统可实现的和速率为

(5)

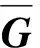
(6)

(7)

3 算法设计

优化问题P1的目标函数和约束均为非凸,很难通过直接解析求解获得最优解,本节基于FP给出一种次优解求解方法。

利用文献[10]中拉格朗日对偶变换,将优化问题P1等价为

(8)

s.t. (7)

(8)式中,α=[α1,α2,…,αK]T为引入的辅助变量。新的目标函数可改写为

(9)

(10)

s.t. (7)

将γk代入(10)式中的目标函数,于是优化问题P1″可改写为

(11)

s.t. (7)

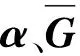
3.1 接收矩阵优化

固定Θ,问题P2简化为无约束优化问题,即

(12)

(13)

(13)式中,gk=vec(Gk),k=1,2,…,K。

由于P2′是一个多比率FP问题,因此,利用文献[11]中的二次变换技术,可将目标函数重新表述为

(14)

(14)式中,β=[β1,β2,…,βK]为辅助变量。

若A∈m×q,B∈q×n,Im为单位阵,则根据等价为

(15)

(16)

显然,P3是双凸优化问题,可通过交替更新β和g1,g2,…,gK来实现问题求解。

固定g1,g2,…,gK,可得

(17)

令∂f2(β,g1,g2,…,gK)/∂βk=0,得到辅助变量的解为

(18)

给定β,可得

(19)

令∂f2(β,g1,g2,…,gK)/∂gk=0,得到

(20)

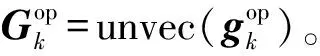
3.2 RIS相移Θ优化

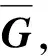
(21)

s.t. (7)

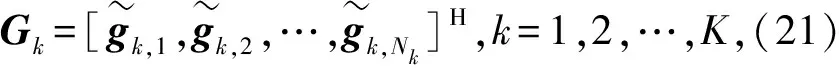
(22)

P4仍为一FP问题,可利用二次变换将其转化为

(23)

s.t. (7)

(23)式中,

(24)

(24)式中,η=[η1,1,η1,2,…,η1,N1,…,ηK,1,ηK,2,…,ηK,NK]为辅助变量。

类似地,可通过交替优化η和θ来实现求解。当固定θ时,令∂f3(η,θ)/∂ηk,n=0,得到

(25)

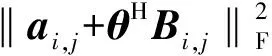
(26)

将(25)—(26)式代入(24)式中,去掉无关常数项,并将优化问题P4′中的约束等价为单位模约束:|φm|=1, ∀m=1,2,…,M,θ的优化问题可表示为

(27)

s.t. |φm|=1, ∀m=1,2,…,M

(28)

(27)式中

f4(θ)=θHQθ+2Re(θHp)

(29)

(30)

(31)

显然,P5是QCQP问题,通过引入辅助变量s把P5等效为齐次QCQP,即

(32)

(33)

(32)式中

(34)

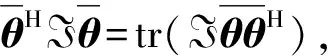
(35)

s.t.Φm,m=1,∀m=1,2,…,M+1

(36)

Φ0

(37)

优化问题P6为标准凸半定规划(semi-definite programming,SDP)问题,从而可利用CVX[14]求解器进行求解。但是,通常优化问题P6很难得到满足秩一的解,即rank(Φ)≠1,因此,需要采取额外步骤从优化问题P6的最优高秩解中构造秩一解[15]。具体地说,首先将Φ特征值分解为Φ=UΣUH,其中U∈(M+1)×(M+1)≜[u1,u2,…,uM+1]是一个酉矩阵,Σ=diag(λ1,λ2,…,λM+1)是对角矩阵,其中每一个元素对应Φ的每一个特征值。然后可以得到问题P6的次优解其中r∈(M+1)×1为服从(0,IM+1)的随机向量,利用T个独立生成的高斯随机向量r,容易找到使最大的最后再将转换为可行解即其中[e](1:M)表示包含e的前M个元素的向量。

3.3 文中所提信号检测算法步骤

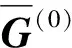
(38)

那么,xk的检测值为

(39)

算法1信号检测算法步骤

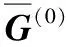
1: Fori=0:Imax-1

2:i=i+1

7: 利用SDR求解优化问题P6,获得Φ(i)

8: 先对Φ(i)进行特征值分解,再利用高斯随机化得到θ(i),则Θ(i)=diag((θ(i))H)

9: End for

3.4 所提信号检测算法复杂度分析

4 数值仿真与分析

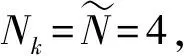
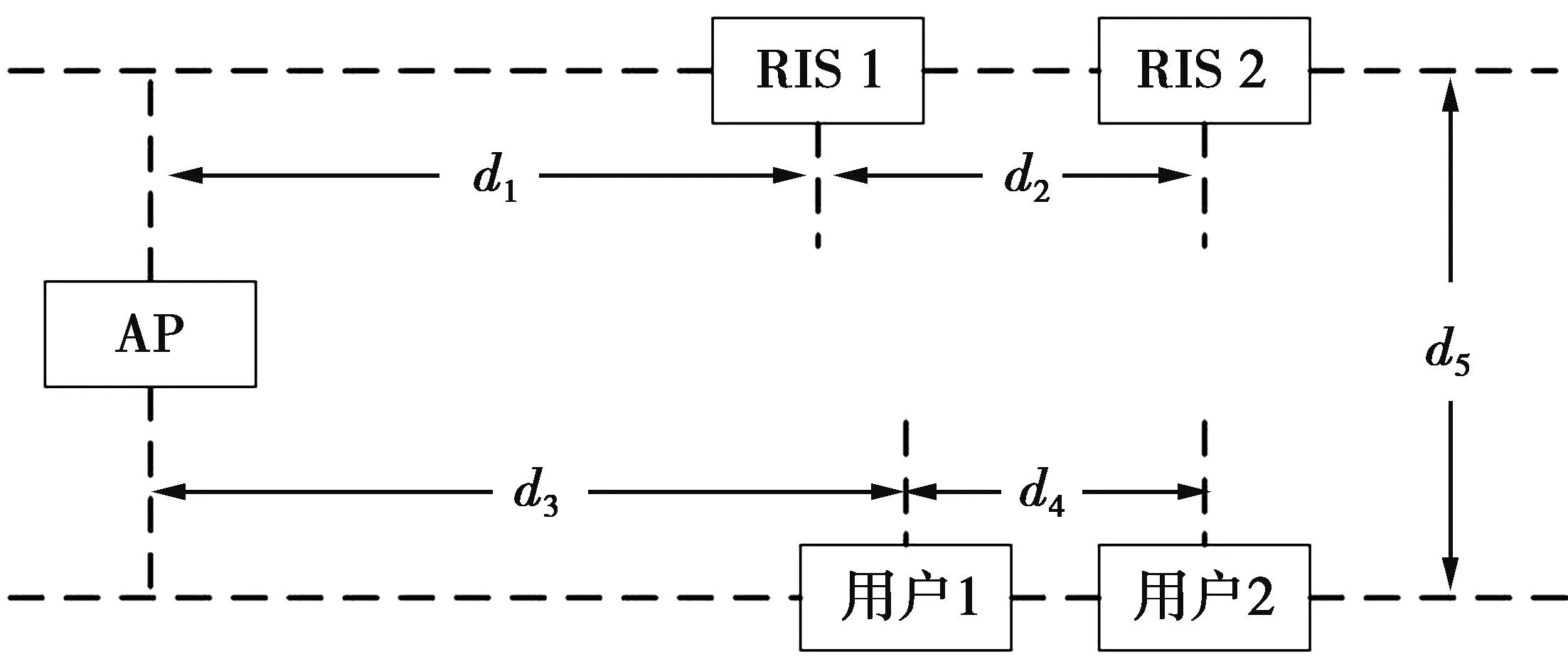
图2 数值仿真系统架构Fig.2 Architecture of numerical simulation system

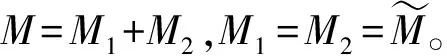
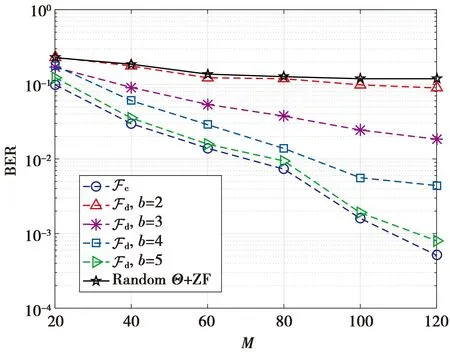
图3 BER随RIS总单元数M的变化曲线Fig.3 BER variation curves with the total number of RIS units M

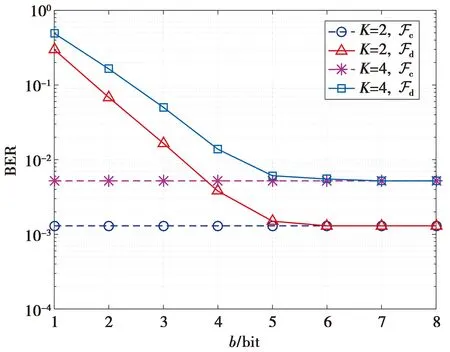
图4 BER随RIS离散比特数b的变化曲线Fig.4 BER variation curves with RIS discrete bit number b

图5给出本文算法随迭代次数变化的曲线。在图5中,利用不同b,K以及M的实例验证了算法的收敛性。考虑b=5的情况,当K=2,M=64时,系统BER在4次迭代后收敛到约10-2;当用户数从K=2增加到K=4时,系统BER仍在4次迭代后达到收敛,但性能稍有下降;当RIS总单元数从M=64增加到M=128时,K=2和K=4的收敛趋势均保持不变,且BER性能均明显提升。考虑b=4的情况,相较于b=5,系统BER性能有所下降,但算法收敛速度仍保持一致;对于其他RIS量化比特数也具有类似的结论。综上所述,本文算法能够实现快速收敛。

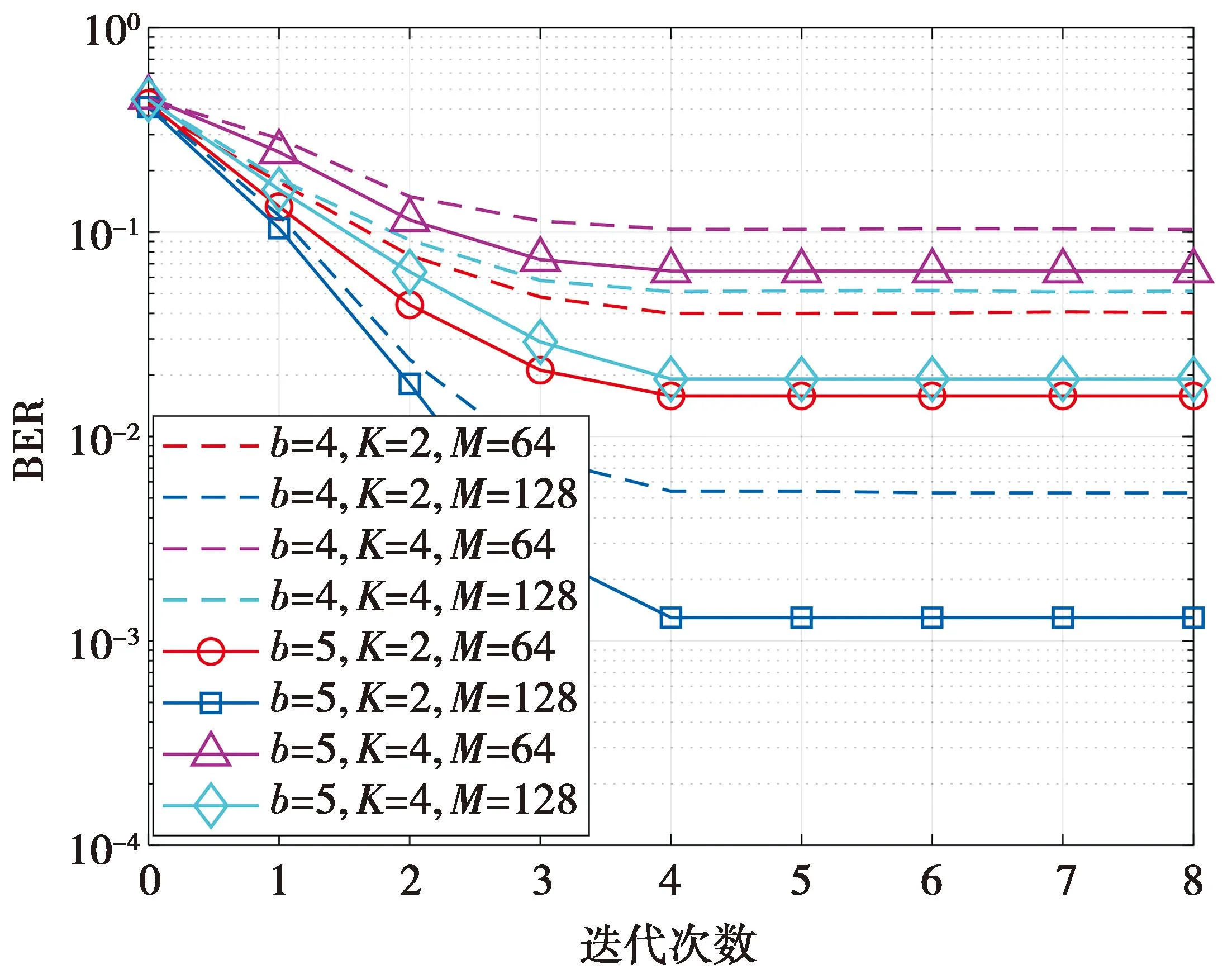
图5 BER随算法迭代次数的变化曲线Fig.5 BER variation curves with the number of iterations of the algorithm

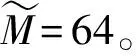
图6 BER随d3的变化曲线Fig.6 BER variation curves with d3

5 结束语

多RIS辅助通信可显著提高无线通信系统的性能,但同时会造成信号检测算法设计的复杂度增加。本文针对多RIS辅助的多用户上行MIMO系统中信号检测问题,以最大化系统和速率为目标,构建非凸约束的非凸优化问题,进而通过联合设计接收矩阵和RIS相移系数来消除多用户干扰和噪声的影响。仿真结果表明,在有限精度RIS相移条件下,本文所提的信号检测算法可显著提高系统的误码率性能,同时,当RIS相移量化比特数为5时,可取得接近于全精度RIS相移的性能。