恶意模型下汉明距离的保密计算
刘 新,涂小芬,胡翔瑜,徐 刚,陈秀波,刘晓梦
(1.内蒙古科技大学 信息工程学院,内蒙古 包头 014010;2.北京邮电大学 网络与交换技术全国重点实验室,北京 100876;3.北方工业大学 信息学院,北京 100144)
0 引 言
汉明距离[1]是指2个长度相等的序列X和Y之间同一位置元素不相等的数量,记为HMD(X,Y)。汉明距离在数据相似度计算、误差检测、数据清洗和文字查重等方面具有广泛应用[2]。如何在保护数据隐私的情况下,保密地计算字符串的汉明距离,成为亟待解决的问题。
安全多方计算由Yao[3]等提出,随后Goldreich[4]、Cramer[5]等对其提出了系统的论述。针对安全多方计算的研究包括保密数据挖掘[6-7]、保密的计算几何和集合问题[8]、保密的科学计算[9]等。这些研究推动了安全多方计算的发展,解决了许多实际问题[10-11]。
目前,汉明距离的安全计算协议并不多见,仅有的协议均是在半诚实模型下提出的。文献[12]中将汉明距离转换为集合相交问题,保密地计算2个集合的交集基数。文献[13]以此基础,利用高德瓦瑟-米卡列(GM)加密算法[14]在半诚实模型下设计了保密计算2个序列汉明距离的安全协议。但以上两协议的计算效率较低,本文在此基础上进行改进,利用椭圆曲线加密算法[15],设计了半诚实模型下保密计算汉明距离的安全协议,提升了协议计算效率,并用模拟范例证明了协议的安全性。
以上协议均在半诚实模型下完成计算,但参与者有可能是恶意的,所以半诚实模型下的协议有一定的局限性。因此,需要设计恶意模型下的安全多方计算协议来抵抗恶意敌手的攻击行为[16]。
本文定义了0-1编码规则,将字母字符串采用二进制编码方式进行编码后计算汉明距离,在分析了半诚实模型下保密计算汉明距离协议中可能存在的恶意行为基础上,利用零知识证明和分割-选择方法,设计了恶意模型下的安全计算协议,并利用理想-实际范例[16]证明了协议的安全性,同时分析了恶意敌手攻击成功的概率。
1 相关知识
根据安全多方计算中恶意模型的安全性定义,设计0-1编码规则,本文提出恶意模型下汉明距离的安全计算协议。因此,本部分对相关知识进行介绍。
1.1 汉明距离
在信息论中,汉明距离表示2个长度相等字符串中,同一位置上元素不相等的数量,例如“gyda”与“uyga”之间的汉明距离为2。在海量数据对比过程中,汉明距离可以反映数据之间的相似程度,以解决数据分类、数据筛选、数据重复等问题。在通信编码中,汉明距离可表达一个字符串转化为另一个字符串所需的转变次数,用于编码体系中的纠错、验错。在二进制中,a和b的汉明距离等于a⊕b结果中“1”的个数,例如“1010010”与“0110110”之间的汉明距离是3。
1.2 0-1编码规则
本文的2个协议中均需要将明文编码为二进制数,针对不同明文采用不同的二进制编码方式,能有效减少编码后明文的长度。对于少量固定几个字符序列的明文,往往采用一一对应的方式进行0-1编码,例如文献[13]中把脱氧核糖核酸(DNA)序列编码为二进制时,将A编为1000、C编为0100、G编为0010、T编为0001。对于具有26个英文字母字符串的二进制编码方式,往往采用将字母和空格一一对应转变为十进制,然后将十进制转变为二进制(5比特)的方式进行编码,编码如表1所示。
1.3 恶意模型的安全性定义
安全多方计算的参与者主要分为半诚实的和恶意的参与者[16]。半诚实参与者按照协议规则忠诚地执行协议,在执行过程中不会中途停止或提供虚假信息,但是他们可能会记录中间计算结果和最终结果,尝试推导其余参与者的信息。恶意参与者在执行协议过程中不遵守协议规则,可能篡改中间数据或终止协议等(不考虑提供虚假输入信息的情况,因为在理想模型协议中也无法避免这一情况)。恶意模型的安全性定义[16]如下。

表1 字母转化二进制列表Tab.1 Letter conversion binary list
恶意模型的安全性证明过程需要借助拥有可信第三方的理想协议来完成,由于理想协议是最安全的协议,如果设计的实际协议(恶意模型下)与理想协议具有相同的安全性,即可说明协议在恶意模型下是安全的。
1)理想协议。假设Alice和Bob拥有数据x和y,他们借助可信第三方(trusted third party,TTP)执行函数f(x,y)=(f1(x,y),f2(x,y))后,各自可得到结果f1(x,y)和f2(x,y),同时不会泄漏自己的数据x和y。如果Alice为恶意参与者,在收到数据f1(x,y)后终止协议,这种情况下TTP给Bob发送终止符号⊥,否则将f2(x,y)发送给Bob。

如果Alice是诚实的,那么
γ(x,y,z,r)=(f1(x,y′),B2(y,z,r,f2(x,y′)))
(1)
(1)式中,y′=B2(y,z,r)。
如果Bob是诚实的,那么
γ(x,y,z,r)=
(2)
在2种情况下x′=B1(x,z,r)。

定义1恶意模型的安全性。
(3)
那么,协议Π安全计算F,其中,x,y,z∈{0,1}*使得|x|=|y|并且|z|=poly(|x|)。
2 半诚实模型下汉明距离的保密计算
问题描述。假设Steven和Tom将自己的信息按照“0-1编码规则”都编码为一条长度为l的0-1字符串X=(a1,a2,…,al)和Y=(b1,b2,…,bl),Steven和Tom保密计算字符串X和Y的汉明距离HMD(X,Y)。具体协议如下。
协议1半诚实模型下保密计算汉明距离。
输入:Steven的字符串X=(a1,a2,…,al),Tom的字符串Y=(b1,b2,…,bl);
输出:HMD(X,Y)。
准备阶段。利用椭圆曲线加密算法,选择生成元为G,Steven选择私钥k,然后计算k·G=K得到公钥K,将公钥(K,G)发送给Tom。
步骤1Steven选择l个随机数ri,其中,i=1,2,…l,利用ri和K依次加密字符串X上的所有字符,得到长度为l加密向量Er(X)=(Er1(a1),…,Eri(ai),…,Erl(al)),加密过程如下
(4)
然后计算每个密文Er(ai)对应的标识符Ci=ri·G,最后将长度为l的加密向量Er(X)和l个标识符Ci发送给Tom,即(Er(X),Ci)。
步骤2Tom收到(Er(X),Ci)后,执行以下步骤。
步骤2.1:选择l个随机数si,其中,i=1,2,…l,利用随机数si和Steven的公钥K逐比特加密字符串Y上的每一个元素,得到长度为l的加密向量Es(Y)=(Es1(b1),Es2(b2),…,Esl(bl)),加密过程如下
(5)


T(Er(X)+Es(Y))=(Er(aT(1))+Es(bT(1)),
Er(aT(2))+Es(bT(2)),…,Er(aT(l))+Es(bT(l)))
(6)


步骤4Steven将计算结果Sum告知Tom。
协议1结束。
执行协议1过程中,参与者可能存在恶意行为,因此,需要对可能出现的恶意行为进行分析,并提出相应的解决方案。
3 恶意模型下汉明距离的保密计算
解决思路:基于半诚实模型协议1下可能存在的恶意行为,来设计抗恶意敌手的汉明距离保密计算协议2。但是,对于在理想协议中都无法阻止的恶意行为,恶意模型下的安全协议同样也无法阻止,因此也不予考虑,包括:①一方不参加协议;②任意一方输入虚假的数据;③一方突然终止执行协议。
分析协议1中可能出现以下恶意行为。
1)在协议1中,Steven拥有公私钥,而Tom只有公钥,不能解密,对于Tom来说不公平。解决思路是需要双方都具有公私钥,最终可以同时得到正确的计算结果,避免不公平性。
2)在Steven或Tom加密自己的数据时,执行过程中一方可能提供虚假的密文,从而导致结果错误。解决思路是利用分割-选择(cut-choose)方法来验证密文的正确性,但依然可能成功欺骗,但成功欺骗的概率随着引入随机数的增加而趋近于零。
3)Steven或Tom在协议1的步骤4中发送错误的数据给对方,使其无法计算出正确的结果。解决思路是在协议1中加入零知识证明,使得Steven和Tom可以验证数据的正确性。
3.1 具体协议
Steven和Tom各自选取公私钥,同时执行协议,但最后不用将结果HMD(X,Y)告知对方,而是各自将结果编码到椭圆曲线上,Steven得到点M1,Tom得到点M2。由于恶意模型下对方可能存在恶意行为,所以Steven和Tom需要对比M1和M2是否相等,若相等则计算结果正确,否则对方是恶意的。
协议2:恶意模型下保密计算汉明距离。
输入:Steven的字符串X=(a1,a2,…,al),Tom的字符串Y=(b1,b2,…,bl);
输出:HMD(X,Y)。
准备阶段。参与双方共同选择椭圆曲线加密算法生成元G,Steven和Tom分别选择自己的私钥k1和k2,并计算公钥K1=k1·G和K2=k2·G。Steven和Tom分别保密选择随机数s和t,并计算u=s·K1和v=t·K2,双方交换(K1,G,u)和(K2,G,v)。Steven和Tom各自执行到协议1的前3步后,将得到的结果编码为M1和M2,执行以下步骤。

(7)
(8)

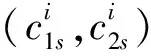

Steven计算公式为
a·(M2-M1)+a·t·G,P1=p1·G,λt=
p1·K2
(9)
Tom计算公式为
b·(M1-M2)+b·s·G,P2=
p2·G,λs=p2·K1
(10)
Steven和Tom将ct+P1和cs+P2发送给对方。
步骤5Steven计算ωs=k1·(cs+P2)发送给Tom,Tom计算ωt=k2·(ct+P1)发送给Steven。
步骤6Steven和Tom此时再将ct和cs发送给对方。
步骤7Steven计算ms=k1·cs发送给Tom,Tom计算mt=k2·ct发送给Steven。
步骤8Steven收到mt后利用零知识证明验证数据的真实性,即证明(mt=ωt-λt)是否成立。Tom收到ms后利用零知识证明验证数据的真实性,即证明(ms=ωs-λs)是否成立。若没有通过验证,则说明对方是恶意参与者。
步骤9若双方都通过验证,则Tom计算ms-b·u得到k1·b·(M1-M2),从而判断M1和M2是否相等,若相等则计算结果正确。Steven通过计算mt-a·v得到k2·a·(M2-M1),从而判断M1和M2是否相等,若相等则计算结果正确。
协议2结束。
3.2 正确性分析
1)Steven利用零知识证明验证Tom发送的mt,通过计算mt-a·v得到的结果是正确的,过程如下
mt-a·v=mt-a·t·K2=
k2·ct-a·t·k2·G=
k2·a(M2-M1)+k2·a·t·G-a·t·k2·G=
k2·a(M2-M1)
(11)
Tom利用零知识证明验证Steven发送的ms,通过计算ms-b·u得到的结果是正确的,过程如下
ms-b·u=ms-b·s·K1=
k1·cs-b·s·k1·G=
k1·b(M1-M2)+k1·b·s·G-b·s·k1·G=
k1·b(M1-M2)
(12)
2)在协议2的步骤8中零知识证明是正确的。由于Steven和Tom双方过程对称,所以只需要证明一方即可,这里假设Steven验证Tom发送的mt是正确的,即验证mt确实是用Tom的私钥k2与ct相乘得到的,分析如下。

3.3 安全性证明
需要分析协议2中Steven和Tom能否利用双方公布的数据,破解对方的输入数据或者提前得到输出结果。
2)在协议2的步骤6中,Steven和Tom发送加密数据ct和cs给对方后,因为Steven不知道cs=b·(M1-M2)+b·s·G中Tom选取的随机数b,所以无法计算出数据b·(M1-M2)来提前得到输出结果。同样,因为Tom不知道ct=a·(M2-M1)+a·t·G中Steven选取的随机数a,所以无法计算出数据a·(M2-M1)来提前得到输出结果。
3)在协议2中双方唯一可以达成欺骗的行为是在协议2的步骤1时提供虚假的密文,即在cut-choose时通过了验证,而对方在协议2的步骤4中刚好又选中了错误的加密数据,这样对方就无法得到正确的结论,但欺骗方也无法通过提供错误的密文来得到对方的输入,也无法提前得到输出结果。下面分析达成欺骗的概率(Steven与Tom的概率相同)。
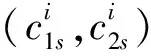
安全性证明采用理想-实际范例,即,对比模拟执行理想协议和实际协议2,若2个协议在计算上不可区分,即可证明协议2的安全性。
定理2恶意模型下的保密计算汉明距离协议2(记作Π)是安全的。

1)在理想模型中,B1模拟诚实的A1执行协议,给TTP发送正确的M1,且收到消息后一定会给发送消息B2。不诚实的B2调用A2来执行协议。B2把M2发送给A2,然后获取执行协议时A2使用的数据A2(M2)。B2向TTP发送A2(M2),然后获取数据F(M1,A2(M2)),同时B1也需要得到F(M1,A2(M2)))。

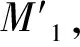
步骤2B2公布协议2的步骤2中A2要求A1公布的消息。



在理想模型中,B2严格执行协议Π并输出。B1接受输入M1并调用A1,获取A1实际执行Π时发送的消息A1(M1)。B1将A1(M1)发送给TTP后获取F(A1(M1),M2)。若实际协议中A1在第7步发送了解密的结果,并在第8步完了验证,则B1告知TTP发送结果F(A1(M1),M2)给B2;若实际协议中A1在第7步终止协议,或在第8步无法完成验证,则B1告知TTP给B2发送⊥。



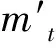

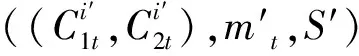
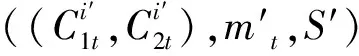

因此,协议2在恶意模型下是安全的。
4 性能分析
本文通过效率分析和实验仿真对协议性能进行分析,具体如下。
4.1 效率分析
1)协议1效率分析:协议1与文献[12]、[13]进行比较,假设0-1字符串长度均为l。文献[12]、[13]均采用GM加密算法,模数为N,文献[12]计算复杂度为4l次模指数运算,通信复杂度为1轮。文献[13]计算复杂度为3l次加解密运算和l次模N乘法运算,共需要7l次模指数运算,通信复杂度为1轮。本文的协议1中采用椭圆曲线加密算法,计算复杂度为15l次乘法运算,通信复杂度为1轮。
2)协议2效率分析:目前尚未发现恶意模型下汉明距离安全计算协议的提出。虽然文献[16]是针对百万富翁问题提出的恶意模型安全协议,与本文应用场景不同,但是其中的数据相等判断协议与本文协议2中比较两个汉明距离是否相等问题基本一致,因此,协议2与文献[16]进行比较。假设都加密m组密文。在计算复杂度上,文献[16]中采用Paillier加密算法,双方各自加密密文需要2m次模指数运算,验证时需要m/2次模指数运算,其余需要6次模指数运算,一个参与者需要2.5m+6次模指数运算,则整个协议计算复杂度为5m+12次模指数运算。本文协议2利用椭圆曲线加密算法,双方各自加密密文时只需要m次乘法运算,验证阶段不需要用到椭圆曲线上的乘法运算,其余只需要7次乘法运算,整个协议计算复杂度为30l+2m+14次乘法运算。在通信复杂度上,文献[16]通信复杂度为3轮,协议2需要4轮。
本文协议1和协议2与文献[12]、[13]和[16]进行对比,如表2所示。
在计算复杂度上,本文的协议1和协议2采用椭圆曲线加密算法,相比于GM加密算法和Paillier加密算法的模指数运算,椭圆曲线的乘法运算计算量较低。在通信复杂度上,协议2与文献[16]的通信轮数有所增加,但均能抵抗恶意敌手的攻击。协议2相比文献[16]仅增加了1轮交互,通信效率并无显著降低。

表2 方案对比Tab.2 Scheme comparison
4.2 实验仿真
为了验证协议的计算效率,本文利用Python语言进行模拟实验,采用配置为Intel Core i5-8400 CPU,8 GByte DDR4内存,512 GByte SSD硬盘的电脑运行实验。实验中椭圆曲线采用secp256k1曲线,恶意模型下m取20,l取10,模拟不同密钥长度下实验1 000次协议所用时间取平均值,如图1所示。

图1 效率对比Fig.1 Efficiency comparison
实验结果表明,本文采用椭圆曲线加密设计的协议1和协议2,在协议执行效率上较文献[12]、[13]和[16]有所提升。恶意模型下的文献[16]与半诚实模型下的协议1、文献[12]、[13]相比,恶意模型下的协议需要花费更多计算时间,但本文恶意模型下的协议2相比于半诚实模型下的文献[12]、[13],计算时间更短。从图1可以看出,随着密钥长度的增长,执行时间都有所增加,相比而言,协议1和协议2执行时间增加缓慢,且斜率相比而言增加较为平缓,是因为椭圆曲线加密数据仅使用乘法运算,而同级别下的GM、Paillier加密算法中使用的是模指数运算,因此,椭圆曲线加密算法具有耗时短、存储空间低等优点。
因为恶意模型下的安全多方计算协议需要使用cut-choose和零知识证明等方法,所以协议执行时间一般高于相同输入长度的半诚实模型下的协议,但可以采用云服务外包计算等方式来降低恶意模型下的计算开销。
5 结束语
保密计算汉明距离具有广泛的应用场景,现有安全多方计算协议大多是在半诚实模型下设计的,当有恶意敌手存在的情况下是不安全的。本文针对字母字符串进行0-1编码,利用椭圆曲线加密算法,首先设计了半诚实模型下保密计算汉明距离的协议,在此基础上分析恶意敌手可能的攻击行为,设计了恶意模型下保密计算汉明距离协议。恶意模型下的协议利用cut-choose和零知识证明方法,可以阻止或发现恶意行为,最后分析了协议的计算效率和通信效率,并进行了实验对比。本文构造的恶意模型协议更具有实用价值,为保密计算汉明距离提供了高效的解决方案。

