多天线无人机辅助通信系统资源优化方案研究
黄嘉琪,唐菁敏,王炳文,龙 华
(昆明理工大学 信息工程与自动化学院,昆明 650000 )
0 引 言
随着移动用户需求的逐渐增加,未来的无线网络服务有望提供无处不在的、可持续的高数据速率通信服务[1]。传统的无线通信系统主要由依靠固定的地面基站实现,然而复杂的通信环境将极大限制其发展[2-3]。无人机(unmanned aerial vehicle,UAV)辅助通信的高机动性和灵活性能有效解决这一问题[4],同时通过对UAV辅助通信系统轨迹规划和资源优化能进一步提升传输性能。
目前,众多专家学者对无人机轨迹规划和资源分配优化问题开展大量的研究。文献[5-6]提出了悬停飞行轨迹方案,通过优化无人机位置部署提高了系统性能,但是未充分利用无人机可移动性;文献[7]通过轨迹设计开发其机动性,提高无线通信系统的性能,若能在规划无人机飞行轨迹的同时优化资源分配,可以进一步提高吞吐量,从而带来更多的性能效益;文献[8]通过联合优化用户通信调度和无人机轨迹以及资源分配来最大化所有地面用户的最小吞吐量;文献[9-10]通过联合优化UAV飞行轨迹和发射功率分配,实现系统吞吐量的最大化。
然而,这些研究主要关注的是通信能耗的优化问题,并未考虑UAV的飞行能耗,而实际上UAV在飞行过程中需要的推动功率占比很大。虽然在文献[11]中考虑了UAV飞行能耗的问题,但是其仅考虑了单天线UAV的飞行能耗优化问题;随着毫米波、THz 等高频段通信技术的发展,天线尺寸减小,集成性强,对于负载能力较强的无人机,可装载多根天线,从而利用多天线技术提供更多的优势,文献[12]证实了多天线UAV可以进一步提高通信系统的吞吐量;文献[13]研究了波束成形和功率分配的联合设计,最大化数据传输速率。因此,多天线UAV在通信网络中能有效实现干扰抑制和提升能效。
综上所述,当前UAV辅助无线通信系统大多仅考虑通信能耗的影响,在资源分配研究中未能考虑飞行能耗。因此,本文在UAV总能耗受限的情况下,研究了系统的轨迹规划、飞行和通信功率分配等问题。
本文主要的研究工作如下。
1)建立了多天线UAV辅助地面用户通信的下行无线传输系统,规划UAV飞行圆轨迹,在飞行能耗和通信能耗、用户最低传输速率等约束条件下,设计一个联合优化UAV波束成形和飞行速度的资源分配方案来提高系统的总吞吐量。
2)通过块坐标下降法将非凸优化问题分解成2个子问题,引入松弛变量、一阶泰勒表达式、连续凸近似方法将2个非凸子问题转换成凸问题求解,然后对2个子问题交替迭代优化。
3)通过仿真对比实验,证明所提出波束成形和飞行速度联合优化方法,在满足用户通信质量的前提下,能有效提高系统的总吞吐量。
1 UAV基站通信系统模型
UAV基站通信系统如图1所示。
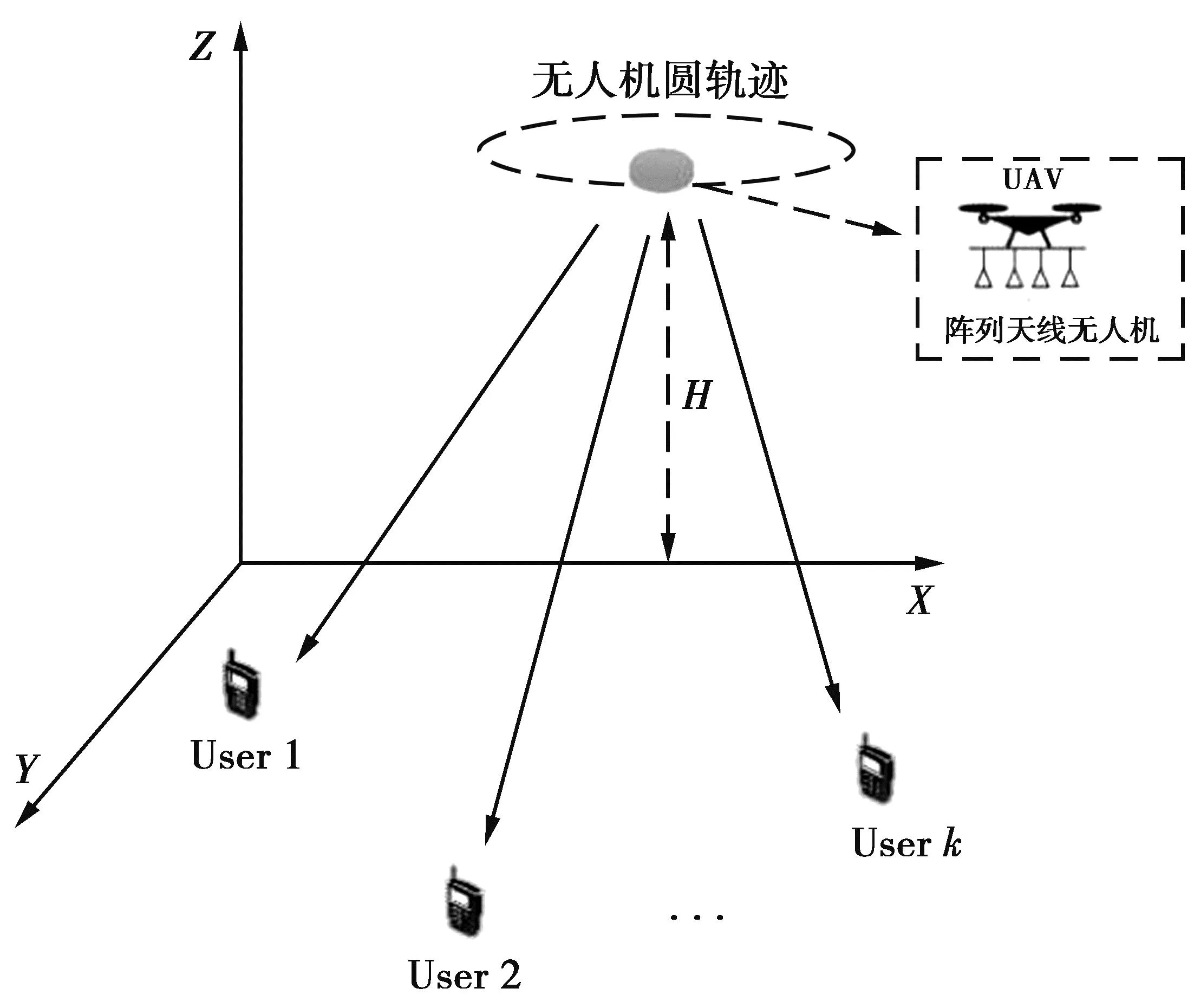
图1 UAV基站通信系统Fig.1 UAV base station communication system
图1中,考虑了一个多天线UAV辅助通信系统,该系统中包含1个含Nt根天线的UAV作为空中基站,假设工作的飞行高度为H,沿圆形轨迹飞行,飞行周期为T,为了方便研究,将T等分为N个时隙,每个时隙长度为δt=T/N,假设时隙δt足够小以保证无人机位置和速度在每个时隙内可以认为是固定不变的。此外,该系统有K个单天线地面用户,用户序号集合为k∈{1,…,K}。假设地面用户位置已知,第k个用户的坐标位置表示为gk=(xk,yk,0),定义UAV在第n个时隙坐标为q[n]=(x[n],y[n],H),n=1,2,…N,考虑到飞行能力限制,UAV的轨迹应满足的约束如下
‖q[n+1]-q[n]‖≤Vmaxδt,1≤n≤N-1
(1)
q[1]=qI
(2)
q[N]=qF
(3)
(1)—(3)式中:Vmax表示UAV的最大飞行速度;qI和qF分别表示UAV的初始位置和UAV的终止位置。
1.1 信道模型
假设UAV采用线性均匀天线阵列,则在第n个时隙,UAV与用户k的天线阵列响应为
ak[n]=[1,e-jπsin(θk[n]),…,e-j(Nt-1)πsin(θk[n])]
(4)
(4)式中:Nt为天线的个数;θk[n]为用户k与阵列法向量之间的夹角, 且为
(5)
由于UAV在一定高度与用户通信,未受障碍物的影响,因此,下行链路考虑视距信道模型。在第n个时隙UAV和用户k的信道增益可以表示为
(6)
(6)式中,β0为UAV与用户间距离1 m时的功率增益。
1.2 能耗模型
在整个飞行周期T内,UAV的总能耗Esum由通信能耗和飞行能耗组成,可表示为
Esum=Et+Ev
(7)
1)通信能耗。UAV提供通信传输数据消耗的能量,可表示为
(8)
(8)式中,wk[n]∈CNt×1表示在时隙n对用户k的波束成形矩阵,在每个时隙UAV均与所有用户通信,因此,每个时隙用户接收到的传输速率可以通过UAV分配的通信功率来调节。
2)飞行能耗。用来支持UAV飞行消耗的能量。根据文献[14],在第n个时隙UAV飞行消耗的功率为
(9)
(9)式中:c1和c2是常数,取决于UAV的重量、转子的速度、转子盘面积、叶片角速度和空气密度;Utip是转子的叶尖速度;d0是机身阻力比;vm是平均转子速度;ρ是空气密度;s是转子密度;A是转子盘面积;v[n]是UAV在第n个时隙的飞行速度。
因此,在整个飞行周期T内,UAV飞行消耗的能量可表示为
(10)
1.3 UAV飞行轨迹
为便于研究,规划了一种低复杂度的UAV圆轨迹飞行方案。
圆轨迹的圆心和半径均由用户的分布情况确定,分别用Cg=(Xcg,Ycg)和ru表示,圆轨迹规划尽可能地覆盖了所有用户,把用户分布的几何中心作为圆心位置,Cg可以表示为
(11)
(11)式中,gk′=(xk,yk)。
ru设置为Cg与所有用户之间的最大距离,表示为
(12)
则UAV第n个时隙飞行的弧度角近似于θ0[n],即为
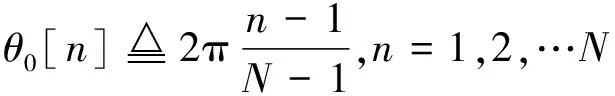
(13)
第n个时隙对应的位置坐标表示为
q[n]={Xcg+rucosθ0[n],Ycg+rusinθ0[n]},
n=1,2,…N
(14)
飞行速度为
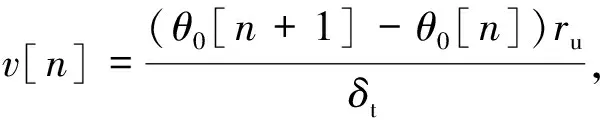
n=1,2,…N
(15)
2 吞吐量最大化问题的建立
用户k在第n个时隙接收到的信号为
(16)
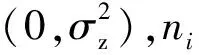
则在第n个时隙,用户k接收信号的干扰信噪比为
(17)
用户k的吞吐量可以表示为
(18)
在整个飞行周期T内,系统的总吞吐量可以表示为
(19)
为了提升整个系统数据传输吞吐量,考虑基于UAV多天线波束成形与飞行速度规划联合优化问题,该优化问题P1可以表示为
s.t. C1:Et+Ev≤pmaxT
n=1,2,…N
C4:q[1]=qI
C5:q[N]=qF
(20)
(20)式中:w={wk[n],∀k,n};q={q[n],∀n};v={v[n],∀n};C1表示UAV功率约束;pmax为UAV最大功率;C2表示UAV的轨迹约束;C3表示用户的最低的传输速度约束;C4和C5分别表示UAV的初始位置和UAV的终止位置。由于P1中目标函数和约束条件存在多变量耦合、非凸问题,难以直接求最优解,于是采用一种两层交替迭代算法来求解该问题的一个近似次优解。
3 UAV资源分配优化方案
为了解决P1这个非凸优化问题,利用块坐标下降方法分解2个子问题P2和P3,然后通过对2个子问题的交替迭代,直到目标函数值收敛[15]。
子问题P2是在固定UAV的飞行速度条件下,对多天线UAV波束成形矩阵优化。
子问题P3是在固定波束成形矩阵条件下,对UAV的飞行速度优化。
3.1 波束成形优化
固定飞行速度变量v,问题P1转变为关于变量w的子问题P2,即
s.t. C1:Et≤pmaxT-Ev
(21)
该子问题P2是非凸的,因为目标函数和约束条件C2中的Rk[n]都是关于wk[n]非凸的,为解决这一问题,通过利用连续凸近似(successive convex approximation,SCA)技术[16]来处理。首先通过一阶泰勒展开式推导Rk[n]的一个近似上界,然后对该近似上界进行迭代计算逼近原来的非凸约束。
目标函数中的Rk[n]可以写为
(22)
(22)式中:
(23)
由于R2i[n]是凹函数, 凹函数在任意点的一阶泰勒展开都是其全局上界[16]。因此,R2i[n]在第u次迭代时的全局上界为
(24)
s.t. C1:Et≤pmaxT-Ev
(25)
子问题P2.1是一个凸优化问题,可以直接利用凸优化工具CVX求解。
3.2 UAV飞行速度优化
基于P2子问题获得的解,作为子问题P3的初值。关于优化变量v的子问题P3表述为
s.t. C1:Ev≤pmaxT-Et
n=1,2,…N
C4:q[1]=qI
C5:q[N]=qF
(26)
目标函数和约束条件C1和C3都是非凸的,为了求解该问题,目标函数和约束条件C3利用连续凸近似方法来处理。对于约束条件C1,通过引入松弛变量,利用一个近似下界代替约束条件C1,通过迭代计算逼近原来的约束条件。
目标函数和约束条件C3中Rk[n]都是关于q[n]非凸的,Rk[n]展开如下
(27)
(27)式中,ak[n]是关于q[n]的复杂函数,导致子问题P3很难直接求解,于是利用上一轮迭代出来的ql-1[n]近似q[n]。
Rk[n]关于变量q[n]是非凸的,但是目标函数相对‖q[n]-gk‖2是凸函数,凸函数在任意点的一阶泰勒展开都是其全局下界。Rk[n]在第m次迭代时的全局下界为
(28)
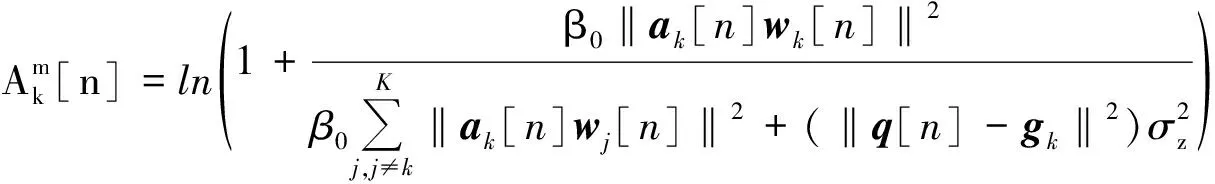
(29)
(30)
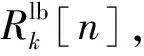
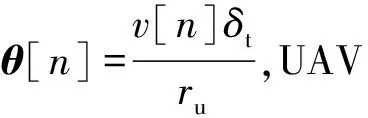
q*[n]={Xcg+rucosθ[n],Ycg+rusinθ[n]}
n=1,2,…N
(31)
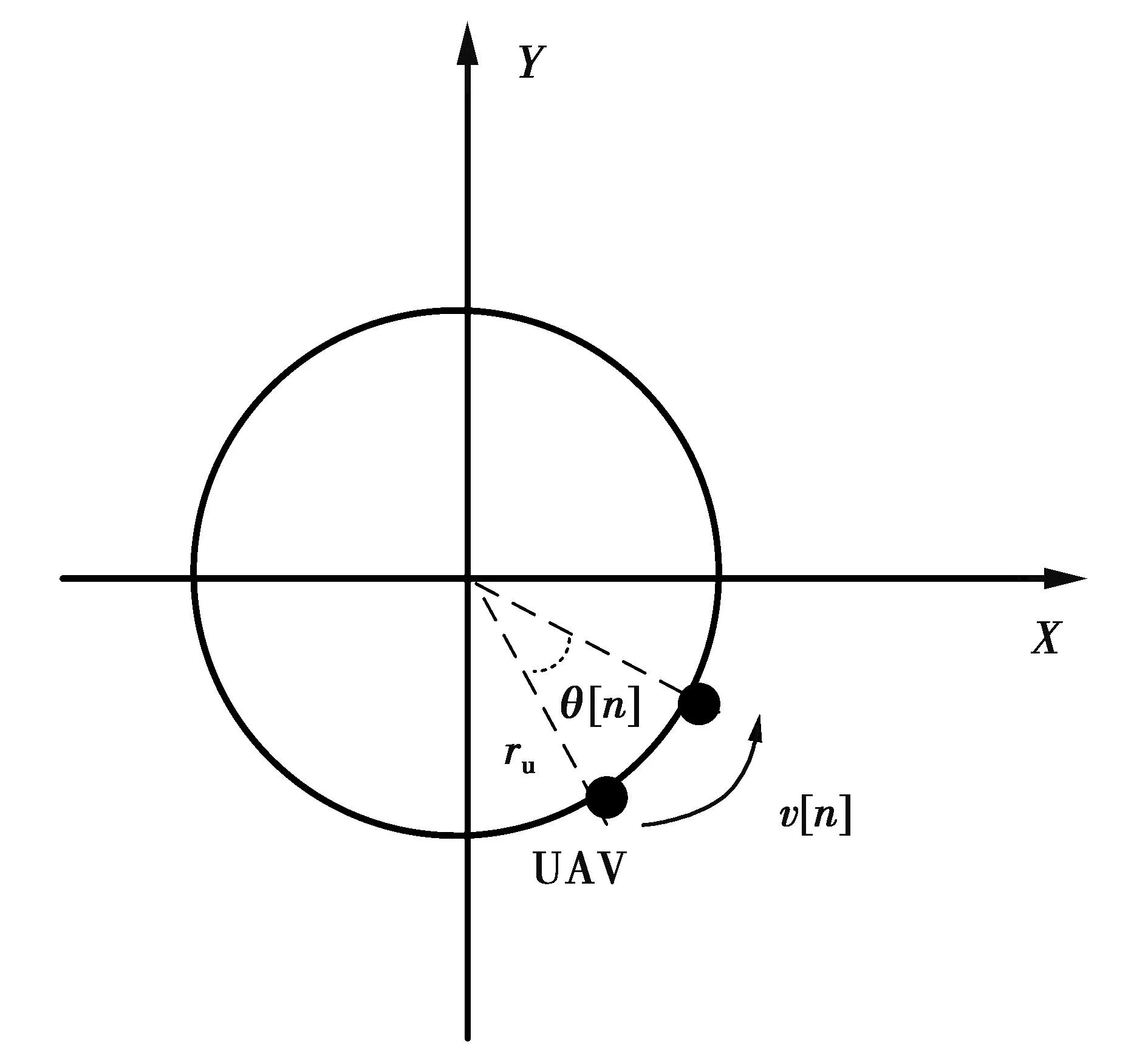
图2 第n个时隙UVA的轨迹坐标与速度的关系Fig.2 Relationship between trajectory coordinates and velocity of the nth slot UVA
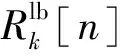
由于约束C1是非凸的,引入一个松弛变量φn≥‖v[n]‖,于是,C1中的p(v[n])可以改写为
(32)
(33)
UAV的飞行能耗近似于一个凸函数,表示为
(34)
综合上述分析,子问题P3可以转换成子问题P3.1。
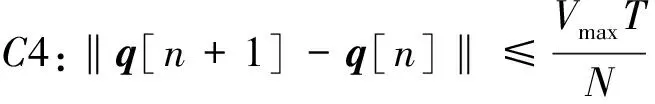
n=1,2,…N
C6:q[1]=qI
C7:q[N]=qF
(35)
问题P3.1是一个凸优化问题,可以使用凸优化工具CVX求解。由于问题P3.1的约束条件C1-C3隐含了问题P3的约束条件C1,通过求解过程P3.1得到的解保证是问题P3的可行解,因此,问题P3.1目标值的获得,通过解决问题P3.1在第m+1次迭代的解,且必须不小于在第m次迭代中获得相应的目标值,由于问题P3.1的目标值上方有界,因此,解决问题P3.1的迭代被保证收敛。
3.3 算法设计与分析
综上所述,基于块坐标下降法(block coordinate descent method,BCD)的资源分配方案如算法1所示。
算法1基于BCD的资源分配算法
初始化系统参数:w(0),q(0),v(0);设置最大迭代次数Lmax;迭代次数l=0;
步骤1:Repeat;
步骤2:l=l+1;
步骤3:根据给定的q(l-1),v(l-1),通过(25)式更新w(l);
步骤4:根据给定的w(l),q(l-1),通过(35)式更新v(l),并且根据(31)式得到q(l);
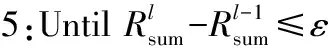
步骤6:结束并输出结果。

4 仿真分析
为了验证本文提出方案的有效性和优越性,考虑了一个配备8根均匀天线阵列的UAV基站为随机分布在500 m×500 m的6个单天线用户提供通信服务。用户的位置通过随机产生得到,分别为g1=[360, 111],g2=[26, 403],g3=[128, 194],g4=[187, 38],g5=[171, 338],g6=[307, 429]。选取qI=[210, 25],qF=[190, 25],H=100 m,T=100 s,N=50,δt=2 s,v0=15 m/s ,Vmax=50 m/s,pmax=30 dBm,α=0.3 bit/s/Hz,ε=10-2;接收信号的噪声功率σz=-100 dBm,相对参考距离的信道增益β0=-60 dB。仿真过程中其他参数如表1所示[18]。

表1 仿真参数Tab.1 Simulation parameters
图3展示了根据用户分布位置规划的UAV飞行圆轨迹。UAV运动轨迹尽可能覆盖所有用户,在保证所有用户通信质量前提下也尽可能兼顾了用户通信服务的公平性。

图3 UAV飞行圆轨迹Fig.3 UAV flight circle trajectory
图4给出了不同波束成形方案下系统吞吐量与时间的关系。随机波束成形方案采用的是随机生成相应的波束成形矩阵。由图4可见,当T=80 s时,优化波束成形的吞吐量是22.37 bit/s/Hz,而随机波束成形的吞吐量是16.89 bit/s/Hz;优化波束成形的方案所获得的系统吞吐量明显优于随机波束成形方案的,且随着时间T的增加,两者的差距越来越大。因此,对比随机波束成形,本文提出的波束成形方案使得系统总吞吐量得到了较好提升。
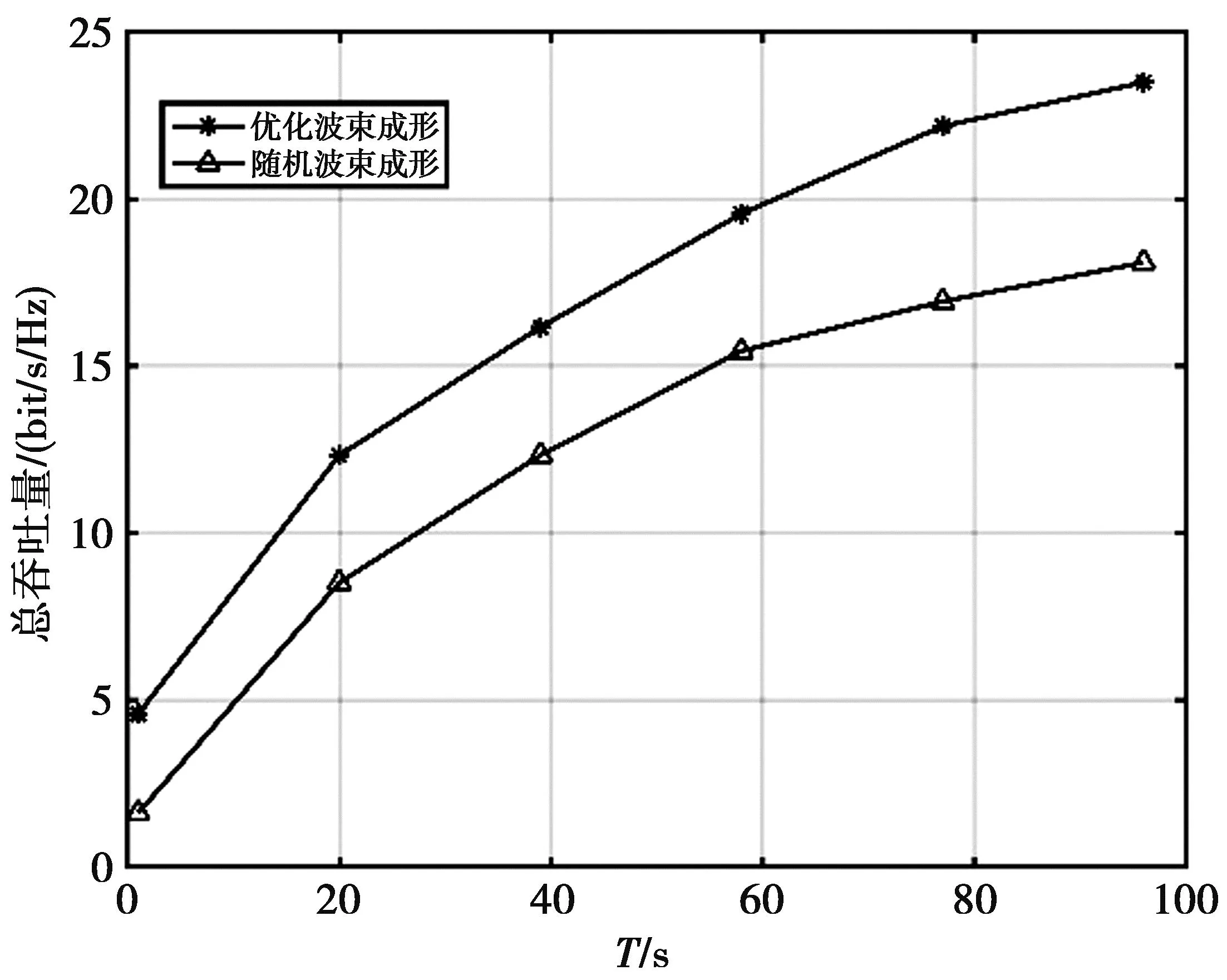
图4 不同波束成形方案下的系统总吞吐量Fig.4 Total system throughput under different beamforming schemes
图5给出了2种飞行速度方案下UAV最大功率限制与系统总吞吐量的关系。当pmax=30 dB时,UAV优化速度飞行的吞吐量是19.15 bit/s/Hz,而UAV匀速飞行的吞吐量是16.88 bit/s/Hz。随着最大功率限制pmax的增加,吞吐量也持续增长。由图5可知,速度优化飞行方案获得的总吞吐量明显高于匀速飞行方案的,并且随着功率限制的增加,差距持续增大。这是由于优化UAV飞行速度可以节约飞行能耗,补偿通信能耗,从而提升了系统的总吞吐量。
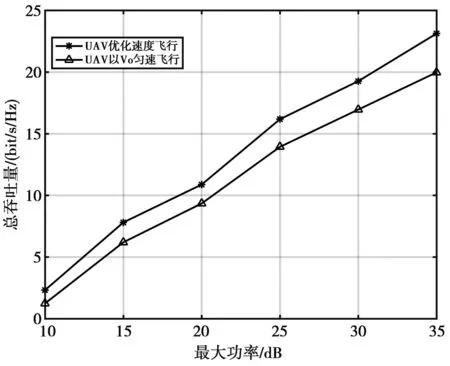
图5 优化速度和匀速两种飞行方案下的总吞吐量Fig.5 Total throughput under two flight schemes of optimized speed and uniform speed
图6给出了本文波束成形和UAV飞行速度联合优化方案,与单一优化波束成形(UAV匀速飞行)、单一优化UAV飞行速度(随机波束成形)作对比。由图6可知,所提算法比单一优化波束成形和单一优化UAV飞行速度分别提高了8.13 bit/s/Hz、6.32 bit/s/Hz;随着迭代次数增加,总吞吐量都随之升高并最终收敛,并且所提出的算法在迭代次数为24次后收敛到唯一值,说明提出的资源分配算法具有良好的收敛性。
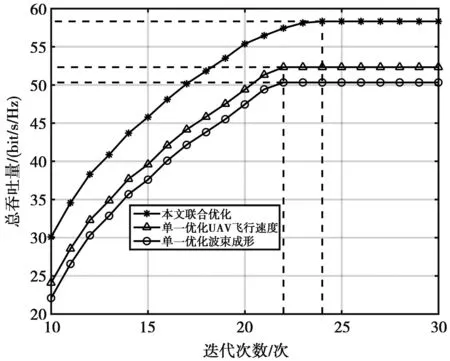
图6 迭代次数与总吞吐量的关系Fig.6 Relationship between iteration times and total throughput
5 结束语
本文研究了UAV辅助无线通信系统下的资源分配问题,提出一种基于BCD的资源分配算法。首先考虑了UAV总能耗、移动轨迹和用户最低传输速率等约束,然后建立了多变量耦合的系统最大化总吞吐量问题,通过块坐标下降法将优化问题分解成2个子问题,对2个子问题交替迭代优化,最后得出原优化问题的近似次优解。仿真结果表明,所提算法能有效提高系统总吞吐量,并且无人机飞行速度优化方案比无人机匀速飞行的方案性能更好。下一步主要工作是将无人机的飞行轨迹优化以及用户的移动性作为重点研究内容。

