基于改进麻雀算法的集装箱装卸设备调度优化

王 旭 董春芳

（东北林业大学机电工程学院，黑龙江 哈尔滨 150000）

港站作业区是集装箱海铁联运的重要组成部分，当2 个区域距离较远时，需要借助自动导引运输车（AGV）完成集装箱在两者之间的往返运输。船到达港口靠岸后，船上集装箱通过岸桥吊装到AGV 上，然后由AGV 运至堆场中，由轨道门吊进行吊装摆放。但目前一些作业区的装卸设备配置不合理、设备调度不科学等，导致集装箱装卸作业效率低下。因此根据港口作业模式对装卸设备合理配置和作业调度优化、提高装卸作业效率、缩短船舶在港时间以及提高整体运输网络服务水平具有重要作用。

目前许多学者对这类问题进行了研究。Liu[1]等提出了一种适用于直接转运和间接转运2 种模式的双目标整数规划模型，应用NSGA II 进行求解，验证模型有效性。Lu[2]等研究了一个新的约束模型。以优化起重机的综合调度问题和卡车行驶路径，旨在最小化装卸作业的最大完工时间。

该文针对装载作业过程中集装箱的存储位置和各类装卸设备的调度问题，研究“岸桥-AGV-轨道门吊”3 种设备的协同作业调度，在考虑设备数量约束的前提下，以岸桥完成卸载任务的时间最短为目标建立模型，以期更精准地提升港站作业效率，避免设备浪费。

1 模型建立

1.1 模型假设和符号说明

针对港口作业区装卸设备协同调度和配置方案，该文提出如下假设：1）所建立模型中的集装箱型号一致。2）各装卸设备能够连续完成装卸作业，并且作业过程中无故障。3）已知装卸任务在船舶和堆场的位置信息和AGV 的初始位置[3]。4）轨道门吊堆放集装箱时遵循先下后上的原则。

1.2 模型建立

1.2.1 目标函数

建立以最小化作业完工时间和设备配置数量最少为目标的混合整数规划模型，如公式（1）所示。

式中：a为作业完工时间的权重系数；b为设备配置数量的权重系数；为装卸作业结束时间（nk为设备，i为装卸集装箱），k∈{1，2，3}；N为所有装卸设备集合。

1.2.2 约束条件

有且只有一个装卸设备对每个装卸任务进行作业的表达，如公式（2）所示。

岸桥、轨道门吊和AGV 最多有一个前续集装箱作业的表达如公式（3）所示。

岸桥、轨道门吊和AGV 最多有一个后续集装箱作业的表达如公式（4）所示。

当岸桥连续作业2 个装卸任务时，后一个装卸任务的开始时间应晚于前一个装卸任务的结束时间和该设备在两装卸任务之间的空驶时间之和，如公式（5）所示。

卸车过程中岸桥等待AGV 的时间如公式（6）所示。

装车作业过程中岸桥等待AGV 的时间如公式（7）所示。

卸载作业中，岸桥的开始作业时间应晚于AGV 完成前一作业后并返回岸桥处的时间，如公式（8）所示。

式中：αi为集装箱需要进行的作业类别，当集装箱i∈Ku时，αi=1。

装车过程中，岸桥的作业开始时间应晚于AGV 的到达时间，如公式（9）所示。

岸桥作业的开始时间与结束时间的关系如公式（10）所示。

当AGV 连续作业2 个集装箱时，后一个装卸任务的开始时间应晚于前一个装卸任务的结束时间和设备在2 个作业之间的空驶时间之和[4]，如公式（11）所示。

卸车过程中AGV 等待轨道门吊的时间如公式（12）所示。

在卸载作业中，AGV 的作业开始时间应晚于岸桥的作业结束时间，如公式（13）所示。

轨道门吊的运行速度对AGV 作业结束时间的影响如公式（14）所示。

当轨道门吊连续作业2 个集装箱时，后一个装卸作业的开始时间应晚于前一个装卸作业的结束时间和设备在2 个作业之间的空驶时间之和，如公式（15）所示。

卸车过程中轨道门吊等待AGV 的时间如公式（16）所示。

在卸载作业中，轨道门吊的开始时间应晚于AGV 完成前一作业后并返回岸桥处的时间，如公式（17）所示。

轨道门吊作业开始时间与作业结束时间的关系如公式（18）所示。

2 改进麻雀搜索算法

2.1 算法设计思想

与其他优化算法相比，麻雀搜索算法（SSA 算法）控制参数较少，局部搜索能力较强，可用于车间调度[5]、路径规划[6]等问题的优化。但传统的SSA 算法在搜索初期易陷入局部最优点，因此一些学者对该算法进行了改进。刘丽娜[7]等利用量子计算、正余弦搜索和警戒者数量递减策略对SSA 进行改进，避免算法在求解后期陷入局部最优。王海瑞[8]等引入Tent 混沌提高初始解质量，同时优化了麻雀位置更新公式，以提高SSA 的工程实用性。该文在种群初始化阶段引入Levy 飞行搜索机制以增大搜索空间，提高群体搜索多样性，最大限度地提高装卸作业效率。

2.2 传统麻雀搜索算法

在麻雀觅食的过程中，根据麻雀的任务不同，将其分为发现者和加入者。发现者通过搜寻发现食物位置，加入者则依赖于发现者获取食物。此外，当麻雀种群受到捕食者的攻击时会做出反捕食行为。

首先，发现者通过搜寻发现食物，同时为加入者提供寻找方向，因此发现者能够获得比加入者更大的觅食搜索范围，如公式（19）所示。

式中：t为当前迭代次数；Xij为第i个麻雀种群在第j 维中的位置信息；α为的0～1 的随机数；itermax为最大迭代次数；Q为一个服从正态分布的随机数；L为一个1×d 并且元素全为1 的矩阵；R2属于0～1，表示麻雀种群位置的预警值；ST属于0.5～1，表示麻雀种群位置的安全值。

当R2ST时，表示种群中部分警戒者已发现天敌，全体种群应先转移至安全区，再进行食物搜寻。

其次，在搜寻食物的过程中，一些加入者会紧跟发现者。当发现者寻觅到食物后，加入者会同发现者进行争夺或者围绕在发现者周围进行觅食，如公式（20）所示。

式中：Xpt+1为目前发现者所发现的最佳位置；Xworst为当前全局最差的位置；A+=AT（AAT）-1，A为一个与麻雀个体同维度的列向量，其元素随机赋值为1 或-1 的1×d的矩阵。

当i≤n/2 时，加入者会积极追随发现者的觅食路径；当i>n/2 时，表明第i个加入者没有搜寻到食物，因此需要飞往其他地方进行觅食。

最后，在种群中，有一部分麻雀在搜寻食物的同时还肩负侦察敌人的任务，由于处在种群外围的麻雀很容易受到天敌的攻击，因此它们需要不断调整位置，该文称其为警戒者，如公式（21）所示。

式中：Xbest为当前全局最优位置；β为一个属于-1～1 的随机数，fi为当前麻雀个体的适应度值；fg为全局最佳适应度值；fw为全局最差适应度值；ε为一个避免分母为0 的常数。

当fi>fg时，表示麻雀在种群外围，极易受到天敌攻击；当fi=fg时，表示处于种群中间的麻雀也感受到天敌的危险，此时需要靠近其他麻雀以减少被攻击的风险。

2.3 改进麻雀搜索算法

针对传统麻雀搜索算法的缺点，该文在种群初始化阶段引入Levy 飞行搜索机制以增大搜索空间，提高群体搜索多样性，避免搜索算法陷入局部最优。另外，麻雀搜索算法需要仔细的参数调优才能获得最佳性能，因此增加Levy 飞行组件可以提供额外的探索机制并提高算法的鲁棒性，以减少对参数调优的依赖。

Levy 飞行扰动步长Tp的计算如公式（22）～公式（24）所示。

式中：i∈{1，2，…，n}；j∈{1，2，…，D}；u和v属于正态分布；β=1.5。

麻雀搜索位置步长扰动如公式（25）所示。

3 算例分析

随着海铁联运的快速发展，港口的货物吞吐量日益增多，为满足日益多样化的运输市场对高质量运输的需求，港站作业区需要对装卸设备进行合理配置、优化装卸设备调度，以适应更高的运输压力。该文以某港装卸作业设备协同调度为例进行分析。

该港某码头共有4 台岸桥供装卸船，在集装箱堆场设置3 台轨道门吊进行作业，往返港口与堆场的运输AGV 数量为9 辆。装卸设备的基本参数信息见表1。

运行结果见表2。针对该问题，与遗传算法（GA）相比，改进后的麻雀搜索算法所得设备配置更合理且目标函数值更优。

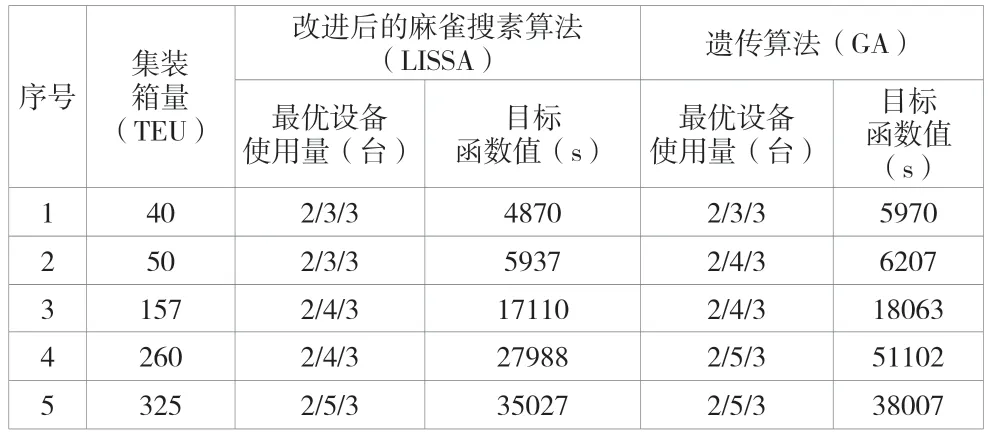
表2 LISSA 与GA 运行结果对比

根据算例分析可得：1）改进后的麻雀搜索算法性能较稳定，能够较快计算出目标函数最优解。不同参数设置下的性能比较如图1 所示。在箱量较小的情况下，该算法能较快达到收敛。2）目标函数值随集装箱吞吐量增加而增大，并且岸桥及轨道门吊的数量变化比AGV 的数量变化对目标函数的影响更大。3）以集装箱量40TEU 为分析对象，箱量规模较小，将其存储至一个箱区，根据模型求得的最优设备使用量为2/3/3，即有2 台岸桥投入使用，每辆岸桥到达集卡所需时间为97s。岸桥将靠岸船舶装载的集装箱卸下并装至AGV 上。在码头与堆场之间有3 辆AGV 正在行驶，AGV 将集装箱由港口运至堆场，然后轨道门吊将集装箱放置到指定位置。装卸作业完成时间和3 种设备的作业时间见表3，3种设备的详细使用方案见表4。

图1 不同箱量设置下的算法性能比较

表3 装卸作业完成时间（单位：s）

表4 设备详细使用方案

4 结论

该文主要研究了港口作业区装卸设备配置，在“岸桥-AGV-轨道门吊”的港口协同装卸方案下，首先分析了3种设备之间的时间衔接。其次建立以装卸任务完成时间最少和设备使用数量最少为目标的设备调度模型。最后，将某港码头运箱量代入模型进行求解。通过算法对比，发现改进后的麻雀搜索算法性能更稳定，可求解出较适当的设备使用数量和最短的作业完工时间，能够在一定程度上提升整个堆场的作业效率。由于该文没有考虑船舶的泊位利用率和港口装卸线数量对作业效率的影响，因此今后的研究中有待改进，以丰富海铁联运集装箱转运的研究内容。