基于K-means 算法和积灰损耗系数的中国西北地区光伏电站清洗策略建模分析

宗 嵩，曾维才，陈志勇,2，赵多元,2，何建军，黄财源

(1.国家电投五凌电力有限公司宁夏事业部，银川 750011；2.平罗县阿特斯佳阳新能源有限公司，石嘴山 753400；3.长沙理工大学，长沙 410114)

0 引言

随着实现碳达峰、碳中和政策的提出和落实，太阳能、风能等新能源在中国的应用越来越广泛。中国西北地区大部分区域的年太阳辐照量大于1700 kWh/m2，是建造光伏电站的绝佳地区[1]。但这些区域大多属于荒漠地区，风沙大，相对于建在黄粘土地带沙漠地区的光伏电站，建在此类地区的光伏电站其光伏组件表面更容易积灰[2]。长期积累在光伏组件表面的灰尘等杂质从透光率、温度、腐蚀等多方面影响着光伏组件的发电量，严重时输出功率损耗最高会达到30%[3-6]。文献[7]通过对甘肃省某光伏电站在不同季节光伏组件表面积灰速率和积灰对透光率的影响进行试验，发现春季时光伏组件表面每天平均积灰密度为5.309 g/m2，透光率平均每天减少1.49%。文献[8]在兰州市开展实验，发现当积灰密度达到2.068 g/m2时，光伏组件输出电流约下降22.6%，平均每天下降1.51%。文献[9]在呼和浩特市城区开展了倾斜玻璃和光伏组件表面的积灰量与光伏组件日平均总透射衰减率的实验，发现当积灰量分别为2.75、4.59、5.86 g/m2时，光伏组件日平均透射总透射衰减率分别为1.29%、3.42%、4.71%。因此，为了降低积灰对光伏电站发电量的损耗，开展清洗作业十分必要。

然而，在缺水和劳动力昂贵的中国西北地区，光伏电站频繁清洗会造成巨大的经济损失，而清洗间隔时间过长光伏组件表面积灰严重，也会导致巨大的能量损失。因此，需要在清洗成本和光伏电站运行损耗费用之间找到平衡，根据光伏电站的各方面条件制定合理的清洗策略[10-11]。光伏电站现阶段常用的清洗时间计算方法可总结为[12]：对比发电量损失率、计算输出功率损失率、周期性策略。但上述方法存在诸多弊端，对比发电量损失率是指对比清洗前后的光伏阵列的发电量，但这种方法忽略了发电量损失必然存在的客观事实；计算输出功率损失率时需要配备专业的设备和操作人员测试光伏电站中某个光伏阵列的I-V曲线，前两种策略都容易造成清洗后光伏电站收益不升反降的情况；周期性策略则因为不能确定积灰导致的发电量损失与清洗成本之间的关系，应用时的准确性受到限制。

本文在周期性策略的基础上，针对其缺陷引入光伏组件表面积灰损耗系数来反映积灰对光伏组件发电量下降的影响程度，采用K-means算法[13]聚类发电日志数据得到晴天数据样本来拟合求解积灰损耗系数值，结合光伏电站运行损耗费用和清洗费用建立经济周期函数模型；并以中国西北地区某光伏电站具体运行数据为例，对模型进行算例分析。

1 清洗策略建模过程

本清洗策略模型建立过程为：计算光伏电站的理论发电量，利用K-means 算法聚类光伏电站的发电日志数据得到计算清洗周期的晴天数据样本，并以此拟合得到积灰损耗系数，建立经济周期函数模型确定最佳清洗周期和清洗经济阈值，具体建模流程如图1 所示。

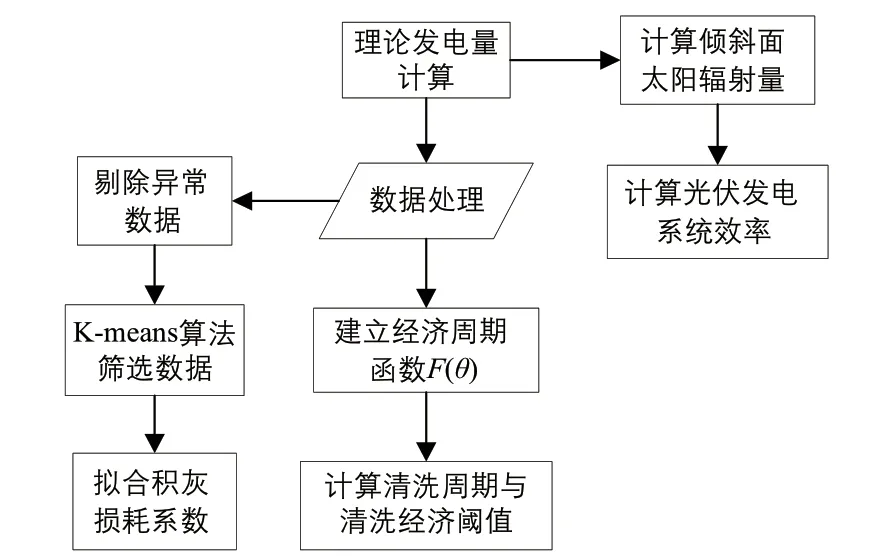
图1 建模流程图Fig.1 Flow chart of modeling

1.1 计算过程

1.1.1 倾斜面上太阳总辐射量

对于以某一倾角固定式安装的光伏阵列，光伏组件倾斜面所接到的太阳总辐射量与光伏阵列倾角、太阳高度角有关，计算示意图如图2 所示，图中：S为水平面上太阳直接辐射量，kWh/m2；β为光伏阵列倾角，(°) ；α为正午时分的太阳高度角，(°)。

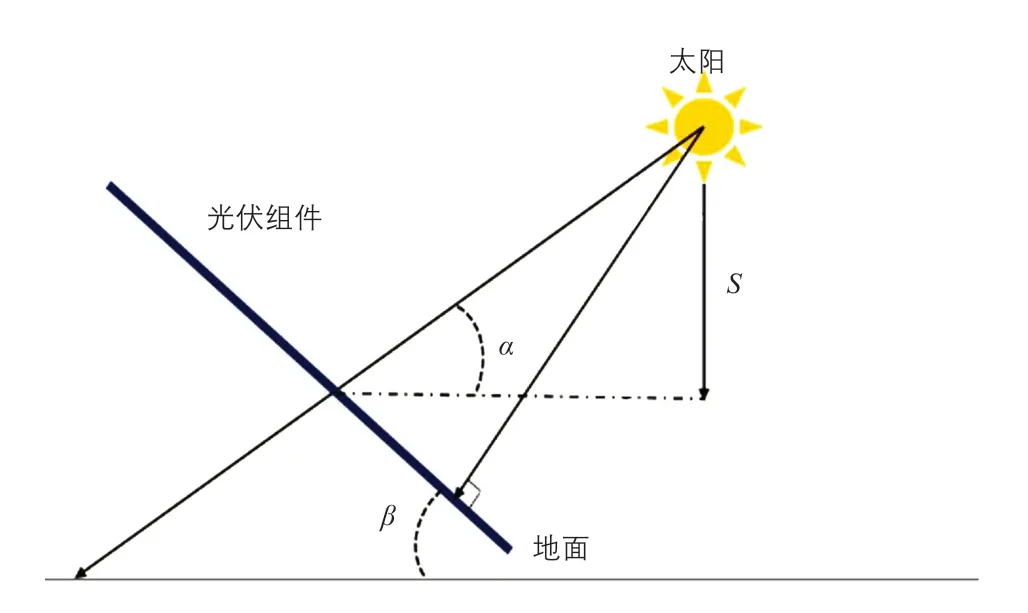
图2 倾斜面上太阳总辐射量的计算示意图Fig.2 Calculation diagram of total solar radiation on inclined square array

计算式[14-15]如式(1)所示。

式中：Rβ为光伏组件倾斜面上的太阳总辐射量，kWh/m2；D为太阳散射辐射量，kWh/m2。

其中，正午时分太阳高度角的计算式为：

式中：a为光伏电站所在地的纬度，(°)；b为太阳直射点纬度，(°)。

1.1.2 光伏发电系统效率

光伏发电系统由若干光伏阵列、并网逆变器、变压器，以及交流、直流线缆组成[16-17]最终并网，其示意图如图3 所示。

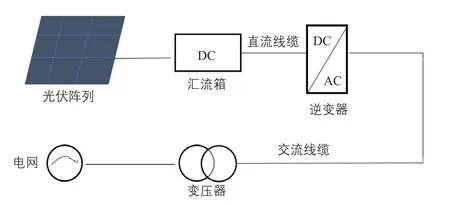
图3 光伏发电系统构成示意图Fig.3 Composition diagram of PV power generation system

从光伏组件直流端到电网交流端，导致发电量损失的因素包括光伏组件功率衰减、交直流线路损失、逆变器和变压器损耗等，将这些损耗等效为光伏电站系统效率K1，其表达式为：

式中：η1为光伏阵列发电效率，光伏阵列在能量转换过程中的损失包括光伏组件功率衰减、温升损失、直流线路损失等；η2为逆变器转换效率，等于逆变器交流输出功率与直流输入功率之比；η3为并网效率。

1.1.3 理论发电量计算

除上述计算的光伏组件倾斜面上的太阳总辐射量和光伏电站系统效率，还需考虑光伏组件的光电转换效率K2，得到理论发电量WL计算式[18]为：

式中：Spv为光伏组件总面积，m2。

1.2 K-means 算法

为了从光伏电站提供的发电日志数据中筛选聚类出天气为晴天且各方面环境参数指标相近的一类天气数据样本，模拟无极端天气如大风、降雨等气候时光伏组件表面的自然积灰过程，采用K-means 算法对样本数据进行聚类。

1.2.1 算法原理

K-means 算法是基于典型的、根据距离划分类别的无监督聚类算法。对于给定的样本集，按照样本间的距离大小将样本划分为K个簇。本文采用欧氏距离d作为样本中心与被凝聚点之间的距离，其计算式为[19-20]：

式中：x、y为同一维度下样本的不同属性；n为样本个数。

1.2.2 算法步骤

K-means 聚类过程可以概括为4 点，具体步骤如图4 所示。

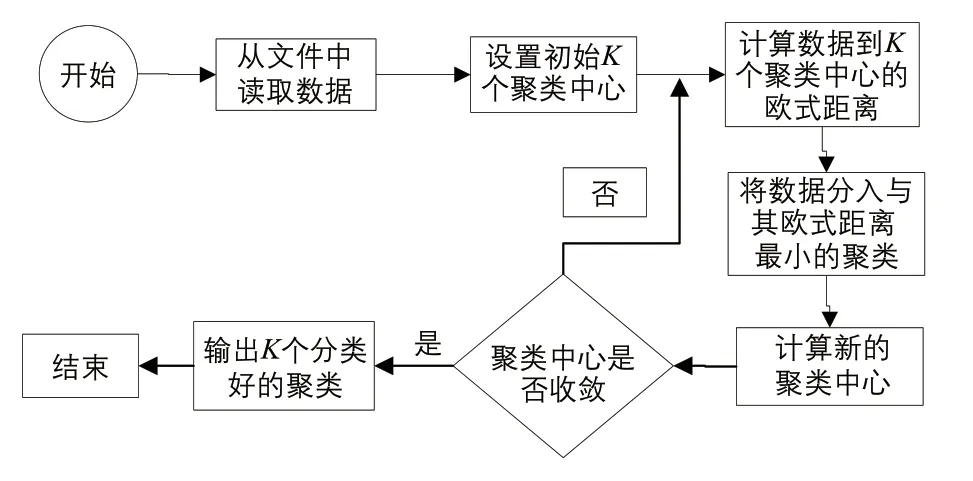
图4 K-means 聚类过程图Fig.4 Flow chart of K-means algorithm

1)首先确定K值，即数据经过聚类得到的集合数。从给定的数据集中选择K个数据点作为质心。

2)计算除质心外的剩余数据与每一个质心的欧式距离，根据最近距离准则将剩余数据归类到对应质心所属集合。

3)前两步将所有的数据归类得到K个集合，然后重新计算每个集合的质心。如果新计算的质心和原来的质心之间的距离小于设置的阈值，则表示重新计算的质心的位置变化不大，数据整体趋于收敛。此时可认为达到了期望的聚类效果，算法可终止。

4)如果新质心与原质心距离变化很大，则需重复迭代第2)、3)步直至达到收敛状态。

1.3 光伏组件表面积灰损耗系数

联立光伏组件理论发电量与实际日发电量的计算式，定义光伏组件的实际发电能力Lp，利用K-means 算法筛选聚类的晴天数据样本拟合发电能力与积灰时间θ0的数学曲线。积灰损耗系数γ的数值等于曲线的斜率。光伏组件发电能力的计算式可表示为：

式中：Wr为实际日发电量，kWh。

1.4 清洗策略模型

在经过K-means 算法聚类后得到的晴天数据样本范围内，拟合的灰尘动态积累造成的光伏电站发电量损失费Lθ与清洗周期总有效时长θ的数学曲线可近似考虑为线性增长模型，如图5 所示。

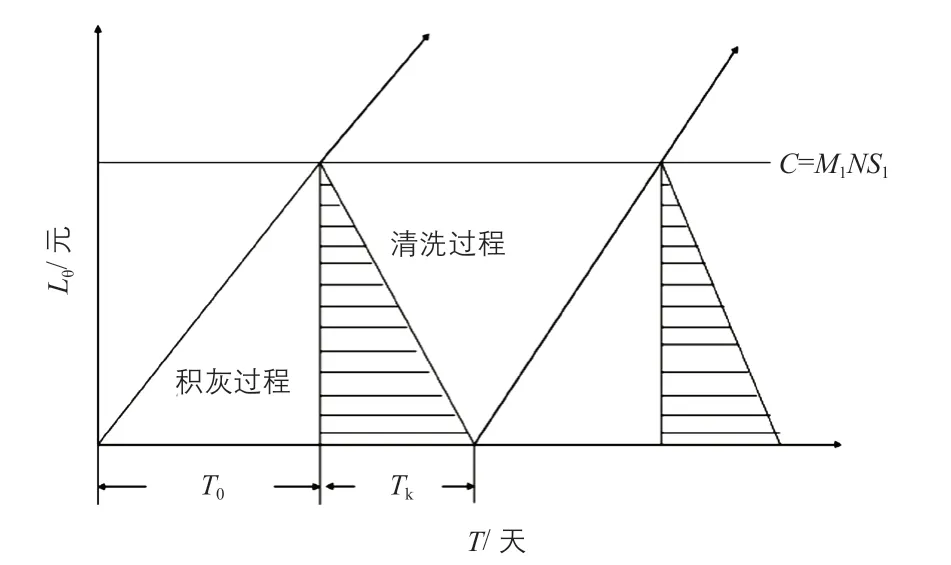
图5 光伏电站发电量损失费与最佳清洗周期的关系Fig.5 Relationship between power loss cost and best cleaning cycle

图中：C为光伏电站清洗成本；Tk为清洗时间；TD为动态积灰持续时间。结合光伏电站的清洁成本建立经济周期函数，即：

式中：M0为光伏发电单位度电成本，元/kWh；WL,i为第i个样本的理论发电量，kWh；Hi为第i个样本的有效发电时间，h；γ为积灰损耗系数；M1为单位面积光伏组件清洗成本，元/m2；N为清洗的光伏组件个数；S1为单块光伏组件面积，m2。

由图5 可以看出：最佳清洗周期T由两部分组成，清洗时间与清洗设备、场站地形等因素有关视为固定值，因此最佳清洗周期仅由动态积灰持续时间所决定。利用平均有效时长来消减多云或阴雨天气的不确定性影响，最佳清洗周期可表示：

其中，动态积灰持续时间可表示为：

式中：n'为某一阶段内光伏组件的实际运行天数。

从图5 还可以发现，当光伏电站发电量损失费与清洗成本相等时经济周期函数取得最佳值，对应的动态积灰持续时间即为临界积灰持续时间，结合式(7)～式(11)得到动态积灰持续时间的最终计算式为：

为了预警积灰造成的光伏组件发电量的损失，引入清洗经济阈值M，当发电量的损失费超过阈值时，参考未来几天的降雨等气候情况确定是否开展清洗作业。清洗经济阈值的计算式可表示为：

式中：C0为每千瓦时清洗成本，元/kWh；M2为上网电价，元/kWh；η4为光伏组件清洗经济系数。

综上，可得到光伏电站最佳清洗周期公式：

2 算例分析

为验证本清洗策略模型对于中国西北地区光伏电站的适用性，以该地区某光伏电站提供的2020 年12 月的发电日志数据为例进行验证分析。

2.1 数据处理

采用K-means 聚类算法对12 月的31 个发电日志样本数据进行处理，得到的晴天数据样本如表1 所示，数据的处理过程如下：

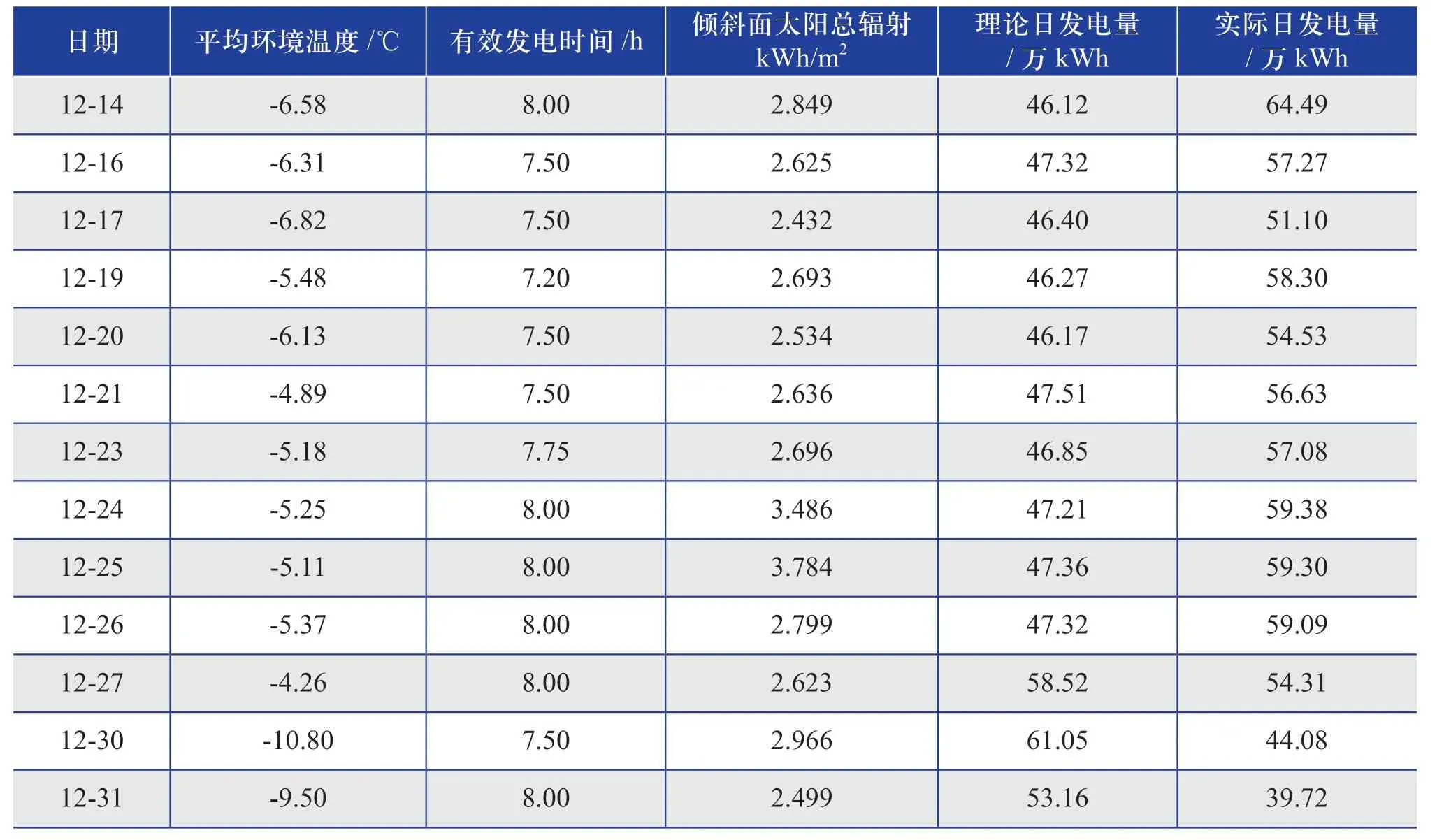
表1 筛选聚类得晴天样本数据Table 1 Sunny samples data obtained by screening and clustering

1)剔除包含故障光伏组件的光伏阵列数据及限电时段数据等异常数据。

2)选取12 月中晴天、晴转多云、多云、多云转阴4 个有代表性的天气下的样本数据各自成为聚类中心，每个聚类中心是一列向量。

3)计算剩余样本数据与4 个聚类中心之间的欧式距离。根据最近距离准则，将余下的27 个样本数据逐个归入4 个凝聚点作为初始分类，并计算各类的质心(均值向量)作为新的凝聚点。

4)重复第2)、3)步骤得到调整后的4 类样本数据，如果此步骤之后的31 个样本数据的分类结果与上一步的归类一致则停止运算，否则重复步骤第3)、4)。

2.2 积灰损耗系数拟合

根据表1 中的数据，利用软件拟合积灰导致的实际发电能力与积灰持续时间之间的一元线性回归方程，如图6 所示，其相关参数如表2 所示。由此可得积灰损耗系数为0.0286。

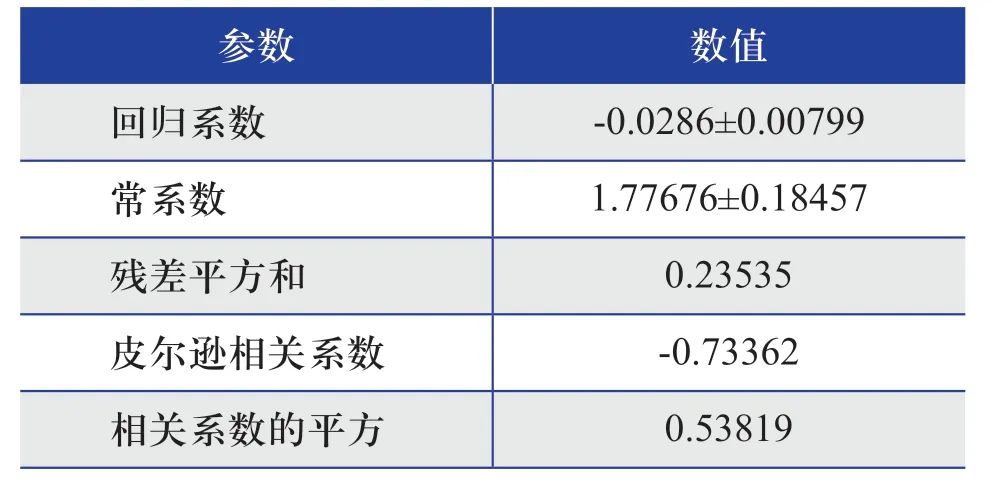
表2 光伏组件实际发电能力与积灰持续时间方程的相关参数Table 2 Equation parameters of actual power generation capacity and ash deposition duration of PV modules

图6 晴天时光伏组件实际发电能力与积灰持续时间拟合曲线Fig.6 Fitting curve between actual power generation capacity of PV modules and duration of dust deposition in sunny days

2.3 数据结果计算

以计算得到的清洗周期及清洗经济阈值来衡量模型的准确性。调研光伏电站得到光伏组件数、当地上网电价、单块光伏组件清洗成本及清洗时间，结合表1 的数据计算，并将计算结果与积灰损耗系数代入式(12)得到最佳清洗周期为60 天。

将清洗经济系数，单位千瓦清洗成本代入式(13)计算清洗经济阈值为18.33%～21.30%。结合光伏电站长期的运行经验，模型的计算结果准确性较高，适用于该地区的光伏电站。

2.4 清洗预警分析

结合清洗经济阈值对光伏电站2020 年的发电数据进行预警分析，发现3 月和12 月的发电数据经计算分析达到清洗阈值，数据曲线如图7所示。

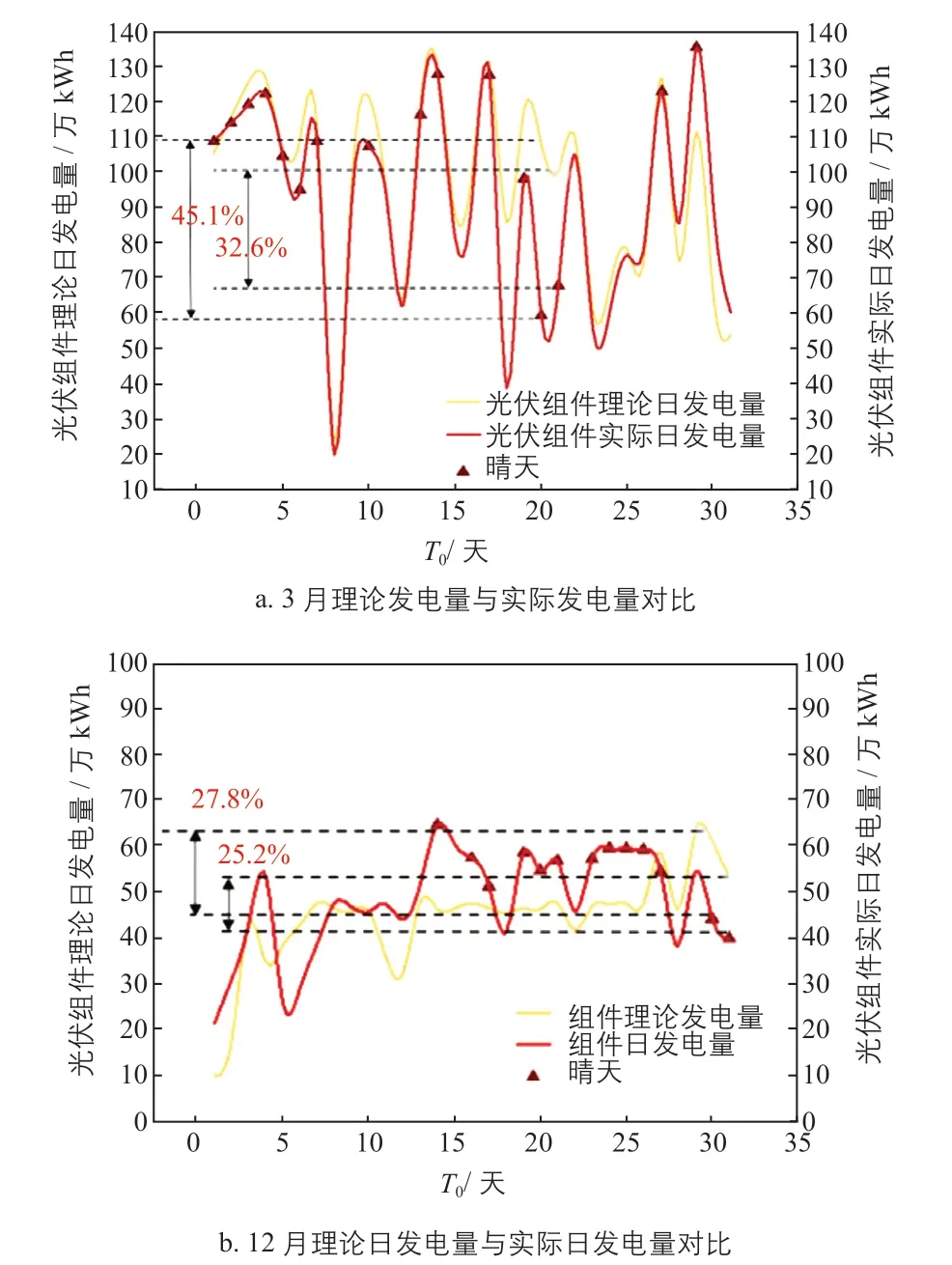
图7 3 月和12 月理论日发电量与实际日发电量对比Fig.7 Comparison between theoretical and actual daily power generation in March and December

3 月20—21 日的理论日发电量与实际日发电量的差值比例分别为45.1%、32.6%，均超过清洗经济阈值21.30%；12 月30—31 日光伏组件发电效率分别下降为27.8%、25.2%，结合气候条件发现3 月无降雨、12 月有降雪，综合考虑后认为该光伏电站3 月和12 月应开展清洗安排。

3 结论

本文引入积灰损耗系数反映因积灰导致的光伏电站发电量损失，采用K-means 算法来聚类发电日志数据得到晴天数据样本，利用样本数据拟合积灰损耗系数和发电能力损耗曲线，结合清洗成本建立了经济周期函数模型，确定了清洗经济周期和清洗阈值计算依据，得出以下结论：

1)采用K-means 算法从发电日志数据样本中提取出平均环境温度、有效发电时间、日发电量等参数数据相差不大的晴天类数据样本，由此拟合的发电量损耗曲线将更加贴近于积灰对发电量的影响。

2)引入积灰损耗系数来定量、直观地反映积灰对发电量的影响，引入清洗经济阈值结合光伏电站发电数据确定清洗周期。

3)建立了清洗策略模型，确定了具有一般性的清洗周期计算公式。

4)通过对中国西北地区某光伏电站进行算例分析，得到的清洗经济阈值通过与光伏电站长期的运行经验模型的计算结果对比，证明该模型准确性较高。